동해안 너울성 파도 예측을 위한 머신러닝 모델 연구

Ⅰ. 서 론

최근 동해안에서는 너울성 파도로 인한 인명 및 재산피해가 자주 발생하고 있다. 너울성 파도란 원해에서 바람 또는 국지성 해양현상으로 시작된 작은 파도가 다른 큰 파도와 함께 만나 진동하며 점점 세력이 커져 수심이 얕은 해안으로 밀려오는 현상을 말한다. 바람에 의한 파랑의 주기는 4~8초인 것에 반해 너울은 9~20초의 주기를 가지고 있다. 이처럼 긴 파장을 가지고 있기 때문에 육안으로 식별하기가 어려워 연안지역 인명사고의 주 원인이 된다.

너울성 파도는 항만 하역이나 선박의 계류를 방해한다. 이는 항구에 접안한 선박의 하역 중단의 주요 원인으로 작용한다. 하역 중단은 풍파, 강풍, 우천 등의 기상 악화로도 이루어지지만 너울의 발생이 주요 원인으로 지적되고 있다. 너울로 인한 하역 중단은 대부분 10월부터 2월까지 주로 겨울철에 발생한다.

과거에는 너울의 발생 원인을 분석하는 연구를 수행하기가 힘들었다. 그 이유는 파랑과 바람, 해류, 파고의 측정이 장기간에 걸쳐 이루어져야 하며, 내해에서 원해까지 광범위한 해양 환경 측정 데이터가 필요하고 다양한 기상학적 분석이 거시적으로 이루어 져야 하기 때문이다. 이러한 이유로 정온도를 유지하기 위한 방안이나 하역중단에 대한 원인을 파악하고 이를 개선하기 위한 연구가 수행되기는 했지만, 실제 관측 자료를 활용한 사례는 부족했으며 1년 이상 장기간의 데이터를 활용한 사례도 드물었다.

본 연구에서는 너울이 발생 될 때 나타나는 주요 환경 변수를 기반으로 너울의 발생 여부를 판단하는 분류 모델을 구축하고 제안한다. 분류 모델을 구축하기 위해 측정 데이터로부터 변수를 전 처리하여 새로운 변수를 생성하고, 새롭게 생성한 변수 중 너울의 발생 여부를 가장 잘 설명하는 변수 조합을 선택하기 위해 변수 선택(Variable selection) 과정을 거쳤다. 분류 모델에 사용하는 머신 러닝 알고리즘으로 Random Forest, 로지스틱 회귀(Logistic regression), KNN(k-nearest neighbor), SVM(Support Vector Machine)를 이용하여 모델을 구축하고 분류 예측 모델의 정확도를 테스트 하였다.

Ⅱ. 관련 연구

일반적으로 파고의 높이가 3m보다 높고 주기가 9초 이상인 경우 이를 너울성 파도라고 부른다[1]. 해양수산부의 해양용어 사전은 너울을 “지역적으로 멀리서 발생된 파랑이 전파되어 올 때 단주기 성분은 진행과정에서 소멸되고 장주기 성분만 포함하는 중력파”라고 정의한다[2]. 이러한 인명, 재산피해를 입히는 너울 발생의 원인을 파악하고 이를 예측하기 위한 연구가 꾸준히 진행되어 왔다.

Jung and Oh는 너울이 발생 했을 때의 동해 주변 지역의 기압배치 상황을 이용하여 너울의 발생원인을 분석한 연구를 진행하였다[3]. 너울로 인한 인명과 재산피해가 가장 빈번하게 일어나는 10월부터 2월까지의 2005년부터 2009년까지의 겨울철에 발생한 사고와 해당 기간의 기압배치 데이터를 이용하여 분석하였다. 그 결과 동해상에서 발달한 온대성 저기압과 너울의 발생 패턴이 유사함을 보였다.

파고 측정 데이터를 이용하여 푸리에 분석을 이용하여 이상고파를 분석하려는 연구도 진행되었다[3]. 동해안 일대의 5개 지점에서 발생한 이상 고파(高波)를 관측한 데이터와 바람 데이터를 활용하여 그 특성을 푸리에 분석을 적용하였다. 그 결과 너울과 같은 진행방향으로 부는 바람과, 여러 너울간의 간섭과 중첩에 의한 상승효과가 극대화 되어 발생함을 확인하였다.

반면 Kim and Lee는 웨이블릿 분석을 하여 푸리에 분석결과와 비교한 연구를 진행하였다[4]. 동해 너울의 패턴은 일시적이면서도 불규칙적인 특징에 기안한 것인데, 2008년 2월 동해의 왕돌초 파고 데이터를 이용하여 이를 웨이블릿 분석을 적용하여 푸리에 변환 스펙트럼과 그 결과를 비교하였다. 이를 통해 웨이블릿 분석을 이용하면 이상 파랑에 대한 일시적이고 불규칙적인 패턴을 분석하는데 좀더 효과적인 것을 확인하였다.

이외에도 강원도 강릉의 안목항 방파제에서 발생한 인명사고를 바탕으로 분석한 연구[5], 너울성 파도에 대한 정의와 측정기준을 정의한 김인철의 연구[6][7], 너울성 파도의 이동거리를 밀도함수를 통해 설명한 연구[8]외에 해외의 연구들이 있다[9]-[11].

Ⅲ. 예측 모델의 개발

3.1 예측변수와 설명 변수

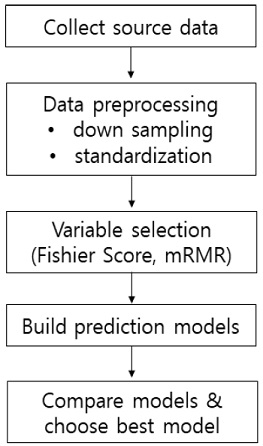
본 연구에서는 예측 모델의 개발에 있어서 그림 1 과 같이 일반적인 머신러닝 모델 개발 절차를 따랐다. 먼저 모델 개발의 기본 자료가 되는 데이터를 수집하고 모델 개발에 적합하도록 데이터를 전처리 한다. Down sampling과 데이터 표준화를 전처리 과정에서 시행한다. 그 다음으로 Fisher Score와 mRMR을 이용하여 예측에 도움이 되는 변수들을 선별 한 뒤, 다양한 머신러닝 알고리즘을 이용하여 예측모델을 수립한다. 각 예측모델의 성능을 비교하여 가장 좋은 모델을 확정한다.

Fig. 1.

Development process of prediction model

본 연구에서 개발한 예측 모델의 예측 변수는 너울의 발생 여부이다. 너울의 발생 여부는 선박의 하역중단 기록을 근거로 판단하였다. 담당자의 설명에 의하면 하역중단이 발생하는 대부분의 원인은 너울의 발생에 의한 것이고, 하역이 정상적으로 진행된 것은 너울이 발생하지 않은 것이다. 하역중단 자료는 포스코社에서 수집한 자료를 승낙을 받고 사용하였는데, 2014년 1월 4일부터 2017년 12월 27일까지 4년 동안의 기록을 포함한다. 하역이 중단된 시간대를 기록한 자료를 바탕으로 1시간 단위로 너울의 발생 여부를 예측변수로 사용하였다.

예측모델 개발을 위한 자료의 수집은 국립 해양조사원 바다누리 해양정보 서비스(htt://www.khoa.go.kr/oceangrid/khoa/intro.do)에서 제공하는 포항신항의 파랑 관측 데이터를 이용하였다. 수집한 포항 신항 항외 데이터는 조위(潮位; 조수의 흐름에 따라 변화하는 해수면의 높이), 기압, 풍속, 풍향, 수온 데이터이며 각 데이터는 자정을 기준으로 1분 간격으로 측정된다. 포항 조위관측센터의 위치는 위도 129.3838, 경도 36.04713 에 위치해 있으며 포항 신항 서북쪽에 위치해 있다. 포항 조위 관측센터에서는 영일만 부근 항외 해양 수면의 환경을 관측하기 위해 HF (High Frequency)-Radar 시스템을 이용해 영일만의 광역해수유동 정보를 측정하고 있다.

표 1은 포항신항의 파랑 관측 데이터로부터 도출한 30개 설명변수의 목록이다. 노영재, 최양호[12]의 제안에 따라 너울성 파도의 특징을 잘 설명해 줄 수 있는 새로운 변수를 추출하였다. 그 방법은 조위, 기압, 풍속, 풍향, 수온 5개 변수에 대하여 시간당 평균, 표준편차, 변동계수, 최소값, 최대값, 범위차(최대값-최소값)를 계산하는 것이다.

Table 1.

Variable lsit of wave observation

3.3 변수 선택

예측모델을 구성함에 있어서 예측에 영향을 미치는 변수들을 선별하는 과정은 매우 중요하다. 본 연구에서는 Fisher Score와 mRMR[13] 알고리즘을 이용하여 5개, 10개 15개의 변수를 선택한 모델과 전체 30개의 변수 전체를 사용한 모델의 예측 정확도를 비교하였다. Fisher Score는 변수 선택에 기본적으로 많이 사용하는 방법이고 mRMR은 변수간 유사도까지 고려하여 변수를 선택하기 때문에 비슷한 성격의 변수가 많은 본 연구의 데이터에 적합하다고 판단하여 선정하였다. 변수 선택 방법별로 선택된 변수는 표 2와 같다.

Table 2.

Result of variable selection according to variable selection algorithms (in 15 variables)

3.4 예측모델의 구축

전처리 과정을 통해 예측모델 구축에 사용한 데이터 현황은 표 3과 같다. 전체 5,356건의 데이터중 너울성 파도 발생 건수가 2,423건, 발생하지 않은 경우가 2,933건이다.

Table 3.

Dataset for building prediction model

본 연구에서는 너울성 파도를 예측하는 모델을 구축하기 위하여 일반적으로 사용하는 4개의 분류 알고리즘을 테스트 하였다. Random Forest[14], 로지스틱 회귀, KNN, SVM을 사용하여 모델을 구축한 뒤 성능을 비교하였다. 모델의 구현 및 성능평가는 Ubuntu 14.04 버전이 설치된 PC 에서 실시하였고 R 및 Rstudio IDE 환경에서 구현을 하였다. 4개의 예측 알고리즘은 모두 R 패키지에서 제공하는 함수를 이용하였으며, 모델 구축에 사용한 매개 변수는 표 4와 같다. 매개변수는 다양한 값으로 실험하여 그중 가장 좋은 성능을 나타내는 값을 선정하였다.

Table 4.

Parameter list of prediction algorithms

모델의 성능평가시 과적합 사례를 방지하기 위해 hold out 방법에 의해 데이터셋을 훈련용 데이터와 테스트용 데이터를 7:3으로 나누어 모델 구축 및 성능평가를 10회 실시하였다. 성능평가의 척도는 10회 성능평가의 평균 예측 정확도(Accuracy)를 이용하였다.

Ⅳ. 예측 모델의 성능평가

각 변수 조합 별 데이터셋에 대한 모델의 예측정확도 결과는 표 5와 같다. 6개의 모델 중 가장 우수한 예측력을 가지는 모델은 Random Forest 모델로서, 전체 30개의 모델을 사용할 때 정확도가 0.883 이었는데, Fishier Score 방법에 의해 10의 변수를 선별하였을 떄 0.8886의 최고 정확도를 보였다. 모델별로 살펴보면 KNN 알고리즘이 Fishier Score 방법에 의해 10의 변수를 선별하였을 떄 0.8444로 그 다음을 이었고 SVM이 mRMR 방법에 의해 15의 변수를 선별하였을 떄 0.8127의 성능을 보였다.

Table 5.

Accuracies of prediction models with variable selection

로지스틱 회귀분석이 가장 낮은 성능을 보였는데 mRMR 방법에 의해 15의 변수를 선별하였을 떄 0.7408의 정확도를 나타내었다. 변수 선택 알고리즘의 경우 mRMR 보다는 Fisher Score가 전반적으로 더 좋은 성능을 보이는 것을 확인하였다.

가장 높은 성능을 보인 Random Forest 모델에서 각 변수가 예측에 어느정도 기여했는지를 평가해 보았다. 대표적인 평가 방법으로 정확도 감소성(Mean decrease accuracy)와 Importance(Mean decrease gini)가 있다[15]. 정확성 감소는 해당 변수를 모델에서 제거했을 때 모델의 예측정확도가 하락함에 따라 중요도를 측정한 값이고, Importance는 해당 변수가 트리의 분할 노드를 선정함에 있어 해당 변수가 얼마나 영향을 끼치는지에 대한 측정값이다. 두 개의 평가 방법에 따르면 예측에 가장 크게 영향을 미치는 변수는 조위(TL) 이고 수온(WT)과 기압(AP)도 크게 영향을 미치는 것으로 파악되었다. 기압의 경우 Jung and Oh[16]을 뒷받침 하는 결과로 볼 수 있으나 수온은 가장 큰 영향을 끼치는 상관관계가 높은 변수임에도 불구하고 너울과의 직접적인 인과관계를 설명하기는 어렵다.

Ⅴ. 결론 및 향후 과제

본 연구에서는 동해안에서 발생하는 너울성 파도를 예측하기 위하여 너울성파도 예측에 중요한 역할을 하는 변수들을 선별 하였으며, Random Forest 예측 모델을 개발하였다. 본 연구의 결과는 너울성 파도를 미리 예측하여 항구 하역작업 중단 여부 결정에 도움을 줄 수 있을 것으로 판단된다. 선행 연구들은 저마다 다른 데이터와 방법론을 사용하였기 떄문에 본 연구결과와 직접 비교하기는 어려우나, 선행 연구와 정확도 관점에서 비교해 보면 Lee[17]에서 총 23개의 인스턴스를 사용한 신경망 모델이 65.21%의 예측정확도를 가진 반면 본 연구의 최고 모델은 예측 정확도가 88.86%인 점을 고려할 때, 기존 연구결과를 상회하는 예측 모델을 구축한 것으로 판단된다. 향후 추가적인 기상 변수 데이터가 포함된다면 예측모델의 정확도가 더 높아질 수 있을 것으로 판단된다.

본 연구의 한계는 시간의 변화에 따른 점을 반영하지 못한 점, 측정 위치를 영일만으로 한정하여 광역 측정값을 반영하지 못한 점이다. 또한 수온이 너울이 발생함에 있어서 결정적인 요인으로 작용하지만 이에 대한 관련 연구가 부족하여 기상학적인 설명을 하지 못했다는 점을 꼽을 수 있다. 또한 측정된 기상요소가 서로 영향을 주고받으면서 작용하는 변수이기 때문에 수온과 너울과의 관계에 따른 추가적인 후속 연구가 필요하다.

Acknowledgments

본 연구는 과학기술정보통신부 및 정보통신기술진흥센터의 정보통신.방송 연구개발 사업의 일환으로 수행하였음[2018-0-00242, 빅데이터 기반 인공지능 안과 진단기술 및 스마트 진료 플랫폼 개발]

References

• W. Park and W. Song, "Sustainable coastal development", Korea Institute of Ocean Science and Technology (KIOST), p. 51, 2014.
• Ministry of Oceans and Fisheries, Marine Fisheries Glossary: http://www.mof.go.kr/dictionary/list.do?menuKey=328, . [accessed: Dec. 14, 2018].
• W. Jung, S. Oh, and D. Lee, "Abonormally High Waves on the East Coast", Journal of Korean Society of Coastal and Ocean Engineers, Vol. 19, No. 4, pp. 295-302, Sep. 2007.
• T. Kim and D. Lee, "Wavelet Analysis of Swells in the East Sea", Journal of Korean Society of Coastal and Ocean Engineers, Vol. 20, No. 6, pp. 583-588, Dec. 2008.
• B. Jang, W. Yeo, J. Lee, and G. Park, "The analysis and cause tracking method for the swell-generated waves in Korea", 2008 The Korean Association of Ocean Science and Technology Societies, Jeju, Korea, pp. 2448- 2451, May 2008.
• I. C. Kim, J. Oh, and K. D. Suh, "A Proposal for Criterion of Sudden High Waves in the East Sea", Journal of Korean Society of Coastal and Ocean Engineers, Vol. 28, No. 3, pp. 117-123, Jun. 2016. [https://doi.org/10.9765/KSCOE.2016.28.3.117]
• H. S. Eum, T. S. Kang, S. Y. Nam, and W. M. Jeong, "Wave modeling considering water level changes and currents effects", Journal of Korean Society of Coastal and Ocean Engineers, Vol. 28, No. 6, pp. 383-396, Dec. 2016. [https://doi.org/10.9765/KSCOE.2016.28.6.383]
• F. Snodgrass, K. Hasselmann, G. Miller, W. H. Munk, and W. Powers, "Propagation of ocean swell across the Pacific", Phil. Trans. R. Soc. Lond. A, Vol. 259, No. 1103, pp. 431-497, May 1966. [https://doi.org/10.1098/rsta.1966.0022]
• N. F. Barber and F. Ursell, "The generation and propagation of ocean waves and swell", I. Wave periods and velocities, Phil. Trans. R. Soc. Lond. A, Vol. 240, No. 824, pp. 527-560, Feb. 1948. [https://doi.org/10.1098/rsta.1948.0005]
• M. D. Earle, K. A. Bush, and G. D. Hamilton, "High-height long-period ocean waves generated by a severe storm in the Northeast Pacific Ocean during February 1983", Journal of Physical Oceanography, Vol. 14, No. 8, pp. 1286-1299, Aug. 1984. [https://doi.org/10.1175/1520-0485(1984)014<1286:HHLPOW>2.0.CO;2]
• N. Booij, "Gravity waves on water with non-uniform depth and current", Hydraulic Engineering, pp. 23-31, May 1981.
• Y. H. Choi and Y. J. Ro, "Application of realtime monitoring of oceanic conditions in the coastal water for environmental management", Ocean Science Journal, Vol. 39, No. 2, pp. 148-154, Jun. 2004.
• B. Auffarth, M. Lopez, and J. Cerquides, "Comparison of redundancy and relevance measures for feature selection in tissue classification of CT images", Advances in Data Mining. Applications and Theoretical Aspects. pp. 248-262. Jul. 2010. [https://doi.org/10.1007/978-3-642-14400-4_20]
• S. Raschka, "Python machine learning", Packt Publishing Ltd, Sep. 2015.
• M. Seo, "Data processing & analysis using R", Gilbut, Oct. 2014.
• W. Jung and S. Oh, "Abnormally High Swells Occurred on the East Coast in Recent Several Years", 2009 The Korean Association of Ocean Science and Technology Societies, Changwon, Korea, pp. 2119-2122, May 2009.
• J. Lee, K. Ryu, W. Baek, and W. Jung, "Wave Height and Downtime Event Forecasting in Harbour with Complex Topography Using Auto-Regressive and Artificial Neural Networks Models", Journal of Korean Society of Coastal and Ocean Engineers, Vol. 29, No. 4, pp. 180-188, Aug. 2017. [https://doi.org/10.9765/KSCOE.2017.29.4.180]