숫자 인식 서비스 기반 다층 퍼셉트론에 대한 입력 데이터 축소 알고리즘

2.1 ANNs

ANNs(Artificial Neural Networks)의 기본적인 구조는 생물학적 뉴럴 네트워크(BNN, Biological Neural Networks)를 기반한다[3][4]. BNN은 뉴런이라는 하나의 세포가 약 103~104의 다른 뉴런들과 상호 연결된 네트워크로 구성된 형태(인간의 뇌는 약 1,014~1,015개의 상호 연결됨)로, 밀리초 단위의 시간에 신호를 통신한다. 이러한 생물학적 뉴런을 McCulloch와 Pitts는 이진 원소로 판단하여 “A Logical Calculus of Ideas Immanent in Nervous Activity”을 통해 McCulloch-Pitts 모델을 제안하였다.

그림 1은 인공 뉴런을 표현한 것으로, 합계 연산 부분과 임계값 비교를 위한 부분인 활성화 함수(Activation function)로 구성된다. 합계 연산은 입력과 각기 다른 가중치를 곱한 후 합산을 구하는 부분이며, 활성화 함수는 합계와 임계치를 비교하여 활성상태(0, 1)를 판단한다. 활성화 함수는 계단함수(Limiting), 임계 논리(Threshold logical) 등 다양한 함수가 존재한다. 하지만 이 모델은 불완전하며 연산의 모호함으로 인해 뇌 활동에 대한 정확한 모델링이 아닌 것으로 판명되었지만 오늘날의 인공신경망에 표본이 되었다.

Fig. 1.

Artificial neuron

2.2 다층 퍼셉트론 및 역전파 학습알고리즘

McCulloch-Pitts 모델 이후 프랭크 로젠블럿(Frank rosenblatt)에 의해 등장한 퍼셉트론(Perceptron)은 비교적 정확히 기술된 계산에 의해 최초의 신경망 모델이 되었다. 그는 인공 뉴런의 개념을 이용하여 단층 퍼셉트론을 제안하였지만 선형 분리의 문제를 해결하지 못했다. 이후 입·출력층 이외의 은닉층(Hidden layer)을 추가한 다층 퍼셉트론(MLP, Multi-Layer Perceptron) 모델이 탄생되었으며, 오류 역전파 학습 알고리즘(Back-propagation)의 등장으로 단층 퍼셉트론의 문제 및 다양한 이슈를 해결하였다[4]-[7].

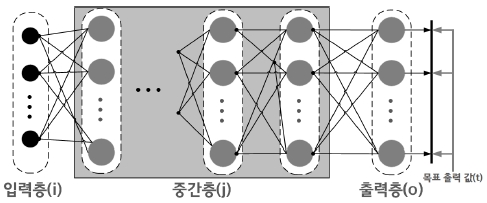
그림 2는 MLP의 구조로, 각 계층 내 다수의 노드가 존재하며 각 노드는 인접된 계층의 모든 노드와 완전연결 구조를 형성한다. 입력층을 제외한 모든 계층은 이전 계층에서 도출된 결과를 입력으로 받으며, 각 노드는 일련의 연산과정(합계와 활성화 함수)을 수행 후 다음 계층으로 상태를 전달한다. 일반적으로 다층 퍼셉트론은 시그모이드 함수를 사용하며, 3계층으로 설계된다. 식 (1)은 시그모이드 함수이다.

Fig. 2.

Multi-layer perceptron

식 (1)의 x는 입력 값이며, 지수함수를 통해 x에 대한 0~1사이의 미분 가능한 수로 변환되어 시그모이드 그래프를 표현한다. 이 그래프는 S자와 유사한 시그모이드 커브 형태를 보인다. 이를 통해 각 노드는 활성화 상태를 1 또는 0으로 표현한다.

MLP은 일련의 신호를 입력층부터 각 계층을 순차적으로 처리하는 순방향 연산(Forward-propagate)을 수행한다. 이 과정에서 가중치(Weight) 및 바이어스(Bias)를 변화시킨다. 이는 주어진 노드들을 이용하여 목적 패턴을 분류할 수 있는 가중치 및 바이어스를 찾아내는 작업으로, 일반적인 신경망은 각 노드의 가중치들을 조정하기 위해 식 (2)와 같은 경사하강법(Gradient descent)을 이용한다.

식 (2)의 θ는 파라미터(가중치), α는 학습률(Learning rate), (∂/∂θ_j)×J(θ)은 미분 값을 의미한다. 즉, 학습 신경망은 가중치 조정으로 미분 값을 사용하며, 이 미분 값 계산을 위해 오류 역전파 알고리즘을 사용한다.

그림 3은 오류 역전파 알고리즘에 대한 수행과정을 도식화한 내용이다. 순방향 연산을 통해 도출된 a³을 실제 값 y와 비교하여 오차 δ³을 산출한다. 오류 역전파 알고리즘은 산출된 δ³을 이전 계층의 각 노드에게 역으로 전파한다. 이전 계층은 식 (2)의 미분 값을 해당 층에서 도출된 a^l과 역전파 δ^l+1을 통해 해당 층의 오차를 계산한다. 즉, 식 (2)의 미분 값은 해당 층의 산출 결과와 역전파 받는 오차로 대체되어 각 노드의 가중치를 조정한다. 오차는 평균 제곱 오차(MSE, Mean Squared Error) 손실 함수를 사용하여 출력 값과 실제 값의 오차를 제곱 후 더하여 계산된다. 이를 통해 산출된 값이 최소인 모델을 제작한다. 하지만 이 함수의 값이 0으로 측정되는 것은 어려운 일로, 반복적인 작업을 요한다. 그로 인해 반복 횟수가 기하급수적으로 증가한다. 그래서 MSE 함수의 값을 측정할 때 임계값 또는 최대 반복 횟수를 지정하여 학습을 수행하다.

Fig. 3.

Process of back-propagation algorithm

2.3 데이터 축소를 위한 특징선택 및 특징추출

데이터 축소 기법(차원축소)을 통해 원본 데이터의 크기 감소 및 분류 성능 향상을 목표로 한다. 이를 수행하는 기법으로 특징선택(FS, Feature Selection)과 특징추출(FE, Feature Extraction)이 대표적이다[8][9]. FS은 모든 특징의 부분 집합을 선택하여 간결한 특징 집합을 만드는 것을 목적으로, 분류 정확도를 향상시키기 위해 원본 데이터 내 성능을 높일 수 있는 데이터의 부분 집합(Subset)을 찾아내는 방법이다. 즉, 분류기의 분류 목적에 가장 밀접하게 연관된 특징들만을 추출하여 새로운 데이터를 만든다. FS의 수행과정은 특징 부분 집합 생성, 평가, 정지조건 만족여부로 구분된다. 원본 데이터 내의 부분집합을 추출 후 평가하여 우수성을 측정한다. 측정 결과가 정지조건을 만족할 때까지 이 과정을 반복 수행한다. 조건을 만족하는 부분집합들을 이용하여 분류기의 학습 데이터로 사용한다. FS은 부분집합을 생성할 때마다 평가 작업으로 인하여 수행시간이 길다. FE은 원본 데이터 내의 주축을 찾고, 모든 데이터를 해당 축에 투영시킨다[9][10]. 일부 중요 특징을 부분집합으로 빼내는 FS와는 대비된 기법이다. FE을 수행하기 위해 주성분분석(PCA, Principal Component Analysis)를 주로 이용한다. PCA의 핵심 아이디어는 데이터의 분산(Variance)이 가장 큰 방향으로 정사영 시킨다. 즉, PCA는 가장 큰 특징(핵심 특징)들을 추출하는 방식으로 데이터를 축소시키는 방법이다. 두 기법들은 공통적으로 데이터를 축소시키기 위해 모든 특징 중 부분선별 또는 핵심 특징을 추출하고 나머지를 제거시킨다. 하지만 본 논문이 제안하는 데이터(차원) 축소 방식은 윤곽선 작업을 통해 찾을 수 있는 모든 특징을 일련의 패턴으로 함축시키는 방식을 보인다. 즉, 특징을 정리하여 분류하는 방식이다.

3.1 학습 데이터의 축소

ANN 모델의 학습 데이터를 고정적 크기로 변경하는 일련의 과정을 제안한다. 사용한 데이터는 0~9까지의 이미지이며 크기는 28×28이다. 이 이미지들을 1×16 크기로 축소시킨다. 이 데이터들은 1채널로 표현되며, 3 단계로 축소 작업이 수행된다.

3.1.1 윤곽선 검출

로드된 이미지들은 윤곽선 검출 알고리즘을 통해 윤곽선 데이터로 변환한다. 윤곽선 검출 알고리즘은 식 (3)과 같다. 식 (3)의 x은 원본 이미지를 의미하며, x¹, x²은 원본 이미지를 이용하여 파생된 중간 이미지맵이다. I와 J는 원본 이미지의 크기, m을 median() 함수, n¹, n²은 중간 이미지를 생성 시 사용할 필터의 크기이다.

(3)

식 3(A)는 원본 이미지에 필터 영역을 적용하여 포함된 영역의 값을 m을 통해 중간 값을 산출한다. 이 중간 값은 다음 필터 영역에서 계산된 값과 빼기 연산을 수행 후 절댓값으로 표현된다. 필터 영역이 가로 또는 세로 방향으로 이동함에 따라 x¹, x²가 각각 정의된다. 식 3(B)는 x¹와 x²을 합칠 때 사용될 임계값 δ을 구하는 과정이다. 식 3(C)의 x_edge는 x¹와 x²의 평균계산 후 δ을 기준으로 1 또는 0으로 결과를 나타내며 그림 4와 같다.

Fig. 4.

Outline detection result image

3.1.2 이미지 분할

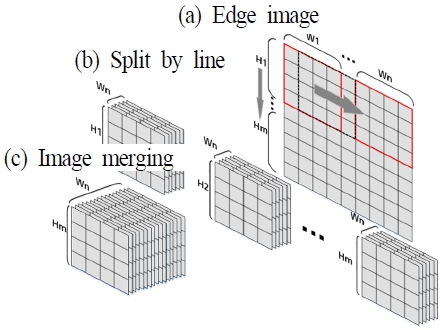
입력 이미지에 대한 윤곽선 검출은 그림 4와 같은 형식이며, 이러한 이미지를 8×8 크기로 분할한다. 이때 분할된 이미지들은 일정 영역이 겹쳐진 상태로 이미지들이 분할된다. 그림 5는 윤곽선 이미지를 8×8 크기로 분할하는 과정으로 그림 5(a)와 같이 윤곽선 이미지를 8×8크기로 분할하면서 한 칸씩 이동(stride=1)하여 전체를 스캔한다. 그림 5(b)는 각 라인별 분할된 데이터이며, 5(c)는 분할된 이미지를 합친 행렬이다.

Fig. 5.

Image split and merge process

3.1.3 이미지 축소 작업 및 형식 변환

위절에서 설명한 작업은 이미지를 간소화하기 위한 준비과정으로, 본 절에서는 간소화 작업 및 형식 변환을 수행한다. 그림 6은 이미지 간소화 작업에 대한 처리 과정으로 6(a)는 8×8 데이터를 4×4 필터로 스캔한다. 이때 필터의 이동 간격은 2(stride=2)로, 8×8 데이터를 4번 이동하여 특징맵을 생성한다.

Fig. 6.

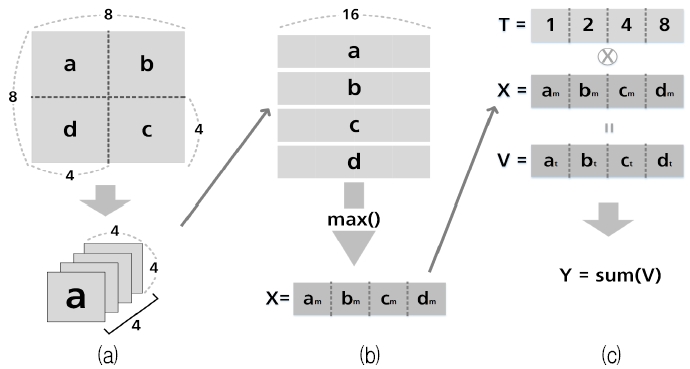
Image streamline operations and transformation, (a) Image division, (b) Calculate the max value of each area, (c) Specify mappings and thresholds

4등분된 특징맵은 각 영역에 배치 값을 선정하여 배치 순서에 맞게 특징맵을 정렬 후 그림 6(b)와 같이 각 특정 맵의 최댓값을 검출하여 행렬 x를 생성한다. x는 윤곽선 검출 작업으로 인하여 1 또는 0의 값을 지니고 있어 4비트의 2진수와 유사하다. 이러한 x에 T[1, 2, 4, 8]을 곱하여 10진수 형태의 데이터로 변환 후 합산하여 Y를 산출한다. 산출된 Y는 표 1을 통해 분류한다.

Table 1.

Type of line for active area

그림 6의 x는 2진수와 같은 형식으로 표현되며, 2진수를 표 1과 같이 선의 종류로 구분한다. 구분된 선은 10진수의 값을 인덱스(index) 값으로 표시하여 16크기의 배열을 구성한다. 즉, 이미지의 크기와 상관없이 0~15 범위 사이의 값으로 표현시킬 수 있다. 이러한 분류 과정을 통해 산출된 데이터는 그림 7과 같다.

Fig. 7.

Graph for the sorted segment

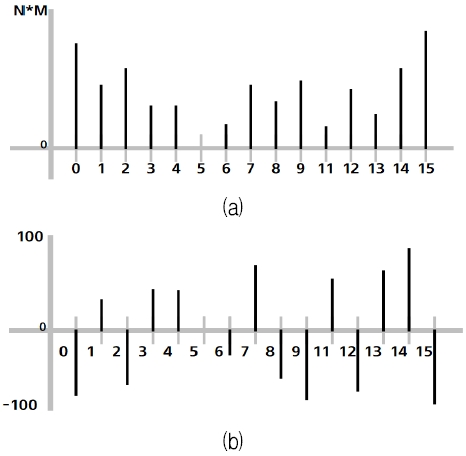
그림 7은 y 축의 N*M은 이미지의 너비와 높이의 곱을 나타내며, x축은 인덱스를 의미한다. 그림 7(a)는 그림 6의 Y 값을 분류하여 산출된 그래프이며, 그림 7(b)는 그림 6(b)의 X 평균을 구하여 0.5 미만인 경우 –1을 곱하여 음의 영역을 표현한 것으로, 데이터의 특징을 극대화한다.

위와 같은 처리 과정을 통해 학습 데이터의 크기를 1차원 형식으로 변경시킨 후 ANN 모델을 설계하여 학습한다.

3.2 축소 데이터 학습을 위한 ANN모델 설계

본 절은 위에서 설명한 과정으로 축소된 데이터를 학습하기 위해 설계된 학습 신경모델에 대한 내용이다. 그림 8은 설계한 학습 신경모델이다.

Fig. 8.

Proposed learning model

그림 8은 본 논문이 제안한 축소된 데이터를 학습하기 위한 신경모델이다. 입력층과 하나의 은닉층, 출력층으로 기존의 3층 구조를 따른다. 활성화 함수는 relu() 함수와 sigmoid() 함수를 사용한다. 이는 relu() 함수를 통해 데이터들의 차이를 명확하게 구분하고 sigmoid() 함수로 부각된 특징들을 세밀하게 분류한다. 이를 통해 산출된 값은 softmax() 함수를 통해 결과 Y가 생성된다. 본 모델은 오류 역전파 알고리즘을 적용하여 결과 Y에 대한 오차율이 0.02% 미만으로 측정될 때까지 반복한다.

4.1 학습시간 및 오차율 측정 실험

학습시간 및 오차율을 측정하기 위해 20회 당 1세트로 구성하여, 총 5세트를 수행 후 본 실험의 데이터를 측정하였다.

표 4는 오차율 측정 테이블로 제안한 알고리즘(PreAlgo)은 약 0.026이며, 3계층-ANN은 약 0.019, CNN-LeNet5은 약 0.018를 보인다. 이 실험 결과를 고찰할 시 PreAlgo은 약 1.5배 정도의 다소 저조한 차이를 보인다. 하지만 본 논문의 실험 목표 및 축소된 데이터 활용 사항을 고려할 경우 이 정도의 차이는 감안 가능한 사항으로 판단된다. PreAlgo은 배열 16 크기를 이용하여 한 이미지 내에 존재하는 모든 특징을 특징별로 정리되어 이루어진 집합데이터이다. 이를 다시 말하면 특징들의 분류 작업 시 밀집된 특징(특징-몰림 현상)들 사이에 경계선을 그려야하는 의미가 된다. 그러므로 기존방식과 다르게 적은 특징들의 조합으로 학습을 수행할 때 발생되는 차이와 축소과정에서 특징의 일부 손상 또는 제거로 발생되는 현상으로 오차율이 증가되는 것으로 판단된다.

Table 4.

Error rate measurement table

표 5는 학습시간을 측정한 데이터를 보인다. 본 데이터들을 고찰할 경우 PreAlgo은 0.04초, ANN은 0.13초, CNN은 4.53초로, PreAlgo가 약 3배 이상 빠른 연산을 보인다. 이는 학습 데이터의 크기를 16배열로 변환하여 기존 모델들 보다 연산속도 및 연산량이 적어 학습이 빠르게 진행된다. 결론적으로 본 알고리즘은 다른 모델들 보다 다소 저조한 오차율을 보이는데 반해 학습시간 및 연산에 있어 다른 모델들보다 높은 성능을 보인다.

Table 5.

Learning time measurement table

4.2 정확도 측정 실험

본 실험은 각 모델을 학습 후 테스트 데이터를 이용하여 정확도를 측정한다. 표 6은 정확도를 측정한 데이터이다.

Table 6.

Accuracy measurement table

표 6을 고찰할 경우 3계층-ANN(0.997)이 가장 높으며 CNN-LeNet5(0.995), PreAlgo(0.994) 순을 확인할 수 있다. 모든 모델이 약 99%의 정확도를 보이나, 본 논문이 제안하는 알고리즘이 가장 낮은 결과를 나타내고 있다. 본 저자는 이를 오차율 측정 실험 때와 같이 “특징-몰림 현상”으로 인하여 “특징-결합 현상”이 발생된 것으로 판단하고 있다. 본 논문이 제안한 데이터 축소 알고리즘은 표 1(3.1.3절)을 통해 이미지 내의 존재하는 특징들을 파악 후 정리하여 단일 배열(16크기)로 변환한다. 이를 다시 표현한다면 일반적인 이미지가 표현할 수 있는 특징의 범위를 감소(다양한 특징이 16가지의 종류로 몰림)시킨 것이다. 즉, “특징-몰림 현상”으로 인하여 일부 서로 다른 특징들이 결합(인접)되는 현상이 발생된 것으로 판단하고 있다. 이 현상으로 인하여 정확도가 낮아지는 것으로 분석하고 있다.

4.3 실험결과 및 기대효과

본 논문은 학습 신경망의 입력 데이터를 줄일 수 있도록 데이터 축소 알고리즘을 제안한다. 이는 딥러닝의 고질적 문제인 고연산량을 다소 줄이기 위해 고안되었다. 축소 알고리즘을 통해 가공된 배열 16크기의 데이터를 학습 신경망의 입력으로 활용하여 학습된 결과와 기존방식으로 학습이 이루어져 도출된 결과를 비교할 시 PreAlgo은 정확도 및 오차율이 기존방식으로 처리된 결과보다 다소 저조한 결과를 보인다. 하지만 이러한 결과는 학습 데이터의 특징 감소로 발생되는 “특징-몰림” 및 “특징-결합” 현상으로 파악된다. 특징-몰림은 복잡한 특징들이 단순한 특징 패턴으로 변화되는 과정으로 인하여 특징 표현범위가 밀집되는 형태를 의미하며, 특징-결합은 특징 표현범위가 밀집됨에 따라 유사한 특징들이 서로 달라붙는 현상을 의미한다. 하지만 특징-몰림 및 특징-결합은 본 저자의 가설로 이 현상들이 아닌 다른 원인으로 오차율 및 정확도가 떨어질 수 있다. 이 현상들을 증명하기 위한 추가적인 연구 및 실험을 진행하고 있다.

본 논문이 제안한 숫자 데이터 축소 알고리즘이 더욱 발전되어 숫자만이 아닌 문자, 필기체 등 다양한 데이터에 따른 성능이 안전적으로 평가된다면 우리는 딥러닝의 고연산량을 다소 감소시킬 수 있다. 또한 본 알고리즘을 모바일 및 소형 단말기 기반 패턴 인식서비스 시스템에 접목한다면 전송되는 데이터 형식을 이미지 압축 기법이 아닌 단순 문자열(배열 16크기의 특징-집합데이터)로 대처할 수 있으며, 전송 데이터양을 줄여 보다 많은 양을 한 번에 묶어 전달할 수 있게 된다. 이러한 데이터를 전송받은 서버 및 PC는 인식서비스로 인한 시스템 부하를 줄일 수 있으며, 하드웨어 자원이 다소 낮을 경우라도 원활한 서비스 제공이 가능해 진다. 또한 점차 깊어지는 모델들을 보다 적은 레이어로 대체 가능할 수 있다고 판단한다.