실제 상황을 고려한 MoM/UTD 혼합 전자파 수치 해석 알고리즘 내장 고해상도 방향 탐지 시뮬레이터 개발 및 응용
 ; Seung-Gyu Yang**
; Seung-Gyu Yang** ; Ill-Keun Rhee***
; Ill-Keun Rhee*** ; Joong-Soo Lim****
; Joong-Soo Lim**** ; Young-Ho Kim****
; Young-Ho Kim**** ; Myung-Ho Chae*****
; Myung-Ho Chae*****
초록
본 논문에서는 항공기에 설치된 방향 탐지(이하 ‘방탐’) 안테나로부터 얻어진 지상 목표물로 부터의 신호와 안테나 주변 잡음이 혼재된 데이터를 이용하여 목표물의 방탐을 수행하기 위한 최적의 안테나 개수 및 안테나 배열 예측 등 실제 방탐시스템 운용 및 설계를 염두에 두고 다중 안테나 어레이 기반 고해상도 방탐 기법들의 활용을 위한 통합 시뮬레이터를 개발하였다. 먼저 실제 환경에서 존재하는 안테나 플랫폼 주변의 난반사 등을 고려한 MoM/UTD 전자파 수치해석 관련 이론과 이를 이용하여 생성된 신호들과 고해상도 안테나 어레이 방탐기법들을 통합하여 개발된 시뮬레이터의 구성에 관해 기술한 후, 본 시뮬레이터를 이용하여 여러 가지 상황 하에서 방탐 수행 및 본 시스템 응용을 위한 방안들을 살펴봄으로써 본 시뮬레이터의 활용도를 입증하였다.
Abstract
In this paper, we proposed an integrated DF(direction finding) simulator with well-known high resolution DOA estimators with MoM/UTD numerical analysis technology using the ground signal data obtained from antenna array added with the diffused reflection caused by structural characteristic of aircraft platform mounting antenna array, for real fire DF system design in terms of the parameters such as the optimal number, etc, in mind. We also demonstrated the feasibility of this simulator by investigating application plans in various situations.
Keywords:
DOA, MUSIC based algorithms, correlative interferometer, MoM/UTDⅠ. 서 론
목표물의 도래방향각(Direction-of-Arrival: DOA)을 탐지하는 방향 탐지(Direction Finding: DF)는 전자전(Electronic Warfare: EW) 또는 어군 탐지와 같은 다양한 분야에서 활용되고 있다. 이러한 방탐를 위해, 안테나가 배치된 항공기와 같이 기동성이 있는 플랫폼은 목표물에 대한 정보를 효율적으로 수집할 수 있다[1][2]. 이들 플랫폼에는 단일 안테나 또는 다중 안테나가 배치될 수 있다. 다중 안테나가 배치될 경우가 단일 안테나가 배치되는 경우에 비해 신호 대 잡음비(Signal-to-Noise: SNR)가 상대적으로 높을 수 있다[1][2].
한편 다중 안테나 어레이 주변에 잡음이 존재하는 상황에서 목표물로부터 플랫폼에 수신된 신호 샘플들로부터 얻어진 공분산 행렬을 이용한 고유구조(Eigen-structure)기반의 고해상도 DOA 예측기법들에 대한 연구와 함께 다중 안테나 사이의 위상차를 비교하여 DOA 예측을 수행하는 인터페로메터 및 상관형 위상비교 방법 등의 연구들이 활발히 진행되고 있다[3]-[7]. 이러한 고해상도 방탐 알고리즘들을 실제 항공기에 탑재하여 방탐 임무를 성공적으로 수행하기 위해서는, 신호정보(Signals intelligence: SIGINT)시스템에 의해 얻어지는 목표물로부터 발생되는 신호 주파수 등의 파라미터 정보뿐만 아니라 사용되는 방탐 기법들을 최적으로 활용할 수 있는 신호 및 잡음 환경에 적합한 항공기에 장착되는 안테나 개수 및 안테나 배열 등에 대한 설계가 매우 중요하다. 따라서 실제 환경과 유사한 환경 하에서 필요로 하는 항공기에 설치되는 최적의 안테나 개수 및 안테나 배열을 미리 예측해 낼 수 있는 효율적인 시뮬레이터를 개발하여 최적의 방탐 알고리즘 도출을 위해 사용한다면, 막대한 시간 및 비용 절감뿐만 아니라 실패 위험 부담도 현저히 감소시킬 수 있을 것이다.
실제와 유사한 환경 하에서의 방탐 수행을 위해서는, 안테나에서 수신된 신호에 대한 전자파 수치 해석 과정이 포함될 수 있다. 이러한 전자파 수치 해석 과정에는 전술한 플랫폼의 영향이 고려될 수 있어야 한다. 왜냐하면 안테나에서 수신된 신호에는 목표물에서 반사된 신호 뿐 아니라 플랫폼에서 반사된 신호 등이 함께 수신될 수 있는데, 이렇게 플랫폼에서 반사된 신호는 목표물에서 반사된 신호와 상호 간섭을 일으킴으로써 방향 탐지에 유의미한 영향을 끼칠 수 있기 때문이다.
본 논문에서는 항공기에 설치된 방탐 안테나로부터 얻어진 지상 목표물로 부터의 신호와 안테나 주변 잡음이 혼재된 데이터를 이용하여 목표물의 방탐을 수행하기 위한 최적의 안테나 개수, 안테나 배열 예측 및 고해상도 방탐 기법 활용을 위한 통합 시뮬레이터를 개발하였다.
여기서는 먼저 개발된 시뮬레이터의 구성 및 관련이론을 기술한 후, 본 시뮬레이터를 활용하여 여러 가지 상황 하에서 방탐 수행 및 본 시스템 응용을 위한 방안들을 논의한 다음 결론을 맺는다.
Ⅱ. 개발된 시뮬레이터 구성 및 관련이론
실제 항공기를 활용한 목표물 방탐과 유사한 환경 하에서 동작하는 시뮬레이터를 개발하기 위하여 플랫폼 구조물에 장착된 안테나 주변에서 감지되는 신호 및 잡음 모델을 실제 항공기 구조물의 크기, 형태, 특성, 그리고 난반사 등을 고려한 안테나의 특성들을 반영한 해석이 가능하도록 구성하였다.
전함이나 전투기 등과 같이 주파수 대비하여 크기가 큰 플랫폼에 부착된 안테나를 효과적으로 해석하기 위해서는 이에 적합한 전자파 수치해석 방법이 요구된다. MoM(Method-of-Moments)은 안테나의 특성을 해석하기 용이하나 구조물의 크기에 제약이 많으며, UTD(Uniform-Theory-of-Diffraction)은 큰 구조물에 적합하지만 안테나의 특성을 해석하는데 어려움이 많다[8][9].
표 1에서는 해석 구조물의 크기에 따른 대표적인 전자파 수치해석 알고리즘 별 컴퓨팅 속도를 표현하였다[11]. 풀 웨이브 방법으로 불리는 MoM, FEM, FDTD는 높은 정확도를 가지나 구조의 크기에 따른 제약이 따른다. 그 중 비교적 FDTD 방식이 큰 구조에 적합한 것으로 보이나, 전투기 등의 플랫폼에서는 이 방법 또한 적용이 어렵다. 따라서 GO, PO, UTD 등과 같은 점근적 방법들이 고려되어져야한다.
따라서 플랫폼에 부착된 레이더들을 활용한 방탐을 수치적으로 해석하기 위하여 MoM/UTD 혼합 방법이 고려되어 질 수 있다. 본 연구에서는 플랫폼 영향을 해석하기 위한 UTD와 안테나 해석을 위한 MoM을 서로 혼합한 방법을 개발하였다.
다수의 전자파 수치해석 방법이 혼합된 경우, 수치해석 방법 간의 경계 설정에 어려움이 따른다. 기존의 MoM/UTD 혼합 방법은 안테나 및 인근영역은 MoM으로 해석하고 이외 영역에 대한 효과는 UTD를 활용하는 방법으로 사용되어 진다[10][11]. 안테나 인근영역의 크기 즉 MoM 영역이 너무 작은 경우 해석결과의 정확도가 낮은 특성을 보이며, 해당 영역의 크기가 일정 수준이상 커진 경우 정확도가 수렴하는 현상이 일어난다. 다만 MoM 영역의 크기가 상승함에 따라 높은 컴퓨팅 파워를 요구하기 때문에 적절한 경계 설정이 필요하다.
MoM은 주파수영역에서 면 또는 체적 적분 방정식을 푸는 방법으로, 벡터포텐셜을 이용하여 방사되는 필드를 계산한다[12][13]. 3차원 그린함수를 이용할 때 벡터포텐셜에 의해 생성되는 전자계는 다음과 같다.
| (1) |
| (2) |
| (3) |
| (4) |
위 수식들에서 전계 및 자계는 등방성 유전체 영역(Homogeneous dielectric region)를 가정했을 때 방사되어지는 필드의 표현으로써, G(r,r′)는 자유공간에 대한 3차원 그린 함수이다. 서로 다른 매질이 경계를 형성할 경우에 대한 문제를 해결하기 위해, 일반적으로 EFIE(Electric-Field-Integral-Equation)가 활용되어 지며 이는 식 (5)와 같이 표현가능하다.
| (5) |
MoM에서는 Galerkin-type testing을 통해 EFIE을 행렬 시스템으로 변환하는 과정이며, 전류와 자류를 가중기저함수(Weighted-basis-function)들의 합들로 표현할 경우 EFIE는 식 (6)~(10)들과 같이 표현할 수 있다. MoM의 경우 기저함수가 그린함수를 통하여 다른 요소들과 상호작용 하기 때문에 Full Matrix형태를 가지게 된다.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
본 연구에서는 MoM 영역의 크기를 작게 설정하면서 비교적 높은 정확도를 가지기 위한 방법으로 다음을 제안한다. 플랫폼에 부착된 안테나 부분만을 MoM 영역으로 설정하고 인근 영역에 대한 현상을 그린함수를 이용하여 해석한다. 일반적으로 MoM 알고리즘에서는 임피던스 매트릭스를 사용하는데, 임피던스 매트릭스를 계산하는데 있어서 자유공간에서의 전자파 진행을 가정한 그린함수를 사용한다. 안테나 인근에 무한한 평판이 존재할 경우, 무한 평판을 고려한 그린함수를 사용한다.
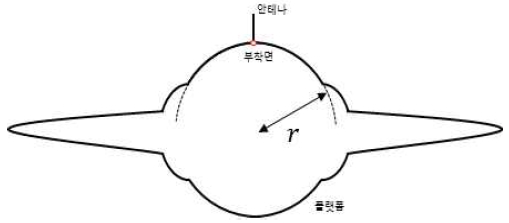
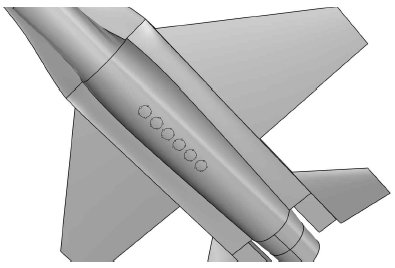
그림 1은 간단하게 묘사된 비행기 모양의 플랫폼에 안테나가 부착된 그림이다. 안테나가 플랫폼에 부착된 지점을 빨간색 원으로 표현하였으며, 빨간색 원에서 플랫폼의 주곡률 반경을 r로 표현하였다.
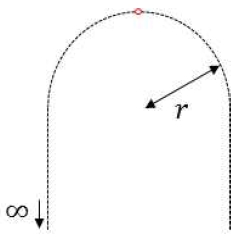
그림 2와 같이 안테나가 부착된 플랫폼 지점의 주곡률을 이용하여 반구 혹은 반원을 가정하고 아래로 무한히 긴 평판으로 구성된 상황에서 사용될 수 있는 그린함수를 계산하여 임피던스 매트릭스에 반영한다. 이 경우 안테나 인근 영역을 모두 고려하여 MoM으로 해석하는 경우에 비하여 연산량이 매우 크게 줄어들 수 있어 계산 속도를 높이고, 요구되는 메모리양을 줄일 수 있다.
그림 1 상황을 MoM 방식으로 해석할 수 없다고 가정하였을 때, 안테나를 특성을 해석하기 위한 방안으로 평평한 무한 평면위의 안테나가 고려하여 질 수 있다. 무한 평면을 가정하고 해석한 경우, 매우 높은 주파수에서는 정확한 특성을 보일 수 있으나 주파수가 낮아질수록 정확도가 떨어지는 경향을 가지게 된다. 본 논문에서 제안한 방식을 사용할 경우와 무한 평판으로 가정한 경우, 두 경우 모두 MoM 미지수의 개수가 같다. 따라서 두 방식 간 속도 방면에서 차이가 적으나 제안한 방식은 비교적 정확한 특성을 얻을 수 있다.
해석 대상의 크기가 파장대비 상대적으로 클 경우 GO(Geometrical-Optics), PO(Physical-Optics), UTD 등과 같은 점근적 알고리즘이 사용된다. UTD는 회절현상을 표현하지 못하는 GO를 개선한 방법으로, 페르마의 원리를 만족하는 파선들을 고려하여 플랫폼의 효과를 적용한다[9]. UTD에서 고려되는 파선으로 식 (11)~(14)들로 표현되는 직접, 반사, 쐐기회절, 표면회절 파선들이 주로 사용된다.
| (11) |
| (12) |
| (13) |
| (14) |
대형 플랫폼에 안테나가 부착된 경우 MoM/UTD 혼합방법을 사용할 수 있다. 안테나를 플랫폼이 없는 가상의 환경이나 무한평판을 가정하여 MoM을 통해 안테나의 전류를 계산한 후, 계산되어진 전류를 UTD를 활용하여 플랫폼에 대한 영향을 반영한다. 플랫폼에 대한 영향은 MoM에서 사용되는 임피던스 행렬의 형태로 변환하여 플랫폼에 의한 영향이 고려된 안테나 전류가 계산가능하다.
본 연구에서는 혼합방법에 사용되어지는 MoM의 임피던스 행렬 [Z]는 앞서 제시한 그린함수 계산법을 통해 얻어진다. 적은 MoM 미지수에 따른 높은 계산 속도와 비교적 높은 정확도를 가지는 특성은 혼합방법에서도 고스란히 영향을 끼친다. UTD에서 MoM 미지수는 신호원으로 고려되어 진다. 따라서 UTD 계산량은 MoM 미지수의 개수에 직접적인 영향이 있기 때문에 적은 미지수가 혼합방법에서 큰 장점이 된다. 이후 UTD로 계산되어진 플랫폼 및 안테나 간의 상호간섭 [∆Z]로 표현한다. 즉,
| (15) |
| (16) |
식 (15)로 표현되는 수정된 임피던스 행렬 [Z′]을 이용하여 안테나의 최종 전류는 식 (17)과 같이 얻을 수 있다.
| (17) |
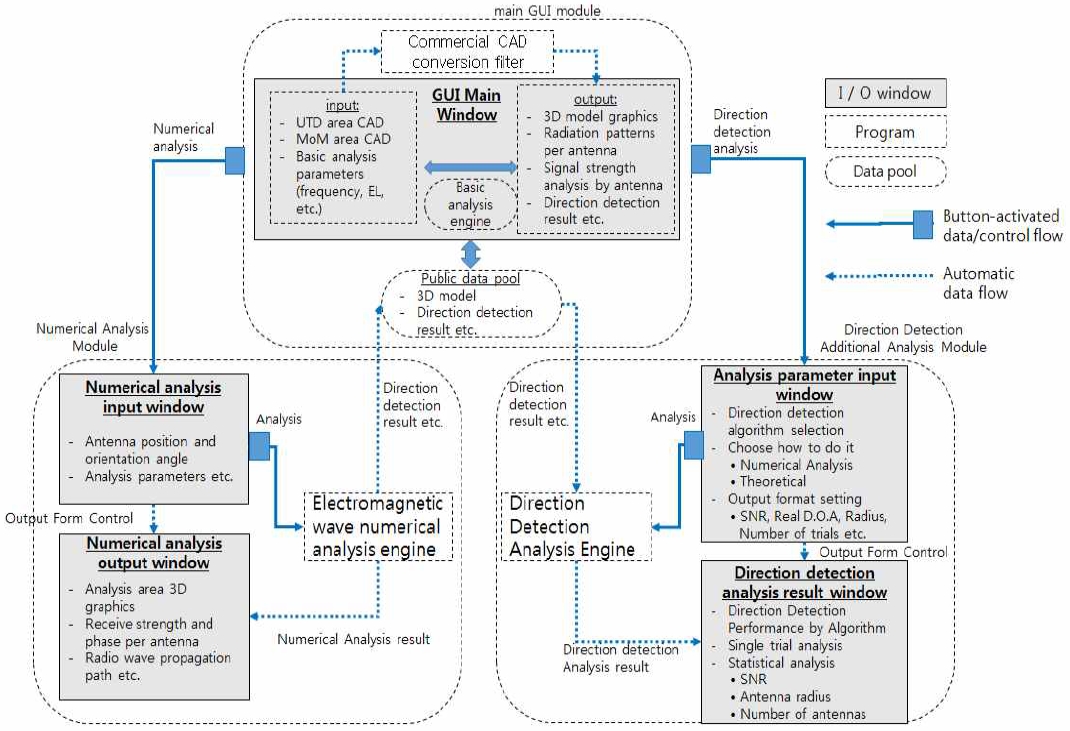
위에 설명된 내용은 개발된 그림 3의 통합 시뮬레이터의 전자파 해석 모듈 부분 내에서 플랫폼 및 안테나 간의 상호간섭이 고려되어 플랫폼에 장착된 안테나에서 얻어지는 신호를 생성해 내는 원리에 대한 것이다.
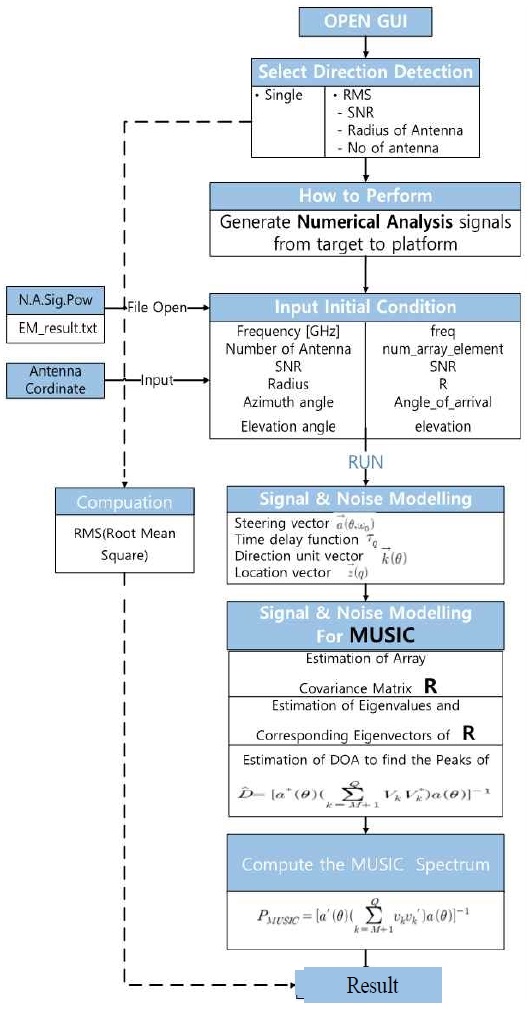
위에 설명한 신호생성 원리를 기반으로 개발된 본 통합 시뮬레이터는 그림 3에서 보이는 바와 같이 크게 메인 GUI 모듈과 전자파 해석 모듈, 그리고 방탐 추가분석 모듈의 3개의 주요 모듈과 함께외부 입·출력 장치에서 데이터를 공유할 수 있도록 공용데이터 풀(Pool)로 구성되어 있다.
메인 GUI 모듈은 시뮬레이터의 입력과 출력을 총괄하는 곳으로 프로그램에 사용되는 파라메타들의 값을 입력 팝업창을 사용하여 전달받고, 공용데이터 풀을 통해서 전자파 수치해석 결과와 3차원 모델 그래픽을 입력 받아, 메인 GUI 출력창에 3차원모델 그래픽, 안테나별 복사패턴, 안테나별 신호세기를 표시한다. 또한 상황별로 장점을 가지는 잘 알려진 고해상도 방탐기법들인 Interferometer, Correlative Interferometer, MUSIC과 Averaged MUSIC을 사용한 방탐 예측 정확도와 실측 정확도를 계산하여 메인 GUI 출력창에 표시한다.
메인 GUI 모듈은 ‘전자파해석 모듈’을 불러와서 안테나 위치와 지향각 등을 수정하여 새로운 전자파 수치해석 결과를 계산할 수 있으며, 이 때 계산된 결과는 공용 데이터 풀을 통해서 메인 GUI 모듈로 전달될 수 있다.
메인 GUI 프로그램은 안테나 개수와 SNR 등 요소별 추가적인 방탐 계산이 필요한 경우에는 ‘방탐추가 분석 모듈’을 호출하여 SNR, 시행횟수 등 각 요소별 추가항목에 대한 출력결과를 분석할 수 있도록 구성되어 있다.
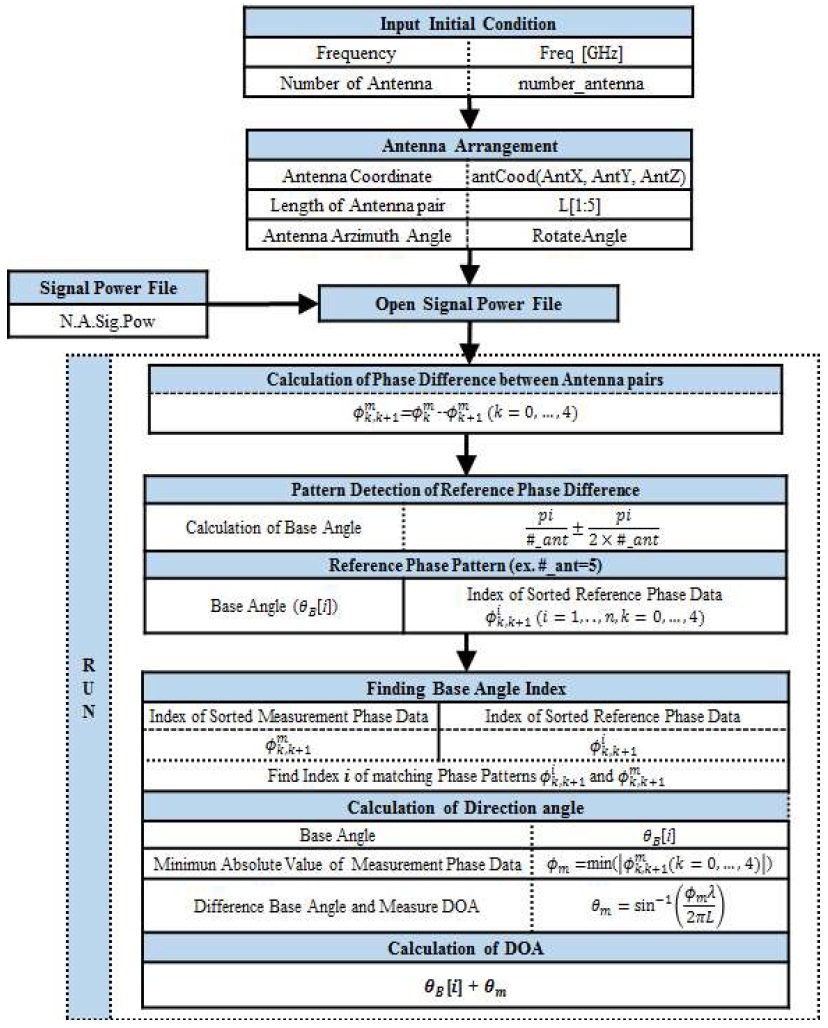
앞에서도 언급한 바와 같이 본 통합 시뮬레이터에서는 Interferometer, Correlative Interferometer, MUSIC, Averaged MUSIC의 상황별 장점들을 가지는 4가지의 고해상도 방탐 알고리즘들을 사용하였으며, 이들을 실행하기 위한 각각의 순서도를 정리하면 다음 그림 4~7과 같다.
Ⅲ. 개발된 시뮬레이터 활용 연구 결과 예
본 장에서는 개발된 통합 시뮬레이터를 활용하여 항공기에 설치된 수신 안테나 어레이로 도래하는 목표물로 부터의 신호 방향각을 최상으로 예측해 낼 수 있는 안테나 배치방안을 제시하는 과정 및 결과를 상황 예를 통하여 기술하였다. 이를 위하여 대상 항공기를 F-16 항공기로 채택하여 4:1로 축소한 모형에 대한 5개의 안테나를 원형 배열로 항공기 배열에 설치한 상태에서 안테나 어레이의 위치를 변화시키면서 MUSIC과 Averaged MUSIC 방탐 알고리즘을 이용하여 SNR 변화에 따른 RMS 방탐 오차 분석 결과를 기술하였다.
3.1 대상 항공기 모델
방탐 시스템은 F-16 항공기를 4:1로 축소한 모형에 장착한 배열안테나로부터 방탐정보를 수집하는 것으로 가정하였으며 주어진 항공기 제원은 표 2와 같다.
3.2 안테나 위치 배치
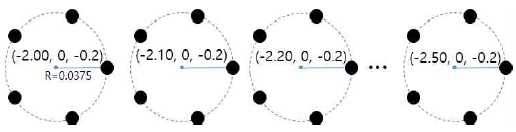
안테나 어레이는 그림 8, 9에서 와 같이 항공기의 배면에 5개의 모노폴 안테나를 원형배열로 부착하여 사용하는 것으로 가정하였으며, 최소 방탐 오차를 유발시키도록 하는 최적의 안테나 배치 선정을 위하여 그림 9와 같이 안테나 배치를 변경하되, 안테나 배열 중심의 좌표는 y축과 z축은 동일하고 x축만 0.1m씩 변경하는 것으로 하였다. 즉 (–2.00, 0 ,-0.2), (–2.10, 0, -0.2), (–2.20, 0, -0.2) (–2.30, 0, -0.2), (–2.40, 0, -0.2), (–2.50, 0, -0.2) 까지 총 6개의 좌표변화에 따른 방탐 성능분석을 수행하였다.
3.3 필요 방탐 알고리즘을 활용한 최적 안테나 배열 도출
입력 파라미터들을 표 3과 같이 설정(또는 정보전자수집체계에 의하여 파라미터 획득)하고 방탐 오차 목표치를 임의로 설정(또는 개발계획에 의거한 목표치 설정) 한 후, 선택된 방탐 알고리즘들의 적용 가능 환경을 예측하기 위하여 앞 절에서도 언급한바와 같이 그림 8 및 9와 같은 패턴으로 항공기와 안테나 배열 상태를 변화시키면서 SNR 변화에 따른 RMS 방탐 오차의 통계적 분석 결과를 개발된 통합 시뮬레이터를 이용하면 표 4에서와 같이 구할 수 있다.
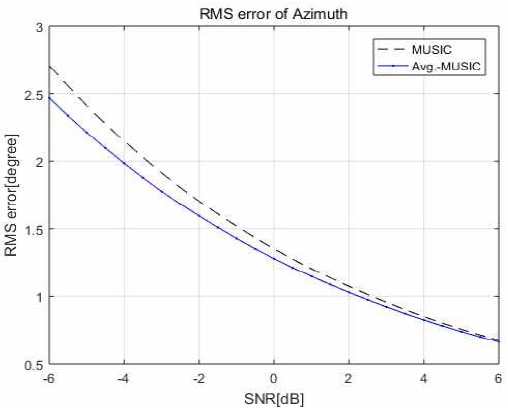
그림 10은 배열 중심 좌표 x=-2.00일 때의 SNR 변화에 따른 통계적 RMS 방탐 오차를 개발된 통합 시뮬레이터 내의 MUSIC 과 Averaged MUSIC 방탐 알고리즘을 이용하여 얻은 결과 예를 보이고 있다. 그림 10에서와 같이 동일한 과정을 이용하여 배열 안테나의 위치를 그림 9의 다른 좌표로 변경시키면서 방탐 오차 결과들을 구한 후, 임의로 설정된 방탐 오차 목표치 (본 예에서는 목표 방탐 오차 목표치를 1˚ RMS로 설정)를 만족하는 배열 안테나 좌표별 최소 SNR을 구하면 표 4에서와 같다.
여기서 알 수 있듯이, 1˚ RMS 목표 방탐오차를 얻기 위해서는 MUSIC에 비해 Averaged MUSIC을 이용할 때 더 낮은 SNR 환경에서도 우수한 방탐 성능을 보이고 있음을 알 수 있다. 아울러 안테나 배열 위치 설정 시 본 통합 시뮬레이터를 활용하여 얻어진 결과는 주어진 환경 하에서 SNR이 최소 1.9dB이상이 되는 경우에만 방탐 목표치를 달성할 수 있음을 보이고 있다.
Ⅳ. 결 론
일반적으로 안테나가 항공기 등 실제 플랫폼 위에 장착되어진 경우, 안테나간의 간섭뿐만 아니라 플랫폼으로부터 발생된 난반사를 통해 다양한 간섭현상이 발생한다. 간섭현상은 안테나 배치 형태 및 플랫폼의 기하학적 복잡성에 의해 다양한 변화가 생길 수 있다. 따라서 각각의 안테나에 수신된 신호들은 이론값과 차이가 있으며, 신호원의 방향에 따라 상의한 형태를 가진다.
이러한 실제 환경을 고려하여 개발된 본 통합 시뮬레이터는 다음과 같은 대표적인 특성을 갖는다.
첫째, 본 시뮬레이터에는 실제 항공기 플랫폼 구조물에 장착된 안테나 주변에서 감지되는 신호 및 잡음 모델을 실제 항공기 구조물의 크기, 형태, 특성, 그리고 난반사 등을 고려한 전자파 수치해석 방법을 개발하여 적용하였다.
둘째, 개발된 시뮬레이터에는 기존 고해상도 DOA 예측기법들 중 서로 장단점을 가지는 4가지의 고해상도 방탐 기법들(Interferometer, 상관형 Interferometer, MUSIC, Averaged MUSIC)을 선정한 후, 이들을 최적으로 활용하기 위하여 항공기 방탐에 필요한 파라미터 입력 시 최적의 안테나 배치 및 안테나 개수에 대한 정보를 도출하도록 하였다. 또한, 본 시뮬레이터의 성능을 다각적으로 분석할 수 있도록 이론적 시행 및 전자파 수치해석적 시행을 위한 기능을 장착하였고, 각 시행마다 단일 분석 기능과 통계적 분석 기능을 두어 개략적 방탐 분석 및 상세 방탐 분석을 할 수 있도록 하였다.
표 5는 본 통합 시뮬레이터에서 사용된 4가지 방탐 방식의 방탐 정확도와 측정 소요시간 등의 관점에서 다각적으로 비교 분석한 결과를 정리한 것으로서, 필요에 따라 방탐 기법들을 선택하여 사용할 수 있다.
본 통합 시뮬레이터는 운용자가 실제 시스템 개발 및 활용 여부를 결정하기 위한 필요 데이터를 상황이나 환경별로 미리 예측하는 참고자료로 요긴하게 사용될 수 있을 것으로 기대된다.
Acknowledgments
본 연구는 광주과학기술원 전자전특화연구센터를 통한 방위사업청과 국방과학연구소 연구비를 지원받아 연구됨.
References
- S. U. Pillai, and C. S. Burrus, "Array Signal Processing", Springer-Verlag, p221, (1989).
- I. K. Rhee, "Aircraft-Based Optimal Direction Detection Algorithm", Hannam University, Network Customizing Technology Inc, p3-19, Jun.), (2011.
- S. C. Jeong, L. W. Baek, and I. K. Rhee, "Performance Analysis of Averaged-MUSIC Algorithm applied to Circular Antenna Array", The Institute of Electronics and Information Engineers, p51-52, Dec.), (2016.
-
R. O. Schmidt, "Multiple Emitter Location and Signal Parameter Estimation", IEEE Trans. on Antennas and Propagation, AP-34(3), p276-280, Mar.), (1986.
[https://doi.org/10.1109/tap.1986.1143830]

- I. K. Rhee, I. K. Choi, Y. J. Kim, and C. S. Kang, "A Study on Performance Analysis of High Resolution DOA Method based on MUSIC", The Journal of the KICS, 19(2), p345-353, Feb.), (1994.
- S. M. Kamal, A. A. Adam, and A. S. Ajagun, "Performance Evaluation of Correlative Interferometry for Angle of Arrival Estimation", Journal of Emerging Trends in Engineering and Applied Sciences, 6(1), p43-48, Feb.), (2015.
-
Ting Cheng, Xintao Gui, and Xin Zhan, "A dimension separation-based two-dimensional correlation interferometer algorithm", EURASIP Journal on Wireless Communications and Networking, 2013(1), p1-10, Dec.), (2013.
[https://doi.org/10.1186/1687-1499-2013-40]

- A. K. Bhattacharyya, "High-Frequency Electromagnetic Techniques: Recent Advances and Applications", Wiley-Interscience, Aug.), (1995.
-
G. A. Thiele, and T. M. Newhouse, "A Hybrid Technique for Combining Moment Methods with the Geometrical Theory of Diffraction", IEEE Transactions on Antennas and Propagation, 23(1), p62-69, Jan.), (1975.
[https://doi.org/10.1109/tap.1975.1141004]

-
E. P. Ekelman, and G. A. Thiele, "A Hybrid Technique for Combining the Moment Method Treatment of Wire Antennas with the GTD for Curved Surfaces", IEEE Transactions on Antennas and Propagation, 28(6), p831-839, Nov.), (1980.
[https://doi.org/10.1109/tap.1980.1142423]

-
W. C. Gibson, "The Method of Moments in Electromagnetics", Chapman and Hall/CRC, p450, Jul.), (2014.
[https://doi.org/10.1201/b17119]

-
R. F. Harrington, "Field computation by moment methods", Holtzbrinck Publishing Group, p240, (1968).
[https://doi.org/10.1109/9780470544631]

- D. A. McNamara, C. W. I. Pistorius, and J. A. G. Malherbe, "Introduction to the Uniform Geometrical Theory of Diffraction", Artech House, p471, (1990).

2014년 2월 : 한남대학교 전자공학과(학사)
2018년 3월 ~ 현재 : 한남대학교 전기전자공학과(석사)
관심분야 : 어레이 신호처리(방향탐지 장치)

2007년 3월 : 한국해양대학교 전파공학과(학사)
2013년 9월 : 광주과학기술원 기전공학부(석사)
2015년 9월 ~ 현재 : 광주과학기술원 기계공학부(박사)
관심분야 : 전자파 수치해석

1982년 2월 : 경북대학교 전자공학과(학사)
1986년 6월 : 미국 Oregon State University 전자공학과(석사)
1990년 2월 : 미국 Oregon State University 전자공학과(박사)
1990년 3월 ~ 현재 : 한남대학교 전기전자공학과 교수
관심분야 : 어레이 신호처리, 스펙트럼 분석 및 관리

1978년 2월 : 경북대학교 전자공학과(학사)
1987년 7월 : 충남대학교 전자공학과(석사)
1994년 3월 : Auburn University 전기공학과(박사)
1980년 8월 ~ 2003년 12월 : 국방과학연구소
2003년 3월 ~ 현재 : 백석대학교 정보통신학부 교수
관심분야 : 전자파 이론, 방향탐지장치 설계

1993년 2월 : 홍익대학교 전자전산기공학과(학사)
1995년 8월 : 홍익대학교 전자공학과(석사)
2016년 2월 : 홍익대학교 전자공학과(박사)
2007년 3월 ~ 현재 : 백석대학교 정보통신학부 강사
관심분야 : 방향탐지 알고리즘, 데이터 사이언스

2012년 2월 : 충남대학교 전파공학과(학사)
2014년 2월 : 충남대학교 전파공학과(석사)
2014년 2월 ~ 현재 : 국방과학연구소 선임연구원
관심분야 : 주파수 합성기, 광대역 수신기 등