Real-time Moving Object Detection Based on RPCA via GD for FMCW Radar

Ⅰ. Introduction

Moving-target detection is a common and critical task for security systems. When estimating moving-targets’ information such as distance and velocity, Frequency Modulated Continuous Wave (FMCW) radar is considered to be the choice [1]. Range information can be extracted via demodulation of the frequency signal, and velocities of moving-targets are computed via Doppler Effect. However, moving-target detection is a serious challenge, especially in complex environments. The detection results are sensitive to noise and clutter resulting from small moving objects in radar scan areas or from multipath problems. In addition, strong reflection signals from large static objects are also considered as a type of noise. These issues may significantly degrade the radar’s capability in practical applications.

There are several ways to detect moving objects by FMCW radar. In [2], the authors proposed using a de-interleaved method in the time domain and a different number of Fast Fourier Transform samples to improve the range and velocity of the detection results. Another method based on 2-D FFT with fast-ramp training was proposed in [3]. A technique based on a constant false alarm rate (CFAR) algorithm [4] was introduced to reduce the effect of noise. Waveform design was a good solution to improve the results of the noise reduction and multiple targets detection [5]. Another method based on a machine learning technique to model the background and extract the moving foreground using Gaussian Mixture Model with FMCW radar was presented in [6].

Various approaches have been explored to solve the moving-object detection problem. Among them, Robust Principal Component Analysis (RPCA) based on low-rank matrix decomposition algorithms have been showed impressive results [7]. However, RPCA batch optimization processing are computationally complex and require a large memory. In [8], Inexact Augmented Lagrange Multipliers (IALM) approach was defined and converged to solve the RPCA problem. Moreover, Feng and Xu [9], recently proposed Online-Robust PCA (OR-PCA) algorithm which was able to process one sample per time immediately based on stochastic approximation in order to reduce the processing time. A new method to solve RPCA problem by using Gradient Descent (RPCA-GD) was presented in [10]. They achieved remarkable performance in both accuracy and computational cost.

Inspired by these achievements, this paper examines the ability of RPCA-GD in modelling the noisy background for a FMCW radar data based on the sliding window method. More notably, a new online updating method is proposed for real-time applications. The proposed algorithm shows outstanding results in comparison with the baseline RPCA-GD and other RPCA-based approaches. The main contributions in this work are summarized as follows.

• 1. The background modeling ability of RPCA via GD approach is investigated in detail.
• 2. A new updating method is proposed for real-time moving-object detection using FMCW radar system.
• 3. Various experimental scenarios are conducted to show the effectiveness of proposed algorithm in both accuracy and processing speed terms.

The remainder of this paper is organized as follows. The data collection method is addressed in Section II. Section III presents the reason why we propose a new computational method. The details of our work are provided in section IV. The experimental evaluation and conclusion are presented in section V and section VI, respectively. The list of key notations used in this paper is provided in Table 1.

Table 1.

Key notations

Ⅱ. Data Collection Method

Data collection method is introduced in this section. We focus on moving objects detection in short range about 10 meters. Therefore, the FMCW radar based on a 120GHz is selected. The radar front-end is connected to the SiRad Easy Evaluation Kit [11].

The system setup to gather reflected signals from moving objects in experimental environments is depicted in Fig. 1. The input data is recorded and sent directly to PC via UART cable for saving and evaluation. In practical applications, all processing steps are implemented as an online processing method.

Fig. 1.

System setup for collection data

By using SiRad Easy Evaluation Kit, we are able to set several parameters including bandwidth, number of Fast Fourier Transform (FFT) points, and number of ramps. The output of this system is a block of data which contains system information, status information, FFT values and constant false alarm rate (CFAR) data, target and error information. The graphical user interface (GUI) is provided by Silicon Radar Company for setting technical parameters. These setting parameters can be controlled via UART interface [11]. Selected technical parameters are given in Table 2.

Table 2.

Setup parameters

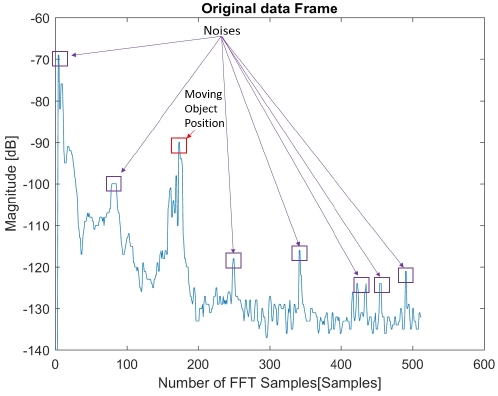
For each cycle, the block data will be extracted to different data frames based on start and stop bits. In this paper, original FFT values are extracted for further processing. FFT data frame is stored as a column vector with N elements. The illustration of data in one data frame is depicted in Fig. 2. We can observe that there are various noise points leading to miss detection and false alarm problems when we detect the moving objects.

Fig. 2.

Ilustration of one FFT data frame

The main task is extract the position of the moving objects based on the input data frames. After T cycles, the received data is saved as a matrix X∈$$ \mathbb{R}$$^N×T. We apply our approach on matrix X to get moving object positions and update these values after each frame. The processing detail is provided in Section IV.

Ⅲ. Rationale of the Proposed Approach

There are various approaches to separate the static background and moving foreground objects. As aforementioned, RPCA is selected to model the background due to its admirable performance. The main purpose of RPCA approach is to decompose the observation matrix X∈$$ \mathbb{R}$$^N×T into a low-rank matrix L with rank r, which is represented the static background, and a sparse component matrix S, which is modeled targets, by Eq. (1). The original FFT data is recorded and save as a matrix X after T cycles X∈$$ \mathbb{R}$$^N×T. We recognize that the reflecting signals from static objects are almost similar at all time which is called “background” or low-rank matrix L. Conversely, moving objects are able to consider as a sparse matrix S or “foreground”. In next frames, the input matrix is updated by sliding window approach. Our goal is to recover L and S from X by solving the convex relaxation in Eq. (2) [12].

where ∥L∥_* is the nuclear norm of matrix L, $$ {‖S‖}_1=\sum _{i,j}\left|S_{ij}\right|$$, and λ is the positive weighting parameter.

Numerous algorithms have been developed to solve Eq. (2). However, the RPCA algorithms are difficult to apply for real-time application because of the need to handle all data whenever new data frame has been inserted. The computational cost increases when the size of the data growths, respectively. Applying the sliding window approach to investigate the ability of RPCA on a radar signal was presented in [13]. According to that study, as the new frame was captured, RPCA was adopted on the window matrix to model the background. We realize that their approach is not effective for a time sequence signal as the radar signal due to re-compute low rank components for entire window matrices. The method proposed in this paper is based on the following observation: as the new frame is inserted, the low-rank component matrix changes a little compared to the previous calculation. The computed low-rank matrix from previous step is used and adapted the last column vector as initialization matrix for optimization.

Ⅳ. Methodology development

4.1 Overview of the Proposed Method

This section presents the details of our scheme to detect moving foreground objects. Time-based sliding window approach is implemented to process the raw input data, as shown in Fig. 3. We fix size of the window to M and process the window matrix Y∈$$ \mathbb{R}$$^N×M. In this approach, the initial window matrix M is first accumulated via raw data vectors. All processing step is applied on the initial window matrix.

Fig. 3.

Time-based sliding window approach

In the next cycle, the new data frame are added to matrix M, and the oldest data frame is discarded. We re-compute on new window matrix M.

Each window matrix is processed via three main steps, as illustrated in Fig. 4. The input data frame is calibrated and compensated based on experiments in pre-processing step. The received signal power from target decreases when the target mover farther away from radar called Path Loss Compensation. Based on practical experiments, we select the compensation factor as log₁₀(4πR²). The received signal at each point is weighted of log₁₀(4πR²). RPCA-GD is used to model the background. A novel method to updates the initial background for RPCA when each new frame has been accumulated is proposed. Finally, moving foreground objects’ positions are estimated using AMPD peak detection algorithm [14].

Fig. 4.

Illustration of proposed method

4.2 Background modeling based on RPCA-GD

In this section, we describe our novel algorithm for modeling the background based on RPCA in real-time. The basic idea is updating method to generate initial matrix based on the previous processing. The Online RPCA via GD is presented in Algorithm 1. First, we collect data for processing until t = M. When t = M, we utilize the method in [10] to extract the low-rank component.

Algorithm 1:

Online RPCA via GD

S_init is generated based on the input window matrix Y using a sorting-based sparse estimator algorithm which basically conducted as follows for any matrix A∈$$ \mathbb{R}$$^d1×d2.

$\[ {\mathfrak{J}}_{\alpha }\left[A\right]≔\left\{\begin{array}{c}{A}_{\left(i,j\right)}, \text{if}\left|A_{\left(i,j\right)}\right|\ge \left|A_{\left(i,.\right)}^{\left(\alpha d2\right)}\right|\text{and}\left|A_{\left(i,j\right)}\right|\ge \left|A_{\left(.,j\right)}^{\left(\alpha d1\right)}\right|,\hfill \\ \begin{array}{cc}0,\hfill & otherwise\hfill \end{array}\hfill \end{array}\right. \]$

(3)

where $$ A_{\left(i,.\right)}^{\left(k\right)}$$ and $$ A_{\left(.,j\right)}^{\left(k\right)}$$ denote the elements of A_(i,.) and A_(.,j) that have k-th magnitude, respectively.

After generating S_init Single Value Decomposition (SVD) method is applied on (Y - S_init) to obtain the matrix rank r.

$\[ \left[H,\mathrm{\Sigma },K\right]=SVD\left(Y-S_{init}\right) \]$

(4)

Let’s U_t←HΣ^1/2, V_t←KΣ^1/2, we consider the following optimization problem.

$\[ \underset{U,V,S}{\min }\zeta \left(U,V;S\right)+\frac{1}{8}{‖U{U}^T-V^{T}V‖}_F^2 \]$

(5)

With a given U_t,V_t, an iterative method is implemented to produce the sparse matrix S based on sparse estimator on $$ S_t={\mathfrak{J}}_{\gamma \alpha }\left(Y-U_t{V}_t^T\right)$$. The projected gradient descent is computed as following equations to produce U_nw, V_nw.

$\[ U_{nw}=\begin{array}{c}{\Pi }_u\left(U_t-\eta {\nabla }_{U}L\left(U_t, V_t;S_t\right)\right.\\ -\frac{1}{2}\eta U_t\left.\left(U_t^T{U}_t-V_t^T{V}_t\right)\right)\end{array} \]$

(6)

$\[ V_{nw}=\begin{array}{c}{\Pi }_u\left(V_t-\eta {\nabla }_{V}L\left(U_t, V_t;S_t\right)\right.\\ -\frac{1}{2}\eta V_t\left.\left(V_t^T{V}_t-U_t^T{U}_t\right)\right)\end{array} \]$

(7)

where γ and η the algorithmic tuning parameters. The loss function $$ \mathcal{L}$$(U,V,S) is defined as follows

$\[ \mathcal{L}\left(U,V;S\right)≔\frac{1}{8}{‖U{V}^T+S-Y‖}_F^2 \]$

(8)

Finally, the low-rank and sparse matrices is updated in Phase 3. More details can be found in [10].

Continuously, Algorithm 2 is proposed to update and initialize U_t, V_t from frame t = M+1. The oldest column is removed based on a sliding window approach. The basis update algorithm includes three steps. First, last vectors are extracted from previous calculation U_t-1, V_t-1. These vectors are added to initial matrix U_t, V_t. Finally, we discard the oldest vectors U_t, V_t. The updated matrices U_t, V_t are utilized as initial matrices for optimization based on the Gradient Descent method. This critical initial step saves the computation cost to optimize U_t, V_t. Other steps are re-implemented as in phase 2 and phase 3 of Algorithm 1.

Algorithm 2:

The basis update of initial matrix

Ⅴ. Evaluation

We conduct our experiments in various environments with multiple targets moved with different tracks and speeds as shown in Fig. 5. In each scenario, the data is captured and saved to evaluate and compare the performances on RPCA-based approaches. The experiments are executed in Matlab using the PROPACK toolbox and tested on an Intel Core i7-2620M at 2.70GHz with 8GB of RAM. The precision (Pr), recall (Re), and F1-measure (F1) metrics were selected to evaluate system performance.

Fig. 5.

Experimental scenarios

These values are computed from True Positive (TP), False Positive (FP), and False Negative (FN). The calculations are given in Table 3.

Table 3.

Calculations of system performance

5.1 Performance across different approaches

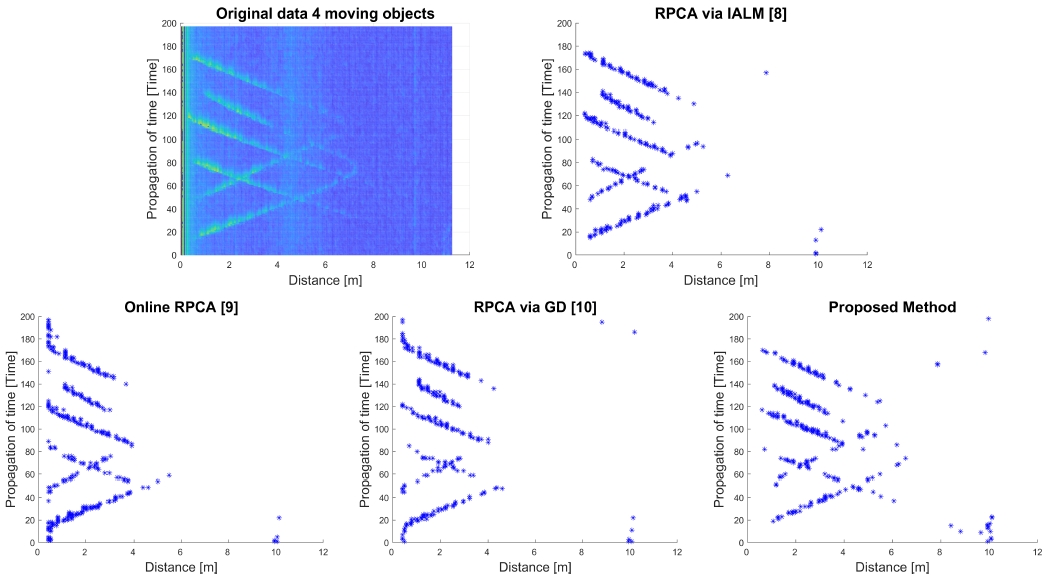
To examine the performance of proposed method on FMCW radar signal, we execute sliding window approach on RPCA via IALM [8], online RPCA [9] and RPCA via GD [10] and the proposed method with a window size M = 50, number of iteration of 100, rank r = 10, and stop criteria of 0.02 for evaluation. An illustration of four moving-target detections is depicted in Fig. 6. The original data includes noise which is reflected from other objects in the first row. There are 4 moving targets in this experimental scenario. Two targets move from radar to further away and come back, which make the V shape. Two other objects just go further for detection range, which make I shape. The experimental environment includes noises, as marked in Fig. 6, which make the detection task more challenge. The detection results are shown in the second row for comparison. From the original data in the first row, the power of noise is very high in range of 4 to 6 meters. When the object move further away over 6 meters, due to the noise, other RPCA-based methods are not able to detect the object.

Fig. 6.

Illustration of detection performance.

However, our proposed method is still able to extract the moving objects. The blue points in Fig. 6 are the extracted position of moving objects. The detection performances are presented in Table 4 and Table 5. The proposed method reaches up to 89.5% in precision, 80.0% and 84.4% in recall and F1-measure, respectively. RPCA via IALM approach obtains the highest accuracy. However, this method is too slow for real-time application with processing speed of only 0.6 frames per second. Compared to the Online RPCA, the proposed method significant outperform in performance term at 6.7%, 5.0% and 5.9% of precision, recall and F1-score.

Table 4.

Detection performance across different methods.

Table 5.

Processing speed across different methods.

Furthermore, the baseline RPCA via GD obtains lower results in compare with the proposed method in both processing speed and accuracy. Our proposed method improve the baseline RPCA via GD [10] method up to 4.2%, 3.2% and 3.7% of precision, recall and F1-score, respectively. The original RPCA via GD is unable to apply in real-time applications due to processing speed is only 1.1 frame per second. Conversely, with the proposed updating algorithm, our system can work in real-time applications with processing speed up to 19 frames per second. There are three main reasons.

First, the initial matrix in our approach is based on a previous observation, which leads to reducing the processing time to obtain optimal results. Second, in other approaches, the initial matrix based on an SVD approach is re-computed when each new data was added which bring out higher consumption cost. Third, the low rank matrix in the current frame is not significantly different from the previous one when the new vector is added. Therefore, we do not have to re-compute the low rank matrix from beginning.

5.2 Impact of sliding window size

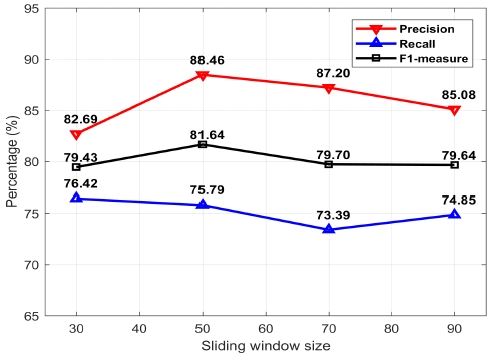
The impact of different the window size is evaluated in this section. We select the rank r = 10. The window size is varied from 30 to 90. The system performances are shown in Fig. 7. The system achieves 88.46% of precision, 75.79% and 81.64% of recall and F1-measure, respectively, with M = 50. When the siding window size is 30, there is too little data to model the low-rank background.

Fig. 7.

Impact of the sliding window size

Therefore, the system performance get worse at M = 30 with 82.69% of precision, 76.42% of recall, and 79.43% of F1-measure. When the processing matrix size increases, the system performance also enhances due to the dissimilarity between the low-rank and the sparse matrix. When the matrix size was too large, the optimization step reached the maximum iteration value before obtaining optimization matrix. For that reason, the performance decreases when the matrix size increases, such as M = 70 or M = 90. On the other hand, the computational cost is high with a large input matrix. Due to real-time processing requirements, the window size is selected as 50 for other evaluations.

5.3 Impact of the number of iteration

Another critical parameter which has an effect on the system performance is the number of iteration. In this experiment, we investigate the detection accuracy by changing the number of iteration from 10 to 150. The processing matrix size M is equal to 50, and the rank of the processing matrix was 10. The selected number of iteration includes 10, 30, 50, 70, 90, 110, 130, and 150 iterations. The system performance is sketched in Fig 8.

Fig. 8.

Impact of the number of iteration

The system obtains up to 89.07% in precision, 75.04% of recall and 81.46% of recall with 110 iterations. The detection accuracy is significantly enhanced when the number of iteration changed from 10 to 30. The main reason is that with 30 iterations, the initialized matrix does not achieve optimized values. There is still existing space to improve the system performance based on an increase in the number of iterations. From 30 to 150, the system performance almost do not change because the system reaches the optimal solution at the first initialization.

5.4 Performance across different updating methods

We also analyze the impact of different updating methods in Algorithm 2 to investigate the efficiency of the Basis update algorithm. This evaluation is conducted based on three different update methods: average method, weighted method and update from the latest low-rank vector.

In the average method, we compute the average value vector from a previous observation of the U_t, V_t matrix. We add these vectors to the last column and discard the oldest vector, as in Algorithm 2. The average method is a specific case of a weighted method with all values having the same weight. In the weighted mean method, we insert the weight to each column vector based on its position as follows.

$\[ w_i=\frac{i}{\sum _{i=1}^{r}i\text{'}} \]$

(9)

where w_i is the weight for the i-th column, and r is the rank of the matrix as in the initialization.

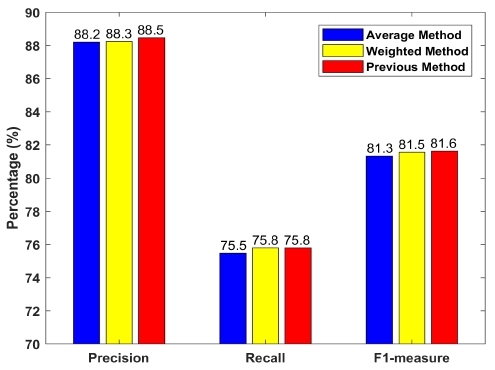
In the last case, we simply add the previous vector and remove the oldest vector when the new frame is inserted, as mentioned in Algorithm 2. Experimental results are shown in Fig. 9. According to Fig. 9, the updating method using a previous frame obtained the best performance with up to 88.5% of precision, 75.8 % and 81.6% of recall and F1-measure, respectively. The worst case use an average updating method with 88.2% of precision, 75.5% of recall and 81.3% of F1-measure. The similarity in the low-rank matrix between the previous and current update increases in the following order: average method, weighted method and previous method. Based on this property, the system performance increase in this order from the average method to the previous method. The difference between these updating methods is very small, and it mainly depends on the initial low-rank matrix in the first step.

Fig. 9.

Detection performance across different update methods

5.5 Performance in multiple moving objects with velocity variation

The robust of proposed algorithm is proofed by several scenarios containing multiple moving objects with different velocities. Two objects move with different speeds (slow walking and normal walking) and distance are called scenario 1 and scenario 2, accordingly. Furthermore, three and four moving objects with different speeds (slow walking, walking and running) and various tracks are presented in scenario 3 and scenario 4, respectively. The numerical results of each scenario and average performance are shown in Table 6. We compare the performance of proposed method with other RPCA-based method such as RPCA via IALM [8] and RPCA via GD [10] and Online RPCA [9]. Our proposed method achieves comparable results with RPCA via IALM [8] with sliding window approach. In comparison to the baseline RPCA via GD [10], our method obtains better performance in all precision, recall and F1-measure metrics. Online RPCA [9] can not remove noises perfectly. As a result, Online RPCA [9] shows worst performance. As mentioned in Section 5.1. Our proposed method is able to works at real-time speed. From these experiments, our proposed approach is the best solution for practical applications due to high accuracy and good processing speed.

Table 6.

Detection results on various speeds across different methods.

Ⅵ. Conclusion

This paper proposed an approach for detecting moving-target using FMCW radar in a noisy environments based on RPCA approach. We introduced a novel updating method to reduce the computational cost for the time sequence dataset such as collected data from radar sensor. Through various evaluation experiments, the proposed approach showed the effectiveness in different scenes and outperforms other RPCA based techniques.

Acknowledgments

This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2019-2016-0-00314) supervised by the IITP

References

• C. Li, Z. Peng, T. Y. Huang, T. Fan, F. K. Wang, T. S. Horng, J. M. Muñoz-Ferreras, R. Gómez-García, L. Ran, and J. Lin, "A review on recent progress of portable short-range noncontact microwave radar systems", IEEE Trans. Microw. Theory Techn, 65(5), p1692-1706, May), (2017. [https://doi.org/10.1109/tmtt.2017.2650911]
• E. Hyun, and J. H. Lee, "Method to improve range and velocity error using de-interleaving and frequency interpolation for automotive FMCW radars", IJSIP, p11-22, Feb.), (2009.
• M. Song, J. Lim, and D. J. Shin, "The velocity and range detection using the 2D-FFT scheme for automotive radars", In Proceedings of 4th IEEE International Conference on Network Infrastructure and Digital Content (IC-NIDC), Beijing, China, 19–21, p507-510, Sep.), (2014. [https://doi.org/10.1109/icnidc.2014.7000356]
• M. Kronauge, and H. Rohling, "Fast two-dimensional CFAR procedure", IEEE Trans. Aerosp. Electron. Syst. 2013, 49, p1817-1823, (2013). [https://doi.org/10.1109/taes.2013.6558022]
• J. Li, W. Che, T. Shen, W. Feng, X. Li, and K. Deng, "An improved waveform for multi-target detection in FMCW vehicle radar", In Proceedings of the 7th International Conference on Mechatronics, Control and Materials (ICMCM), Changsha, China, 29-30, p203-206, Oct.), (2016. [https://doi.org/10.2991/icmcm-16.2016.41]
• Y. Zhao, and Y. Su, "Vehicles detection in complex urban scenes using Gaussian mixture model with FMCW radar", IEEE Sensors J., 17, p5948-5953, (2017). [https://doi.org/10.1109/jsen.2017.2733223]
• T. Bouwmans, A. Sobral, S. Javed, S.K. Jung, and E. H. Zahzah, "Decomposition into low-rank plus additive matrices for background/foreground separation: A Review for a Comparative Evaluation with a Large-Scale Dataset", Computer Science Review, 23, p1-71, (2017). [https://doi.org/10.1016/j.cosrev.2016.11.001]
• Z. Lin, M. Chen, and Y. Ma, "The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices", (2009).
• J. Feng, H. Xu, and S. Yan, "Online robust PCA via stochastic optimization", Proc. NIPS 2013, p404-412, Dec.), (2013.
• X. Yi, D. Park, Y. Chen, and C. Caramanis, "Fast algorithms for robust PCA via gradient descent", (2016).
• Silicon radar, http://siliconradar.com/ [accessed: Feb. 00, 2019].
• E. J. Candès, X. Li, Y. Ma, and J. Wright, "Robust principal component analysis?", J. ACM, 58(1), p1-37, (2011).
• D. Sabushimike, S. Y. Na, J. Y. Kim, N. N. Bui, K. S. Seo, and G. G. Kim, "Low-rank matrix recovery approach for clutter rejection in real-time IR-UWB radar-based moving target detection", Sensors, 16, p1409, (2016). [https://doi.org/10.3390/s16091409]
• F. Scholkmann, J. Boss, and M. Wolf, "An efficient algorithm for automatic peak detection in noisy periodic and quasi-periodic signals", Algorithms, 5, p588-603, (2012). [https://doi.org/10.3390/a5040588]