심층 합성곱 신경망에 기반한 이미지 바코드의 은닉 데이터 디코딩 기법

2.1 이미지 모멘트 기반의 디코딩 기법

이미지 모멘트 기반의 디코딩 기법은 이미지 바코드에 은닉된 데이터를 복원하기 위해 이미지 모멘트라 불리는 척도를 사용한다. 이미지 모멘트는 아래와 같이 계산된다[4].

식 (1)에서 I^H(x,y)는 이미지 바코드를 의미하고 C는 셀(Cell)이라 불리는 6×6 또는 8×8 크기의 픽셀 영역에 해당한다. 그리고 (x,y)는 2차원 픽셀 좌표이다. 식 (2)는 (x,y) 좌표 값을 각도 θ_i만큼 회전한 좌표계의 값을 나타낸다. 여기서 θ_i는 0°또는 90°둘 중 하나의 값을 가진다. 식 (3)인 $$ {\overline{u}}_i$$는 해당 셀에서 밝기의 무게 중심 값에 해당한다. 따라서 식 (1)에서 $$ {\left(u_i-{\overline{u}}_i\right)}^2$$는 밝기 차가 얼마나 큰지를 나타내는 성분이므로 하프톤 셀의 도트 패턴의 방향이 가로 방향인지 세로 방향인지를 판별할 수 있다. 좀 더 구체적으로 말하면, σ₁>σ₂일 경우에는 셀 내의 도트 패턴이 가로 방향의 도트 패턴으로 인식하고, σ₂>σ₁일 경우에는 셀 내의 도트 패턴이 세로 방향의 도트 패턴으로 간주한다.

식 (2)에서 보듯이, 이미지 모멘트는 한 쪽 방향으로 밝기의 편차가 심한 도트 패턴, 예를 들어 가로 및 세로 방향의 도트 패턴을 구별하기에 적합하다. 따라서 이미지 모멘트 척도는 다양한 도트 패턴에는 적용하기가 어렵다.

2.2 희소 표현 기반의 디코딩 기법

동일한 부류에 속한 도트 패턴들은 특정 기저 벡터들(Basis Vectors)의 조합으로 표현이 가능하다. 이는 다른 부류에 속한 도트 패턴들은 이 기저 벡터들로는 표현할 수 없음을 의미한다. 따라서 각 부류에 소속된 도트 패턴들을 표현할 수 있는 기저 벡터들을 학습한 후, 입력 도트 패턴을 재복원해서 그 복원율의 정확도로 입력 도트 패턴을 분류하는 것이 가능하다. 이런 방식으로 도트 패턴을 분류하는 기법을 희소 표현 기반의 분류 또는 희소 표현 기반의 디코딩 기법[5] 이라 불린다. 이 기법은 크게 훈련영상으로부터 도트 패턴의 기저벡터를 생성하는 사전 학습(Dictionary Learning) 과정과 주어진 기저벡터를 사용해서 입력 도트 패턴을 재구성(Reconstruction)하는 희소 코딩 과정으로 이루어진다. 먼저, 사전 학습 과정은 아래와 같이 표현된다.

여기서 Y는 훈련 패치를 포함한 행렬이고 D와 A는 추정해야 될 사전과 희소 코드 행렬이다. 그리고 j는 도트 패턴의 종류를 구분하는 인덱스이다. 즉, j가 H일 경우에는 가로 방향의 도트 패턴을 가리키고 j가 V일 경우에는 세로 방향의 도트 패턴을 가리킨다. 따라서 식 (4)에서 D^j는 가로 및 세로 방향의 도트 패턴 별로 학습이 된다. Y^j는 수집된 훈련 영상에서 하프토닝을 적용하여 추출한 패치를 열벡터로 저장하고 있다. 식 (4)에서 첫 번째 항목은 Y가 DA로 표현할 수 있다는 데이터 충실도(Data Fidelity) 제약 조건으로써, Y의 열벡터가 D에 저장된 열벡터, 즉 기저 벡터들의 선형조합으로 표현될 수 있음을 나타낸다. 두 번째 항목은 희소 제약 조건이다. 벡터 α_i는 A행렬의 i번째 열벡터로써, 대부분의 벡터 요소의 값이 영인 제약 조건을 가진다. 벡터에서 영이 아닌 벡터 요소의 개수는 ℓ₀-놈(Norm), 즉 ‖α_i‖₀로 표현이 가능하다. 따라서 희소 제약 조건은 ‖α_i‖₀가 특정 문턱치인 TH 보다 작게 설정하면 된다. 이 논문에서는 식 (4)를 풀기 위해 K-SVD 사전 학습 기법을 사용하였다[7]. 사전 학습을 통해 두 종류의 도트 패턴에 대한 사전 D^H와 D^V가 주어진 경우, 입력 도트 패턴을 구분하기 위해 희소 코딩 과정이 수행된다.

여기서 y는 입력 도트 패턴으로 갖는 패치이고 D^j는 학습된 사전에 해당한다. 따라서 식 (5)는 입력 패치 y가 D^jα로 표현되고 α가 희소 제약 조건을 만족해야 됨을 말한다. 식 (5)는 경사 추적(Gradient Pursuit) 기법 [8]을 사용해서 풀 수 있다. 입력 도트 패턴이 가로 방향의 도트 패턴인지 세로 방향의 도트인지는 복원율의 정확도를 비교해서 판별할 수 있다. 예를 들어 입력 패치 y가 가로 방향의 도트 패턴일 경우에는 D^H로 복원된 패치, D^Hα의 복원의 정확도가 높을 것이다. 그러나 D^V로 복원하면 상대적으로 복원의 정확도가 낮을 것이다. 이런 희소 표현 기반의 디코딩 기법은 비단 가로 및 세로 방향의 도트 패턴에만 국한되지 않고 다양한 도트 패턴에도 적용될 수 있다. 하지만 도트 패턴의 분류에 대한 정확도 측면에서는 여전히 개선할 여지가 있다.

3.1 디더링 기반의 하프토닝

앞서 언급했듯이 하프토닝은 연속 계조 영상을 흰색과 검정색의 도트 패턴으로 구성된 이진 영상을 생성하는 과정이다. 그림 2는 하프토닝 기법을 적용한 예시를 보여주고 있다. 왼쪽 그림은 입력 영상이고 오른쪽 그림은 하프톤 영상이다. 우측 하단의 빨간색 박스에서 보듯이, 흰색과 검정색 도트가 군집을 이루어 형성된 것을 볼 수 있다. 이런 도트 패턴은 군집 하프톤 도트 패턴이라 불린다.

Fig. 2.

(a) Input image, (b) Halftoned image

하프톤 기법에는 디더링(Dithering), 오착 확산(Error Diffusion), 직접 이진 검색(Direct Binary) 등이 있다[9]. 본 논문에서는 디더링 기반의 하프토닝 기법을 사용하고 한다. 디더링 기법은 디더링 행렬의 값과 원본 영상의 픽셀 값을 일대일로 비교해서 하프톤 영상을 생성한다. 만약, 입력 영상의 픽셀 값이 디더링 행렬의 값보다 크면 ‘255’의 값으로 변환하고, 그렇지 않으면 ‘0’의 값으로 변환한다. 이 과정을 통해 입력 영상이 도트 패턴으로 구성된 이진 영상으로 변환하게 된다. 보다 자세한 사항은 참고 문헌[10]을 보시기 바란다.

3.2 이미지 바코드 생성

그림 3은 이미지 바코드 생성을 위해 필요한 입력 영상과 은닉 데이터의 예시를 보여주고 있다.

Fig. 3.

(a) Original image for image barcode generation, (b) Hidden image into image barcode

은닉 데이터는 그림 3(b)와 같이 흑백 영상이다. 흑백 영상은 ‘0’ 또는 ‘255’ 픽셀 값으로 구성되어 있다. 이는 흑백 영상이 ‘0’과 ‘1’로 구성된 비트시퀀스로 표현될 수 있음을 의미한다.

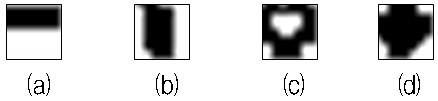
이미지 바코드는 은닉 데이터의 값, 즉 ‘0’ 또는 ‘255’ 값에 따라 디더링 행렬을 선택한 후, 하프토닝 과정을 적용하면 생성된다. 그림 4는 네 종류의 디더링 행렬을 보여준다. 이미지 바코드 생성 단계는 이미지 바코드 생성에 필요한 입력 영상, 은닉 데이터, 디더링 행렬이 주어지면, 다음과 같이 수행된다.

Fig. 4.

Dithering matrixes for generating four types of dot patterns; (a) Horizontal dot patterns, (b) Vertical dot patterns, (c) Circular dot patterns, (d) Dual dot patterns

◆ 1단계: 은닉 영상에서 픽셀 값 하나를 읽어 와서 그림 4에 보이는 디더링 행렬 중에 하나를 선택한다. 예를 들어, 은닉 영상에서 픽셀 값이 ‘0’이면 그림 4(a)의 세로 방향 도트 패턴 생성을 위한 디더링 행렬을 선택하고, ‘255’이면 그림 4(b)의 가로 방향 도트 패턴 생성을 위한 디더링 행렬을 선택한다. 또는 은닉 영상에서 픽셀 값이 ‘0’이면 그림 4(c)의 서큘러 도트 패턴 생성을 위한 디더링 행렬을 선택하고, ‘255’이면 그림 4(d)의 듀얼 방향 도트 패턴 생성을 위한 디더링 행렬을 선택한다.

◆ 2단계: 선택된 디더링 행렬을 사용해서 하프토닝 과정을 수행한다. 즉, 선택된 디더링 행렬을 입력 영상의 좌측 상단위에 놓고 행렬의 값과 입력 영상의 픽셀 값을 일대일로 비교한다. 이를 통해 입력 영상에서 디더링 행렬 크기만큼 ‘0’ 또는 ‘255’값으로 구성된 군집화 된 도트 패턴을 생성할 수 있다. 그림 5는 디더링 행렬을 사용해서 변환된 군집화 된 도트 패턴의 예시를 보여주고 있다.

Fig. 5.

An example of dot patterns; (a) horizontal dots, (b) vertical dots, (c) circular dots, (d) dual dots

◆ 3단계: 1단계로 다시 돌아가서 은닉 영상에서 다음 픽셀 위치에서 값을 읽어온 후, 디더링 행렬을 선택하고 2단계를 수행한다. 이때 디더링 행렬을 동일한 위치가 아닌, 겹침 없이 디더링 행렬 크기만큼 우측으로 이동하여 하프토닝 과정을 수행한다. 이 과정을 은닉 영상에서 마지막 픽셀 값을 읽을 때까지 반복 수행한다.

그림 6은 가로 및 세로 방향의 도트 패턴으로 구성된 이미지 바코드의 예시를 보여주고 있다. 우측 하단의 빨간 박스는 좌측 상단을 확대한 그림이다. 그림에서 볼 수 있듯이, 가로 방향의 도트 패턴이 존재하는 것을 볼 수 있다. 이는 그림 3(b)의 은닉 데이터의 값이 ‘255’ 즉, 흰색이기 때문에 가로 방향의 도트 패턴이 생성되었다. 물론 다른 영역에서는 세로 방향의 도토 패턴이 존재한다. 그러나 그림 6에서 은닉 영상의 ‘나비’모양이 그대로 노출된 것을 볼 수 있다. 따라서 은닉 영상을 그대로 삽입하는 것이 아니라 은닉 영상의 픽셀 위치를 랜덤하게 재배치할 필요가 있다.

Fig. 6.

Image barcode consisting of horizontal and vertical dot patterns

그림 7은 은닉 데이터의 재배치 과정을 적용한 이미지 바코드의 결과이다.

Fig. 7.

Image barcodes after applying the reordering of the hidden data

그림 6과 비교했을 때, 그림 7(a)에서 은닉 영상의 ‘나비’모양이 사라진 것을 볼 수 있다. 그림 7(b)는 서큘러와 듀얼 도트로 구성된 다른 종류의 이미지 바코드 예시를 보여주고 있다.

3.3 심층 합성곱 신경망의 학습 과정

이미지 바코드에서 은닉된 데이터를 복원하기 위해, 가로 및 세로 방향의 도트 패턴 분류 또는 서큘러 및 듀얼 도트 패턴 분류 과정이 필요하다. 이를 위해 최근 영상 인식 분야에서 큰 각광을 받고 있는 심층 합성곱 신경망을 사용하고자 한다. 심층 합성곱 신경망의 학습 과정은 다음과 같다.

◆ 학습에 사용될 패치 추출: 300장의 그레이 영상을 웹 사이트에서 수집한 후, 3.1절에서 제시한 디더링 기반의 하프토닝 과정을 수집한 영상에 적용해서 하프톤 영상을 획득한다. 그리고 하프톤 영상에서 디더링 행렬 크기만큼 패치를 추출하고, 추출된 패치에 라벨 값을 할당한다. 예를 들어 가로 방향 도트 패턴은 라벨 값 ‘1’을 할당하고, 세로 방향의 도트 패턴은 라벨 값‘0’을 할당한다. 참고로 이 논문에서 사용된 ‘0’을 할당한다. 참고로 이 논문에서 사용된총 패치의 수는 436,956개이다.

◆ 심층 합성곱 신경망의 아키텍처: 그림 8은 이 논문에서 사용된 심층 합성곱 신경망의 아키텍처를 보여주고 있다. 합성곱 신경망은 합성곱(Convolution: Conv) 계층, 배치 정규화(BN, Batch Normalization) 계층, 정류선형유닛(ReLU, Rectified Linear Unit) 계층, 최대 풀링(Max Pooling) 계층, 완전 연결(Fully Connected) 계층, 소프트맥스(Softmax) 계층으로 구성되었다. 이때 사용된 총 레이어의 수는 28개이다.

Fig. 8.

Architecture of the proposed deep convolutional neural networks

◆ 심층 합성곱 신경망의 파라미터 학습: 1단계에서 추출한 패치를 훈련 집합과 검증 집합으로 분류한다. 그리고 훈련 집합을 사용해 심층 합성곱 신경망의 파라미터를 학습한다. 이때 학습에 사용된 최적화 기법은 확률적 경사 하강법(Stochastic Gradient Descent)이다.

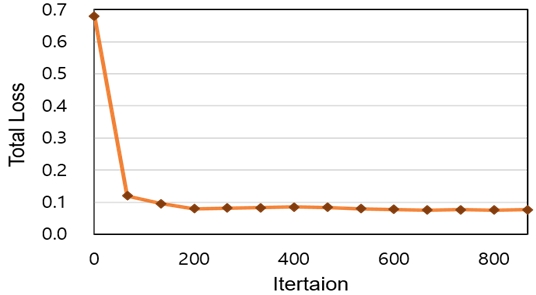
그림 9는 심층 합성곱 신경망의 파라미터 갱신에 따른 손실 함수의 값이 어떻게 변화되는지 그 추이 과정을 보여주고 있다. 그림에서 보듯이, 손실 함수의 값이 감소하다가 수렴되는 것을 볼 수 있으며 이는 역전파(Backpropagation) 과정을 통해 신경망의 파라미터 값이 바르게 갱신되고 있음을 입증해 준다.

Fig. 9.

Change of the total loss, according to the number of parameters updating

3.4 은닉 데이터의 디코딩 과정

심층 합성곱 신경망의 파라미터가 학습이 되면, 이미지 바코드에서 은닉 데이터를 복원할 수 있다. 그림 7과 같은 이미지 바코드가 주어진 경우, 먼저 이미지 바코드에서 래스터 스캐닝(Raster Scanning) 방향으로 디더링 행렬과 동일한 윈도우의 크기에서 패치를 추출한다. 그리고 추출된 패치는 학습된 심층 합성곱 신경망에 입력되고 라벨 값이 추정된다. 그 다음 원도우를 중복되지 않게 래스터 스캐닝 방향을 따라서 이동하면서 상기에 언급된 과정을 반복 수행한다. 이 과정이 완료되면 은닉 데이터를 디코딩할 수 있다. 마지막으로 은닉 데이터의 재배치 과정을 거친 후, 나비 모양을 갖는 은닉 데이터를 완전히 복구할 수 있게 된다.

4.1 실험 환경

성능 비교를 위해 기존의 희소 표현 기반의 디코딩 기법에서 사용된 실험 영상을 사용하였다. 그림 10은 실험 영상으로써, 텍스트, 그림, 로그 등 다양한 영상을 포함하고 있다. 또한 밝기가 균일하거나 아주 밝은 영역을 포함하거나 또는 대비가 높은 영상도 포함되어 있다. 그리고 은닉 데이터는 그림 3에 보이는 나비 영상을 공통으로 사용하였다. 제안한 디코딩 기법의 성능을 평가하기 위해, 기존의 모멘트 기반의 디코딩 기법[4]와 희소 표현 기반의 디코딩 기법[5]를 비교하였다. 그리고 평가 척도로는 원본 은닉 영상의 총 픽셀 수에서 올바르게 추정된 픽셀의 비율을 나타내는 정인식률(Correct Recognition Rates)을 사용하였다.

Fig. 10.

Test images, (a) Text, (b) Butterfly, (c) Hose, (d) Sunflower, (e) Logo, (f) Golf filed

4.2 디지털 이미지 바코드에 대한 실험 결과

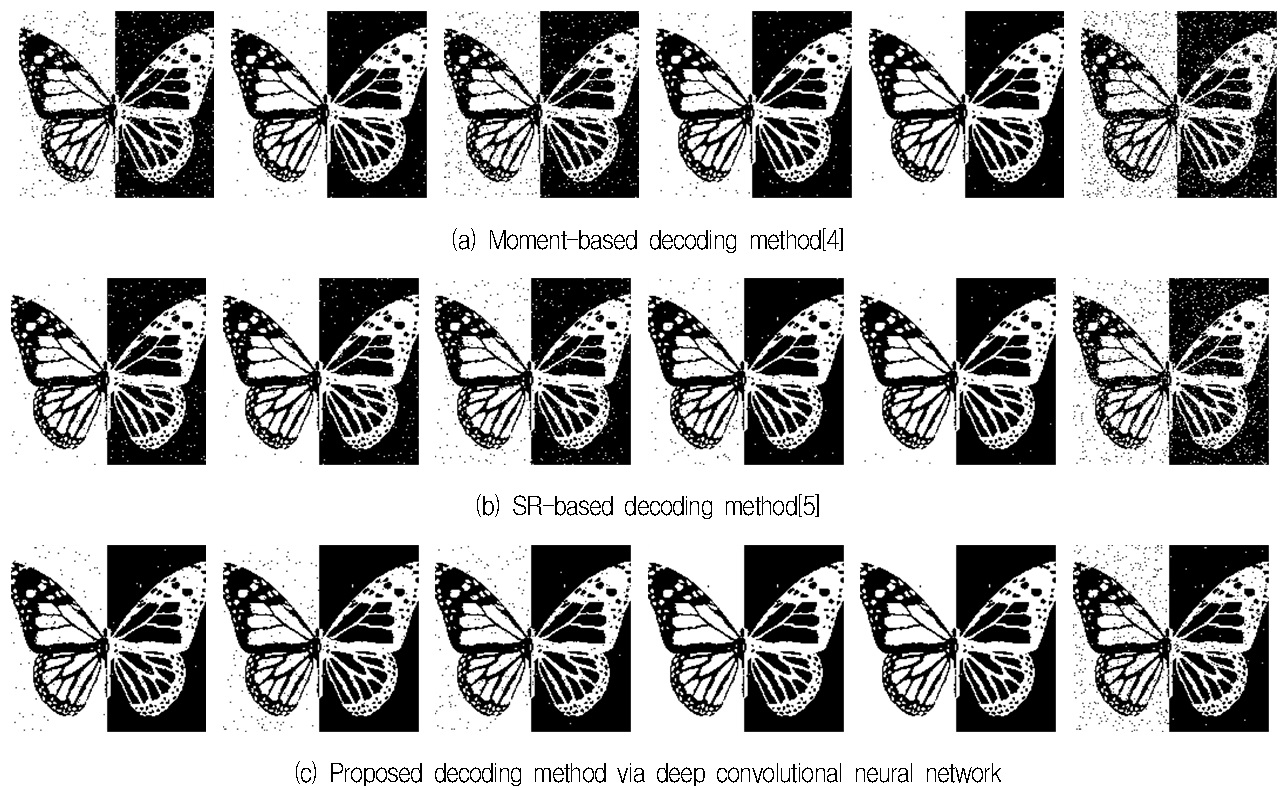
그림 11과 12는 가로 및 세로 방향의 도트 패턴으로 구성된 이미지 바코드와 서큘러 및 듀얼 도트 패턴으로 구성된 이미지 바코드로부터 복구된 은닉 데이터를 보여주고 있다.

Fig. 11.

Experimental results for image barcodes consisting of horizontal and vertical dot patterns

Fig. 12.

Experimental results for image barcodes consisting of circular and dual dot patterns

그림 11과 그림 12에서 각 열은 그림 10의 문자, 나비, 집, 해바라기, 로고, 골프장 영상에 대한 결과이다. 그리고 첫 번째 행은 모멘트 기반의 디코딩 기법, 두 번째 행은 희소 표현 기반의 디코딩 기법, 마지막 행은 제안한 디코딩 기법에 대한 결과이다. 그림 11과 12에서 잡음으로 보이는 점들은 모두 오 분류된 결과이다. 따라서 제안한 기법의 결과가 그림 3의 원본 은닉 영상과 가장 유사한 것을 볼 수 있다. 표 1과 2는 제안한 기법과 기존의 기법에 대한 정인식률의 결과를 보여주고 있다.

Table 1.

Correct recognition rates for the image barcodes consisting of horizontal and vertical dot patterns

Table 2.

Correct recognition rates for the image barcodes consisting of circular and dual dot patterns

제안한 심층 합성곱 신경망 기반의 디코딩 기법의 평균 수치가 기존의 값보다 더 높은 것을 볼 수 있다. 즉 디코딩 기법의 성능이 더 우수하다는 것을 입증한다.

4.3 스캔된 이미지 바코드에 대한 실험 결과

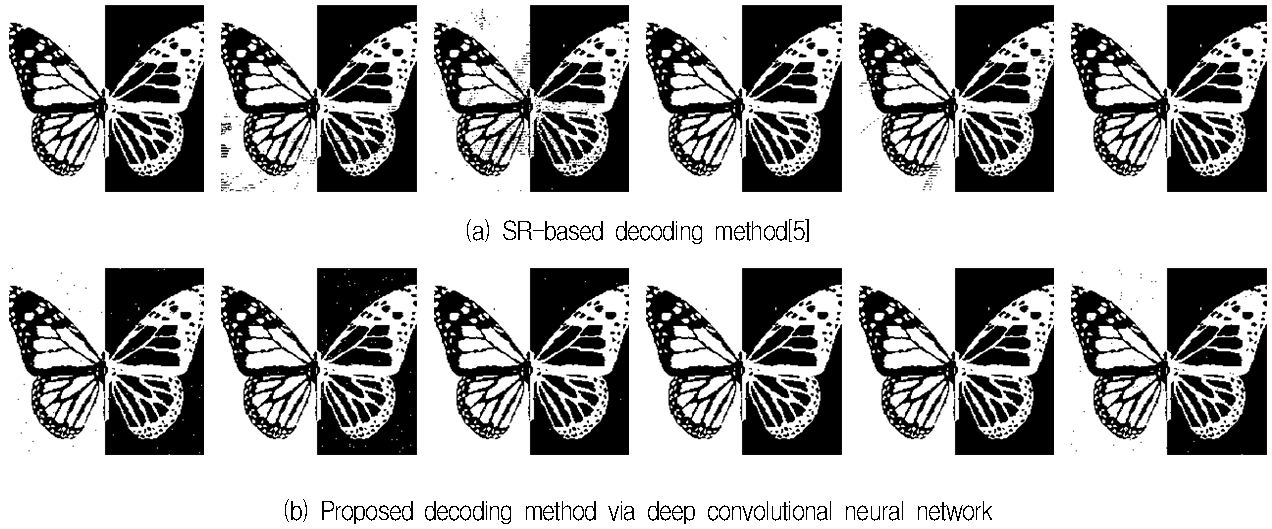
그림 13은 스캔된 이미지 바코드에서 복구된 은닉 영상을 보여주고 있다. 프린팅과 스캐닝 과정이 진행되는 동안 잡음이 추가될 수 있고 무엇보다 픽셀이 찍히는 위치가 미세하게 달라질 수 있다. 이로 인해 실제 스캔된 영상에서 디코딩 기법을 적용할 때, 디코딩 성능이 많이 떨어지게 된다. 표 3은 스캔된 이미지 바코드에 대한 정인식률의 결과를 보여주고 있다. 표에서 보듯이, 실 환경에서도 제안한 기법은 약 96%의 정인식률을 달성할 수 있었다. 반면에 희소 표현 기반의 디코딩 기법이나 모멘트 기반의 디코딩 기법은 약 10%나 성능이 감소된 것을 볼 수 있다.

Fig. 13.

Experimental results for the scanned image barcodes consisting of horizontal and vertical dot patterns

Table 3.

Correct recognition rates for the scanned images barcodes consisting of horizontal and vertical dot patterns

표 4는 기존의 방법과 제안한 기법에 대한 계산처리 시간을 보여주고 있다. 표에서 보듯이, 이미지 바코드에 대한 은닉 데이터 검출 시간은 평균적으로 모멘트 기반의 디코딩 기법은 23초, 희소 표현 기반의 디코딩 기법은 43초, 제안한 심층 합성곱 신경망 기반의 디코딩 기법은 3분 18초가 걸렸다. 실험 환경은 CPU i7-6700 사양에서 동일한 조건에서 비교되었다. 물론 제안한 기법이 정인식률의 측면에서는 가장 높은 결과를 달성했지만, 계산처리 속도에서는 느린 것을 알 수 있다. 이는 패치 기반으로 디코딩 과정이 수행되기 되기 때문이다. 즉 패치마다 매번 심층 합성곱 신경망을 호출하기 때문에 계산처리 시간이 오래 걸리는 것으로 분석된다. 향후에는 이런 제안한 방법의 계산처리 속도를 높이기 위해, 입력 이미지 바코드 영상 전체를 입력으로 받아 은닉 데이터를 복구하는 기법을 개발하고자 한다.

Table 4.

Computational time results for conventional and proposed methods