결합행렬 확장 기법을 이용한 능동위상배열 영상레이다 위상 부호화 코드의 능동반사계수 성능 최적화 연구

Ⅰ. 서 론

위성이나 무인기에 탑재 가능한 영상레이다는 다양한 임무 수행을 위한 여러 종류의 안테나 빔 생성이 요구되어 수백 개의 반도체 송수신 모듈(Transmit Receive Module, T/R 모듈)로 구성된 능동위상배열안테나가 주로 사용된다. 그러나 송수신 모듈의 고장에 의한 영상레이다의 성능저하가 발생할 수 있으므로, 송수신 모듈에 대한 주기적인 정상상태 점검이 필요하다. 현재까지 안테나 특성화를 위한 다양한 기법들이 제시되고 있으며, 대표적인 기법으로 독일 항공연구원(DLR)이 제안하여 TerraSAR–X 위성에 적용된 직교 위상 코드 변조 보정(PCC, Pulse Coded Calibration) 기법이 있다[1]-[4]. 직교 위상 코드 변조 기법은 위상 부호화 코드를 이용하여 실제 운용 환경을 모사하면서 모든 송수신 모듈의 상태를 한 번에 정확하게 진단할 수 있다. 위상 부호화 코드는 코드 고유의 특성, 안테나의 구조 및 특성에 따라 서로 다른 능동반사계수 특성을 보이며, 안테나의 능동반사계수 특성과 송수신 모듈 특성화 정확도에 영향을 미칠 수 있는 주요 요인 중 하나다[5]. 따라서 위상배열안테나의 구조를 기반으로 능동반사계수 특성을 분석하여, 위상 부호화 코드의 종류와 코드 조합을 최적화해야 한다. 이때, 안테나의 결합행렬을 이용하여 실제 안테나 단위에서의 시험 전에 위상 부호화 코드의 최적화가 가능하다.

본 논문에서는 직교 위상 코드 변조 보정 기법을 정의하고, 측정된 결합행렬을 이용하여 직교 위상 코드 변조 보정 기법에 사용되는 대표적인 위상 부호화 코드인 아다마르(Hadamard) 코드의 능동반사계수 특성을 분석하였다. 능동위상배열안테나는 여러 개의 타일로 구성되며, 타일은 16개의 송수신모듈로 구성된다.

측정된 결합행렬은 16개의 송수신 모듈로 구성된 하나의 타일에 대한 결과이며, 모든 안테나 송수신 모듈의 특성화를 위한 위상 부호화 코드의 능동반사계수 특성 분석 및 이를 통한 코드의 최적화 선정을 위해서 하나의 타일에서 측정된 결합행렬을 확장하여 적용하였다. 수백 개의 송수신 모듈로 구성된 안테나 레벨에서의 결합행렬 측정은 가용하지 않기 때문에 하나의 타일에서 측정한 결합행렬을 전체 안테나 레벨로 확장한 결합행렬을 이용하면 전체 안테나 레벨에 적용할 위상 부호화 코드의 능동반사계수 특성을 분석 및 최적화 할 수 있다.

본 논문에서는 결합행렬 확장 기법에 대해 설명하고 확장된 결합행렬을 이용하여 위상 부호화 코드의 능동반사계수 특성을 분석하였으며, 코드 최적화를 수행하였다.

Ⅱ. 직교 위상 코드 변조 보정 기법

안테나 특성화 기법 중 하나인 직교 위상 코드 변조 보정 기법은 직교성을 갖는 위상 부호화 코드를 이용하여 송수신 모듈의 상태 확인과 출력 특성을 점검하는 기법으로 각 송수신 모듈에 해당되는 RF 경로의 특성을 한 번에 정확하게 확인할 수 있다[6].

위상 부호화 코드는 수학적으로 직교성을 갖춘 코드로, 모든 코드들이 직교하고 서로 다른 코드 사이에 상호 상관도가 없는 코드를 말한다. 직교 코드의 종류는 대표적으로 왈시 코드(Walsh Code), 아다마르 코드(Hadamard Code) 그리고 PN 코드(Pseudo-Noise Code) 등이 있으며, 직교 위상 코드 변조 보정 기법에는 아다마르 코드가 일반적으로 사용된다.

직교 위상 코드 변조 보정 기법에 대한 간략한 구조도를 그림 1에 나타내었다.

Fig. 1.

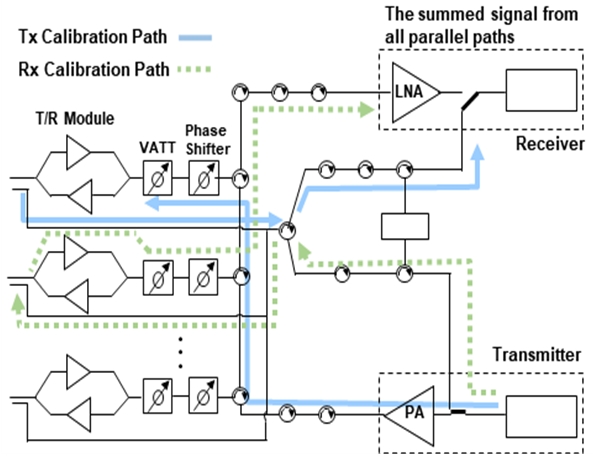
Simplified schematic of active phased array antenna with calibration path using pulse coded calibration

그림 1은 송수신 보정 경로를 포함된 능동위상배열안테나 구조도이며, 각 보정 경로에서의 송수신 모듈의 상태 확인과 출력 특성화를 수행한다. 송신 보정 경로는 송신 보정 신호가 고출력 증폭기(PA, Power Amplifier)가 포함된 RF 분배망을 통하여 각 송수신 모듈에 입력되며, 저잡음 증폭기(LNA, Low Noise Amplifier)를 포함하지 않는 RF 분배망을 지나는 경로이다. 송수신 모듈로 입력된 송신 보정 신호들은 각 위상 변위기를 통해 각 경로에 부여한 독립적인 코드에 따라 0° 또는 180°로 위상 천이된다. 이때 각 경로에 부여되는 독립적인 코드는 직교 위상 코드 변조 보정기법에 사용되는 위상 부호화 코드에 의해 결정된다.

일 예시로 대표적인 위상 부호화 코드인 아다마르 코드 관점에서 수학적인 배경에 의거 설명하면 i번째 송신 보정 신호에서 n 경로의 송신 보정 신호 S(n,i)는 각 경로에 부여한 위상 부호화 코드 M(n,i)와 곱해지며, i번째 누적된 보정 신호 y(n,i)는 식 (1)과 같이 정의된다.

Ⅲ. 위상 부호화 코드의 능동반사계수 특성 분석

위상 부호화 코드의 능동반사계수 분석을 위해 결합행렬과 능동반사계수와의 관계에 대해 3.1장에 간단히 요약하고 결합행렬을 이용하여 분석한 위상 부호화 코드의 능동반사계수 특성 분석을 이어서 설명한다.

3.1 결합행렬과 능동반사계수와의 관계

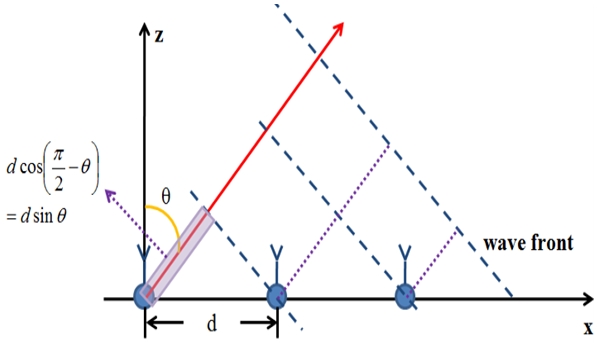
위상 부호화 코드의 능동반사계수 분석을 수행할 능동위상배열안테나는 고각 방향으로 16개의 송수신 모듈로 구성되어 있으며, 전체 안테나를 구성하고 있는 하나의 타일이다. 그림 2와 같은 선형위상배열안테나 구조에서 결합행렬과 능동반사계수와의 관계는 식 (2)와 같이 정의된다[7].

Fig. 2.

Geometry of linear phased array antennas

$\[ {\Gamma }_m\left(\theta \right)=e^{jkmdsin\theta }\sum _{\left(n\right)}{S}_{mn}{e}^{-jkndsin\theta } \]$

(2)

Γ_m(θ)는 m번째 방사소자의 능동반사계수이며, d는 소자 간 간격, S_mn은 결합행렬을 나타낸다.

3.2 위상 부호화 코드의 능동반사계수 특성 분석 결과

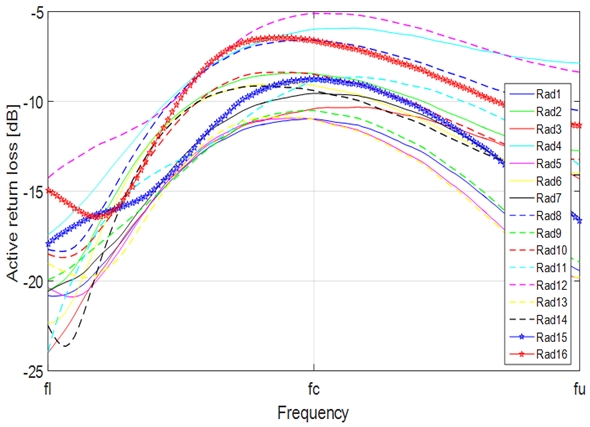
단일 타일에서 측정된 결합행렬을 이용하여 계산한 각 주파수에서의 능동반사계수 특성을 그림 3에 나타내었다. 하단의 송수신 모듈의 번호를 1번, 8번의 송수신 모듈을 중심으로 설정하였다. fc(Center frequency)는 중심주파수에서의 모든 송수신 모듈의 능동반사계수이며, fl(Lower frequency, fc-BW/2)과 fu(Upper frequency, fc+BW/2)는 대역폭(Bandwidth) 기준으로 하한 주파수와 상한 주파수에서의 송수신 모듈에 대한 능동반사계수를 나타낸다.

Fig. 3.

Calculated active return loss of radiators for frequency using measured coupling matrix in one tile

위상 부호화 코드의 길이는 특성화를 수행할 송수신 모듈 개수 N에 의해 결정되며, 최소 송수신 모듈 개수 N≤2^k (k=정수)로 결정된다. 16개의 송수신 모듈 특성화를 위해 길이가 16인 아다마르 코드를 선정하였으며, 각 송수신 모듈에 아다마르 코드의 각 열이 적용되었을 때 능동반사계수 특성을 분석하였다. 아다마르 코드의 12번째 열의 코드가 안테나 송수신 모듈에 적용되었을 때 최대능동반사계수 특성이 나타났으며, 12번째 송수신 모듈에서 –5.09dB로 나타났다. 최대능동반사계수란 16개의 모든 코드를 각 송수신 모듈에 적용했을 때 특정 코드에서의 최대능동반사계수를 나타내며, 그림 4에 아다마르 코드 12번째 열을 적용하였을 때 16개 송수신 모듈의 능동반사계수 특성을 나타냈다[8].

Fig. 4.

Active return loss of all radiators when row 12 of Hadamard code is applied

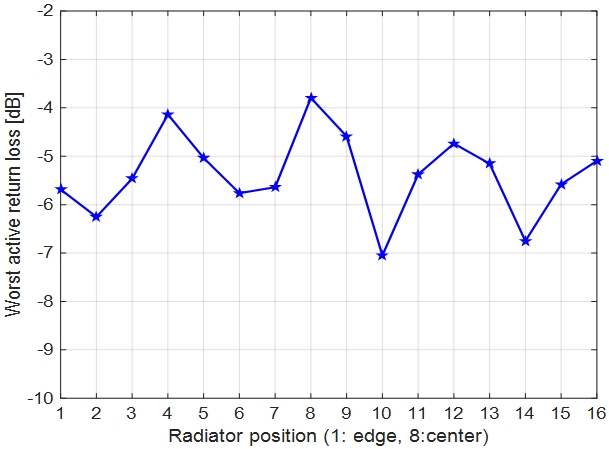
그림 5는 길이가 16인 아다마르 코드가 모든 송수신 모듈에 적용되었을 때 각 송수신 모듈에서의 최대능동반사계수 특성을 나타낸다. 그림 4는 아다마르 코드의 하나의 열을 16개 송수신 모듈에 적용하여 얻어진 각 송수신 모듈의 능동반사계수, 그림 5는 모든 코드를 각 송수신 모듈에 적용하였을 때 각 송수신모듈에서의 최대능동반사계수이다.

Fig. 5.

Worst active return loss of each radiator

위상 부호화 코드를 적용했을 경우 능동반사계수 성능이 저하되는 것을 확인할 수 있으며 이는 위상 부호화 코드 성분에 따라 일부 송수신 모듈의 위상이 180° 천이되어 송수신 모듈 간의 결합계수가 변화되었기 때문이다.

Ⅳ. 확장된 결합행렬을 이용한 위상 부호화 코드 능동반사계수 특성 분석

위상 부호화 코드 최적화의 일환으로 하나의 타일 송수신 모듈의 특성화를 위해 길이가 16인 아다마르 코드로도 가능하지만 신호 대 잡음비(Signal-to-Noise Ratio) 특성을 고려하여 길이가 32, 64 또는 N(N=2^k, k=정수)개의 아다마르 코드를 선택할 수 있다. 이런 경우 송수신 모듈 16개를 특성화하기 위해 N개의 코드 중 16개 코드 성분을 선택하여 행과 열의 길이가 N×16으로 구성된 코드를 생성하고 길이가 16인 결합행렬을 이용하여 상대적으로 더 좋은 능동반사계수 특성을 보이는 16개의 코드 조합을 찾을 수 있다[9].

안테나 레벨의 구조에 적용할 위상 부호화 코드 또는 서로 다른 코드들을 조합하여 길이가 16인 결합행렬 측정 데이터를 이용하여 능동반사계수 특성 분석이 어려운 경우에는 타일 레벨처럼 하위 레벨의 안테나 구조에서 측정한 결합행렬을 확장하여 능동반사계수 특성을 사전에 분석하고 최종적으로 사용할 코드를 선정할 수 있다. 특히 안테나 레벨에서의 결합행렬 측정은 어렵기 때문에 하위 레벨인 타일레벨에서 측정한 결합행렬 데이터를 이용하여 상위 레벨에 적용할 위상 부호화 코드를 분석하여 최적의 코드를 선정하여야 한다.

안테나 레벨의 결합행렬을 손쉽게 확장하는 방법을 4.1장에서 설명하고 확장된 결합행렬을 이용한 안테나 레벨에 적합한 위상 부호화 코드의 능동반사계수 특성 분석 및 최적화 결과를 이어서 설명한다.

4.1 결합행렬의 확장

본 장에서는 제한된 길이의 결합행렬을 이용하여 확장된 안테나 구조에 적용할 위상 부호화 코드의 능동반사계수 특성을 분석하는 방법을 설명한다.

안테나 특성화를 수행할 능동위상배열안테나의 방위각 방향의 결합계수는 상대적으로 무시할 만큼 작기 때문에, 결합행렬을 코드 길이를 반영하여 고각 방향으로 송수신 모듈 개수를 최대 48개로 확장하였으며 확장시킨 결합행렬을 이용하여 능동반사계수 특성을 분석하였다. 다수의 송수신 모듈 그룹으로 구성되는 실제 안테나 구조에서는 측정한 결합행렬 데이터를 이용하여 위상 부호화 코드의 능동반사계수 특성을 최적화하기 어렵기 때문에 타일 단위에서 획득한 측정 데이터를 이용하여 안테나 레벨에 적용할 수 있는 위상 부호화 코드의 특성을 사전에 분석하고 코드 최적화에 활용할 수 있다.

다음과 같은 사항을 고려하여 제한된 길이의 결합행렬을 특정 길이의 위상 부호화 코드에 적합하게 고각 방향으로 확장할 수 있다.

• 방사 소자 간 결합계수(Coupling Factor)는 소자간 거리가 멀어짐에 따라 감소하며 일정 거리가 떨어진 방사 소자 간 결합계수는 무시할 만큼 작다.

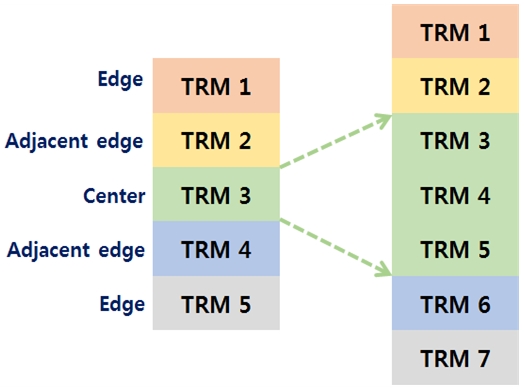
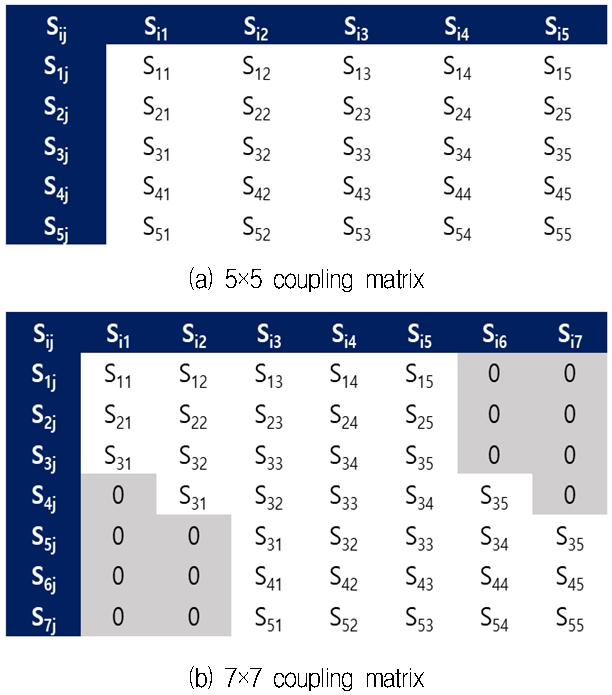
• 배열 가장자리에 위치한 방사 소자는 특유한 결합계수 특성을 갖지만 배열 중심에 위치한 방사 소자들의 결합계수 특성은 유사하다. 즉, 배열 위치에 따른 방사 소자의 결합계수 특성을 고려하여 그림 6과 같이 5개의 송수신 모듈로 구성된 선형위상배열안테나의 결합행렬을 이용하여 7개의 송수신 모듈로 구성된 선형위상배열안테나의 결합행렬을 생성할 수 있다.

Fig. 6.

Approach of extending coupling matrix in linear phased array antennas

그림 7은 앞에서 설명한 결합행렬 확장 기법을 이용하여 길이가 5인 결합행렬을 길이가 7인 결합행렬로 확장한 하나의 예를 나타낸 것이다. 길이가 7인 결합행렬의 회색 음영 부분은 방사 소자 간 결합계수가 무시할 만큼 작아 0으로 가정한 부분이다.

Fig. 7.

In an example extended coupling matrix from 5×5 coupling matrix

송수신 모듈 16개에 대한 결합행렬 데이터를 본 논문에서 제시한 결합행렬 확장 기법을 적용하여 고각 방향으로 송수신 모듈이 48개인 안테나의 결합행렬 데이터로 확장하였다.

본 논문에서 제안한 결합행렬 확장 기법에 대한 유효성을 검증하기 위하여 확장된 결합행렬 성분 중 결합계수가 0으로 가정된 크기/위상 성분을 외삽법(Extrapolation)을 이용하여 0이 아닌 유효한 값으로 가정하였고, 두 결합행렬을 이용하여 계산한 저주파수 대역에서의 방사소자 위치에 따른 능동반사계수 특성을 비교 분석하였다. 외삽법을 적용하기 위하여 결합행렬의 크기성분은 방사소자 간 거리를 고려하여 방사소자 간 1.75dB 감쇠로 설정하였고 위상 성분은 길이가 16인 결합행렬 데이터에 기반을 두어 설정하였다.

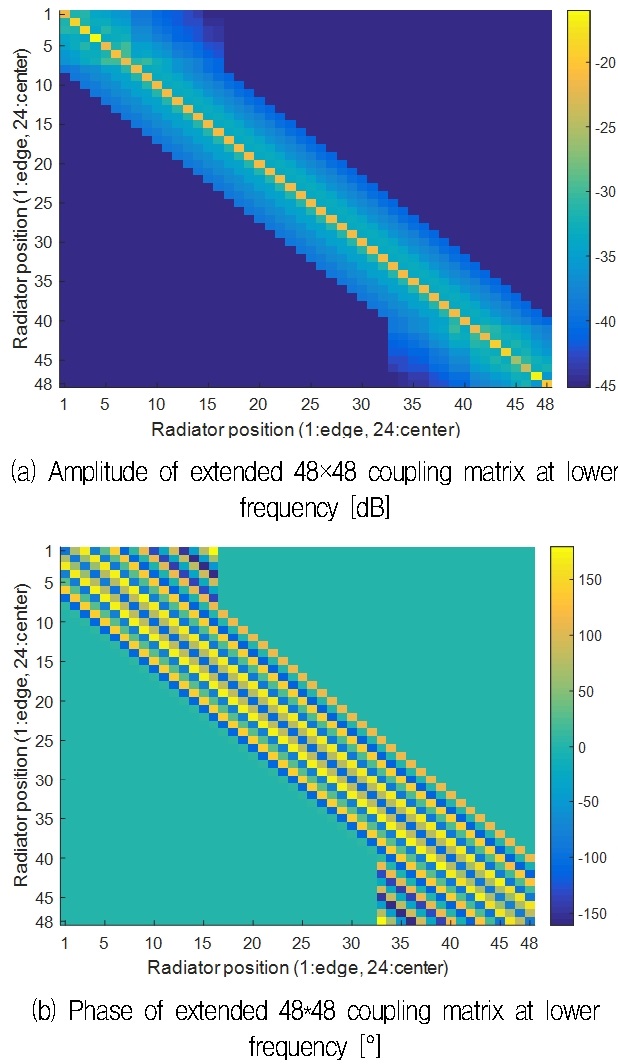
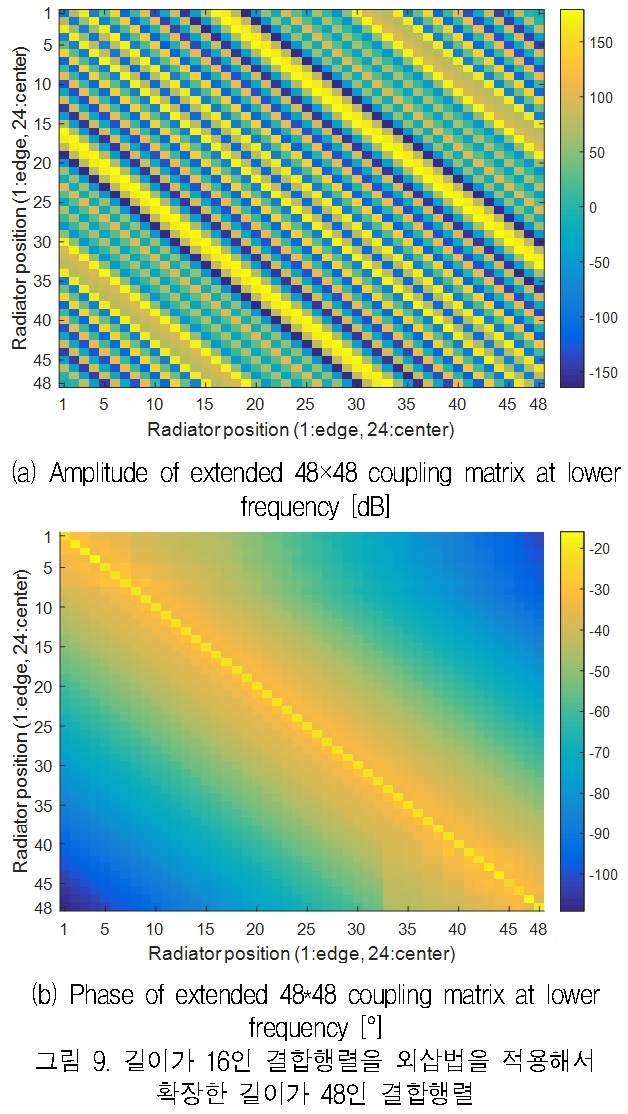
그림 8에 그림 7에서 제시한 결합행렬 확장 기법을 적용하여 길이가 16인 결합행렬을 저주파에서 길이가 48인 결합행렬로 확장한 결과를 나타내었으며, 그림 9에는 저주파수에서의 외삽법을 적용하여 확장한 결합행렬을 나타내었다.

Fig. 8.

48×48 coupling matrix extended from 16×16 coupling matrix

Fig. 9.

48×48 coupling matrix extended from 16×16 coupling matrix with extrapolation

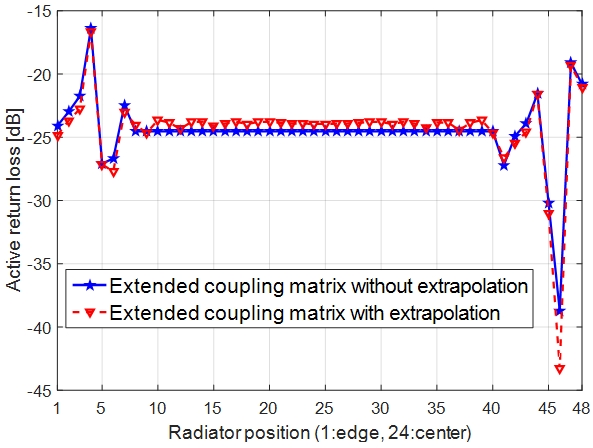
그림 10에는 본 논문에서 제안한 결합행렬 확장 기법을 이용하여 확장한 결합행렬에 대한 능동반사계수 특성과 외삽법을 적용하여 확장한 결합행렬의 능동반사계수 특성 비교 결과를 나타내었다.

Fig. 10.

Comparison of active return loss at lower frequency

두 결과는 거의 비슷한 결과를 보임을 확인할 수 있으며 외삽법 과정 없이 본 논문에서 제시한 결합행렬 확장 기법을 이용하더라도 위상 부호화 코드의 능동반사계수 특성을 확인 및 예측할 수 있을 것으로 판단된다.

4.2 확장된 결합행렬을 이용한 위상 부호화 코드 능동반사계수 특성 분석

본 논문에서 제안한 결합행렬 확장 기법을 이용하여 고각 방향으로 48개의 송수신 모듈로 구성되도록 확장한 결합행렬을 이용하여 송수신 모듈 48개에 적합한 아다마르 코드의 능동반사계수 특성을 분석하였다.

아다마르 코드의 길이는 송수신 모듈 48개를 특성화하기 위한 최소 길이인 64로 설정하였다. 길이가 64인 아다마르 코드는 64개의 행과 열로 구성되어 64개의 코드를 조합하여 다양한 조합의 코드를 생성할 수 있다. 송수신 모듈 48개를 특성화하기 위해서는 행과 열의 길이가 64×48로 구성된 코드를 생성해야 하며 다양한 코드 조합에 따라 생성된 코드는 서로 다른 능동반사계수 특성을 갖기 때문에 능동반사계수 특성이 개선되는 코드를 선정해야 한다.

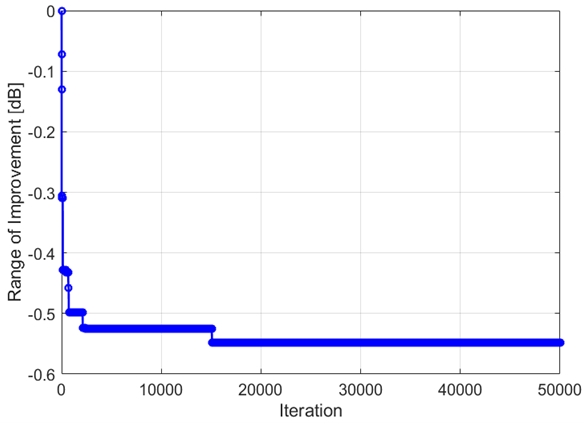
반복 시뮬레이션을 통해 64개의 코드 성분 중 48개를 임의로 선택하여 코드의 최대능동반사계수 특성이 개선되는 코드 조합을 찾기 위한 시뮬레이션을 수행하였으며 그림 11에 해당 결과를 나타내었다. 시뮬레이션을 통해 얻어진 코드의 최대능동반사계수의 개선 여부를 확인하기 위해 초기 코드의 최대능동반사계수 값은 길이가 16인 아다마르 코드의 최대능동반사계수 값(-3.79dB)으로 설정하였다. 따라서 시뮬레이션에 의해 생성된 코드의 최대능동반사계수와 초기 코드의 최대능동반사계수를 비교하여 가장 좋은 특성을 보이는 코드를 확인하였으며 능동반사계수 개선 값을 그림 11의 y축에 나타내었다.

Fig. 11.

Simulation results to find code sequence with improved their active return loss performance

시뮬레이션 반복횟수가 많아짐에 따라 상대적으로 최대능동반사계수 특성이 개선됨을 확인할 수 있으며 길이가 16인 아다마르 코드의 최대능동반사계수 특성과 비교하여 약 0.6dB 개선되는 코드를 얻었다. 최대능동반사계수 특성이 개선된 코드는 향후 안테나 레벨에서의 알고리즘 검증시험을 통해 알고리즘 정확도 개선 여부를 확인할 예정이다.

Ⅴ. 결론 및 향후 과제

능동위상배열 영상레이다 적용을 위한 위상부호화 코드의 능동반사계수 특성 분석은 송수신 모듈 특성화 알고리즘 개발에서 필수적은 요소로서 안테나 능동반사계수 특성에 직접적인 영향을 줄 수 있다.

본 논문에서는 고각 방향으로 16개의 송수신 모듈로 구성된 타일에서 측정한 결합행렬을 이용하여 송수신 모듈 특성화 알고리즘에 사용되는 위상 부호화 코드의 능동반사계수 특성 분석에 대해 기술하였다.

다수의 타일을 확장한 안테나를 구성하는 다수 개의 송수신 모듈의 특성화에 필요한 위상 부호화 코드의 능동반사계수 특성 분석을 위해 제한된 길이의 결합행렬을 확장하는 방법을 제시하였으며 확장된 결합행렬을 이용하여 능동반사계수 특성을 고려한 위상 부호화 코드의 최적화 구현 방안을 확인하였다.

본 논문에서 제시한 결합행렬 확장 기법의 장점은 다음과 같다. 타일 레벨에서의 결합행렬 측정결과에 안테나 소자의 물리적인 특성이 반영되어 있으므로 다양한 코드 조합에 따른 코드의 능동반사계수 특성 변화 추이는 동일할 것으로 예상되며, 본 논문의 확장 결합행렬과 측정한 결합행렬 간의 오차는 미비할 것으로 예측된다. 또한 전체 안테나 레벨에서의 결합행렬 측정은 용이하지 않기 때문에 단일 타일에서의 측정 결과를 활용하는 결합행렬 확장 기법을 적용하여 안테나 레벨에서의 분석을 수행하는 것이 효율적이다.

확장된 결합행렬을 이용하여 능동반사계수 특성이 개선되는 코드를 찾기 위해 반복 시뮬레이션을 통해 길이가 16인 아다마르의 최대능동반사계수 특성 대비 약 0.6dB 개선되는 코드 조합을 확인하였으며, 더 나아가 능동반사계수 특성이 개선된 코드의 알고리즘 정확도 개선 여부를 향후 안테나 레벨에서의 알고리즘 검증시험을 통해 확인할 예정이다.

본 논문에서 제안한 결합행렬 확장 기법과 능동반사계수 특성을 고려한 위상부호화 코드 선정 방법은 추후 다수의 송수신 모듈로 구성된 안테나에 적용하여 안테나 단위에서의 코드 결정과 송수신 모듈 점검 기법의 정확도 향상에 활용할 계획이다.

References

• D. Hounam, M. Schwerdt, and M. Zink, "Active Antenna Module Characterisation by Pseudo-Noise Gating", In 25th ESA Antenna Workshop on Satellite Antenna Technology, Noordwijk, Netherlands, (2002).
• B. Brautigam, M. Schwerdt, and M. Bachmann, "Individual T/R module characterisation of the TerraSAR-X active phased array antenna by calibration pulse sequences with orthogonal codes", in Proc. IGARSS, p5202-5205, Jul), (2007. [https://doi.org/10.1109/igarss.2007.4424034]
• B. Brautigam, M. Schwerdt, and M. Bachmann, "An efficient method for performing monitoring of active phased array antennas", IEEE Trans. Geosci. Remote. Sens, 47(4), p1236-1243, Apr.), (2009.
• E. Schied, F. Rostan, A. Ostergaard, I. N. Traver, and P. Snoeij, "The Sentinel-1 C-SAR internal calibration", in Proc. 8th EUSAR, Aachen, Germany, p1-3, Jun., 7-10), (2010.
• A. Ostergaard, I. Navas-Traver, P. Snoeij, E. Schied, F. Rostan, and R. Croci, "Pulse coded calibration of the Sentinel-1 SAR Phases array antenna optimized for low active return loss", in Proc. IET Int. Conf. Radar, Glasgow, p1-4, Oct.), (2012. [https://doi.org/10.1049/cp.2012.1659]
• J. D. Lee, S. Y. Kim, J. B. Sung, D. W. Yi, and C. H. Nam, "A Study on Technique for T/R Module Monitoring of Active Phased Array Antennas", KIMST Annual Conference Proceedings, p1021-1022, Nov.), (2015.
• D. M. Pozar, "The Active Element Pattern", IEEE Trans. Antennas Propagat, 42(8), p1176-1178, Aug.), (1994. [https://doi.org/10.1109/8.310010]
• J. D. Lee, S. Y. Kim, J. B. Sung, D. W. Yi, and C. H. Nam, "An Analysis for Active Return Loss of Phase Encoding Code", KIMST Annual Conference Proceedings, p713-714, Nov.), (2016.
• J. D. Lee, J. B. Sung, D. W. Yi, and S. Y. Kim, "A Study on Improvement of Active Return Loss of Phase Encoding for Spaceborne Active Phased Array SAR", KIMST Annual Conference Proceedings, p1291-1292, Nov.), (2018.