난류 모델에 따른 다운윈드형 풍력터빈 발전 성능 예측
초록
신재생 에너지 자원 중 풍력은 투자 대비 전력 생산량이 높으며, 유해 배출물이 없다는 점에서 가장 유망한 에너지 자원 중 하나이다. 최근 주거용 발전 에너지의 관심이 많아 본 연구에서는 300W급 다운윈드형 소형 풍력터빈을 개발하고자 한다. 풍속 10㎧에서 300W 발전이 가능한 블레이드를 설계하고, 풍력터빈의 발전 성능검증을 위하여 ANSYS CFX를 사용하여 유동해석을 하였다. k-ε, k-ω, SST 난류 모델에 따라 블레이드에서의 토크 변화를 확인하였다. 블레이드 회전 속도와 산출된 토크로부터 기계적인 출력을 계산하였다. 난류 모델에 따른 토크, 출력, 주속비(λ)와 출력계수(Cp)에 대한 값을 확인하였다. 최대 토크와 출력, 출력계수는 k-ε, k-ω, SST 순으로 나타났으며, 3가지 난류 모델 모두에서 10㎧에서 300W급 성능을 검증하였다. k-ε은 주속비 5.860에서 출력계수 0.267, k-ω는 주속비 5.933에서 0.259, SST는 주속비 6.347에서 0.258을 확인하였다.
Abstract
Wind power is one of the most promising energy resources among renewable energy resources in terms of high power output relative to investment and no toxic emissions. Recently, there is a lot of interest in residential power generation and we would like to develop a 300W class small wind turbine with a downwind type in this study. A blade capable of 300W generation at a wind speed of 10m/s was designed and then numerical analysis is performed using ANSYS CFX to verify the generation performance of the wind turbine. Torque change in blades was confirmed by turbulence model k-ε, k-ω, SST. The mechanical output was calculated from the blade rotation speed and the calculated torque. The values of torque and power for wind speed and the coefficient of power(Cp) value for tip speed ratio(TSR) according to the turbulence were confirmed. The maximum torque, power and Cp were in the order of k-ε, k-ω, and SST and all three turbulence models were identified as capable of 300W generation at 10m/s. k-ε is checked for Cp values of 0.267 for TSR of 5.860, k-ω is 0.259 for TSR of 5.933, SST is 0.258 for TSR 6.347.
Keywords:
small wind turbine, horizontal axis wind turbine, downwind, CFD, turbulence modelⅠ. 서 론
이산화탄소(CO2) 등에 의한 온실 가스 증가로 인하여 지구 온난화와 기후 변화는 인류의 미래를 위협하고 있으며, 이러한 문제 해결을 위해서는 재생 가능한 에너지의 개발이 시급하다. 몇몇 신재생 에너지 자원 중 풍력은 투자 대비 전력 생산량이 높으며, 유해 배출물이 없다는 점에서 태양광과 함께 가장 유망한 에너지 자원 중 하나이다. 바람의 힘을 이용하여 발전하는 풍력터빈은 회전축에 따라 구분되며, 보다 일반적인 수평축 풍력터빈은 주로 상업용으로 지난 20여 년간 꾸준히 개발되어 최대 6 MW의 출력을 낼 수 있다. 최근 들어 주택가 등 도심을 중심으로 소형 풍력터빈의 수요가 요구됨에 따라 이에 대한 관심이 증가하고 있다.
소형 풍력터빈은 바람의 세기나 방향이 위치와 시간에 따라 민감하게 변하는 특성으로 전력량이 적정 출력을 초과하거나 감소하는 다변화 환경 속에서 최상의 성능을 유지하기 위한 연구들이 활발히 진행되고 있다. Messineo 등은 소형 풍력터빈은 대형 풍력에 비해 크게 주목받지 못하고 있으나, 바람 상태 및 지형 유형과 밀접하게 관련되어 있음을 보여주었다[1]. Ernesto 등은 도시 지역에서 최대로 발전 효율을 높이기 위하여 전산유체역학을 활용한 소형 풍력터빈의 최적 배치 방법론을 제시하였다[2]. Keith 등은 도심 환경에서 소형 풍력터빈의 생산성 향상을 위하여 주변 지형과 배치, 난류에 대한 조사가 필요하며, 평균 풍속 측정, 확률 분포에 의한 시뮬레이션을 통하여 출력을 예측하고 있다[3].
항력을 활용한 수직축 풍력터빈의 발전 성능을 예측하기 위하여 Kim 등은 터빈 날개의 개수와 터빈 내부 바람의 관통 경로 유무에 따른 유동해석을 수행하였으며[4], Lee 등은 시뮬레이션을 통해 V형태의 주날개와 보조날개의 매수를 변경하여 최적의 효율과 출력을 확인하였다[5]. 양력을 이용한 수평축 풍력터빈은 보편적으로 타워의 전면부에 블레이드가 위치한 업윈드(Upwind) 형식과 최근 소형화에 따른 타워 후면부에 방향날개를 대신하여 블레이드가 요제어 기능을 병행하는 다운윈드(Downwind) 타입으로 구분된다. Mo 등은 수평축 풍력터빈 블레이드를 설계하여 목표 출력을 검증하였으며[6], Choi 등은 풍속에 따라 다운윈드 풍력터빈 블레이드의 구조적 특성을 분석하였다[7].
국내에서는 앞서 제시한 연구들을 포함하여 주로 풍력터빈 블레이드에 한정되어 수치해석을 이용한 성능 예측을 수행하였으나 기어박스, 발전기, 제어부 등을 보호하는 너셀(Nacelle), 타워(Tower) 등 주변 요소들이 블레이드에 미치는 간섭에 대한 연구는 미진한 상태이다.
풍력터빈 전체 시스템에 대한 3차원 시뮬레이션을 위해서는 고성능 컴퓨터와 많은 계산 시간이 요구된다. 또한 상호 간섭 등 전체 시스템에 작용하는 공기의 흐름이 어떻게 형성되는가에 따라 풍력터빈의 성능 예측이 좌우되어 해석 정확도를 높이기 위해서는 타당한 난류 모델의 선택이 시뮬레이션의 중요한 측면 중 하나이다.
본 연구에서는 다운윈드 형식의 300W급 소형 풍력터빈 개발을 위하여 3차원 형상에 대한 개념설계와 k - ϵ, k - ω, SST(Shear Stress Transport) 난류 모델에 대한 성능 분석을 통해 풍력터빈에서의 발전 성능을 예측하였다.
Ⅱ. 풍력터빈 설계 및 유동해석
2.1 풍력터빈 형상 설계
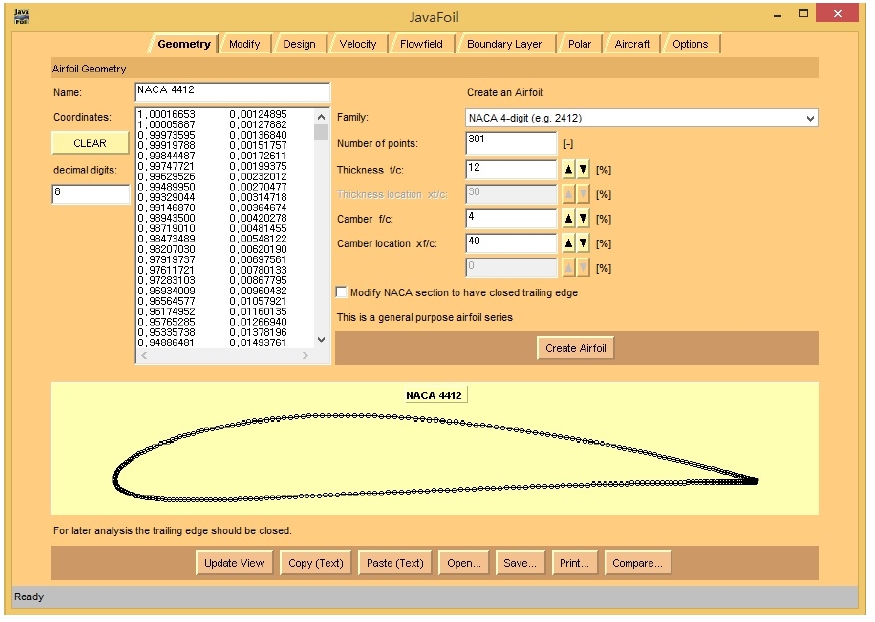
풍력터빈에 사용되는 블레이드 제작을 위하여 개념설계를 수행하였다. 에어포일에 필요한 데이터를 범용 소프트웨어인 Javafoil에서 산출하였다. 그림 1은 NACA 4412 지오메트리 값을 계산하는 과정을 보여준다. 저속에서 고양력의 특성을 갖는 NACA 4계열(NACA 4-digit)을 선택하고, 두께(Thickness t/c)에 대한 정보와 챔버(Camber f/c)와 챔버 위치(Camber Location xf/c)에 대한 정보를 입력하였으며, 동일 방법으로 NACA 6415, NACA 6418에 대한 형상 데이터를 추출하여 CAD 데이터에 활용하였다.
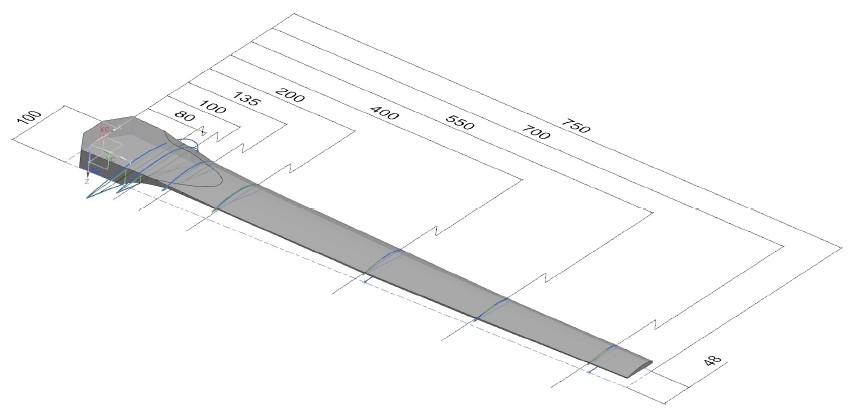
그림 2는 본 논문에 적용된 블레이드의 3차원 형상을 나타내었다. 블레이드 전체 길이는 750㎜이며, 블레이드 끝단부인 550~750㎜구간은 NACA 4412, 중심부인 200~550㎜구간은 NACA 6415, 블레이드의 가장 두꺼운 부분인 200㎜까지는 NACA 6418을 적용하여 에어포일 형상이 변하는 불연속면은 보간법을 이용하였다. CAD 프로그램은 상용 소프트웨어인 지멘스사의 NX를 이용하여 설계하였다.
그림 3은 풍속 10㎧에서 300W급 발전이 가능한 다운윈드 형식의 수평형 풍력터빈을 설계하였다. 너셀(Nacelle) 내부에는 요제어가 가능한 시스템을 포함한 발전기가 위치하며, 발전기의 로터 부분에 블레이드를 조립하는 구조로 타워에 고정되어 있다. 바람에 따라 시계방향으로 회전하는 다운윈드형 풍력터빈으로 블레이드를 조립한 전체 직경은 1,550㎜이다. 공력해석을 위하여 블레이드 중심부의 높이는 직경의 4배로 설계하였다.
2.2 유동해석 조건
앞서 지멘스사의 NX에서 설계한 형상 데이터를 이용하여 공기 흐름에 영향이 있는 영역을 2개의 유동장으로 나누어 해석 프로그램인 ANSYS CFX로 계산하였다.
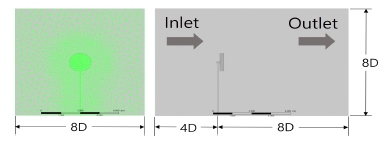
그림 4는 전체 유동장의 전면부와 측면부의 모습을 보여주고 있다. 블레이드 형상을 제외한 실린더 모양의 회전하는 영역과 입구 및 출구, 지면 조건이 존재하는 타워와 너셀 형상을 제외한 전체 유동장으로 구분된다.
풍력터빈의 블레이드는 바람의 진행 방향에서 타워 후방에 위치하는 다운윈드 형식이다. 입구와 출구의 가로 세로 비율은 직경의 8배이며, 블레이드의 중심부는 입구 사각형의 중앙에 위치하고 있다. 타워의 중심부에서 입구까지 블레이드 직경의 4배이고, 타워에서 출구까지의 거리는 직경의 8배이다.
블레이드의 회전 영역을 포함한 너셀과 타워 주위의 격자 크기는 벽면으로부터 점성효과를 고려하여 해석 툴의 Inflation 옵션을 이용하는 등 전체 영역에 비해 매우 조밀하게 격자 품질을 향상시켰다. 회전 영역의 절점(Node)는 약 1,800,000개, 요소(Element)는 6,000,000개이다. 회전 영역을 제외한 해석 영역의 절점은 1,000,000개, 요소는 4,500,000개로 전체 해석 영역의 요소는 약 10,500,000개로 사면체와 육면체 격자로 혼합하여 구성하였다.
경계조건으로는 입구 경계면에서 10㎧의 균일 속도로 정의하고, 출구의 경우 경계면의 압력 손실이 없다고 가정하여 0㎩로 설정하였다. 블레이드, 너셀, 타워 그리고 지면은 점성 유동으로 벽면(No-slip) 조건으로 정의하였다. 회전 영역과 접하는 경계 영역에 대해서는 주기적으로 연결되는 조건에서 사용할 수 있는 GGI(General Grid Interface)를 적용하여 해석을 수행하였다. 또한 전체 유동장의 풍속이 10㎧일 때 블레이드의 회전속도는 50, 150, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1100rpm의 각속도 조건을 적용하였다.
2.3 난류 모델
풍력터빈의 발전 성능에 대하여 보다 정확한 예측을 위해서는 전산유체역학(CFD)를 이용한 공력 특성 결과의 높은 신뢰성이 요구된다. ANSYS 등 범용으로 채택하고 있는 여러 난류 모델 중 타당한 난류 모델을 선정하는 것은 개발 과정에서 소요되는 많은 시간을 절감할 수 있다.
일반적으로 가장 넓은 분야에서 다양하게 사용되는 k - ϵ 난류모델은 강건(Robust)하고 타당한 정확도를 갖으나 큰 압력구배나 강한 박리를 갖는 유동에서는 사용하기가 부적합하며, k - ω 난류모델은 낮은 레이놀즈수에서 강건하고 역 압력구배에서 향상된 성능을 보이나 자유류(Free Stream Condition)에서 민감하다고 알려져 있다. 이 두 모델의 단점을 보완한 Menter의 SST 난류 모델은 다른 두 모델에 비하여 많은 계산시간으로 설계 과정에서 많은 비용이 소요된다[8].
난류 모델은 다양하고 복잡한 유동 구조 모두를 만족하는 모델이 없기 때문에 본 연구에서 k - ϵ, k - ω, SST 난류 모델에 대하여 각각 얼마나 공력 특성이 다른지 확인하고자 한다.
2.4 유동해석 결과
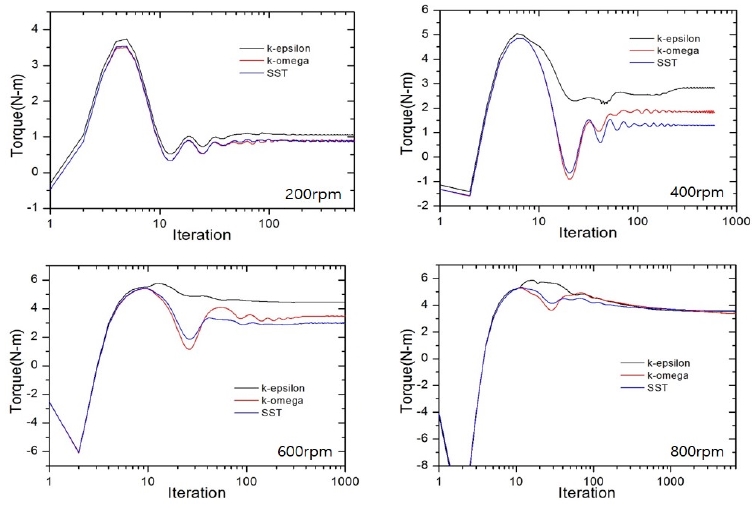
그림 5는 수치계산에서 회전속도 별 반복횟수에 따라 풍력터빈의 토크값이 수렴되고 있는 과정을 로그 스케일을 적용하여 도시하였다. 회전속도가 증가함에 따라 반복횟수가 증가하며, 계산 시간이 더 소요됨을 확인할 수 있다.
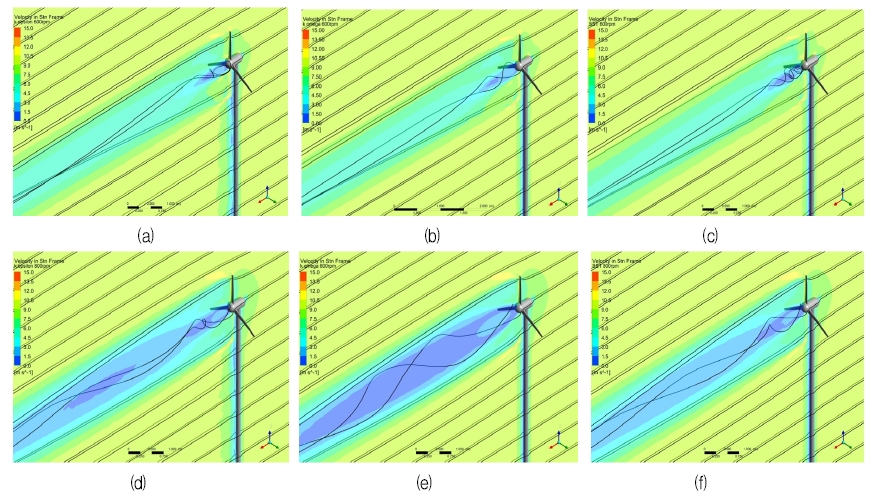
그림 6은 난류 모델에 따라 수직 중심면의 속도분포와 유선(Streamline)을 도시하였다. (a) ~ (c)는 블레이드 회전속도 600rpm에서 (a)는 k - ϵ, (b)는 k - ω, (c)는 SST 조건을 보여준다. (d) ~ (f)는 블레이드 회전속도가 800rpm으로 (d)는 k - ϵ, (e)는 k - ω, (f)는 SST이다. 표 1의 결과로부터 600rpm의 토크값은 k - ϵ > k - ω > SST 순서이고, 800rpm에서는 SST > k - ϵ > k - ω 순서이다. 그림 6과 비교하여 수직 중심면을 기준으로 속도가 낮은 파란색 부분이 넓게 분포된 경우가 토크값이 낮음을 확인할 수 있다. 블레이드에 영향을 주는 토크값이 후류 속도에 영향을 미치는 것을 예측할 수 있다.
Ⅲ. 풍력터빈 성능 분석
풍력터빈의 발전 성능을 예측하기 위해서는 식 (1), (2)와 같이 블레이드에 작용하는 풍압(p)과 면의 수직벡터() 그리고 축간 거리()를 이용하여 CFX에서 터빈에 작용되는 토크(T)와 블레이드의 회전속도(ω)를 곱하여 계산할 수 있다[4].
| (1) |
| (2) |
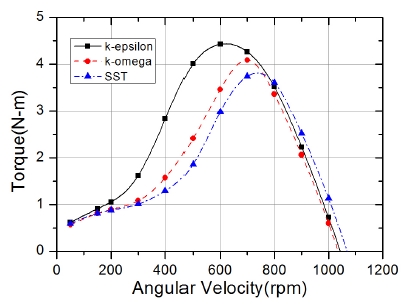
표 1은 유동해석에 의해 계산된 난류 모델에 따른 토크값에 대한 결과를 보여주고 있다. 그림 7과 그림 8은 난류 모델에 따라 블레이드 회전속도(rpm)에 대한 토크(Torque)와 출력을 각각 그래프로 나타내었다. 표 2는 난류 모델에 따라 계산된 토크값을 보간법에 의해 스플라인 커브로 변환하여 최대값을 나타낸 결과이다. 본 연구에서 설계한 풍력터빈의 경우 난류 모델에 상관없이 300W의 발전 성능을 보여주고 있으며, 난류 모델에 따라 상이한 회전속도에서 계산된 토크와 출력의 최대값은 k - ϵ > k - ω > SST 순으로 확인된다.
풍력터빈 발전 성능 예측에 가장 중요한 변수로 앞서 계산된 해석 결과로부터 풍속(Vw)에 대한 블레이드 끝단부 속도(Vtip) 비율을 식 (3)과 같이 주속비(⋋)로 나타내며, 풍력에 의한 블레이드에서의 출력 P[W]는 공기 밀도(ρ)와 풍속(Vw)과의 관계는 식 (4)와 같이 산출할 수 있다[9].
| (3) |
| (4) |
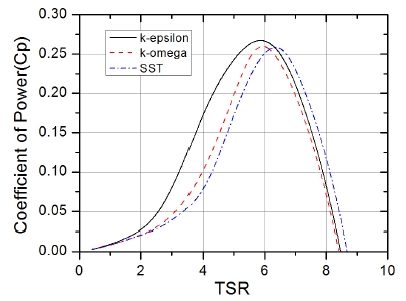
그림 9는 본 연구에서 설계한 풍력터빈의 주속비(⋋)에 대한 출력계수(Cp)에 대하여 그래프로 나타내었으며, 표 3은 조건별 주속비에 대한 출력계수의 최대값을 나타내었다. 계산 결과 k - ϵ은 주속비 5.860에서 0.267의 최대 출력계수값을 알 수 있으며, k - ω는 주속비 5.933에서 0.259, SST는 주속비 6.347에서 k - ω와 비슷한 0.258의 결과를 보이고 있다.
Ⅳ. 결론 및 향후 과제
본 연구는 300W급 다운윈드형 소형 수평축 풍력 터빈의 성능 검증을 하였다. NACA 4412, NACA 6415, NACA 6418을 혼합 설계한 블레이드를 활용하여 10㎧에서 300W급 발전이 가능한 풍력터빈을 설계하였다.
풍력터빈의 성능 예측을 위하여 유동해석을 진행하였으며, 가장 많이 사용되는 난류모델 k - ϵ, k - ω, SST를 사용하여 비교 검증하였다. 수치해석으로 풍속에 의해 발생되는 블레이드에서의 토크값을 계산하여 블레이드의 회전 속도와 곱하여 기계적인 출력을 계산하였다.
계산 결과 난류모델에 따른 회전속도와 토크, 출력에 대한 결과와 주속비와 출력계수에 대한 값을 확인하였다. 최대 토크와 출력, 출력계수는 k - ϵ > k - ω > SST 순이고, 각각의 난류 조건에서 토크, 출력, 출력계수는 회전속도가 k - ϵ < k - ω < SST 순으로 증가한다. 후류의 속도 분포가 클수록 토크가 큰 것을 확인하였다.
해석 결과를 기반으로 풍속 10㎧에서 3가지 난류 모델 모두 발전 성능이 300W가 가능하다고 확인하였다. 본 연구 결과를 기반으로 시제품을 제작하여 설계에 대한 시험 검증을 진행하고자 한다.
References
-
A. Messineo, and S. Culotto, "Evaluating the Performances of Small Wind Turbines: A Case Study in the South of Italy", Energy Procedia, 16, p137-145, Dec.), (2012.
[https://doi.org/10.1016/j.egypro.2012.01.024]

- A. Ernesto, Á. Cesar, and B. Francisco, "Advanced methodology for feasibility studies on building-mounted wind turbines installation in urban environment: Applying CFD analysis", Energy, 167, p181-188, Jan.), (2019.
- S. Keith, W. Thomas, B. Jonathan, and C. Michael, "Small wind turbines in turbulent (urban) environments: A consideration of normal and Weibull distributions for power prediction", Journal of Wind Engineering and Industrial Aerodynamics, 121, p70-81, Oct.), (2013.
- J. H. Kim, J. B. Kim, and Y. L. Oh, "Performance Prediction of Wind Power Turbine by CFD Analysis", Transactions of the KSME B, 37(4), p423-429, Apr.), (2013.
- D. H. Lee, and J. C. Park, "A Study of Wind Turbine by Using ANSYS Program", The Journal of Korea Infromation Electron Communication Technology, 11(5), p565-571, Oct.), (2018.
-
J. O. Mo, and Y. H. Lee, "Rotor Blade Design of a 1㎿ Class HAWT and Evaluation of Aerodynamic Performance Using CFD Method", Journal of fluid machinery and systems, 15(1), p21-26, Feb.), (2012.
[https://doi.org/10.5293/kfma..2012.15.1.021]

- Y. S. Choi, T. S. Kim, S. H. Park, H. G. Kim, M. S. Sim, and J. C. Lee, "A Study on Development of Blade for 10㎾ Downwind Turbine", Proceeding of the KSMPE Spring Conference 2013, p121-121, May), (2013.
-
F. R. Menter, "Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications", AIAA Journal, 32(8), p1598-1605, Aug.), (1994.
[https://doi.org/10.2514/3.12149]

- W. Tong, "Wind power generation and wind turbine design", WIT press, p90-98, Apr.), (2010.

1994년 2월 : 조선대학교 우주항공공학과(공학사)
1996년 2월 : 전남대학교 기계공학과(공학석사)
2017년 8월 : 전남대학교 기계공학과(박사수료)
관심분야 : 풍력터빈시스템, CFD

2000년 2월 : 조선대학교 항공우주공학과(공학석사)
2010년 2월 : 조선대학교 항공우주공학과(박사수료)
2010년 3월 ~ 현재 : 조선이공 대학교 자동화시스템과 교수
관심분야 : 신재생에너지, CFD