3 자유도 회전 관절체에 대한 회전각도 계산 및 삼차원 복원
초록
본 논문에서는 자동 초점 기능이 있는 움직이는 카메라로 촬영한 이미지를 사용하여 1개의 회전 관절을 가진 관절체를 3차원으로 복원하는 새로운 방법을 제시한다. 모든 입력 이미지 장면은 다른 각도의 형상을 가진 회전 관절체로 구성된다. 먼저 고정 된 환경 물체에 존재하는 특징점을 사용하여 카메라의 내부 및 외부 매개변수를 최적화 기법을 사용하여 계산한다. 이후 고정된 부위와 회전하는 관절체의 부위에 대해 삼차원 복원작업을 수행한다. 회전 관절체 부위의 특징점들을 사용하여 각 입력 장면에 대해 관절체의 회전각도와 회전중심을 계산한다. 계산된 회전각과 회전 중심을 사용하여 회전 관절체에 대한 3차원 체적을 복원한다. 삼차원 관절체 복원을 위한 기본 개념은 각각의 관절에 대하여 별도의 삼차원 복원을 실시하고, 또한 각각의 관절과 카메라 사이에 촬영으로 인해 불변의 관계가 형성된다는 점이다. 하나의 회전형 관절체에 대한 회전각도 계산결과는 정답 각도와 비교되었고 각도 계산 오차가 작아서 삼차원 복원이 가능하다 .
Abstract
In this paper, we propose a new method to reconstruct three-dimensional articulated body with one revolute joint using images taken with a moving camera with autofocus function. All input image scenes consist of rotating joints with different angular shapes. First, an internal and external parameters of a camera are calculated using the reconstruct technique using the feature points on a fixed environmental object. Thereafter, a three-dimensional restoration operation is performed on the fixed part as well as on the rotating joint part. Using the feature points of the joint, we calculate the angle of rotation and center of rotation of a joint for each input scene. Using the calculated rotation angle and center of rotation, we reconstruct the three-dimensional volume of the rotating joint. The basic concept for reconstructing three-dimensional joints is that a separate three-dimensional reconstruction is performed for each joint, and an fixed relationship is established between each joint and the camera. The rotational angle calculation results for a rotating joint were compared with the correct angle. The angular computation error was small so that 3D reconstruction was possible.
Keywords:
camera calibration, three-dimensional volume reconstruction, texture mapping, kinematic structure of an articulated bodyⅠ. 서 론
현재 촬영에 사용된 하나의 카메라가 움직이면서 동시에 추적 대상의 물체가 움직일 때, 텍스쳐까지 포함한 삼차원 복원을 할 수 있는 방법은 없다. 본 논문에서는 추적된 관절체의 몸을 스캔한 삼차원 모델을 얻으려고 한다. 관절체 스캔의 필요성을 설명하기 위하여 물체의 예를 들면 군사 행진에 나타나는 미사일 발사체가 될 수 있다. 이러한 무기는 발사 전에 발사대를 세우게 된다. 이러한 행위는 적대국의 감시의 대상이 된다. 관절체 복원 작업이 성공하면 미사일 발사체가 각도를 세운 상황에 대한 촬영 정보가 없어도, 발사체가 발사대를 세웠을 경우 어떠한 실루엣이 될는지 알 수 있다. 이러한 실루엣이 감시 영상 중에 파악되면 적대국에서는 경계태세에 돌입하면 된다.
물체의 삼차원 복원은 동일비율[1]-[3] 또는 실제 크기[4]로 가능하다. 이미지를 사용하여 삼차원 물체를 스캔하려면 반드시 물체에 대한 다중 관점이 필요하다. 본 논문에서는 자동 초점 기능이 있는 움직이는 카메라를 이용하여 관절체를 촬영하며, 촬영된 이미지에서 관절 각도를 계산하여 계산된 각도와 3차원 복원 기법을 사용하여 관절체를 복원하는 방법에 관한 논문이다. 관절체 구조와 특징점 입력이 제공될 때, 본 논문에서 제시한 새로운 방법은 (1) 움직이는 카메라에서 촬영된 두 장의 입력 이미지를 비교하여 관절의 각도를 계산하는 방법 (2) 이미지에서 회전된 관절의 회전을 보정하되, 촬영에 사용된 카메라를 회전시켜 관절의 회전이 없는 것과 같이 카메라를 회전 시키는 방법이다. 계산된 결과를 사용하여 회전하는 관절을 가진 물체에 대하여 텍스쳐를 포함한 삼차원 복원을 한 것이다.
모든 3차원 복원 방법[1]-[5]을 이 목적으로 사용할 수 있다. 본 논문의 방법은 계산된 관절 각도를 이용하여 삼차원 복원에 응용한 것이다. 관절 형 신체의 정확한 삼차원 복원을 위해서는 고정된 물체를 이용하여 먼저 카메라 매개 변수를 계산해야 한다. 계산 된 카메라 매개 변수를 기반으로 회전 부위의 삼차원 회전각도 및 회전중심을 계산한다. 회전각도는 회전체의 삼차원 복원을 위해 계산된 카메라 위치 및 방향을 보정하는데 사용된다.
이미지의 특징점을 사용하여 삼차원 복원을 하기 위하여 많이 쓰이는 방법은 2가지가 있다. 한가지 방법[1]-[3]은 특징점들의 연관관계를 이용하여 F행렬을 구해내고 F행렬을 분해하여 투사형 카메라의 위치 및 방향을 알아낸다. 이후 원래 삼차원 공간과 동일한 비율의 카메라의 위치 및 방향을 방정식을 풀어서 알아낸다. 다른 방법[4]은 격자 무늬를 사용하는 것인데 이 방법은 실제 크기를 알려준 것과 동일한 효과를 가진다. 격자무늬에서 카메라의 위치 및 방향을 계산해 내는 방식이다. 어떠한 방식을 사용하든지 정확한 카메라 내부 파라미터와 위치 방향을 계산하기 위하여 계산의 마지막 단계에서 최적화 작업을 거쳐야 한다.
본 논문에서 사용한 카메라 교정 및 삼차원 장면 분석을 위한 방법[5]은 Zhang의 방법[4]에서 파생된 것이다. 그러나 이 논문의 주요 기여는 카메라가 움직이고 촬영된 부분에서 회전하는 관절이 포함된 장면에서 관절의 각도 계산 방법이다. 또한 이 정보를 이용하여 텍스쳐를 가진 관절체를 삼차원 복원하였다. 삼차원 장면 분석을 위한 우리의 방법은 변수로 카메라 매개 변수뿐만 아니라 삼차원 물체상의 특징점에 대한 위치 오차가 최소가 되도록 최적화한다. Zhang의 교정 방법에서는 사람이 만든 격자 패턴 이미지가 일반적으로 카메라 교정에 사용된다. 실생활에서 포착하는 장면에서 때로는 직각에 가까운 모양이나 알려진 면이 있는 격자 무늬를 발견 할 수 있다. 이 패턴은 세계 좌표에서 대상 객체의 점에 대한 단서를 제공한다. 우리의 방법을 사용하여 실제 좌표 점이나 크기를 알고 있다면 복원 된 물체의 실제 크기를 계산할 수 있다.
관절체에 대한 삼차원 복원을 위해서는 관절의 각도 계산이 필요하다. 현재까지 관절체의 표면까지 복원한 논문은 없다. 다만 관절체의 궤적을 계산하기 위한 논문은 특징점의 움직임을 행렬로 표현하고 특이값 분해 기법[6]-[8]을 사용하여 관절의 위치를 찾아내나, 관절체 표면에 대한 복원은 여태까지 되지 않았다. 본 연구에서는 최적화 기법을 사용하여 정확한 관절의 위치 및 각도를 계산하여 관절체 표면에 대한 복원까지 수행한다.
Ⅱ. 관련 연구
삼차원 복원을 위해서, 이 논문에서 사용하는 방법은 다중 관점의 수동적 방식으로 분류된다. Hartley의 책[1] 및 Moons 논문[3]와 같은 이전 연구는 삼차원 복원을 위한 유용한 참고 자료이다
많은 방법들[9]은 특징점을 기반으로 한다. 많은 알고리즘은 삼차원 복원을 위한 초기화가 필요하다. 또한 여러 방법[10]들은 전경 및 배경 분할이 필요하다. 삼차원 복원을 위해 shape-from-silhouette [11][12]를 사용했다. 이 방법은 물체를 여러 관점에서 찍은 실루엣 이미지를 사용하는데, 2차원 실루엣의 각 픽셀은 관찰용 피라미드가 되고 삼차원 물체를 재구성하기 위하여 다시 거꾸로 투영된다. 여러 장면에서 실루엣 부분만 남기고 제거한 결과 삼차원 체적을 생성할 수 있다. 거꾸로 투영하여 만든 삼차원 물체의 표면 복셀에 대하여 어떤 장면의 어떤 픽셀에서 투사가 가능한지 확인한다. 각 장면 픽셀의 평균을 그 복셀에 대한 색으로 결정하면 텍스쳐를 가진 삼차원 물체를 복원할 수 있다. 본 논문에서는 공간 조각 알고리즘[13]을 사용했다.
각각의 관절에 대해서도 위와 동일한 방법으로 복원이 가능하다. 다만 관절은 움직이므로 관절의 움직임을 먼저 계산해야한다. 관절을 찾아내는 핵심 아이디어는 각 관절 몸 부위의 교차 공간을 계산하는 것이다[6]-[8]. 관절체가 동작하는 공간끼리 교차점이 있으면 관절체 토막을 연결하는 링크가 있는 것을 이용한다. 이를 위하여 특징점의 움직임을 행렬로 표현하고 행렬에 대해 특이값 분해 기법을 사용한다. 결과 존재하는 영(Null) 공간 관련식을 풀어서 관절의 위치 및 구조를 찾아낸다. 이상의 방법은 관절체에 대한 대략의 복원만 가능하다.
Ⅲ. 제시된 방법의 개요
우리의 접근 방식은 기존의 연구 결과[6]-[8] 혹은 사용자의 입력으로 관절 구조에 대한 정보를 미리 입력으로 받아서 정확한 관절 각도와 관절 위치 계산을 통하여 관절체에 대한 삼차원 복원을 시도하므로 기존의 방법들에서 시도하지 못한 관절 표면을 포함한 관절체 복원이 가능하다. 다만 본 논문에서 제시한 방법의 약점은 필요한 추가의 정보를 사용자 혹은 다른 알고리즘에서 관절구조 및 특징점 정보를 받아서 활용했다는 점이다.
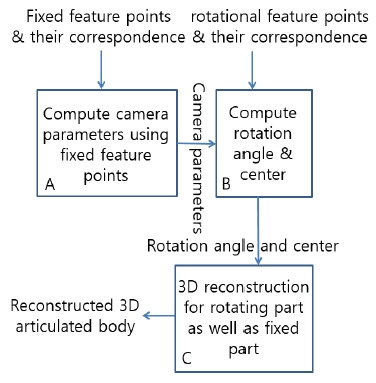
그림 1은 촬영된 이미지에서 관절체의 정확한 회전 각도를 계산한 후, 입력 이미지에서 회전된 관절의 회전을 보정하되, 촬영에 사용된 카메라를 회전시켜 애초 관절의 회전이 없는 것과 같이 카메라를 회전 시킨 후, 관절 회전이 없었던 상황의 삼차원 물체에 대한 텍스쳐 매핑 된 삼차원 복원의 계산 흐름을 보여준다. 본 논문에서는 관절의 회전 각도를 계산하는 방법과 카메라를 관절의 회전에 따라 회전을 시키는 방법에 중점을 둔다.
모든 입력 이미지는 회전각도가 다른 관절을 포함된다. 계산 단계 (A)는 삼차원 장면의 특징점 좌표 계산 및 카메라 파라미터 계산이다. 본 논문에서는 장면의 이미지를 찍기 위해 다양한 초점 거리의 움직이는 카메라를 사용하였고, 이 카메라의 외부 파라미터뿐만 아니라 내부 파라미터도 계산한다.
계산 단계 (B)는 입력 장면끼리 비교하여 회전 관절 부위의 회전각도와 회전 중심을 생성한다. 이를 위하여 이미 제공된 관절 구조에 기초하여, 움직이는 특징점 및 그들의 대응 관계의 입력을 사용한다.
계산 단계 (B)의 출력은 계산 단계 (C)에 공급되며, 여기에서 본 논문에서는 관절체의 회전 부위뿐만 아니라 고정된 부분에 대해서도 삼차원 볼륨을 계산한다. 계산 단계 (A)와 계산 단계 (B)에서 파라미터 최적화 방법을 사용하였다.
본 논문에서 사용 된 가정은 다음과 같다 :
- (1) 이미지 왜곡등 외부 내부 변수를 모르는 움직이는 카메라가 하나만 사용된다. 즉 초점 거리를 제외하고 촬영된 모든 이미지의 내부 변수는 동일하다.
- (2) 초점 길이가 변하며, 카메라의 위치 및 방향도 변화한다.
- (3) 추적 된 객체는 움직이는 카메라에 의해 추적되는 동안 고체물체인 것으로 간주된다.
- (4) 모든 입력 이미지는 회전각이 다른 회전 부위를 포함하는 삼차원 회전 관절을 가진 몸체를 갖는다.
- (5) 다른 알고리즘[6]-[8] 또는 사용자 입력을 이용하여 특징점 계산과 특징점 간의 대응 관계가 제공된다.
- (6) 회전하는 몸체뿐만 아니라 정지 된 배경 물체에서도 특징점을 발견 할 수 있다.
- (7) 전경 및 배경 부분들에 대한 정보가 존재한다.
- (8) 관절 구조에 대한 정보가 존재한다.
Ⅳ. 카메라 보정 계산 및 3D 장면 분석
4.1 확장 쿼터니언[14]
확장된 쿼터니언(Quaternion)의 개념은 최적화 기법을 사용하는데 있어서 변수의 수를 줄이기 위해 사용되었다. 쿼터니언은 회전만 가능하고, 이를 보완하기 위하여 이동기능이 포함된 확장 쿼터니언을 사용하였다. 이해를 돕기 위하여 본 논문의 방정식은 행렬 기반으로 제시되었으나, 실제 구현은 쿼터니언으로 되어 있다.
4.2 좌표계 변환에 사용되는 표기법
두개의 삼차원 좌표계 간의 좌표계 변환을 나타 내기 위해,본 논문에서는 일반적으로 4 × 4 호모지니어스(Homegeneous) 변환 행렬을 사용한다. 표기법 은 B 좌표계 관점으로 표현된 정보를 A좌표계 관점으로 변환하기 위해 사용한다. 본 논문에서 표현된 모든 변환행렬은 확장 쿼터니언을 사용하여 실제 코딩되었다.삼차원 기준 좌표계는 W로 표시하는 반면, 이차원 이미지 좌표는 I로 표시하기로 한다.
4.3 고정 장면 분석 및 카메라 보정 계산
우리의 3D 복원 방법은 Zhang의 방법[4]의 변형이다. 3D 장면 분석 및 카메라 보정 방법은 본 논문의 핵심이 아니다. 카메라 보정을 위한 파라미터 최적화 기법은 Zhang의 방법과 비슷하다. 이 부분은 어떠한 3D 복원 알고리즘[1]-[4]으로도 바꿀 수 있다.
만일 추적 대상 물체에 삼차원 특징점들이 있고 이들 중 k번째 특징점을 Mk라 두자. 이 점들은 매 장면 이미지에 투영된다. 물론 이 점의 위치는 매 장면 변화하며 그 위치는 당장 알 수 없다. 만일 촬영된 두 장면 i와 j가 있다고 가정하고, 이 특징점을 가진 관절체 부위가 움직이지 않았다고 가정하자. Mk점이 이미지 i에 투영될 때는 투영된 점이 mik이고, 이미지 j에 투영될 때는 투영된 점이 mjk라 가정한다. 이미지 i와 이미지 j를 사용하여, 카메라에서 해당 이미지 픽셀로 광선총이 발사되었다고 가정한다.
관절체가 움직이지 않았으므로 각 이미지에서 발사한 광선총은 삼차원 특징점 Mk에서 만나야 한다. 이미지 i에서 발사된 광선식을 라고 하고, 이미지 j에서 발사된 광선식을 라 한다. 두개의 광선이 교차하면 삼차원 점은 Mk로 계산된다. 카메라 왜곡 등으로 광선이 만나지 않으면 두 광선사이 최단 거리를 만드는 선의 중간 점을 교점 로 간주한다. 계산된 교점 을 다시 이미지에 거꾸로 투영해 본다. 이미지 i에 투영될 때는 mik이고, 이미지 j에 투영될 때는 mjk 여야 하는데, 계산된 Mk를 투영한 것과 실제 이미지 특징점 사이 괴리를 계산하여 괴리가 줄어들도록 카메라 내부 및 외부 파라미터 등 변수를 수정하여 오차를 최소로 하는 장면값을 최적화 과정을 거쳐 알아내게 된다.
여기서 A는 카메라의 내부 파라미터를 나타내는 고유 행렬이고, Ri는 i번째 이미지를 촬영한 카메라의 회전 행렬이며, 는 i번째 이미지를 촬영한 카메라의 위치 벡터이고, 는 A, Ri, 의 파라미터를 가진 카메라를 이용하여 이미지 i에서 Mk인 삼차원 점을 필름에 투영시킨 결과 픽셀점이다.
이러한 계산 결과에서 본 논문에서는 카메라의 내부 및 외부 파라미터를 얻는다. 파라미터 값은 (B)단계 및 (C)단계에서 사용된다. 이 과정은 다른 방법들을 이용하여 계산할 수 있는 부분이다.
Ⅴ. 관절 각도 및 길이 계산
본 절은 논문[15]에 비해 수식이 구체화된 버전이다. 본 논문에서는 사용자가 사전에 관절각을 계산할 관절체의 구조를 알고 있다고 가정했다. 이 관절 구조는 길이는 미지수 이지만, 모든 관절은 3차원 회전을 하는 것으로 설정된다. 복잡한 체인 형태로 엮인 트리 구조의 관절체에 대한 관절각도 계산은 차후의 연구에서 수행하며, 본 연구에서는 1단계의 삼차원 회전 관절 구조를 가진 구조체의 관절 각도를 계산한 후, 관절 각도의 정확도를 검증하기 위하여 삼차원 복원을 실시하기로 한다.
여러 장면의 회전 각도를 계산하기 위해 하나의 장면/프레임을 기준 프레임으로 설정하고, 이 장면에 비하여 관절의 회전 각도를 나타낸다. 삼차원 복원을 수행할 때에도 이 장면의 형상을 기준으로 관절체의 삼차원 복원이 일어나게 되는 것이다.
이 장면을 촬영하기 위한 카메라의 내부 외부 파라미터는 계산 단계 (A)에서 고정된 배경 장면을 이용하여 알아내었다. 이미지 i와 이미지 j에 각각의 이미지에 나타나는 동일한 특징 점 Mk이 있다고 가정한다. 또한 각 장면에서 나타나는 특징점 간의 대응 관계 정보가 제공된다고 가정한다. 각 카메라에 투영된 하나의 특징점에 해당하는 하나의 광선 벡터가 발사되는 것으로 가정할 수 있다. 카메라 i의 좌표계를 Ci라 하자. 이 카메라 좌표계의 Z축에 수직으로 설정된 이차원 이미지의 k번째 특징 벡터는 이차원으로 볼 때 mik이미지 픽셀로 나타나고, 이 픽셀을 이용하여 Ci의 원점에서 발사하는 광선 벡터를 가정할 수 있다. 마찬가지로 카메라 j의 좌표계를 Cj라 하자. 이 카메라 좌표계의 Z축에 수직으로 설정된 이차원 이미지의 k번째 특징 벡터는 이차원으로 볼 때 mjk 이미지 픽셀로 나타나고, 이 픽셀을 이용하여 Cj의 원점에서 발사하는 광선 벡터를 가정할 수 있다. 초점 거리 fi는 이미지 i의 촬영에 사용되며 초점 거리 fj는 이미지 j에 사용된다. 의 변환 행렬은 W 또는 기준 좌표계에서 관찰한 Ci 좌표계를 뜻한다. Mk는 기준 좌표계의 고정된 물체에 있는 k번째 삼차원 점이라고 가정하고 이 특징점은 촬영에 사용된 각 이미지에 투영된다. 이 점은 각각 mik 및 mjk로 표시된 이미지 i 및 이미지 j의 픽셀로 관측 될 수 있으며, Mk의 삼차원 위치는 알려져 있지 않다.
Ci의 원점에서 Mk로 발사하는 광선 벡터를 라 하고, Cj의 원점에서 Mk로 발사하는 광선 벡터를 라고 하자. ⊕는 광선 교차 테스트를 나타낸다. 두개의 광선이 교차하면 교차점은 로 계산된다. 정확히 만나지 않는 경우, 두 광선 간의 최단 거리를 만드는 선의 중간점을 교차점으로 간주한다. 는 다시 Ci와 Cj측으로 투영된다. 투영된 픽셀과 실제 입력 위치 mik 및 mjk와의 불일치를 최소화하는 최상의 카메라 내부 및 외부 매개 변수, 관절 회전 중심 및 관절 회전각도 값 등을 찾는다.
고정된 장면의 경우와 마찬가지로 관절각도 계산은 일종의 광선 교차 테스트를 통하여 각도가 결정된다. 여러 장의 입력 이미지에서 모든 장면의 관절의 각도는 다른 것으로 가정한다. 우리가 추적 대상으로 하는 물체는 관절을 가지고 있다. 관절체의 일부가 회전한다. 회전각도 및 회전 중심을 정확히 보정해 줘야 한다. 회전하는 대상에서 k번째 삼차원 점을 계산하려면 임의의 점 중심 삼차원 회전 계산을 포함해야한다. 다행히 입력 장면에는 움직이지 않는 환경 물체들이 있다. 이 물체의 특징점을 이용하여 카메라의 위치 및 방향, 초점 거리, 왜곡등 정보를 알아낼 수 있다.
회전 중심까지의 벡터 는 기준 좌표계 W의 관점에서 미지의 위치 벡터인데, 관절의 회전 중심을 나타낸다. t와 s는 광선의 파라미터를 사용한 표현에 사용되는 매개 변수이다. t와 s는 카메라 중심에서 교점까지 거리 정보를 나타낸다. 관절각도 계산은 임의의 축 중심 회전으로 우리가 평상시 사용하는 카테시안 좌표 공간과 다르므로 투영된 픽셀의 차이만으로 관절 각도를 정확히 계산하기에는 한계가 있다. 관절각도 계산에 카메라 중심에서 교점까지 거리 정보를 사용하면 회전에 관련된 문제를 카테시안 공간의 문제로 바꾼 효과를 가지게 된다. 이미지 i와 이미지 j에 나타나는 관절체 상의 특징점인 Mk는 두 이미지에서 공통적으로 관찰되는 점이라고 가정한다. 이미지 j에 나타나는 관절체는 관절체의 이미지 i에 나타나는 관절체에 비해 미지의 각도로 회전하였다고 가정한다. 는 이미지 i에 나타난 관절체가 회전을 하여 나타내는 이미지 j에 나타나는 관절체가 되었을 경우, 관절의 삼차원 회전에 관련된 4 × 4 행렬이다.
관절체 회전부위의 k번째 특징 점은 회전 중심을 사용하여 에 의해 회전된다. 이미지 i와 이미지 j로부터 삼차원 특징점 Mk에 대해 두개의 광선이 발사된다고 가정 할 수 있다. 그러나 관절체는 이미지 j 장면에 비해 회전한 상태이므로 이에 대한 보정을 해 주어야 한다. 회전 중심 와 회전각 를 미지수로 하는 최적화 문제를 풀면 된다.
이미지 i측의 광선은 회전을 한 후 이미지 j측의 광선과 교차점을 비교한다. 는 의 회전 중심을 사용하여 만큼 회전된다. 본 논문에서는 을 회전시킨 광선식과 두 광선 사이의 교차 시험을 수행한다. 는 4 × 4 이동을 위한 호모지니어스(homogeneous) 좌표계 이다. 이 계산 단계 (B)를 위한 광선 교차 테스트 ⊕는 다음의 식 (1)을 이용하여 수행할 수 있다.
| (1) |
식 (2)는 최적화 방법을 사용하여 관절각 및 회전 중심을 계산하기 위한 식이다. 와 사이의 가장 짧은 거리를 만드는 라인의 중간 지점을 라고 하자. 그러면 이미지 j에 이 투영되고 2D에서 k번째 입력 특징 점인 mjk와 계산 후 투영된 점 과 오차를 평가한다. 오차를 최소화시키는 관절의 회전 중심과 회전 각도를 찾는 작업을 수행하고, 최적 값에 도달했다고 판단되면 이 최적화 작업을 종료한다. 여기서 최적의 값을 저장하는 변수들은 와 인데 i와 j의 범위는 1에서 n까지 이며, 다만 i≠j이며, n은 관절체 삼차원 복원에 사용된 입력 이미지의 숫자이다. 총 n개의 입력 이미지가 있으므로, 하나의 특징점에 대하여 n-1번 비교가 발생한다. 최적화 목적함수는 다음과 같다.
| (2) |
여기서 A는 카메라 내부 파라미터 등을 포함한 고유의 행렬이고, 는 i번째 촬영한 카메라의 방향 행렬이며, 는 기준 좌표계 관점에서 i번째 카메라의 이동 벡터이고 는 계산된 교점인 삼차원 점 을 j번째 촬영한 카메라의 이미지 j에 투영할 때 맺히는 픽셀이다. w1는 계산된 값과 입력 특징점간의 특징점 이격도를 줄이기 위한 가중치이고 w2는 안정된 교차점을 계산하기 위하여 카메라와 계산된 삼차원 특징점 사이 거리가 일정해야 함에 대한 가중치이다.
본 논문에서는 에 대해 세 개의 변수를 사용했고, 를 표현하기 위하여 쿼터니언을 사용하였으며 이를 위해 네 개의 변수를 사용했다. 다만 쿼터니언 하나당 제약식 하나가 발생한다. n 입력 이미지의 경우 계산단계 (B)를 위해 (4(n-1) +3)개의 변수와 (n-1) 쿼터니언 제약 방정식을 사용했다. 단계(B)의 계산 결과로 i번째 이미지를 기준 이미지로 설정하여 각 입력 이미지에서 회전 관절체의 회전각도 및 회전 중심을 얻는다. 결과는 그림 계산 단계 (C)에서 사용된다.
Ⅵ. 관절체의 삼차원 복원
6.1 고정된 관절체의 삼차원 복원
이 절은 Moons 논문의 섹션 1.4.5와 매우 유사하다[2]. 이 과정을 ''실루엣에서 모양추출(Shape–from-silhouette)''이라고 한다. 삼차원 관절 복원 작업으로 각 관절별로 배경이 제거된 입력 이미지가 주어지고, 또한 특징점들 좌표 및 대응 정보도 제공된다. 사용자가 체적의 세밀도 혹은 복셀의 크기를 입력한다.
삼차원 관절체 복원 알고리즘을 이해하는 데 도움이 되도록 실제 입력 이미지를 사용하여 알고리즘을 설명한다. 실험에 사용된 모든 복원 작업에서 총 4개의 입력 이미지가 사용되었다.
6.2 회전하는 관절체 부위의 삼차원 복원
관절체의 삼차원 복원을 위한 기본 개념은 각 관절 부위 각각을 복구하는 것이다. 그림 2(a)는 회전하는 관절을 포함한 입력 이미지를 보여준다. 여자의 머리는 모든 입력 이미지에서 다른 이미지에 비해 회전되었다. 그림 3(a)는 관절체의 입력 이미지를 보여준다. 마네킹의 왼쪽 팔은 모든 입력 이미지에 대해 회전하고 있다. 카메라 내부 파라미터 계산이 끝나면, 다음 계산 단계에서 회전 중심 및 회전 각도를 계산해야한다. 몸체의 회전 부분의 삼차원 관절체 복원을 위해, 각 관절 부분이 각각의 삼차원 복원이라고 가정 할 수 있다. 모든 복원은 관절별로 따로 일어난다.
고정된 부위에 대한 복원은 어떠한 알고리즘을 사용하여도 무방하다. 회전 부분의 삼차원 관절체 복원에 대해서는 관절의 회전 중심 및 회전각을 계산하여 애초에 촬영한 카메라에 대해서 위치 및 방향을 보정해 줘야한다. 회전 각도를 계산하기 위해 기준 장면 설정이 필수이다. 예로 프레임 번호 를 기준 장면으로 지정한 후, i를 기준으로 하여 회전각도 및 회전 중심을 계산한 후 삼차원 관절체 복원을 수행한다. 관절에 대하여 카메라로 촬영하는 순간, 관절과 카메라의 관계는 고정된 것이다.
기준 장면 i에 비하여 장면 j의 카메라가 관절에 따라 회전한 것으로 간주할 수 있으므로, 카메라도 같이 역으로 회전시켜 기준 장면 i에 맞추어 줘야 기준 장면에 해당하는 카메라 위치 방향을 알아낼 수 있다. 모든 삼차원 복원은 기준좌표계 W 기준으로 일어난다. 기준 장면을 고려하여 카메라 j의 위치와 방향을 보정하는 계산은 다음과 같다.
| (3) |
는 기준좌표계 W에서 Cj 좌표계를 관찰한 변환 행렬이고, 는 관절 회전이 보정된 카메라를 관절 따라 역회전한 새로운 카메라 변형 행렬로 변경된 값이다. 는 W의 관점에서의 회전 중심 벡터이다. 는 4×4의 호모지니어스 변환 행렬로 이미지 j에 나타난 관절의 회전을 역으로 회전하여 이미지 i에 비해 회전이 없는 것으로 변환하기 위한 회전 행렬이다.
그림 2(a)와 그림 3(a)의 왼쪽 제일 위 이미지가 삼차원 관절체 복원의 기준 장면으로 설정되었다. 그림 2(c)와 그림 3(c)는 고정된 부위에 대한 배경을 제거한 입력 실루엣을 보여주고, 그림 2(d)와 그림 3(d)는 회전되는 부위에 대하여 배경 제거된 입력 실루엣을 보여준다.
삼차원 관절체 복원을 위해. 계산 단계 (B)를 이용하여 회전 부위에서 특징점을 사용하여 회전 중심 및 회전 각도를 계산했다. 또한 삼차원 회전부위 복원을 위하여 방정식 (3)을 사용하여 회전이 없는 것처럼 카메라 위치와 방향을 보정했다. 보정 된 카메라 외부 파라미터를 사용하여 텍스처를 가진 삼차원 관절체 복원을 수행했다. 그림 2(b)와 그림 3(b)는 텍스처를 가진 삼차원 복원된 관절 모델 몸체 부위를 보여준다.
Ⅶ. 실험 결과
본 논문에서 사용된 환경은 이미지 왜곡 등 외부 내부 변수를 모르는 움직이는 카메라가 하나만 사용된다. 모든 입력 이미지는 회전각이 다른 회전 부위를 포함하는 삼차원 회전 관절을 가진 몸체를 갖는다. 관절 구조, 전경 및 배경 부분들에 대한 정보가 존재한다. 본 논문에서 제시한 방법은 기존 관절체 구조를 알아내는 방법의 결과를 입력으로 받아 관절체 표면까지 삼차원 복원이 가능하도록 수식을 개발하였으며, 개발한 수식에 대한 검증이 복원 결과로 행하여 졌다.
그림 2(b)와 그림 3(b)에서 카메라 위치 방향 보정 및 정확한 관절길이 및 관절각도 계산을 증명하기 위해 실루엣으로부터 다양한 삼차원 관절체 복원을 생성했다. 관절체 복원은 관절각의 오차가 조금만 생겨도 복원이 거의 불가하므로 특히 마네킹 관절체의 몸체 부위의 복원이 제대로 이루어 졌음을 확인할 수 있다. 마네킹은 관절이 3자유도이나, 사람의 목의 경우 더 많은 자유도라 오차가 있음을 복원 결과에서 알 수 있다. 본 논문에서는 배경이 제거된 이미지와 특징점 및 특징점 대응 관계를 입력으로 제공했다. 배경 제거 및 특징점 추출 알고리즘은 이 연구의 중심이 아니다. 모든 삼차원 관절체 복원을 위해 더 많은 입력 이미지가 보다 정확한 삼차원 관절체 복원을 생성 할 수 있지만 본 연구의 실험에서는 편의상 항상 4개의 입력 이미지 만 사용했다.
그림 2(a)와 그림 3(a)는 고정 된 배경 물체를 스캔하는데 사용되는 실제 4개의 입력 이미지를 보여준다. 표 1은 텍스처가 있는 다양한 삼차원 관절체 복원을 위해 사용되는 입력 점의 갯수를 나타낸다. 표 1(a-d)는 각각의 입력 이미지에 대해 고정 부위 및 회전 부위 각 부위 별로 사용된 점의 갯수를 보여준다. 각 점들의 상응하는 대응 관계는 사용자가 제공한다. 고정 부위 혹은 배경 물체 상의 특징점에 대한 삼차원 위치 정보는 회전이나 이동이 없는 점들에 대해 어떤 방법의 삼차원 복원이라도 적용시켜 계산할 수 있다. 모든 입력이미지는 장면에 나타나는 방의 벽에 삼차원 복원의 기준 좌표계의 원점이 설정되었다.
본 논문에서 제시한 방법을 사용하면 회전 중심을 계산할 수 있기 때문에, 회전 부분을 구별하는 것이 어렵지 않다. 각 이미지에 계산된 삼차원 회전 중심을 투영하고, 회전하는 부분에 대한 실루엣을 자르기만 하면 된다. 특징점을 사용하여 회전 중심뿐만 아니라 회전각도도 계산했다. 계산된 회전각도 값은 관절체의 삼차원 복원에 사용된다. 복원된 관절체는 그림 2(b)와 그림 3(b)에 나와 있다. 관절각 계산을 위해 회전체 상에 충분한 입력 특징점이 필요하다. 표 1에서 보는 바와 같이, 그림 2(d)의 경우 최대 9개, 그림 3(d)의 경우 최대 15개의 특징점을 사용하였다. 복원된 결과 특징점을 많이 사용한 회전체 경우가 더 정교한 복원이 되었음을 관찰할 수 있다.
관절 각도와 회전 중심을 계산하는데 있어서 식 (2)에는 국부적인 최적값이 존재한다. 국부 최적화를 극복하려면, 관절의 회전 중심을 계산하기 위한 변수의 초기값으로 관절 회전중심 부근의 특징점을 사용한다. 초기값이 정답 부근이므로 정확한 관절각도 및 회전 중심을 제대로 찾을 수 있다.
그림 2에서 매 입력 장면에서 모델 여자에게 머리의 회전을 멈추라고 요구하였고, 정지된 상황에서 모델을 여러 방향으로 여러 장 찍었다. 매 장면에 대하여 삼차원 복원이 가능하며, 정답 회전각도 계산도 가능하다. 특정 회전각도의 정지된 장면에 대한 삼차원 복원을 사용하여 모델 머리의 특징점 들에 대하여 삼차원 위치를 계산했다. 삼차원 위치를 이용하면 회전각도에 대한 정확한 값을 계산할 수 있다. 보다 더 정확한 계산을 위해서는 보다 많은 특징점들이 필요하다. 결과 모델의 셔츠에 대한 텍스쳐도 더 선명해질 것이다. 여자 모델의 모자 끝은 잘렸다. 이유 중 하나는 회전각도에 대한 부정확 한 계산 일 수 있다.
표 2는 본 논문의 계산 방법과 삼차원 복원을 이용한 정확한 위치를 이용한 회전각 차이를 쿼터니언을 사용하여 비교하였다. 그림 4는 굴삭기에 대한 삼차원 복원의 예를 보여준다. 삼차원 복원 방법은 앞의 방법과 동일하다. 총 111개의 특징점이 복원에 사용되었다.

Joint angles in quaternion computed using our approach versus corresponding angles computed using 3D reconstruction given Fig. 2 as input
두개의 쿼터니언 값 사이의 내적은 두개의 쿼터니언 값 사이의 회전 각 차이와 관련이 있다. 두개의 쿼터니온 내적 결과 값 1.0은 회전에 차이가 없음을 의미한다.
모든 코드는 GRG2[16]를 제외한 다른 라이브러리를 사용하지 않고 C 프로그래밍 언어로 작성되었으며, 본 논문에서는 하나의 IXY810 휴대용 디지털 카메라를 사용하여 이미지를 만들었다.
Ⅷ. 결 론
본 논문은 하나의 삼차원 관절을 가진 물체에 대한 삼차원 관절체 복원을 보여주었다. 관절체 삼차원 복원의 핵심은 관절 회전각도의 정확한 계산에 있다. 방정식 (3)의 회전 각 계산시 카메라와 특징점 간의 거리 정보인 t 및 s값에 불이익을 주었다. 이 작업으로 회전 좌표 값에서 직교 좌표 값으로 변환 할 때 발생하는 오류가 최소화되었다. 여러 입력 장면 중, 시간 변화가 작은 연속된 장면인 경우, 관절의 회전각이 작을 것이다. 회전각이 작은 입력 이미지는 매개 변수 최적화를 사용하여 회전 각도를 계산하는 것이 훨씬 더 쉽고 빠르다. 왜냐하면 정답 관절 값과 초기 관절 값이 비슷하기 때문이다. 많은 다른 연구와 유사하게, 본 방법의 단점은 특징점의 잘못된 입력으로 인해 발생하는 오차는 정확한 관절 각 계산을 방해한다.
우리의 계산은 파라미터 최적화에 의존하기 때문에 최적화에 사용되는 변수의 수를 압축하는 것은 매우 중요하다. 변수의 수가 증가하면 계산의 복잡성 및 계산 시간이 크게 증가하기 때문이다. 최적화에 사용 된 변수의 수를 줄이기 위해 본 논문에서는 이동 기능을 포함한 확장 쿼터니언을 사용했다. 우리의 계산 결과에 따르면, 그림 2의 여자 머리의 회전 중심이 그 여자의 입 뒤에 존재하는 것을 발견하였다. 인간의 머리의 자유도는 비록 3 자유도를 부여했지만 3 자유도가 아니다. 모델링 세부 사항을 높이려면 자유도를 늘려야한다. 그러나 자유도를 높이면 파라미터 최적화를 수행하기 위한 난이도가 증가한다. 이 이유로 인하여 본 논문에서는 3 자유도를 사용하였다. 그림의 인체 마네킹은 관절의 실제 자유도가 적다. 그러므로 마네킹 팔의 관절체 삼차원 복원 결과는 표 2에서 수치적으로도 확인할 수 있으며 그림 3(b)와 같이 여자 모델에 대한 복원 그림 2(b) 보다 훨씬 더 좋다.
그림 3(a)의 마지막 입력 이미지는 인체 모형의 어깨가 윗 팔을 가리는 장면을 보여준다. 복원 대상 물체 자체의 일부가 자기 자신의 다른 부분을 가리는 문제는 관절체 삼차원 복원의 또 다른 문제이다. 윗 팔의 절단을 피하기 위해 왼쪽 팔 끝의 실루엣을 그림 3(d)와 같이 좀 더 확장하였다.
실험 결과는 관절체에 대한 텍스쳐를 포함한 삼차원 복원 알고리즘이 잘 작동함을 보여준다. 정확한 카메라 보정은 물론 자동 초점 기능이 있는 움직이는 단일 카메라에서 굴절된 몸체를 회전시킨다.
우리의 계산은 파라미터 최적화 과정과 삼차원 복원을 사용하기 때문에 계산은 실시간으로 수행 될 수 없다. 움직이지 않는 일반 물체에 대한 삼차원 복원은 여러 다양한 방법으로 대체 될 수 있다.
여태까지 텍스쳐를 포함하는 관절체에 대한 삼차원 복원은 존재하지 않는다. 본 논문을 통하여 정확한 텍스처를 가진 관절체에 대한 삼차원 복원을 위한 가능성을 제공함으로써, 본 논문에서는 관절의 나무 구조로 구성된 복잡한 관절체에 대한 삼차원 복원법에 대한 방향을 제시한다.
Acknowledgments
이 논문은 2017학년도 홍익대학교 학술연구진흥비에 의하여 지원되었음
References
- R. Hartley, and A. Zisserman, "Multiple View Geometry in Computer Vision", 2ed., Cambridge University Press, (2004).
- M. Pollefeys, R. Koch, and L. V. Gool, "Selfcalibration and metric reconstruction in spite of varying and unknown intrinsic camera parameters", International Journal of Computer Vision, 32(1), p7-25, Aug.), (1999.
-
T. Moons, L. van Gool, and M. Vergauwen, "3d reconstruction from multiple images, part I: Principles", Foundation and Trends in Computer Graphics and Vision, 4(4), p287-404, Apr.), (2010.
[https://doi.org/10.1561/0600000007]

-
Z. Zhang, "A flexible new technique for camera calibration", IEEE Trans. Pattern Analysis and Machine Intelligence, 22(11), p1330-1334, Nov.), (2000.
[https://doi.org/10.1109/34.888718]

- J. Park, and S. Park, "Improvement on Zhang’s camera calibration", Applied Mechanics and Materials, 479-480, p170-173, Dec.), (2013.
- J. Yan, and M. Pollefeys, "A factorization-based approach to articulated motion reconstruction", IEEE Conference on Computer Vision and Pattern Recognition, Sandiego, California, 2, p815-821, Jul.), (2005.
-
J. Yan, and M. Pollefeys, "A general framework for motion segmentation: independent, articulated, rigid, non-rigid, degenerate and non-degenerate", 4th European Conference on Computer Vision, Cambridge, UK, p94-106, Jun.), (2006.
[https://doi.org/10.1007/11744085_8]

-
P. Tresadern, and I. Reid, "Articulated structure from motion by factorization", IEEE Conference on Compter Vision and Pattern Recognition, Sandiego, California, p1110-1115, Jun.), (2005.
[https://doi.org/10.1109/cvpr.2005.75]

-
D. G. Lowe, "Distinctive image features from scale-invariant key-ponts", International Journal of Computer Vision, 60(2), p91-110, Nov.), (2004.
[https://doi.org/10.1023/b:visi.0000029664.99615.94]

-
O. Faugeras, E. Bras-Mehlman, and J. D. Boissonnat, "Representing stereo data with the delaunay triangulation", Artificial Intelligence, 44(1), p41-87, Sep.), (1990.
[https://doi.org/10.1016/0004-3702(90)90098-k]

-
A. Laurentini, "The visual hull concept for silhouette-based image understanding", IEEE Transactionson PAMI, 16(2), p150-162, Jul.), (1994.
[https://doi.org/10.1109/34.273735]

-
A Laurentini, "The visual hull of curved object", 7th International Conference on Compter Vision, Kerkyra, Greece, 1, p356-361, Sep.), (1999.
[https://doi.org/10.1109/iccv.1999.791242]

- K. Kutulakos, and S. Seitz, "A theory of shape from space carving", International Journal of Computer Vision, 38(3), p199-218, Jul.), (2000.
- J. Park, and S. Kim, "Kinematics and constrained joint design using quaternion", CISST, June), (2002.
-
J. Park, "Multiple image based human joint angle computation", Applied Mechanics and Materials, 865, p547-553, Jun.), (2017.
[https://doi.org/10.4028/www.scientific.net/amm.865.547]

-
L. S. Lasdon, A. D. Warren, A. Jain, and M. Ratner, "Design and testing of a generalized reduced gradient code for nonlinear programming", ACM Trans. Math. Software, 4(1), p34-50, Mar.), (1978.
[https://doi.org/10.1145/355769.355773]


1983년 2월 : 서울대학교 기계설계학과(공학사)
1985년 2월 : 한국과학기술원 전산학과(이학석사)
1990년 5월 : University of Texas at Austin, Department of Computer Sciences(이학석사)
1994년 8월 : University of Texas at Austin, Department of Computer Sciences(이학박사)
1986년 3월 ~ 1993년 8월 : 부산외국어대학교 컴퓨터공학과 조교수
1994년 8월 ~ 현재 : 홍익대학교 컴퓨터공학과 교수
관심분야 : 이미지 처리, 컴퓨터 그래픽스