균일 회절 이론을 이용한 통합마스트의 회절 간섭 분석

Ⅰ. 서 론

현대의 전투함은 그 임무를 수행하기 위하여 다양한 전자전 기능이 필요하다. 이를 위하여 전투함의 마스트에는 레이더, 통신 장비, 적외선 센서와 같은 다양한 장비들이 설치된다. 그러나 마스트에 설치되는 안테나가 많아질수록 전투함의 RCS는 크게 증가한다. RCS의 증가는 전투함의 생존성과 전투능력에 악영향을 끼친다. 이러한 문제점을 극복하기 위해 등장한 것이 통합마스트 (integrated mast)이다. 통합마스트는 하나의 구조물에 전투함에 필요한 센서와 안테나를 밀집시키고 그 구조물의 형상을 RCS를 감소시키는 형태로 결정한 것이다[1][2].

통합마스트를 채용할 경우 전투함의 RCS가 크게 감소하기 때문에 전투함의 생존성과 전투능력이 크게 향상된다. 통합마스트를 설계할 때 RCS와 함께 고려해야 할 항목은 안테나들 사이의 전자파 간섭이다[3]. H. Shin 등은 PO와 PTD 기반의 해석 코드를 이용하여 회절을 고려한 통합 마스트의 RCS를 해석 하였다[2]. X. Cheng등은 레이돔이 포함되어 있는 통합마스트에 설치된 안테나 사이의 EMI/EMC를 0.8 ~ 1GHz 대역에서 계산하였다[3]. B. Turetken등은 모멘트법을 이용하여 통합마스트를 실장한 배의 EMI/EMC를 HF 대역에서 계산하였다[4]. 고주파의 회절을 해석하는 균일회절이론(UTD, Uniform Theory of Diffraction)은 선박에서의 전자파 환경을 분석하기 위해 많이 사용되는 방법이다[5][6].

본 논문에서는 UTD를 사용하여 통합마스트의 안테나 사이의 간섭을 해석하고 상용 전자파 수치해석 S/W인 FEKO의 결과와 비교하여 해석 결과의 정확성을 상호 검증하였다. UTD 코드를 자체 개발함으로써 FEKO를 사용하여 계산하기 어려운 마스트의 크기 변화에 따른 회절 영향을 분석 하였다.

Ⅱ. UTD를 이용한 통합 마스트의 회절 해석

2.1 UTD 계산을 위한 표적의 모델링

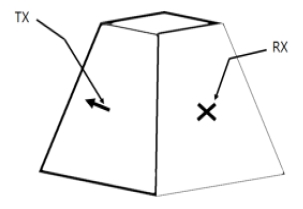
그림 1과 같은 형상의 통합 마스트를 가정한다. 통합 마스트의 한쪽 면에는 송신 안테나(TX)가 배치되어 있으며 다른 한쪽 면에는 수신 안테나(RX)가 배치되어 있다.

Fig. 1.

Integrated Mast including transmitting and receiving antenna

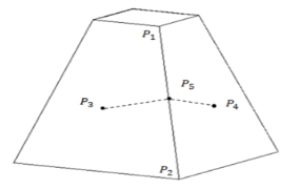
여기서 마스트의 모서리를 기준으로 보았을 때, 각 면에 설치된 TX와 RX의 위치 관계는 그림 2와 같다고 볼 수 있다.

Fig. 2.

Relationship between TX and RX antenna positions

2차원 모서리에 대한 회절파는 그림 2와 같이 3개의 영역으로 나눌 수 있으며 각 영역에 수신점이 위치할 경우 수신점에 도달하는 성분은 표 1과 같다[6]-[8].

Table 1.

Experimental data sets

본 논문에서 다루는 통합 마스트의 측면에 배치된 안테나들 사이의 커플링은 수신기의 위치가 항상 Region3에 위치한다. 따라서 회절파(Diffracted Field)의 영향만을 계산함으로써 수신점에 도달하는 전계를 계산할 수 있다.

UTD를 계산하기 위해서는 그림 1의 표적을 그림 3과 같이 3차원 직교 좌표계에 표현하여야 한다. 그림 3에서 P_k는 각각의 버텍스(Vertex)이며 식 (1)과 같이 3차원 벡터로 표현된다.

Fig. 3.

Integrated mast in 3-dimensional cartesian coordinate

$\[ P_k={\left[p_k^x{p}_k^y{p}_k^z\right]}^T \]$

(1)

여기서 P₁과 P₂는 엣지를 이루는 버텍스이며, P₃는 TX가 위치하는 마스트 표면의 위치벡터, P₄는 RX가 위치하는 마스트 표면의 위치벡터이다. P₅는 회절파가 지나가는 엣지상의 회절점이며 이는 Keller's laws of edge diffraction에 따라 식 (2)의 조건을 만족해야 한다[6-8].

$\[ \widehat{e}\bullet {\widehat{S}}_i=\widehat{e}\bullet {\widehat{S}}_r \]$

(2)

여기서 $$ \widehat{e}=\overrightarrow{P_1{P}_2}/‖\overrightarrow{P_1{P}_2}‖$$는 엣지의 단위방향벡터이며 $$ ‖\vec{X}‖={\left(\sum _{n=1}^N{\left|x_n\right|}^2\right)}^{1/2}$$이고, $$ \vec{X}={\left[x_1\cdots x_N\right]}^T$$이다. 식 (2)의 조건에 따라 P₅는 식 (3)과 같이 구할 수 있다.

$\[ P_5={\mathrm{m}\mathrm{i}\mathrm{n}}_{P_5}\left|\widehat{e}\bullet {\widehat{S}}_i=\widehat{e}\bullet {\widehat{S}}_r\right| \]$

(3)

여기서 $$ \overrightarrow{S_i}=\overrightarrow{{TP}_5}, \overrightarrow{S_r}=\overrightarrow{P_{5}R}$$이며 T는 송신기의 위치벡터 R은 수신기의 위치벡터이다. $$ \widehat{n_1}$$과 $$ \widehat{n_2}$$는 각 통합마스트 표면의 단위 법선벡터로서 식 (4), 식 (5)와 같이 정의된다.

$\[ \widehat{n_1}=\left(\overrightarrow{P_1{P}_3}\times \overrightarrow{P_1{P}_2}\right)/‖\overrightarrow{P_1{P}_3}\times \overrightarrow{P_1{P}_2}‖ \]$

(4)

$\[ \widehat{n_2}=\left(\overrightarrow{P_1{P}_2}\times \overrightarrow{P_1{P}_4}\right)/‖\overrightarrow{P_1{P}_2}\times \overrightarrow{P_1{P}_4}‖ \]$

(5)

2.3 수신점에 도달하는 전계의 계산

회절점 P₅로부터 수신점 R에 도달하는 전계를 계산하기 위해 UTD를 사용한다. UTD에서 회절점에 임의의 각도로 전계가 입사하였을 때, 회절에 의해 회절점에 도달하는 전계는 식 (11)과 같이 나타낼 수 있다[6]-[8].

$\[ \left[\begin{array}{c}{E}_{{\beta }_0}^d\hfill \\ E_{{\varphi }_0}^d\hfill \end{array}\right]=-\left[\begin{array}{cc}{D}_s\hfill & 0\hfill \\ 0\hfill & D_h\hfill \end{array}\right]\left[\begin{array}{c}{E}_{{{\beta }_0}^{\text{'}}}^i\hfill \\ E_{{{\varphi }_0}^{\text{'}}}^i\hfill \end{array}\right]{A\left(s^{\text{'}},s\right)e}^{-j\beta s} \]$

(11)

여기서 $$ E_{{\beta }_0}^d$$는 회절 전계 $$ \widehat{{\beta }_0}$$ 방향 성분이고 , $$ E_{{\varphi }_0}^d$$는 회절 전계의 $$ \widehat{{\varphi }_0}$$방향 성분이다. $$ s=‖\overrightarrow{S_r}‖$$은 회절점과 수신점 사이의 거리이며 $$ E_{{{\varphi }_0}^{\text{'}}}^i=\widehat{{{\varphi }_0}^{\text{'}}}\bullet \overrightarrow{E^i}$$는 회절점에 입사하는 전계의 $$ \widehat{{{\varphi }_0}^{\text{'}}}$$ 방향 성분이고 $$ E_{{{\beta }_0}^{\text{'}}}^i=\widehat{{{\beta }_0}^{\text{'}}}\bullet \overrightarrow{E^i}$$는 회절점에 입사하는 전계의 $$ \widehat{{{\beta }_0}^{\text{'}}}$$ 방향 성분이다. 방향 벡터 $$ \widehat{{\varphi }_0}=\widehat{e}\times \widehat{S_r}/‖\widehat{e}\times \widehat{S_r}‖, \widehat{{\beta }_0}=\widehat{{\varphi }_0}\times \widehat{S_r}/‖\widehat{{\varphi }_0}\times \widehat{S_r}‖, $$$$ \widehat{{{\varphi }_0}^{\text{'}}}=\widehat{e}\times \widehat{S_i}/‖\widehat{e}\times \widehat{S_i}‖, \widehat{{{\beta }_0}^{\text{'}}}=\widehat{{{\varphi }_0}^{\text{'}}}\times \widehat{S_i}/‖\widehat{{{\varphi }_0}^{\text{'}}}\times \widehat{S_i}‖$$과 같이 결정할 수 있다.

식 (11)에서 A(s^', s)는 공간 감쇄 팩터(Spatial Attenuation Factor) 이며, 이는 입사 전계가 어떤 형태를 갖는지에 따라 표 2와 같이 결정할 수 있다[6]-[8].

Table 2.

Types of spatial attenuation factor

본 논문에서는 spherical wave incidence를 가정하여 $$ A\left(s^{\text{'}},s\right)=\sqrt{\frac{s^{\text{'}}}{s\left(s^{\text{'}}+s\right)}}$$와 같이 결정 하였다.

식 (11)에서 D_s와 D_h는 회절 계수이다. UTD에서 D_s와 D_h는 식 (12)와 식 (13)과 같이 계산할 수 있다[6]-[8].

$\[ \begin{array}{c}{D}_s\left(L,\varphi ,{\varphi }^{\text{'}},n,{\beta }_0\right)=-\frac{e^{-j\frac{\pi }{4}}}{2n\sqrt{2\pi \beta } \mathit{sin}\left({{\beta }_0}^{\text{'}}\right)}\times \hfill \\ \left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi +\left(\varphi -{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{+}\left(\varphi -{\varphi }^{\text{'}}\right)\right)+\left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi +\left(\varphi -{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{-}\left(\varphi -{\varphi }^{\text{'}}\right)\right)\right\}\right\}\hfill \\ \begin{array}{c}+\frac{e^{-j\frac{\pi }{4}}}{2n\sqrt{2\pi \beta } \mathit{sin}\left({{\beta }_0}^{\text{'}}\right)}\times \hfill \\ \left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi +\left(\varphi +{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{+}\left(\varphi +{\varphi }^{\text{'}}\right)\right)+\left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi -\left(\varphi +{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{-}\left(\varphi +{\varphi }^{\text{'}}\right)\right)\right\}\right\}\hfill \end{array}\hfill \end{array} \]$

(12)

$\[ \begin{array}{c}{D}_h\left(L,\varphi ,{\varphi }^{\text{'}},n,{\beta }_0\right)=-\frac{e^{-j\frac{\pi }{4}}}{2n\sqrt{2\pi \beta } \mathit{sin}\left({{\beta }_0}^{\text{'}}\right)}\times \hfill \\ \left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi +\left(\varphi -{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{+}\left(\varphi -{\varphi }^{\text{'}}\right)\right)+\left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi +\left(\varphi -{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{-}\left(\varphi -{\varphi }^{\text{'}}\right)\right)\right\}\right\}\hfill \\ \begin{array}{c}-\frac{e^{-j\frac{\pi }{4}}}{2n\sqrt{2\pi \beta } \mathit{sin}\left({{\beta }_0}^{\text{'}}\right)}\times \hfill \\ \left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi +\left(\varphi +{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{+}\left(\varphi +{\varphi }^{\text{'}}\right)\right)+\left\{\mathrm{c}\mathrm{o}\mathrm{t}\left(\frac{\pi -\left(\varphi +{\varphi }^{\text{'}}\right)}{2n}\right)F\left({\beta Lg}^{-}\left(\varphi +{\varphi }^{\text{'}}\right)\right)\right\}\right\}\hfill \end{array}\hfill \end{array} \]$

(13)

여기서 L은 거리 변수이며, 입사 전계가 어떤 형태를 갖는지에 따라 표 3과 같이 결정할 수 있다[6]-[8]. 본 논문에서는 spherical wave incidence를 가정하여 $$ L=\frac{{ss}^{\text{'}} {\sin }^2{{\beta }_0}^{\text{'}}}{s+s^{\text{'}}}$$와 같이 결정 하였다

Table 3.

Distance parameter depending on incidence wave

식 (12)와 식 (13)의 g⁺와 g^-는 식 (14)와 식 (15)와 같이 구할 수 있다[6]-[8].

$\[ g^{+}=1+\cos \left(\left(\varphi \mp {\varphi }^{\text{'}}\right)-2n\pi N^{+}\right) \]$

(14)

$\[ g^{-}=1+\cos \left(\left(\varphi \mp {\varphi }^{\text{'}}\right)-2n\pi N^{-}\right) \]$

(15)

여기서 N⁺, N^-는 각각 $$ 2n\pi N^{+}-\left(\varphi \mp {\varphi }^{\text{'}}\right)=+\pi 2n\pi N^{-}-\left(\varphi \mp {\varphi }^{\text{'}}\right)=-\pi $$를 가장 잘 만족하는 양의 정수, 음의 정수 또는 0을 선택한다[6]-[8].

식 (12)와 식 (13)의 F(X)는 Fresnel transition function으로써 계산 속도의 향상을 위하여 식 (16) 및 식 (17)과 같은 근사식을 사용한다[6]-[8].

(16)

$\[ \begin{array}{c}F\left(X\right)\simeq \left(1+j\frac{1}{2X}-\frac{3}{4}\frac{1}{X^2}-j\frac{15}{8}\frac{1}{X^3}+\frac{75}{16}\frac{1}{X^4}\right)\hfill \\ \left(X>5.5\right)\hfill \end{array} \]$

(17)

여기서 0.3 < X < 5.5 구간의 경우는 내삽법을 사용하여 구한다[6]-[8]

Ⅲ. 시뮬레이션

본 논문에서 사용한 방법의 정확성을 확인하기 위하여 표 4와 같은 마스트에 대하여 UTD 계산을 수행하고 상용 전자기 해석 S/W인 FEKO[10, 11]와의 비교를 수행하였다. 주파수는 1GHz에서 10GHz의 범위를 계산 하였다. FEKO 시뮬레이션에서 송신 안테나는 헤르쯔 다이폴을 사용하였으며 송신 전력은 그림의 캡션에 제시된 P [W]로 스케일링 하였다. 송신 및 수신 안테나의 위치는 그림의 캡션에 제시된 위치벡터 T와 R로 설정하였다. 또한 헤르쯔 다이폴의 전류 방향 벡터는 $$ \vec{N}=\vec{U}\times \vec{V}$$이며 $$ \vec{U}={\left[0.3162,\mathrm{ }0,-0.9486\right]}^{\mathrm{T}},\mathrm{ }\vec{V}={\left[0, 1, 0\right]}^T$$으로 설정 하였다.

Table 4.

Vertex of mast used in simulation

그림 4는 표 4에서 정의된 표적에 대한 회절파 계산을 본 연구팀이 작성한 UTD 코드와 상용 전자파 수치해석 S/W인 FEKO의 UTD 기능을 사용하여 각각 계산하고 그 결과를 비교한 것이다.

Fig. 4.

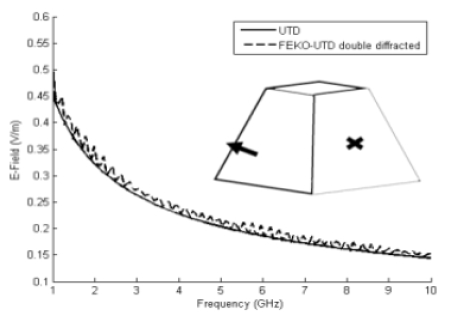
Comparison of results for the developed code and FEKO (P=0.5, T=[2.6504,0,1.3650], R=[0,1.6504,1.3650])

그림 4로부터 FEKO에서 지원하는 2차 회절의 계산 결과와 본 연구팀이 개발한 코드의 계산 결과가 거의 완전하게 일치함을 확인할 수 있다. 또한 그림 5와 6은 동일한 시뮬레이션을 P, T, R 파라미터를 바꾸어 가며 수행한 결과이다.

Fig. 5.

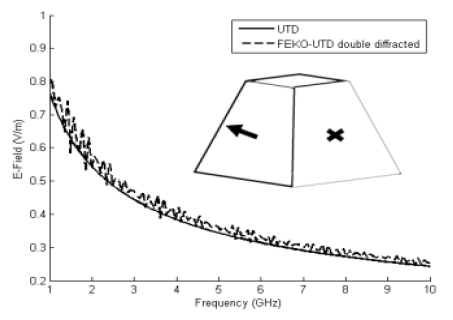
Comparison of results for the developed code and FEKO (P=1, T=[1.6504,0,1.3650], R=[0,1.6504,1.3650])

그림 5와 그림 6에서 송신 전계의 강도와 안테나의 위치가 변화하였음에도 FEKO와 개발된 코드의 계산 결과가 일치하였다. 그림 4, 5, 6에서 같은 전력을 송신할 떄 주파수가 증가함에 따라 수신점의 전계 강도가 감소하는 경향을 확인할 수 있었다.

Fig. 6.

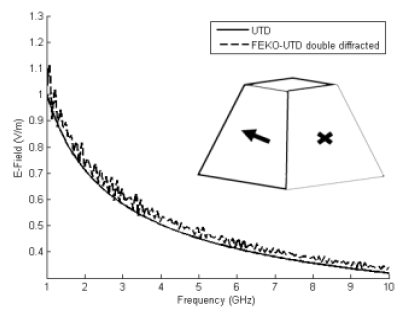
Comparison of results for the developed code and FEKO (P=1, T=[1.6504,0.5,1.3650], R=[0,1.6504,1.3650])

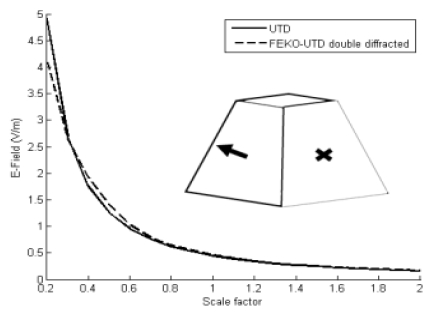
그림 7은 동일한 형상에 대하여 주파수를 3GHz로 고정하고 마스트의 크기를 바꾸어 가며 시뮬레이션을 수행한 결과이다. 크기가 변화한 마스트의 각 점들의 위치벡터는 P₁, P₂, P₃, P₄, T, R에 각각 스케일 상수(Scale factor)를 곱하여 계산하였다. 그림 7로부터 마스트의 크기가 커질수록 수신기로 들어오는 회절 성분의 크기가 작아짐을 확인할 수 있었으며 표적의 크기가 변화할 때도 개발된 코드와 FEKO의 결과가 잘 일치함을 확인할 수 있었다

Fig. 7.

Comparison of results according to target size change at 3GHz (P=1, T=[1.6504,0,5.3650], R=[0,1.6504,1.3650])

Ⅴ. 결 론

본 논문에서는 임의의 통합마스트를 가정하여 그 형상과 송수신기의 위치를 모델링하고 UTD를 계산하기 위한 코드를 개발하여 회절에 의한 수신점의 전계를 계산하였다. 또한 계산한 결과를 상용 전자파 수치해석 S/W인 FEKO의 계산 결과와 비교하여 그 정확성을 확인 하였다. 또한 통합 마스트 모델의 크기를 변화시켜가면서 통합마스트의 크기가 안테나 사이의 커플링에 미치는 영향을 분석하였다. 현재까지 연구된 결과를 바탕으로 향후에는 좀 더 현실적인 형상의 통합마스트를 분석하는 연구를 진행할 것이다.

Acknowledgments

본 연구는 국방과학연구소의 지원(계약번호:UD170002DD)을 받아 수행하였으며, 이에 감사드립니다.

References

• W. N. Dawber, et al. , "Integrated Antenna Architecture for High Frequency Multifunction Naval Systems", in 2006 CIE International Conference on Radar, Shanghai, China, p1-5, Oct.), (2006. [https://doi.org/10.1109/icr.2006.343284]
• H. Shin, et al. , "Analysis of Radar Cross Section of a Battleship Equipped with an Integrated Mast Module Based on PO and PTD", Journal of Electromagnetic Engineering and Science, 17(4), p238–-240, Oct.), (2017. [https://doi.org/10.26866/jees.2017.17.4.238]
• X. Cheng, H. Yan, and Y. Hu, "Electromagnetic interference analysis of integrated radar antennas on stealth mast", in 2015 7th Asia-Pacific Conference on Environmental Electromagnetics (CEEM), Hangzhou, China, p304-308, Nov.), (2015. [https://doi.org/10.1109/ceem.2015.7368691]
• B. Turetken, F. Ustuner, E. Demirel, and A. Dagdeviren, "EMI/EMC Analysis of Shipboard HF Antenna by Moment Method", in 2006 International Conference on Mathematical Methods in Electromagnetic Theory, Kharkov, Ukraine, p350-352, Jun.), (2006. [https://doi.org/10.1109/mmet.2006.1689789]
• Chang-hoe Kim, Jae-hoon Jung, Seong Ro Lee, Seong-Cheol Kim, "User-Body Shadowing Analysis Technique in Ship Environment Based on the Uniform Geometrical Theory of Diffraction", The Journal of Korean Institute of Communications and Information Sciences, 39(11), p1209-1215, Nov.), (2014. [https://doi.org/10.7840/kics.2014.39c.11.1209]
• R. G. Kouyoumjian, and P. H. Pathak, "A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface", Proceedings of the IEEE, 62(11), p1448-1461, Nov.), (1974. [https://doi.org/10.1109/proc.1974.9651]
• C. A. Balanis, Advanced Engineering Electromagnetics, New York, Wiley, (1989).
• P. Pathak, "High frequency techniques for antenna analysis", Proceedings of the IEEE, 80(1), p44-65, Jan.), (1992. [https://doi.org/10.1109/5.119566]
• C. A. Balanis, "Antenna Theory", USA, NY, New York, Wiley, (1997).
• J. S. Jung, H. J. Kwon, I. S. Choi, Y. H. Cho, and S. W. Oh, "Improvement of Calculation Speed of NEC-2 Code Using CUDA and OpenMP", Journal of KIIT, 16(1), p79-85, Jan.), (2018. [https://doi.org/10.14801/jkiit.2018.16.1.79]
• I. H. Kim, and I. S. Choi, "Resonance Frequency Extraction of Full-scale Radar Targets Using Time-Frequency Analysis", Journal of KIIT, 15(6), p87-94, Jun.), (2017. [https://doi.org/10.14801/jkiit.2017.15.6.87]