[ Article ]

The Journal of Korean Institute of Information Technology - Vol. 16, No. 11, pp.97-103

ISSN: 1598-8619 (Print) 2093-7571 (Online)

Print publication date 30 Nov 2018

Received 28 Sep 2018 Revised 07 Nov 2018 Accepted 10 Nov 2018

DOI: https://doi.org/10.14801/jkiit.2018.16.11.97

시변 최적 유한 임펄스 응답 필터 기반 전력 신호 고조파 검출

권보규^*

*강원대학교 전기제어계측공학부

Harmonic Estimation of Power Signal Based on Time-varying Optimal Finite Impulse Response Filter

Bo-Kyu Kwon^*

Correspondence to: Bo-Kyu Kwon Dept. of Electric, Control & Instrumentation Engineering Joongang-ro, Samcheok-si, Gangwon-do, Korea, Tel.: +-10- , email: bkkwon@kangwon.ac.kr

초록

본 논문에서는 시변 최적 FIR 필터를 이용한 전력 신호의 고조파 검출 방법을 제안한다. 잡음이 고려된 전력 신호에 대해 고조파의 진폭과 위상각의 변화량이 확률적 정보로 고려된 시변 상태 방정식 모델에 대해 시변 최적 FIR 필터를 설계하여 고조파 성분을 검출한다. 제안한 검출 방법에 사용된 시변 FIR 필터는 유한 구간의 정보만을 사용하고 어떠한 초기 조건도 사용하지 않도록 설계되어 칼만 필터 기반의 검출 방법의 오차 누적에 따른 검출 성능 저하나 발산 문제를 해결할 수 있다. 또한 FIR 구조의 필터 사용을 통해 칼만 필터 대비 불확실성에 대해 보다 강인한 검출이 가능하다. 시변 최적 FIR 필터의 사용을 통해 시불변 최적 FIR 필터 기반 고조파 검출 방법 대비 보다 일반적인 해를 제공한다. 제안하는 검출 방법의 우수성을 검증하기 위해 시변 칼만 필터 및 적응 칼만 필터 기반 고조파 검출 방법과의 비교 시뮬레이션을 수행한다.

Abstract

In this paper, the estimation method for the power signal harmonics is proposed by using the time-varying optimal finite impulse response (FIR) filter. To estimate the magnitude and phase-angle of the harmonic components, the time-varying optimal FIR filter is designed for the state space representation of the noisy power signal which the magnitude and phase is considered as a stochastic process. Since the time-varying optimal FIR filter used in the proposed method does not use any priori information of the initial condition and has FIR structure, the proposed method could overcome the demerits of Kalman filter based method such as poor estimation and divergence problem. Due to the FIR structure, the proposed method is more robust against to the model uncertainty than the Kalman filter. Moreover, the proposed method gives more general solution than the time-invariant optimal FIR filter based harmonic estimation method. To verify the performance and robustness of the proposed method, the proposed method is compared with time-varying Kalman filter based method through simulation.

Keywords:

harmonic estimation, frequency domain analysis, finite impulse response, power signal

Ⅰ. 서 론

최근 컴퓨터 및 디지털 장비의 보급이 확대됨에 따라 디지털 신호 처리 기술이 대부분의 공학 분야의 기반 기술로 자리매김 하고 있다. 이러한 디지털 신호 처리에 있어 주파수 영역 해석 방법은 매우 중요한 도구로 여러 공학 분야에서 신호나 시스템의 해석을 위해 활발히 사용되고 있다.

전력 시스템에서도 전력 품질의 측정에 있어 가장 중요한 요소인 전력 신호의 고조파 성분 검출을 위해 다양한 주파수 영역 해석 방법들이 사용되고 있다[1]-[7]. 일반적으로 주파수 영역 해석을 위한 도구로 널리 활용되고 있는 푸리에 변환을 전력 신호의 고조파 검출을 위해 적용한 방법들이 많이 사용되고 있다[2]. 푸리에 변환에 기반한 방법들은 잡음이 존재하지 않고 시간에 따라 고조파 성분이 변화하지 않는 신호에 대해서는 정확한 고조파 검출이 가능하다. 하지만, 대부분의 전력 신호에는 잡음이 존재하며, 특히 시간에 따라 변화하는 진폭과 주파수를 가지는 전력 신호의 고조파의 특성으로 인해 검출 성능이 저하되는 문제점을 가진다. 이러한 문제점을 개선하기 위하여 잡음이 존재하는 전력 신호에 대해 칼만 필터를 적용한 전력 신호의 고조파 검출 방법들이 다양하게 제안되었다[3-5]. 이 방법들은 잡음이 고려된 전력 신호의 시변 고조파 성분들이 상태 변수로 정의된 시변 선형 상태 공간 모델에 대해 칼만 필터를 적용한 것으로 측정 잡음 및 시변 고조파 성분을 모두 고려할 수 있어 기존 푸리에 변환 기반 방법 대비 좋은 검출 성능을 보였다. 하지만 칼만 필터 기반의 검출 방법은 전력 신호의 상태 공간 모델의 불확실성 및 초기 조건의 불확실성으로 인해 검출 성능이 떨어지는 단점을 가졌다. 이는 초기 시점부터 검출 시점까지의 모든 정보를 활용하는 칼만 필터의 무한 임펄스 응답(IIR, Infinite Impulse Response) 구조와 전력 신호의 상태 공간 모델에서 공정 잡음으로 고려된 고조파 성분 변화량의 불확실한 확률적 정보로부터 발생된다. 초기 조건의 불확실성 및 상태 공간 모델의 불확실성은 검출 오차를 발생시키고, 이러한 검출 오차들은 칼만 필터의 IIR 구조에 의해 누적되어 검출 결과에 많은 오차들을 포함시키게 된다.

또한 IIR 구조로 인해 발생되는 칼만 필터의 느린 검출 추종 성능은 최근 급격하게 늘어나는 신재생 에너지원이나 연료전지의 전력 계통의 연결로 인해 발생되는 전력 신호의 고조파 성분이 급격한 변화에 신속히 대응할 수 없는 문제도 가진다[8].

이러한 IIR 구조에 의해 발생되는 칼만 필터 기반 검출 방법의 문제는 유한 임펄스 응답(FIR, Finite Impulse Response) 구조 필터의 사용으로 극복할 수 있다. FIR 필터는 최근의 유한 구간 내의 정보만을 활용하여 상태를 추정하기 때문에 오차 누적에 의한 검출 성능 저하 문제를 근원적으로 해결할 수 있다[7]. 특히 FIR 필터의 경우 공정 잡음이 상태 추정 결과에 미치는 영향이 이러한 IIR 구조에 의해 발생되는 칼만 필터 대비 매우 작다[10]. 따라서 FIR 필터의 적용은 전력 신호의 고조파 성분 검출 방법에 있어 모델 불확실성에 대해 강인성을 가지는 매우 적합한 필터가 될 수 있다. 또한 FIR 필터는 무편향 성질을 만족하도록 설계되어 추정된 상태가 실제 상태로 빠르게 수렴하는 특성도 가진다. 이러한 장점에도 불구하고 전력 신호의 고조파 검출에 있어 FIR 구조를 활용한 연구는 많지 않았다. [6]에서 잡음이 고려된 전력 신호를 시불변 선형 상태 방정식으로 모델링하고, 이 모델에 대해 시불변 최적 FIR 필터를 적용한 전력 신호 고조파 검출 방법이 제안되었다. 제안된 방법은 모델 불확실성에 대해 강인하고, 급격하게 변화하는 고조파 성분 검출에 있어 빠른 수렴성을 보였으나, 시불변 필터의 적용을 위해 고려된 시불변 상태 방정식 모델에서 위상각에 대한 변화를 표현하지 못하는 단점을 가졌다. 따라서 본 논문에서는 시변 위상각이 고려된 전력 신호의 시변 상태 공간 모델에 대해 시변 FIR 필터를 적용하는 고조파 검출 방법을 제안한다. 이를 위해 먼저 잡음이 고려된 전력 신호에 대해 고조파의 진폭과 위상각의 변화량을 확률적 정보로 표현한 시변 상태 방정식 모델을 도출하고, 이 모델에 대해 시변 최적 FIR 필터를 적용하여 전력 신호의 고조파 성분을 검출한다. 제안한 검출 방법에 사용된 시변 FIR 필터는 어떠한 초기 조건도 사용하지 않도록 설계되어 초기 조건의 불확실성으로부터 발생하는 오차에 대해서도 강인한 특성을 가진다. 또한 시변 최적 FIR 필터 설계 시 사용된 무편향 조건으로 인해 급격히 변화하는 고조파 성분들에 대해 빠른 수렴성도 기대할 수 있으며, 공정 잡음의 영향을 상대적으로 적게 받는 FIR 구조적 특성으로 검출 강인성도 기대할 수 있다. 특히 시변 최적 FIR 필터는 필터의 시변 행렬들을 시불변 행렬로 놓으면 시불변 FIR 필터가 되기 때문에 제안하는 검출 방법은 [6]에서 제안된 방법 대비 보다 일반적인 해를 제공할 수 있다.

본 논문의 구성을 다음과 같다. 먼저 2장에서는 잡음이 포함된 전력 신호를 시변 상태 방정식 모델로 표현하고, 이에 대한 시변 최적 FIR 필터를 설계하여 전력 신호의 고조파 성분을 검출하는 방법을 제안한다. 3장에서는 제안하는 전력 신호 고조파 검출 방법을 시변 칼만 필터 및 적응 칼만 필터 기반의 고조파 검출 방법과 비교하는 시뮬레이션을 수행하여 제안하는 방법의 성능을 평가한다. 마지막으로 4장에서는 결론에 대해 기술한다.

Ⅱ. 시변 최적 FIR 필터를 이용한 전력 신호 고조파 성분 검출

2.1 전력 신호의 상태 공간 모델링

먼저 다음과 같은 측정 잡음이 고려된 연속형 신호를 고려한다.

z t = ∑ i = 1 n A i, t cos ⁡ i w t + θ i, t + v t

(1)

여기서 i는 고조파 차수, ω=2πf, f는 기본 주파수, 그리고 A_i,t와 θ_i,t는 각각 시간 t에서 i번째 고조파 성분의 크기와 위상각이다. 또한, υ(t)는 측정 잡음으로 공분산 R_s를 가지는 영-평균 백색 가우시안 랜덤 프로세스로 가정한다.

샘플링 간격을 Δt=t_k+1-t_k로 정의하고, k번째 샘플링 시간의 시간 변수를 k=t/Δt로 정의하면, 신호 (1)을 다음과 같이 표현할 수 있다.

z k = ∑ i = 1 n A i, t cos ⁡ i w k Δ t + θ i, k + v k .

(2)

이제 상태 변수 x_k를 고조파 성분의 크기와 위상각을 포함하도록 다음과 같이 정의하고

x k = x 1, k x 2, k ⋮ x 2 n - 1, k x 2 n, k = A 1, k cos ⁡ θ 1, k A 1, k sin ⁡ θ 1, k ⋮ A n, k cos ⁡ θ n, k A n, k sin ⁡ θ n, k,

(3)

상태 변수 x_k가 무작위 행보를 따른다고 가정하면 다음과 같은 상태 방정식을 얻을 수 있다.

x k + 1 = x k + w k,,

(4)

여기서 ω_k는 고조파 성분의 변화량으로 공분산 Q_s인 영-평균 랜덤 가우시안 프로세스로 가정한다.

신호 (3)에 대해 출력 방정식은 다음과 같은 과정으로 구할 수 있다.

z k = ∑ i = 1 n cos ⁡ i w k Δ t A i, k cos ⁡ θ i, k - sin ⁡ i w k Δ t × A i, k sin ⁡ θ i, k + υ k = cos ⁡ w k Δ t - sin ⁡ w k Δ t ⋯ cos ⁡ n w k Δ t - sin ⁡ n w k Δ t x k + υ k .

(5)

식 (3), (4)의 두 행렬을 다음과 같이 정의하면,

Φ = I n × n,

(6)

H k = cos ⁡ w k Δ t - sin ⁡ w k Δ t ⋯ cos ⁡ n w k Δ t - sin ⁡ n w k Δ t

(7)

신호 (2)를 다음의 상태 공간 모델로 표현할 수 있다.

x k + 1 = Φ x k + w k,

(8)

y k = H k x k + υ k .

(9)

여기서 고조파 성분의 크기 및 위상각의 변화량을 가우시안 랜덤 프로세스로 가정한 ω_k는 실질적 문제에 있어 알기가 매우 어렵기 때문에 이로부터 발생되는 시스템의 불확실성이 매우 커지게 되며, 이에 대한 강인한 고조파 검출 방법이 필요하다. FIR 필터는 공정 잡음에 대해 칼만 필터 대비 보다 강인한 특성을 가지므로[6], 본 논문에서는 시변 상태 공간 모델 (8)과 (9)에 대해 시변 최적 FIR 필터를 적용한 전력 신호 고조파 검출 방법을 제안한다.

2.2 시변 최적 FIR 필터를 이용한 고조파 검출

시변 선형 상태 공간 모델 (8)과 (9)에 대한 시변 최적 FIR 필터는 유한 이동 구간 [k-N k]에서 다음과 같은 구조를 가지도록 설계되며,

x k^= ∑ i = k - N k - 1 h k - i, k y i

(10)

여기서 $x^k$ 는 시간 k에서 추정된 상태, N은 유한 이동 구간의 크기이다. 그리고 y_i와 h_k-i,k는 각각 유한 이동 구간 내 i번째 측정치와 유한 임펄스 응답이다. 이제 유한 이동 구간의 측정치 벡터와 필터 이득 행렬을 다음과 같이 정의하면,

Y k - 1 = y k - N T ⋯ y k - 1 T T, H k = h N, k ⋯ h 1, k,

시변 최적 FIR 필터는 다음과 같은 행렬식으로 나타낼 수 있다.

x k^= H k Y k - 1 .

(11)

이제 비편향 조건 $E x k = E x k^$ 를 만족하고, 추정 오차의 공분산을 최소화 시키는 시변 최적 FIR필터 이득 행렬 H_k은 다음과 같은 과정으로 설계할 수 있다.

먼저 공정 잡음 ω_k의 공분산 행렬과 측정 잡음 υ_k의 k 시간의 공분산 행렬은 각각 Q_k와 R_k로 정의된 다음의 시변 선형 상태 공간 모델에 대해

x k + 1 = A k x k + G k w k,

(12)

y k = C k x k + υ k,

(13)

시변 최적 FIR 필터의 최적 이득 행렬 H_k는 다음과 같이 설계된다[7].

H k = L k - 1, k - N M k × C k T ¯ Π ¯ k - 1 C k ¯ - 1 C k T ¯ Π ¯ k - 1 Q N, K G k T ¯ Π ¯ k - 1 I - C k ¯ C k T ¯ Π ¯ k - 1 C k T ¯ - 1 C k T ¯ Π ¯ k - 1

(14)

식 (14)에서 사용된 각 행렬들은 다음과 같다.

L i, j = A i A i - 1 ⋯ A j + 1 A j i ≥ j M k = L k - 1, k - N G k - N ⋯ L k - 1, k - 1 G k - 2 G k - 1 G k ¯ = 00 ⋯ 00 C k G k - N 0 ⋯ 00 C k L k - N + 1, k - N + 1 G k - N C k G k - N + 1 ⋯ 00 ⋮ ⋮ ⋮ ⋮ ⋮ C k L k - 2, k - N + 1 G k - N C k L k - 2, k - N + 2 G k - N + 1 ⋯ C k G k - 2 0, C k ¯ = C k C k L k - N, k - N C k L k - N + 1, k - N ⋮ C k L k - 2, k - N, Q N, k = Q k - N 00 ⋯ 0 0 Q k - N + 1 0 ⋯ 0 ⋮ ⋮ ⋱ ⋯ ⋮ 000 ⋯ Q k - 1, R N, k = R k - N 00 ⋯ 0 0 R k - N + 1 0 ⋯ 0 ⋮ ⋮ ⋱ ⋯ ⋮ 000 ⋯ R k - 1, Π ¯ k = G ¯ k Q N, k G ¯ k T + R N, k

이제 A_k→Φ, G_k→I_n×n, C_k→H_k, Q_k-i→Q, 그리고 R_k-i→R로 놓으면, 신호 (2)에 대한 시변 최적 FIR 필터는 다음과 같이 설계할 수 있다.

H k = I + Q N, k G N, k Π k - 1 - Q N, k G N, k Π k - 1 C N, k × C N, k T Π k - 1 C N, k - 1 C N, k Π k - 1

(15)

여기서 $Π k = G N, k Q N G N, k T + R N$ , Q_N=diag(Q_s), R_N=diag(R_s)이고, diag( • )는 대각행렬을 의미한다. 그리고 C_N,k와 G_N,k는 각각 다음과 같다.

C N, k = C k ⋮ C k, G N, k = 00 ⋯ 00 C k 0 ⋯ 00 ⋮ ⋮ ⋮ ⋱ ⋮ C k C k ⋯ C k 0 .

이제 신호 (2)의 검출된 고조파 성분의 크기와 위상각은 추정 상태 $x^k$ 로부터 각각 다음과 같이 구할 수 있다.

A^i, k = x^2 n - 1, k 2 + x^2 n, k 2, θ^i, k = tan - 1 ⁡ x^2 n, k x^2 n - 1, k .

Ⅲ. 시뮬레이션

이 장에서는 제안하는 전력 신호 고조파 검출 방법의 우수성을 입증하기 위해 시변 칼만 필터 및 적응 칼만 필터[8] 기반 검출 방법과의 비교 시뮬레이션을 수행한다. 제안한 검출 방법에서 사용된 시변 최적 FIR 필터는 설계 시 사용된 무편향 조건에 의해 빠른 수렴성을 가질 수 있고, 또한 공정 잡음의 영향을 적게 받아 모델 불확실성에 대해 강인성을 가질 수 있다. 따라서 제안하는 방법의 빠른 수렴성에 대한 검증과 공정 잡음에 대한 강인성 검증으로 나누어 시뮬레이션을 수행한다.

3.1 빠른 수렴성 검증

먼저 제안하는 방법의 빠른 수렴성을 검증하기 위하여 다음과 같은 전력 신호에 대해 고려한다.

y t = a 1 t cos ⁡ w t + 80 + a 3 t cos ⁡ 3 w t + a 5 t cos ⁡ 5 w t + 45 + 0.02 cos ⁡ 7 w t - 40 + 0.01 cos ⁡ 11 w t + 30 + υ t

(16)

여기서 a₁(t), a₅(t), 그리고 a₅(t)는 시변 고조파 성분의 급격한 변화를 반영하기 위한 것으로 각 시간 구간에 대해 다음과 같이 설정한다.

a 1 t = 2.5, a 3 t = 0.75, a 5 t = 0.6 150 < t < 299 a 1 t = 3, a 3 t = 0.9, a 5 t = 0.7 300 < t < 449 a 1 t = 2.5, a 3 t = 0.75, a 5 t = 0.6 450 < t < 599 a 1 t = 2, a 3 t = 0.6, a 5 t = 0.475 e l s e

이제 제안하는 방법의 빠른 수렴성을 검증하기 위해 적응 칼만 필터 기반의 검출 방법과의 비교 시뮬레이션을 수행한다. 적응 칼만 필터는 추정 오차의 정보를 피드백한 필터 이득 행렬을 다음 상태 추정에 사용하여 빠른 수렴성을 보이며, 이를 적용한 전력 신호 고조파 성분 검출 방법 또한 빠른 수렴성을 가지게 된다.

다음 그림 1~3은 각각 기본 주파수 및 각 고조파 성분들에 대해 적응 칼만 필터 기반의 검출 방법과 제안한 방법의 검출 결과를 보인다.

Fig. 1.

Estimated magnitudes of fundamental freq.

Fig. 2.

Estimated magnitudes of 3rd, 5th harmonics

Fig. 3.

Estimated magnitudes of 3rd, 5th harmonics

이 결과에서 두 방법 모두 고조파 성분의 급격한 변화 직후에는 우수한 수렴 성능을 보이나 검출 오차가 일정 값 이하로 작아지는 구간에서 적응 칼만 필터 기반의 방법은 IIR 구조와 작아진 검출 오차에 의해 서서히 수렴하는 반면, 제안하는 방법은 FIR 필터의 무편향 성질에 의해 유한 구간 이내에 빠르게 수렴하는 것을 확인할 수 있다.

3.2 모델 불확실성에 대한 강인성 검증

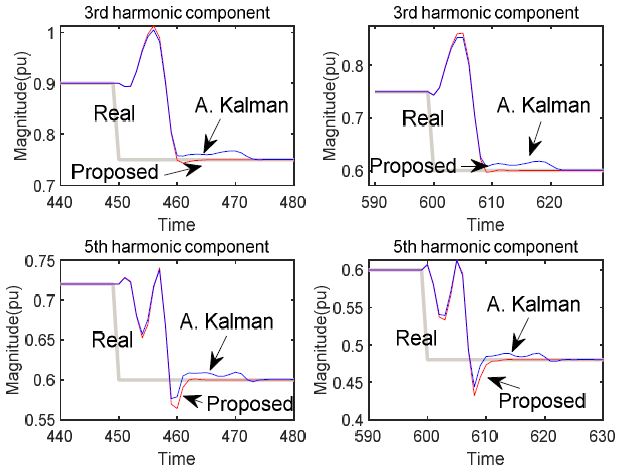
전력 신호의 상태 공간 모델 표현 과정에서 공정 잡음으로 고려된 고조파 성분의 변화량의 확률적 정보를 정확히 알기 어려우며, 이러한 부정확한 공정 잡음의 확률적 정보는 모델의 불확실성을 만들기 때문에 검출 오차를 발생시킨다. 따라서 전력 신호의 고조파 성분 검출에 있어 공정 잡음에 대한 강인성 검증이 필요하다. 이를 위해 공정 잡음의 공분산 행렬의 다양한 변화에 따른 제안한 방법과 시변 칼만 필터 기반 방법의 검출 결과와 비교한다.

이러한 시뮬레이션을 위해 신호 (16)의 a₁(t)을 시간 구간 200<t<299에서 2.5, 이 외 구간에서는 1.5가 되도록 설정한다. 또한 a₅(t)와 a₅(t)는 각각 0.15와 0.08의 상수계수가 되도록 설정한다. 또한 공정 잡음 공분산 행렬의 다양한 변화를 위하여 Q_s, Q_s/2, 그리고 Q_s/4로 설정하여 제안하는 방법과 시변 칼만 필터 기반 방법의 결과를 비교한다.

그림 4는 공분산 행렬 Q_s의 변화에 따른 제안하는 방법과 시변 칼만 필터 기반 방법의 기본 주파수 진폭 검출 결과이다. 이 결과를 살펴보면 제안하는 방법의 검출 결과는 Q_s의 큰 변화에도 검출 결과의 변화가 거의 없는 반면 시변 칼만 필터 기반 방법의 검출 결과는 Q_s의 변화에 따라 검출 오차가 크게 증가하고 매우 느리게 수렴하는 것을 확인할 수 있다. 이 결과로부터 제안하는 방법이 시스템 불확실성에 대해 칼만 필터 기반 방법 대비 강인성을 가지는 것을 확인할 수 있다.

Fig. 4.

Estimated magnitudes of fundamental freq. with various Qs

이상의 시뮬레이션 결과를 통해 전력 신호의 고조파 성분 검출에 있어 IIR 구조 필터의 적용 보다 FIR 구조 필터의 적용이 더 적합함을 알 수 있다.

Ⅳ. 결 론

본 논문에서는 잡음을 고려한 전력 신호에 대해시변 최적 FIR 필터를 이용한 고조파 검출 방법을 제안하였다. 제안된 방법에서는 잡음이 고려된 전력 신호에 대한 시변 상태 공간 모델을 도출하고, 이 모델에 대한 시변 최적 FIR 필터를 설계하여 고조파 성분을 검출하였다. 제안된 방법에서 사용한 시변 최적 FIR 필터는 최근의 유한 구간 내의 정보만을 활용하여 검출을 하기 때문에 칼만 필터 기반의 방법의 오차 누적에 의한 검출 성능 저하 문제를 근원적으로 해결할 수 있으며, 어떠한 초기 조건도 사용하지 않아 초기 조건의 불확실성으로부터 발생하는 오차에 대해서도 강인한 특성을 가진다. 또한 제안된 방법의 시변 최적 FIR 필터는 무편향 성질을 만족하도록 설계되어 검출 결과가 빠른 수렴성을 가진다. 특히 전력 신호의 상태 공간 모델은 공정 잡음에 대한 불확실성이 항상 존재하기 때문에 이에 대한 강인한 검출 방법이 필요하며, 시변 최적 FIR 필터는 칼만 필터 대비 상대적으로 공정 잡음의 영향을 적게 받기 때문에 전력 신호의 고조파 검출에 있어 시변 최적 FIR 필터의 적용이 더 적합하다고 할 수 있다. 이와 같은 제안한 방법의 우수성은 칼만 필터 및 적응 칼만 필터 기반의 검출 방법과의 비교 시뮬레이션을 통해 검증하였다.

마지막으로 잡음이 고려된 전력 신호에 대한 상태 공간 모델은 고조파 성분의 진폭과 위상각의 변화량이 모두 고려되었으며, 마지막으로 시변 최적 FIR 필터는 필터의 시변 행렬들을 시불변 행렬로 놓으면 시불변 FIR 필터가 되기 때문에 제안하는 검출 방법은 기존 시불변 FIR 필터 기반의 방법 대비 보다 일반적인 해를 제공하는데도 의의가 있다.

References

P. K. Ray, P. S. Puhan, and G. Panda, "Real-time harmonics estimation of distorted power system signal", Int. J. Electr. Power Energy Syst, 75, p91-98, Feb), (2016. [https://doi.org/10.1016/j.ijepes.2015.08.017]
IEC Std, 61000-4-7: General guide on harmonics and inter harmonics measurements and instrumentation for power supply systems and equipment connected thereto, (2009).
T. Jin, Y. Chen, and R. C. C. Flesch, "A novel power harmonic analysis method based on Nuttall-Kaiser combination window double spectrum interpolated FFT algorithm", Journal of Electrical Engineering, 68(6), p435-443, Nov), (2017. [https://doi.org/10.1515/jee-2017-0078]
S. K. Singh, N. Sinha, A. K. Goswami, and N. Sinha, "Several variants of Kalman Filter algorithm for power system harmonic estimation", Electrical Power and Energy Systems, 78, p793-800, Jun), (2016. [https://doi.org/10.1016/j.ijepes.2015.12.028]
C. I. Chen, G. W. Chang, R. C. Hong, and H. M. Li, "Extended real model of Kalman filter for time-varying harmonics estimation", IEEE Transactions on Power Delivery, 25, p17-26, Jan), (2010. [https://doi.org/10.1109/tpwrd.2009.2035217]
B. K. Kwon, S. Han, and K. Y. Lee, "Robust Estimation and Tracking of Power System Harmonics Using an Optimal Finite Impulse Response Filter", Energies, 11, p1811, Jul), (2018. [https://doi.org/10.3390/en11071811]
B. K. Kwon, "A Time-varying Optimal Finite Impulse Response Filter Based Estimation of Short-time Fourier Coefficients", Journal of Institute of Control, Robotics and Systems (in Korean), 24(1), p6-11, Jan), (2018. [https://doi.org/10.5302/j.icros.2018.17.0201]
R. G. Reddy, S. Nakka, and S. K. Sonam, "Estimation Of Power Harmonics Using Kalman Filter", International Journal for Research in Applied Science and Engineering Technology, 5(6), p1251-1257, Jun), (2017.
B. K. Kwon, S. Han, and S. Han, "Improved Receding Horizon Fourier Analysis for Quasi-periodic Signals", Journal of Electrical Engineering and Technology, 12(1), p378-384, Jan), (2017. [https://doi.org/10.5370/jeet.2017.12.1.378]

저자소개

권 보 규 (Bo-Kyu Kwon)

2002년 2월 : 인하대학교 전자공학과(공학사)

2005년 2월 : 서울대학교 전기컴퓨터공학부(공학석사)

2008년 2월 : 서울대학교 전기컴퓨터공학부(공학박사)

2008년 2월 ~ 2010년 8월 : 삼성중공업 산업기술연구소 책임연구원

2008년 2월 ~ 현재 : 강원대학교 전기제어계측공학부 교수

관심분야 : 추정이론, 신호처리, 로봇 및 제어시스템