구조 인식 심층 합성곱 신경망 기반의 영상 잡음 제거
초록
스마트폰의 보급이 확산되고 대중화됨에 따라 대부분의 사람들은 사진을 촬영하기 위해 모바일 카메라를 애용하고 있다. 하지만 저조도 환경에서 사진을 촬영할 때 광량이 부족한 이유로 원치 않는 잡음이 발생할 수 있다. 이런 잡음을 제거하기 위해, 최근 심층 합성곱 신경망에 기반한 잡음 제거 기법이 제안되었다. 이 기법은 성능 측면에서 큰 진전을 보였을지라도 여전히 텍스처 및 에지 표현 능력이 부족하다. 따라서 본 논문에서는 영상의 구조를 향상시키기 위해 에지의 방향 정보를 나타내는 호그 영상을 활용하고자 한다. 그리고 잡음 영상과 호그 영상을 스택으로 쌓은 후, 입력 텐서를 형성하여 심층 합성곱 신경망을 학습시키는 기법을 제안하고자 한다. 실험 결과를 통해, 제안한 기법은 기존의 기법보다 정량적인 화질 평가에서 더 우수한 결과를 얻을 수 있었으며 시각적인 측면에서도 텍스처 및 에지의 향상을 달성할 수 있었다.
Abstract
With the popularity of smartphones, most peoples have been using mobile cameras to capture photographs. However, due to insufficient amount of lights in a low lighting condition, unwanted noises can be generated during image acquisition. To remove the noise, a method of using deep convolutional neural networks is introduced. However, this method still lacks the ability to describe textures and edges, even though it has made significant progress in terms of visual quality performance. Therefore, in this paper, the HOG (Histogram of Oriented Gradients) images that contain information about edge orientations are used. More specifically, a method of learning deep convolutional neural networks is proposed by stacking noise and HOG images into an input tensor. Experiment results confirm that the proposed method not only can obtain excellent result in visual quality evaluations, compared to conventional methods, but also enable textures and edges to be improved visually.
Keywords:
image denoising, deep convolutional neural networks, feature extraction, image filteringⅠ. 서 론
디지털 카메라와 스마트폰 카메라 등이 보편화됨에 따라, 일상생활에서 쉽게 디지털 영상을 획득할 수 있게 되었다. 하지만 저조도 촬영환경, 양자의 불규칙성, 전송과정에서의 신호간섭 및 증폭 등과 같은 다양한 원인에 의해 영상에서 잡음이 발생하고 있다. 이러한 잡음은 영상의 화질을 저하시키는 결정적인 요소 중 하나이다. 잡음의 종류에는 잡음의 특성과 분포에 따라서 임펄스 잡음, 가우시안 잡음, 푸아송 잡음 등으로 구분할 수 있다[1]. 일반적으로 디지털 카메라로 촬영된 사진에서의 잡음은 가우시안 확률분포로 모델링이 된다.
영상의 잡음 제거란 사진의 품질을 떨어뜨리는 잡음을 제거하고, 고선명 영상을 복구하는 과정을 말한다. 기존의 영상 잡음 제거 기법은 각 채널에 가우시안 필터[2], 쌍방향 필터(Bilateral Filter)[3], 비국부 평균 필터(NonLocal-Means Filtering)를 적용하거나[4], 에지의 통계적 특성 분포, 예를 들면 스팔스(Sparse)한 제약 조건을 설정하여 잡음을 제거하는 기법이 있다[5]. 최근에는 심층 신경망(Deep Neural Networks)[6]이나 심층 합성곱 신경망 (Deep Convolutional Neural Networks)[7] 기법이 영상 잡음 제거 기법에 도입이 되고 있다. 이 기법들은 잡음과 원본 패치를 훈련 집합으로 사용해서 심층 신경망이나 심층 합성곱 신경망의 파라미터를 학습해서 잡음 영상을 원본 영상으로 사상한다. 이 기법들은 종래의 영상 제거 기법보다 성능 측면에서 상당한 개선을 했지만, 영상 구조(Image Structures)에 따른 패치의 구분 없이 전역적으로 학습하기 때문에 에지를 표현할 수 있는 능력이 떨어질 수 있다.
따라서 본 논문에서는 앞서 언급한 문제점을 개선하기 위해 잡음 영상과 에지의 방향에 따른 크기 성분을 나타내는 호그(HOG, Histogram-of-Oriented Gradients)[8] 영상을 심층 합성곱 신경망의 입력으로 주어 학습하는 기법을 제안하고자 한다. 기존의 심층 합성곱 신경망과 달리, 호그 영상을 잡음 영상과 함께 사용함으로써 학습이 진행되는 동안에 에지의 방향 및 텍스처의 정보를 활용하여 영상 구조 표현에 좀 더 효과적인 학습을 유도할 수 있다. 본 논문에서는 심층 합성곱 신경망을 학습하기 위해, 전체 영상이 아닌 패치 기반으로 심층 합성곱 신경망의 파라미터를 추정할 것이다. 그리고 객체의 스케일에 보다 불변한 성능을 유지하거나 보다 풍부한 훈련 데이터를 확충하기 위해 입력 영상을 스케일별로 추출하고자 한다.
본 논문의 구성은 다음과 같다. 먼저 제 2장에서는 기존의 잡음 영상 제거 기법에 대해 소개한 후, 제 3장에서는 제안한 기법을 자세히 설명하고자 한다. 특히 에지의 방향에 따른 크기 성분을 나타내는 호그 기반의 심층 합성곱 신경망 학습 과정에 대해 소개하고자 한다. 제 4장에서는 제안한 기법을 기존의 방법과 비교 분석하고, 마지막 제 5장에서는 결론 및 향후 연구에 대해 고찰하고자 한다.
Ⅱ. 관련 연구
2.1 필터링 기반의 잡음 제거 기법
가장 고전적인 영상 잡음 제거 기법은 필터링 기반의 접근 방식을 취한다. 대표적인 필터링 기법은 가우시안 필터링, 쌍방향 필터, 비국부 평균 필터등이 있다. 이 중에서 가장 간단한 가우시안 필터링 기법은 다음과 같이 표현된다[2].
| (1) |
여기서 i는 현재 픽셀 위치를 나타나고 j는 i번째 픽셀의 이웃 픽셀이다. 따라서 는 두 픽셀간의 거리를 나타낸다. 그리고 Ci는 정규화 계수(Normalizing Coefficient)이고 는 가우시안 함수의 퍼짐 정도를 나타내는 분산이다. 식 (1)이 의미하는 바는 i번째 위치에서 잡음이 제거된 픽셀 값 x(i)는 이웃 픽셀들의 값, 즉 y(j)에 거리에 반비례하는 가중치를 곱한 후, 합산함으로써 표현된다. 여기서 가중치는 지수 함수로 표현된 부분에 대응하며, 픽셀 i와 픽셀 j의 거리에 반비례하도록 설정된다. 이 기법은 평탄한 영역에서 잡음을 제거할 수 있는 장점이 있지만, 에지 영역이나 평탄 영역과도 상관없이 거리에 반비례하는 값을 가중치로 사용하기 때문에 에지의 선명도가 감소할 수 있는 단점이 있다.
2.2 비국부 평균 필터링 기반 잡음 제거 기법
이 기법은 일반 영상에서 유사한 패치가 반복적으로 나타난다는 통계적 특성을 활용한다. 대부분의 영상은 모자나 사람의 윤곽처럼 유사한 에지 방향을 갖는 패치들이 존재한다는 것을 볼 수 있다. 그리고 이러한 유사 패치는 영상의 전 영역에 걸쳐 존재할 수 있기 때문에 비국부 기반의 필터링에 속한다. 따라서, 이웃 픽셀만을 고려하는 국부 필터링 기반의 가우시안 필터링과는 엄연히 차이점이 있다. 비국부 평균 필터링은 다음과 같이 표현된다[4].
| (2) |
여기서 y(Nj)와 y(Ni)는 각각 j번째, i번째 픽셀 위치에서 추출된 패치이다. 식 (2)와 식 (1)에서 차이가 나는 부분은 지수 함수에서 가중치를 계산하는 부분으로써, 비국부 필터링 기법은 가중치를 두 패치, 즉 y(Nj)와 y(Ni)가 얼마나 유사한지에 반비례하도록 설정한다. 그리고 j는 i의 이웃 픽셀이 아니라 영상 전체의 픽셀 위치이다. 즉, 비국부 기반의 필터링이다. 식 (2)에서 보듯이, 유사한 두 패치에 대해서는 y(j)의 픽셀 값에 높은 가중치를 할당하기 때문에 에지 영역에서 선명도를 유지할 수 있다. 식 (1)에서 표현된 가우시안 필터링보다 에지 표현에서 더 우수한 능력을 지닐 수 있다.
2.3 제약 조건 기반의 잡음 제거 기법
기존의 필터링 기반과는 달리, 일반 영상의 에지의 통계적 특성 분포를 제약 조건으로 설정하여 잡음을 제거하는 기법이 있다.
| (3) |
여기서 D는 원본 영상 x의 그라디언트(Gradients)를 구하기 위한 행렬이고, λ는 첫 번째 항목과 두 번째 항목에 대한 가중치를 조절하는 파라미터이다. 첫 번째 항목은 데이터 충실도 항목으로써, 우리가 찾고자 하는 원본 영상 x는 잡음 영상 y와 유사해야 된다는 제약 조건이다. 그리고 두 번째 항목은 정규화(Regularization) 항목으로써 입력 영상의 그라디언트의 값은 작아야 된다는 제약 조건이다. 입력 영상에 그라디언트 필터를 적용하면, 에지와 같은 결과를 얻기 때문에 식 (3)에서 두 번째 항목을 최소화 하는 것은 0에 가깝도록 하는 것이다. 이는 일반 영상의 밝기의 천이가 부드럽게 변한다는 특성을 반영한 것으로 해석할 수 있다. 식 (3)에서 데이터 충실도 항목과 정규화 항목 모두 유클리디언 놈(Norm)이기 때문에 다음과 같은 닫힌 해(Closed-Form Solution)가 존재한다.
| (4) |
여기서 I는 단위 행렬이다. 식 (4)는 역행렬과 행렬을 포함하고 있기 때문에 실제 구현할 때에는 주파수 영역에서 계산하는 것이 계산속도 측면에서 더 유리할 수 있다. 그리고 식 (3)에서 정규화 항목의 놈이 유클리디언 놈이 아니라, l0-놈 [9]이나 l1-놈 [5]으로 모델링될 수 있다. 이는 에지의 통계 분포가 스팔스한 특성을 지닌 것을 의미한다. 또한 주파수 영역에서 3차원 공간에서의 스팔스한 제약 특성을 모델링할 수 있다[10]. 이러한 스팔스 기반의 영상 잡음 제거 기법은 최근 스팔스 코딩(Sparse Coding)이나 사전 학습(Dictionary Learning)[9]을 통해 영상 잡음 제거에 상당한 효과가 있는 것을 보이고 있다. 더 나아가 최근에는 뉴클리어 놈(Nuclear Norm)[11]이나 놈의 값이 특정 값으로 고정된 게 아닌, 보다 풍부한 사전 확률을 다양한 필터와 함수의 합성곱(Convolution)으로 모델링한 반응 확산 모델(Reaction Diffusion Model)[12]을 이용한 잡음제거기법도 개발되고 있다.
2.4 심층 합성곱 신경망 기반 잡음 제거 기법
최근 사전 학습과 더불어 잡음 제거의 상당한 성능을 증명하고 있는 기법은 심층 학습 기반의 잡음 제거 기법이다. 심층 학습 기반의 잡음 제거 기법은 기존의 필터링 기반이나 에지의 통계 분포 모델링과는 달리, 잡음과 원본 영상으로 구성된 훈련 데이터를 사용해서 계층적인 구조로 이루어진 복잡한 노드들 간의 관계를 학습하는 기법이다. 잡음 제거를 위해 사용되는 대표적인 심층 학습 기법에는 심층 다층 신경망(Deep Multi-layer Neural Networks)[6], 심층 합성곱 신경망(Deep Convolutional Neural Networks)[7], 잔차 네트워크(Residual Network)[13]가 있다. 특히, 심층 합성곱 신경망이 영상 잡음 제거에서 탁월한 성능이 보이고 있다. 심층 합성곱 신경망은 합성곱(Convolution), 풀링(Pooling), 정류선형유닛(ReLU: Rectified Linear Unit)등으로 구성되어 있다.
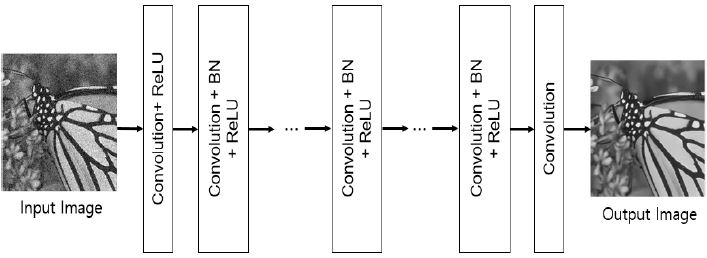
그림 1은 심층 합성곱 신경망 기반의 잡음 제거 기법을 보여주고 있다. 이 기법은 미리 학습된 심층 합성곱 신경망에 잡음 영상이 입력으로 주어지면, 합성곱, 풀링, 배치 정규화(BN, Batch Normalization), 정류선형유닛을 거친 후, 잡음이 제거된 원본 영상을 출력해준다. 하지만 심층 합성곱 신경망 기법은 출력 영상이 취할 수 있는 값의 범위가 넓기 때문에 학습시간이 오래 걸리거나 학습이 떨어질 수 있다. 이러한 단점을 보완하고자 잔차 네트워크[13] 기법이 개발되고 있다. 이 기법은 잡음 영상과 잡음 영상에서 원본 영상을 뺀 차 영상을 훈련 영상으로 사용하기 때문에 출력 계층에서 값의 범위가 기존의 심층 합성곱 신경망보다 상대적으로 적어 학습의 정확도를 좀 더 개선할 수 있다.
Ⅲ. 제안한 호그 인식 기반의 심층 합성곱 신경망 기반의 잡음 제거 기법
3.1 접근 방법
앞서 언급한 바와 같이 제안한 심층 합성곱 신경망은 에지 표현 능력 향상을 위해, 호그 영상을 추가적으로 사용하는 아키텍처를 제안한다. 따라서 제안한 호그 인식 기반의 심층 합성곱 신경망을 학습하기 위해서는, 먼저 호그 영상을 포함한 훈련 데이터베이스 수집과 호그 인식 기반의 심층 합성곱 신경망을 학습하는 단계가 필요하다. 그리고 제안한 호그 인식 기반의 심층 합성곱 신경망이 학습된 후, 입력 영상에서 호그 영상을 추정하고 잡음을 제거하는 단계가 필요하다.
◆ 1단계 (훈련 데이터베이스 수집): 제안한 심층 합성곱 신경망을 학습하기 위해, 훈련 영상으로써, 흑백 영상 400장을 인터넷에서 수집한다. 그리고 영상의 스케일에 불변한 특성을 반영하기 위해, 영상을 스케일 별로 획득한 후, 원본 패치를 추출한다. 그리고 에지의 방향에 따른 크기 성분을 히스토그램으로 표현한 호그 패치를 획득한다. 또한 원본 패치에 가우시안 잡음을 추가해서 잡음 패치를 생성한다. 추출된 패치의 크기는 40×40이다.
◆ 2단계 (심층 합성곱 신경망 학습): 제안한 호그 인식 기반의 심층 합성곱 신경망 기법은 입력 층에 잡음 영상과 호그 영상을 스택으로 쌓아서 학습을 한다. 총 학습에 사용된 레이어는 총 18개의 층으로 이루어져 있고, 자세한 아키텍처 구조는 다음 절에서 소개하도록 하겠다.
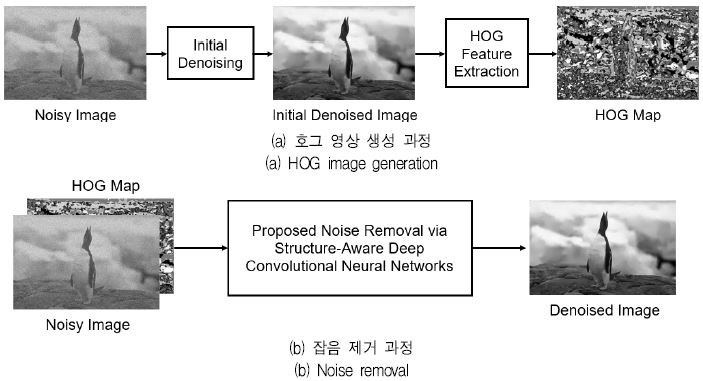
◆ 3단계 (심층 합성곱 신경망 기반의 잡음 제거): 입력 잡음 영상이 주어지면, 호그 영상을 추정하기 위해 초기 잡음 제거를 수행한다. 그리고 잡음 영상과 호그 영상을 스택으로 쌓은 다음, 미리 학습된 호그 인식 기반의 신경망을 통과하면 잡음이 제거된 영상을 얻을 수 있다. 여기서, 초기 잡음 제거 과정은 호그 영상 추정에만 사용됨을 명심하자.
3.2 호그 패치 추출
원래 호그는 컴퓨터 비전 분야에서 사용되는 수작업(Handcrafted) 기반의 특징이다[8]. 특히, 단일 영상에서 보행자 검출을 목적으로 널리 사용되고 있다. 원래 보행자 검출을 위해서 제시된 호그 특징 추출 기법은 미리 정해진 원도우 크기를 겹침이 허용되는 블록(Blocks)의 수로 분할한 뒤, 다시 각각의 블록을 셀(Cells)로 나눈 다음에 각 셀에서 에지의 방향에 대한 크기를 계산한다. 즉, 각 셀마다 히스토그램을 계산한다. 이렇게 각 셀마다 획득된 히스토그램을 블록 단위로 정규화 과정을 거친 다음, 윈도우 내의 모든 블록에서 얻은 정규화 된 히스토그램을 1차원으로 합친 것을 호그 특징이라 말한다. 이렇게 윈도우에서 추출된 히스토그램의 정보는 보행자와 배경을 구별 짓는 중요한 특징이 될 수 있다. 하지만, 본 논문에서는 보행자 검출이 아니라, 영상의 잡음을 제거하는 것이 목적이므로 원래 호그 특징 추출 기법을 그대로 따르는 것이 아니라, 셀 단위로 히스토그램을 계산하는 부분만을 사용하고자 한다.
본 논문에서 사용한 호그 특징 추출은 입력 영상이 주어지면, 래스터 스캐닝(Raster Scanning)을 하면서, 즉 8×8 크기의 원도우 창을 오른쪽에서 왼쪽, 위에서 아래로 한 칸씩 이동하면서 패치를 수집한다. 그리고 수집된 각각의 패치에 대해서, 그라디언트의 크기 및 방향을 계산한다. 입력 영상에서 (i,j)위치에서의 밝기 값을 f(i,j)라고 하면, 그라디언트의 크기 m(i,j)와 그라디언트의 방향 θ(i,j)은 다음과 같이 계산된다.
| (5) |
| (6) |
| (7) |
| (8) |
식 (5)와 (6)을 사용해서 히스토그램을 구성하기 위해, 본 논문에서 20간격으로 총 9개의 그라디언트 방향을 히스토그램 빈(Bin)으로 사용했다.
3.3 훈련 패치 데이터베이스 구축
기존의 잡음 패치와 원본 패치를 가지고 학습을 시키는 방법과는 달리, 제안한 기법은 입력으로 잡음 패치와 원본 패치를 스택으로 쌓은 데이터를 사용한다. 따라서 본 논문에서 학습에 사용되는 패치는 잡음 패치, 원본 패치, 그리고 호그 패치, 즉 3 종류의 패치가 필요하다.
먼저, 호그 패치를 획득하기 위해 본 논문에서는 잡음 영상이 아닌, 초기 잡음 제거 과정이 적용된 복원 영상에서 호그 패치를 계산한다. 왜냐하면 잡음 영상은 잡음으로 인한 정확한 에지를 계산하기 어렵기 때문이다. 물론 원본 영상에서 호그를 사용할 수 있지만, 테스트 과정에서 원본 영상을 모르기 때문에 동일한 초기 잡음 제거 기법을 적용한 복원 영상에서 호그를 추출하는 게 더 효과적일 수 있다. 다시 말하면, 초기 잡음 제거 과정이 적용된 복원 영상에서 추출된 호그 영상을 사용하여 학습하면, 테스트 과정에서도 복원 영상에서 호그 영상을 추출한 정확도를 보상해 줄 수 있을 것이다.
먼저 잡음 영상 생성을 위해, 본 논문에서는 원본 영상에 가우시안 잡음의 강도를 25로 설정해서 잡음을 생성하였다. 그리고 호그 영상을 얻기 위해, 초기 잡음 제거 기법을 잡음 영상에 적용해서 잡음이 제거된 영상을 얻는다. 그런 후에, 3.2절에서 언급한 호그 특징 추출 과정을 통해 호그 영상을 생성한다. 이 과정을 통해, 학습에 필요한 원본 패치, 잡음 패치, 호그 패치를 수집할 수 있다.
그림 2는 훈련 패치 추출 과정을 보여주고 있다. 그림의 2의 노란색 박스 영역에서 보듯이 좌에서 우로, 위에서 아래로 10칸씩 이동하면서 원본 패치를 추출한다. 또한 객체의 스케일을 보다 불변한 성능을 유지하고, 보다 풍부한 훈련 데이터를 확보하기 위해 영상의 스케일을 1, 0.9, 0.8, 0.7배의 크기로 패치를 추출한다. 그림 2의 상단에 스케일에 따른 영상을 보여주고 있다. 그리고 그림 2의 하단에 초기 잡음이 제거된 영상에서 호그 영상을 구한 예시들을 보여주고 있다. 본 논문에서 추출된 패치의 크기는 40×40이고, 학습에 사용된 총 패치의 수는 212,096개이다.
3.4 호그 인식 기반의 합성곱 신경망 학습
제안한 호그 인식 기반의 심층 합성곱 신경망의 구조는 그림 3과 같다.
먼저 그림 1에 보이는 기존의 신경망 구조와는 달리, 심층 합성곱 신경망의 입력 층에 스택으로 쌓은 잡음 패치와 호그 패치가 사용된다. 입력 층에 호그 패치를 추가적으로 사용함으로써, 학습 동안에 잡음 패치에 에지의 정보를 제공하여 에지 표현에 대한 능력을 강화할 수 있다.
제안한 호그 인식 기반의 심층 합성곱 신경망은 합성곱과 정류선형유닛 또는 합성곱, 배치정규화 및 정류선형유닛으로 구성된 한 세트가 총 18개로 구성되어 있다. 입력 층을 바로 잇는 합성곱 계층은 입력이 호그 패치와 잡음 패치로 구성된 2차원이기 때문에, 3×3×2로 이루어진 64개의 필터를 사용한다. 그리고 이후에 보이는 합성곱 계층은 64개의 3×3 필터를 사용한다. 손실 계층 바로 직전의 합성곱 계층은 3×3 필터 1개만을 사용한다. 손실 계층에서는 유클리디언 놈을 사용해서, 원본 패치와 손실 계층 바로 앞에서 추정된 잡음이 제거된 패치가 얼마나 유사함을 학습이 진행되는 동안 그 손실 정도를 평가한다.
3.5 잡음 제거 과정
제안한 호그 인식 기반의 심층 합성곱 신경망이 학습된 후, 입력 잡음 영상에서 잡음을 제거할 수 있다. 그림 4는 제안한 기법의 잡음 제거 과정을 보여준다. 먼저, 초기 잡음 제거 기법을 잡음 영상에 적용해서 호그 영상을 추정한다. 3.3절에서 언급했듯이, 학습 동안에 호그 영상을 초기 잡음 제거 기법을 적용한 결과 영상에서 추정했기 때문에 동일한 초기 잡음 제거 기법을 사용해야 된다. 호그 영상을 추정한 후, 호그 영상과 입력 잡음 영상을 스택으로 쌓은 후, 미리 학습된 심층 합성곱 신경망에 입력으로 주면 잡음이 제거된 영상이 출력된다. 다시 강조하지만, 제안한 기법은 그림 1의 기존의 방법과는 달리, 호그 인식 기반의 심층 합성곱 신경망을 학습하고, 학습된 신경망을 사용해서 잡음을 제거한다는 점에서 분명한 차이점이 있다.
Ⅳ. 실험 및 결과
4.1 실험 환경
본 논문에서는 흑백 영상 400장을 훈련 영상으로 사용하였고, 훈련 영상에 포함되지 않은 20장을 테스트 영상으로 사용하였다. 그리고 호그 영상을 추정하기 위해 초기 잡음 제거 기법으로, 기존의 심층 합성곱 신경망 기법[7]을 사용하였다.
그리고 제안한 기법의 성능을 비교 분석하기 위해, 최고의 성능을 자랑하는 3차원 공간에서의 스팔스한 제약 조건을 사용한 BM3D[10], 심층 합성곱 신경망 기법[7], 심층 다층 신경망 기법[6]을 테스트하였다. 그리고 학습에 사용된 GPU의 사양은 GTX 1080 Ti이고, 개발 언어는 매트랩이다.
4.2 실험 결과
그림 5, 6, 7은 기존 기법과 제안한 기법을 적용한 결과 영상이다. 시각적 효과를 확인하고자, 그림에서 노란색 박스 영역을 확대해서 푸른색 박스 부분에 복사하였다. 그림 5의 지붕의 라인을 살펴볼 때, 제안한 기법이 라인의 선명도를 가장 잘 표현함을 알 수 있다. 그림 6에서는 기존의 방법들은 사람의 두 팔을 모두 잘 묘사하지 못했지만, 제안한 기법은 사람의 팔을 완전히 복구한 것을 볼 수 있다. 그림 7에서도 제안한 기법이 물결과 같은 텍스처를 상대적으로 잘 표현한 것을 볼 수 있다. 특히 기존의 심층 합성곱 신경망 기법보다 에지나 텍스처의 표현 능력이 강화된 것은 호그 패치와 잡음 패치를 스택으로 쌓아 학습했기 때문이다. 즉, 기존의 심층 합성곱 신경망 기법은 잡음 패치에서 원본 패치를 추정하기 때문에 잡음 패치에서 에지 정보를 추정하기가 어렵다. 이에 반해 제안한 기법에서는 호그 영상을 사용하기 때문에 학습 동안에 에지의 추가적인 정보로 인해서 신경망의 에지나 텍스처 표현 능력을 강화할 수 있다.

Resulting images; (a) Original image, (b) Noise image, (c) Proposed noise removal via HOG-Aware deep convolutional neural networks, (d) Noise removal via deep convolutional neural networks [7], (e) Noise removal via deep multilayer neural networks [6], and (f) BM3D [10]

Resulting images; (a) Original image, (b) Noise image, (c) Proposed noise removal via HOG-Aware deep convolutional neural networks, (d) Noise removal via deep convolutional neural networks [7], (e) Noise removal via ceep multilayer neural networks [6], and (f) BM3D [10]

Resulting Images; (a) Original image, (b) Noise image, (c) Proposed noise removal via HOG-Aware deep convolutional neural networks, (d) Noise removal via deep convolutional neural networks [7], (e) Noise removal via deep multilayer neural networks [6], and (f) BM3D [10]
표 1은 정량적 평가 결과를 보여주고 있다. 본 논문에서는 최대 신호 대 잡음비(PSNR, Peak Signal–to-Noise Ratio)를 척도로 사용하였다. 표 1에서 사용된 테스트 영상들은 그림 8에 제공되어 있다. 테스트 영상은 평탄한 영역과 에지 영역을 골고루 포함되도록 선택하였다. 표 1에서 보듯이 제안한 기법이 평균치 측면에서 기존의 방법보다 0.11dB 더 우수한 결과를 얻을 수 있었다. 이 증가된 수치는 시각적인 비교를 통해, 잡음 제거 그리고 에지 표현 능력 측면에서 최소한의 감지 가능한 차이를 능가하는 값임을 알 수 있다.
Ⅴ. 결론 및 향후 과제
본 논문에서는 영상 잡음 제거를 위한 호그 인식 기반의 심층 합성곱 신경망 학습 기법을 제안하였다. 실험 결과에서 보듯이, 호그 영상을 학습 과정에 사용했을 때, 심층 합성곱 신경망이 에지나 텍스처 표현에 대한 능력을 강화할 수 있음을 확인하였다. 또한 최대 신호 대 잡음비 평가에서 기존의 방법보다 우수한 결과를 얻을 수 있었고, 시각적인 평가에서도 텍스처나 에지 영역에서 더 세밀한 표현 능력을 달성할 수 있었다.
향후 계획으로는 본 논문에서 제시된 호그 인식 심층 합성곱 신경망 구조를 개선하기 위해, 호그 영상과 잡음이 제거된 영상을 동시에 학습하는 기법을 개발하고자 한다. 현재는 호그 영상을 초기 잡음 제거 기법을 사용해서 추정해야 되는 번거로움이 있다. 따라서 향후에는 호그 영상도 동시에 추정 가능한 신경망 구조를 개발하고자 한다.
Acknowledgments
이 논문은 2017년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임 (No. 2017R1D1A3B03030853)
References
-
H. W. Lee, and S. W. Lee, "Improving image noise reduction by shapley value normalization", Journal of Korean Institute of Information Technology, 11(10), p29-34, Oct), (2013.
[https://doi.org/10.14801/kiitr.2013.11.10.29]

- M. R. Gu, K. S. Lee, and D. S. Kang, "Image noise reduction using modified gaussian filter by estimated standard deviation of noise", Journal of Korean Institute of Information Technology, 8(12), p111-117, Oct), (2010.
- C. Tomasi, and R. Manduchi, "Bilateral filtering for gray and color Images", IEEE International Conference on Computer Vision, Bombay, India, p839-846, Jan), (1998.
-
A. Buades, B. Coll, and J. M. Morel, "A non-local algorithm for image denoising", IEEE International Conference on Computer Vision and Pattern Recognition, San Diego, CA, U.S.A, p60-65, Jun), (2005.
[https://doi.org/10.1109/cvpr.2005.38]

- D. Krishnan, R. Fergus, "Fast image deconvolution using hyper-laplacian priors", Advances in Neural Information Processing Systems, p1033-1041, Dec), (2009.
-
H. C. Burger, C. J. Schuler, and S. Harmeling, "Image denoising: Can plain neural networks compete with BM3D?", IEEE Conference on Computer Vision and Pattern Recognition, RI, U.S.A, p4321-4328, Jun), (2012.
[https://doi.org/10.1109/cvpr.2012.6247952]

- V. Jain, and H. S. Seung, "Natural image denoising with convolutional networks", Advances in Neural Information Processing Systems, p769-776, Dec), (2008.
- N. Dalal, and B. Triggs, "Histograms of oriented gradients for human detection", IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1, p886-893, Jun), (2005.
-
M. Elad, and M. Aharon, "Image denoising via sparse and redundant representations over learned dictionaries", IEEE Transactions on Image Processing, 15(12), p3736-3745, Dec), (2006.
[https://doi.org/10.1109/tip.2006.881969]

-
K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, "Image denoising by sparse 3d transform domain collaborative filtering", IEEE Transactions on Image Processing, 16(8), p2080-2095, Aug), (2007.
[https://doi.org/10.1109/tip.2007.901238]

- Y. Xie, S. Gu, Y. Liu, W. Zuo, W. Zhang, and L. Zhang, "Weighted schatten p-norm minimization for image denoising and background subtraction", IEEE Transactions on Image Processing, 25(10), p4842-4857, Oct), (2016.
-
Y. Chen, W. Yu, and T. Pock, "On learning optimized reaction diffusion processes for effective image restoration", IEEE Conference on Computer Vision and Pattern Recognition, p5261-5269, Jun), (2015.
[https://doi.org/10.1109/cvpr.2015.7299163]

-
K. Zhang, W. Zuo, Y. Chen, D. Meng, and L. Zhang, "Beyond a gaussian denoiser: residual learning of deep CNN for image denoising", IEEE Transactions on Image Processing, 27(7), p3142-3155, Jul), (2017.
[https://doi.org/10.1109/tip.2017.2662206]


2019년 2월 : 군산대학교 소프트웨어융합공학과(공학사)
관심분야 : 컴퓨터 비전, 영상처리, 딥 러닝, 프로그래밍

2002년 2월 : 경북대학교 전자전기공학부(공학사)
2004년 2월 : 경북대학교 전자공학과(공학석사)
2008년 8월 : 경북대학교 전자공학과(공학박사)
2008년 8월 ~ 2009년 12월 : 삼성전자 프린팅사업부 책임연구원
2015년 3월 ~ 2017년 2월 : 캐나다 Ryerson 대학교 포닥연구원
2017년 4월 ~ 현재 : 군산대학교 소프트웨어융합공학과 조교수
관심분야 : 컴퓨터 비전, 영상처리, 기계학습, 딥 러닝