MCP 세척용 전자총 개발을 위한 컴퓨터 시뮬레이션

Ⅰ. 서 론

MCP(Micro-Channel Plate)는 단일 입자(전자, 이온 및 중성자)와 저강도의 방사선(자외선 및 X선)의 검출에 사용되는 전자증폭기이다. 구조는 내경 5~20㎛의 매우 미세한 유리관(채널)을 수백만개 묶어서 두께 1~2㎜정도의 원판모양으로 만들어져 있고, 각 유리관 내벽은 2차전자 방출재료로 코팅되어 있다. 입사입자가 유리관에 들어오게 되면 유리관 내벽과 충돌하면 2차전자를 생성하게 되는데, 입사입자와 유리관의 충돌을 용이하게 하기 위하여 유리관은 입사입자의 방향과 약 8^o정도 기울어져 있다. 원판의 양면에 전압을 인가하면 입사입자 대비 10³~10⁵배의 gain을 얻을 수 있고, 두 개의 MCP를 겹친 적층형(Tandem Type)은 10⁶~10¹⁰배의 이득을 얻을 수 있다. 각각의 유리관은 독립적으로 증폭하면서, 직경이 매우 작고 증폭율이 매우 높기 때문에, 단일입자의 검출용, 야시경과 같은 이미지 센서(Imaging Detector)및 위치센서(Position Sensitive Detector) 등 다양하게 활용되고 있다[1]-[3].

MCP의 제작공정에서, 직경 5~20㎛의 미세한 유리관 내부를 세척하는 과정이 필요한데, 이때 세척 방법 중 하나가 전자빔을 이용하는 것이다. MCP 세척용으로 사용하는 전자총은 원하는 거리(전자총과 MCP까지의 거리) 및 원하는 면적(MCP의 면적)내에서 전자빔의 밀도가 균일하도록 만들어져야 한다. 본 연구의 목적은 MCP의 제작공정에서 MCP 세척용 전자총을 개발하기 위한 사전 단계로서, SIMION 프로그램을 이용하여 전자의 궤적을 컴퓨터 시뮬레이션하여 전자총 설계를 위한 최적조건을 찾는 것이다.

Ⅱ. 컴퓨터 시뮬레이션

2.2 컴퓨터 시뮬레이션 조건

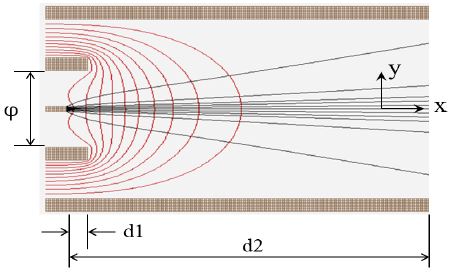
그림 1(a)는 전자총과 MCP의 배치를 보여주기 위한 블럭도이고, (b)는 SIMION 프로그램으로 컴퓨터 시뮬레이션하기 위하여 각 부분의 구조를 기호로 정의한 것이다. 그림 1(b)에서, S는 전자 방출원이고, E는 익스트랙터(Extractor), 그리고 T는 전자총을 싸고 있는 튜브로서 1.33" CF 플랜지가 연결되어 있는 포터이다. 표적은 MCP의 위치를 대신한 것으로 전자가 도달하는 위치를 표시한 것이다. 익스트랙터에 걸린 전압은 V, 익스트랙터의 직경은 ϕ, 전자방출원과 익스트랙터 관 끝까지의 간격은 d1, 전자방출원과 쳄버 벽까지의 간격은 d2로 정의하였다. 여기서 전압 V는 전자가 표적에 도달했을 때의 에너지 E가 되기 때문에, 이하에서는 V대신 E로 대신하였다.

Fig. 1.

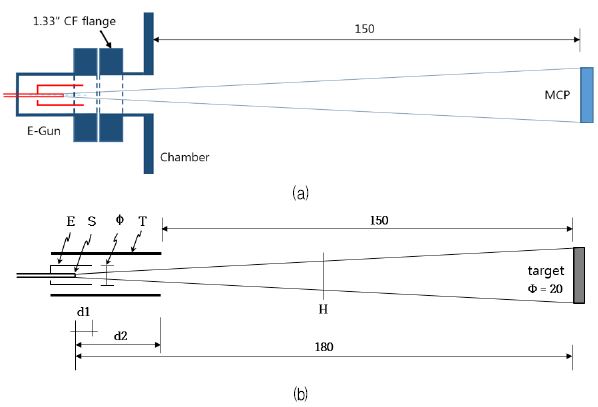
(a) Block diagram of electron gun, (b) Definition of notations for computer simulation on the SIMION program

T의 직경은 1.33“CF 플랜지가 고정되어 있는 포터이기 때문에 14mm로 고정하였고, 전자방출원에서 MCP까지의 거리는, MCP 세척 환경(전자총의 제원 및 쳄버의 크기 등)에 맞추어 180mm로 두었다. 세척하고자 하는 MCP의 직경이 약 20mm이기 때문에, 위에서 정의한 E, ϕ, d1, d2, 4개의 변수를 이용하여, 표적에 도달하는 전자의 빔직경이 20mm가 되는 조건을 찾았다. 전자를 방출하는 전자방출원은 코일형태로 된 필라멘트이지만 컴퓨터 시뮬레이션 프로그램상의 제약으로 직경 1mm인 원판형으로 가정하였고, 전자방출원과 익스트랙터에 걸리는 전압은 동등하게 인가하였다.

표적에 도달하는 전자빔의 직경은 S에 걸린 전압과 d1, d2, 그리고 ϕ에 따라 변한다. 그러므로 전자빔의 궤적을 컴퓨터 시뮬레이션하기 위해, E = 600, 800, 1,000, 1,200, 1,400eV, d1 = 0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0mm, d2 = 0, 5, 10, 15, 20, 25, 30, 35, 40mm, ϕ = 6.0, 6.4, 6.8, 7.2mm로 변화시키면서 표적에 도달하는 빔직경을 추적하였다.

그림 2는 SIMION 프로그램 상에서 전자빔의 궤적을 캡쳐한 것이다. 두 경우 모두 E = 1,000eV, ϕ=6.8mm로 동일하게 두고, d1=1.0mm일 때(그림 2(a))와 d1=2.0mm(그림 2(b)일 때 전자의 비행궤적을 컴퓨터 시뮬레이션한 결과이다. d1의 차이로 인하여 비행궤적이 확연히 차이가 남을 확인할 수 있다.

Fig. 2.

Capture of electron-trajectories on the SIMION program.

MCP에 도달하는 전자빔의 분포를 알기 위해서는 전자방출원(S)에서 180mm 떨어진 위치(그림 1(b))에서 측정해야 하지만, SIMION 프로그램상의 제약으로 180mm까지 비행궤적을 볼 수가 없었다. 그래서 전자방출원에서 표적까지 거리의 반(90mm)인 H 지점에 균일하게 도달하는 전자빔의 직경을 측정하고, 그 값의 2배를 MCP(180mm)에 도달하는 빔직경으로 간주하였다. 왜냐하면 전자방출원에서 출발한 전자는 표적까지 직선운동을 하기 때문에 그렇게 가정할 수 있다.

그림 2(a)에서 보는 바와 같이, 표적에 도달하는 전자빔의 분포가 균일한 부분이 있는 반면, 전자빔의 궤적이 표적을 크게 벗어난 전자도 있다. 그림 2(a)에서 전자빔의 궤적이 균일한 부분의 직경을 유효직경 D_H 라고 정의하고, 그 값의 두 배를 MCP에서의 유효직경 D라고 가정하여 D의 변화를 측정하였다.

그림 3은 그림 2(a)에서 전자방출원 부분을 확대한 것으로, 전자의 궤적와 등전위선을 함께 보여준 것이다. 전자방출원와 익스트랙터에 1,000V의 전압이 인가되어 있기 때문에 그림 3과 같은 등전위선을 형성하고, 이러한 전압구배 때문에 전자방출원에서 방출된 전자는 표적 쪽으로 가속이 된다.

Fig. 3.

Enlargement of the source part in Fig. 2(a)

그림 3에서 정의된(x,y) 좌표를 기준으로, 전자방출원(필라멘트)의 x축 좌표를 x=0으로 잡고, y축의 좌표를 변화시키면서 전자를 출발시켰다. 즉 전자가 출발하는 x축 좌표는 모두 0으로 잡고, y축 좌표는 y=-0.5mm에서 +0.5mm까지 Δy= 0.1mm의 간격으로 11개의 전자를 출발시킨 것이다.

표적으로 정의된 MCP의 직경은 20mm이고, MCP가 골고루 세척되기 위해서는 전자빔의 분포가 균일해야하기 때문에, 전자빔이 표적에 균일하게 도달하면서 직경이 20mm가 되는 조건을 찾고자 하였다.

Ⅲ. 컴퓨터 시뮬레이션 결과 및 고찰

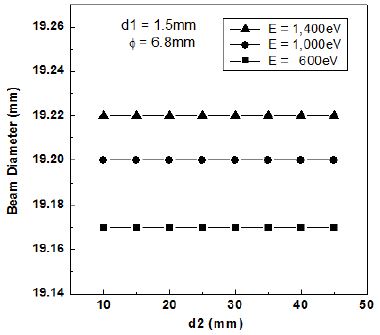
그림 4는 d1=1.5mm, ϕ=6.8mm로 고정하고, d2를 10~45mm까지 변화시키면서 빔직경을 컴퓨터 시뮬레이션한 결과이다. d2가 변함에 따라서는 빔직경이 거의 변하지 않음을 확인할 수 있다. 입사전자의 에너지를 각각 600, 1,000, 1,400eV로 바꾸면서 측정한 결과에서도 빔직경이 다소 변하기는 하지만 빔 직경은 19.15 ~ 19.22mm 정도로서 큰 차이가 없음을 알 수 있다.

Fig. 4.

d2-dependance of beam diameter

그림 5는 d1=1.5mm, d2=36mm로 고정하고 전자의 에너지 E와 익스트랙터 관의 직경 ϕ를 변화시키면서 빔직경을 컴퓨터 시뮬레이션한 결과이다. 빔직경은 전자의 에너지에 무관함을 확인할 수 있다. 그러나 익스트랙터 관의 직경이 변하면 빔 직경이 다소 크게 변함을 알 수 있다.

Fig. 5.

Energy-dependance of beam diameter

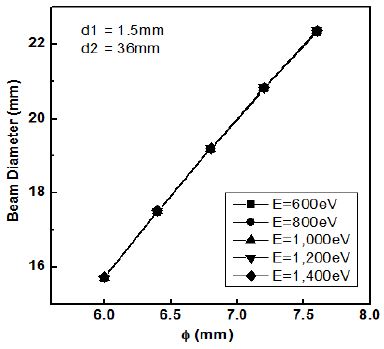
익스트랙터 관의 직경과 빔직경과의 관계를 확인하기 위하여, 그림 5의 데이터를 익스트랙터 관의 직경 ϕ의 변화에 따라 다시 그린 것이 그림 6이다. 그림 6에서 빔직경은 전자의 에너지와는 무관함을 다시 한번 확인할 수 있고, 익스트랙터 관의 직경에 따라서는 거의 선형적으로 변함을 알 수 있다. 즉 관직경이 6.0mm에서 7.5mm까지 변하는 동안 빔직경은 약 16mm에서 22mm까지 변함을 볼 수 있고, 이 결과로부터 20mm 내외의 빔직경을 얻기 위해서는 관직경이 6.8~7.2mm정도가 되어야 함을 알 수 있다.

Fig. 6.

ϕ-dependance of beam diameter

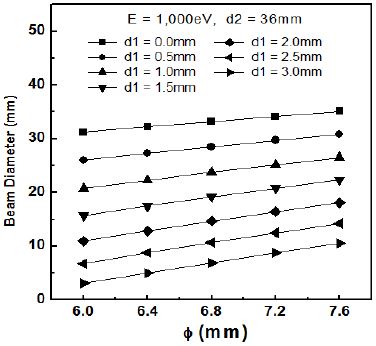
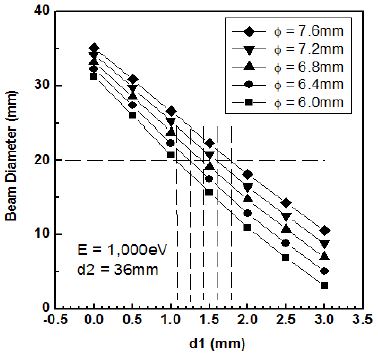
그림 7은 E = 1.000eV, d2 = 36mm로 고정하고, d1과 익스트랙터 직경 ϕ의 변화에 따른 빔 직경의 변화를 컴퓨터 시뮬레이션한 결과이다. d1이 고정되어 있을 때 ϕ의 변화에 따른 빔직경의 변화는 대략 0.6mm 내외로서 그리 크지 않다. 반면에 d1에 따라서는 빔직경이 매우 큰 차이를 보이고 있음을 알 수 있다. 이 변화를 명확히 확인하기 위하여 다시 그린 것이 그림 8이다.

Fig. 7.

ϕ-dependance of beam diameter

Fig. 8.

d1-dependance of beam diameter

그림 8에서 보는 바와 같이, d1이 0 ~ 3.0mm 변하는 동안 빔직경은 약 5 ~ 35mm까지 매우 크게 변함을 알 수 있고, ϕ에 따라서도 다소 변하고 있음을 확인할 수 있다. 그림 8에서 빔직경이 20mm가 되기 위한 d1값과 ϕ값을 확인해보면, d1이 증가함에 따라 ϕ도 같이 증가함을 알 수 있다.

d1과 ϕ가 서로 어떤 관계가 있는지를 확인하기위하여, 그림 8에서 빔직경이 20mm가 되기 위한 d1값과 ϕ값을 찾아서 보인 것이 그림 9이다. 그림 9에서 사각형 심볼은 그림 8에서 찾은 d1과 ϕ이고, 실선은 이 데이터를 이용하여 2차 함수로 피팅(Fitting)한 결과이다. 사각형 심볼과 피팅한 결과가 주 잘 일치함을 알 수 있다. 2차 함수로 피팅한 한 결과는 다음과 같다.

Fig. 9.

Relationship between ϕ and d1 values for beam dimeter to be 20mm

여기서 A = 0.0402, B = - 0.1039, C = 0.2580이다. 이 함수를 이용하여 빔직경이 20mm가 되기 위한 ϕ값과 d1값을 다시 계산한 결과를 정리한 것이 표 1이다. 이 결과를 이용하면 전자총을 설계할 때 익스트랙터 관의 직경이 결정되면 그에 적합한 d1값을 알 수 있다.

이상의 결과를 종합하면, 위의 네 가지 변수 E, d1, d2, ϕ중에서 전자의 에너지 E와 전자방출원과 관의 간격 d2는 빔직경에 거의 영향을 미치지 않음을 확인할 수 있었다. 반면에 익스트랙터 관의 직경 ϕ와 전자방출원과 익스트랙터 관의 간격 d1은 빔 직경에 크게 영향을 미침을 알 수 있었다. d1과 ϕ는 상호 2차함수적인 관계가 있고, 표적에서 20mm의 빔직경을 얻기 위해서는 표 1에 보인 d1과 ϕ값을 기준으로 설계하면 될 것으로 보인다.

Table 1.

ϕ and d1 values for beam dimeter to be 20mm

Ⅳ. 결 론

MCP 세척용 전자총을 개발하기 위하여, SIMION 프로그램을 이용하여 컴퓨터 시뮬레이션하였다. 표적인 MCP는 전자총의 전자방출원으로부터 180cm 위치에 있고 MCP의 직경은 약 20mm이기 때문에, MCP에 도달하는 전자빔의 직경이 20mm가 되는 조건을 찾았다.

컴퓨터 시뮬레이션 상에서 고려한 네 가지 변수 E, d1, d2, ϕ중에서, d2는 10mm에서 45mm까지 변화시키면서 빔직경의 변화를 관찰하였지만 빔직경에 거의 영향을 주지 않았다. d2는 전자총을 부착하는 1.33“CF 플랜지와 관련이 있기 때문에 짧게 하는 것은 한계가 있고, 설계상 가능한 범위(대략 30~50mm) 내에서 적절한 값을 선택하면 될 것으로 보인다.

d1, d2, ϕ가 고정되어 있을 때, 전자의 에너지 E를 500~1,500eV까지 변화시켜도 빔직경의 변화는 없었다. 따라서 MCP의 세척에 필요한 전자의 에너지가 1000eV근처이기 때문에, 전자총 설계시 에너지는 고려하지 않아도 될 것으로 생각된다.

표적에서 빔직경이 20mm가 되기 위한 d1과 ϕ값은 서로 2차함수적인 관계가 있음을 확인하였고, 피팅한 함수를 이용하여 계산한 d1과 ϕ값은 표 1과 같다. 익스트랙터는 1.33“CF 플랜지속에 들어가야 하고 절연을 해야 하는 문제가 있기 때문에, 전자총을 설계할 때 익스트랙터 관의 직경을 결정하는 데는 제한이 있다. 따라서 구조적으로 허용하는 범위 내에서 먼저 ϕ를 결정한 후, 표 1을 이용하여 d1값을 결정하면 된다. 즉, 구조적인 문제로 ϕ=7.0mm으로 해야 한다면, 표 1로부터 d1을 1.50mm로 결정하면 MCP에서 20mm의 빔직경을 얻을 수 있다는 의미이다.

이상의 결과를 바탕으로 현재 MCP 세척용 전자총의 설계 및 제작을 진행하고 있고, 제작된 전자총의 특성을 조사하여 시뮬레이션 결과와 비교 분석하여 MCP 세척에 적합한 전자총을 개발할 예정이다.

Acknowledgments

이 논문은 2017년도 목원대학교 연구년 지원에 의하여 연구되었음.

References

• Satish Dhawan, "Introduction to Microchannel Plate Photomultipliers", IEEE transactions on nuclear science, 28(1), p672-676, Oct), (1981. [https://doi.org/10.1109/tns.1981.4331261]
• Dominic J. Ruggieri, "Microchannel Plate Imaging Detectors", IEEE transactions on nuclear science, 19(3), p74-84, Oct), (1972. [https://doi.org/10.1109/tns.1972.4326705]
• W. Ho, and J. Richter, "Position‐sensitive detector performance and relevance to time‐resolved electron energy loss spectroscopy", Review of Scientific Instruments, 57(8), p1469-1482, (1986). [https://doi.org/10.1063/1.1138572]
• D. Dahl, "SIMION for the personal computer in reflection", International Journal of Mass Spectrometry, 200(1-3), p1-3, Dec), (2000. [https://doi.org/10.1016/s1387-3806(00)00305-5]
• D. C. McGilvery, "Photodissociation of positive ions – Thesis (Ph.D.)", La Trobe University, (1978).
• https://simion.com, . [accessed: Oct. 10. 2018]
• S. S. kim, "Mass Selection using Reflectron in the Gas Cluster experiment", J. of Kor. Vac. Soc, 12(2), p105-111, Jun), (2003.
• S. S. Kim, Y. S. Lee, D. Y. Kim, and D. S. Ko, "Computer Simulation for Development of Micro-Focus X-ray Generator", J. of Kor. Vac. Soc, 20(6), p403-408, Nov), (2011. [https://doi.org/10.5757/jkvs.2011.20.6.403]