전기 임피던스 단층촬영법에서 다층 신경회로망을 이용한 표적의 위치와 크기 추정

Ⅰ. 서 론

전기 임피던스 단층촬영법(EIT, Electrical Impedance Tomography)은 팬텀(Phantom)의 외부에 부착된 전극에 적절하게 설계된 전류를 흘려주는 동시에 전압을 측정하고 이들 데이터로부터 복원 알고리즘을 사용하여 내부 저항률(Resistivity) 분포를 얻는 기술이다. EIT는 다른 단층촬영법에 비하여 하드웨어 비용이 저렴하고 순간 해상도가 뛰어나며 비파괴적인 방법으로 팬텀 내부의 임피던스 분포에 대한 정보를 얻을 수 있는 등의 장점 때문에 재료공학, 지질학, 화공학 및 의공학 분야에서 모니터링 도구로 관심을 받고 있다.

EIT 시스템은 크게 하드웨어부과 영상복원부의 두 부분으로 나눌 수 있다. 하드웨어부에서는 적절하게 설계된 전류를 생성하여 팬텀의 외부에 있는 전극을 통해 인가시키는 동시에 각 전극에 유기되는 전압을 측정하며, 영상복원부에서는 인가한 전류와 측정된 전압데이터로부터 복원 알고리즘을 이용하여 내부의 저항률 분포를 추정한다. 일반적으로 EIT에서 영상복원은 비선형성(Non-linearity)과 부정치성(Ill-posedness) 등으로 인해 상당히 어려운 역문제(Inverse Problem)를 포함한다. 이로 인해, 다양한 복원방법을 시도함에도 불구하고 여전히 CT(Computed Tomography) 등의 다른 단층촬영법에 비해 복원된 영상의 공간 해상도가 낮고 표적의 경계를 정확히 찾기 어렵다[1]-[3].

신경회로망(Neural Network)은 패턴인식, 신호처리 및 영상처리, 패턴분류 문제 및 고장진단분야 등에 성공적으로 적용되고 있을 뿐만 아니라 비선형성이 강한 많은 공정 분야에 적용되어 좋은 성과를 보여 왔다[4]-[7]. 신경회로망의 장점으로는 복잡한 비선형 입출력 관계의 학습능력, 순차적 학습과정의 사용 및 데이터에 대한 적응능력을 들 수 있다. 신경회로망의 일부 보편적인 모듈은 연상 메모리와 학습능력을 보였다[8]-[10]. 또한, 신경회로망은 다양한 입력 및 출력 관계를 효율적으로 모델링 할 수 있으며, 병렬처리가 가능하므로 처리속도 측면에서 이점이 있다[11][12]. EIT에도 1990년대부터 신경회로망을 도입하여 지금까지 연구가 진행되고 있다[13].

일반적으로 EIT에서는 전극에서 측정한 전압으로부터 복원 알고리즘을 이용하여 팬텀 내부의 저항률 분포를 찾는다. 이와는 달리 경계추정 문제는 배경과 표적의 저항률은 미리 알고 있고 표적의 경계도 복잡하지 않고 완만하다고 가정한 상태에서 표적의 경계를 찾는다. 경계 추정문제를 다루는 대부분의 논문들은 푸리에 시리즈로 표적의 경계를 표현하고 역문제는 푸리에 계수를 찾는 것이다[14]. 표적의 경계가 원형 혹은 타원형일 경우에는 낮은 푸리에 차수로도 충분히 경계가 표현되지만 복잡한 모양의 표적일 경우에는 표현이 어렵고 차수도 높아져서 적용에 어려움이 있다.

이 논문은 다층 신경회로망(Multi-layer Neural Network)을 이용하여 원형인 표적의 위치(중심좌표)와 크기(반지름)를 추정하는 방법을 제안한다. 제안하는 방법에서는 표적을 원으로 가정하여 중심좌표와 반지름으로 표현하고 그때 측정된 전압을 이용하여 다층 신경회로망을 통해 학습시킨다. 이 방법에서는 배경과 표적의 저항률을 알고 있다고 가정하고 표적의 위치와 크기를 찾는 것에만 관심을 가진다. 제안한 방법의 추정성능을 확인하기 위해, 신경회로망을 학습시키고 다양한 컴퓨터 모의실험을 수행하였으며 추정 결과를 통해 제안한 방법의 성능을 확인하였다.

Ⅱ. 전기 임피던스 단층촬영법

일반적으로 EIT 문제는 정문제(Forward Problem)와 역문제로 구분되며, 정문제는 내부의 저항률 분포와 전극들을 통해 주입하는 전류를 알고 있는 경우에 전극에 유기되는 전압을 계산하는 과정이다. 이는 맥스웰 방정식(Maxwell's Equations)으로부터 유도되는 노이만(Neumann) 형의 경계조건을 갖는 라플라스(Laplace) 방정식으로 기술되며 지배방정식은 다음과 같다[15].

여기서 Ω와 ∂Ω는 각각 팬텀의 내부 영역과 경계면을 나타내고, ρ는 저항률 분포, u는 전기 포텐셜(Potential), e_l은 l번째 전극, z_l은 l번째 전극과 표면사이의 접촉저항, I_l과 U_l은 각각 l번째 전극을 통해 주입된 전류와 측정된 전압, v는 단위 법선벡터, L은 전극의 수이다.

EIT의 목적은 팬텀 외부에서 전기신호의 입ㆍ출력 관계를 통해 내부의 저항률 분포를 영상화 하는 것이다. 이를 위하여, 경계면의 전극을 통해 적절하게 설계된 전류를 인가한다. 전류의 인가방법은 인접, 대면, 기준 및 삼각함수 방법 등이 있으며 이 논문에서는 인접방법을 사용한다.

인접방법은 이웃하는 두 전극을 통해 전류를 주입하고 전류를 주입하지 않는 다른 모든 이웃하는 전극사이의 차이전압 데이터를 측정한다. L전극 시스템에서 입력 전류패턴의 수는 L이고 각 패턴에 대하여 (L-3)개의 차이전압 데이터가 측정되므로 측정되는 전압데이터의 수는 L×(L-3)이다. 이 방법은 주입 전류의 대부분이 팬텀의 경계 근처를 통하여 흐르므로 경계면 근처에서의 저항률 변화에 민감한 특징을 가진다. 그리고 이 방법은 측정 잡음이 존재할 때, 다른 전류패턴에 비해 평균자승복원오차(Mean Squared Reconstruction Error)가 작은 장점이 있다[16]. 따라서 인접방법은 측정오차에 민감한 EIT 문제에 적합한 전류패턴이라 할 수 있다.

Ⅲ. 다층 신경회로망을 이용한 표적의 위치와 크기 추정

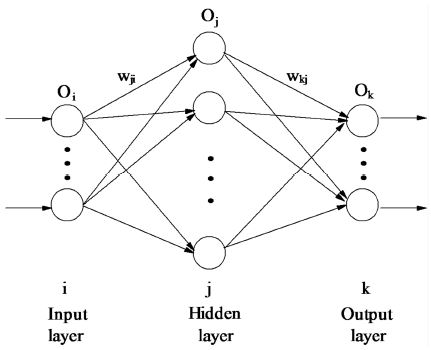
이 논문에서는 다층 신경회로망을 이용하여 전기 임피던스 단층촬영법에서 원형인 표적의 중심좌표와 크기를 추정하는 방법을 제안한다. 이용한 다층 신경회로망의 구조는 그림 1과 같이 입력층, 은닉층과 출력층으로 이루어져 있으며 각 층은 다수의 뉴런(노드)과 각 뉴런을 연결하는 가중치로 구성된다.

Fig. 1.

Architecture of the multi-layer neural network

그림 1의 다층 신경회로망으로부터 원하는 입출력 특성을 얻기 위해서는 신경회로망의 학습을 행하여야 한다. 본 논문에서는 다층 신경회로망의 학습을 위해서 SCG(Scaled Conjugate Gradient) 알고리즘[17]을 이용하여 가중치를 변화시킴으로써 이루어지며, 신경회로망을 학습시키기 위한 성능함수는 다음과 같이 정의한다.

여기서 n은 출력노드의 수이며, d_k(t)와 O_k(t)는 각각 k번째 출력노드의 목표값과 실제 신경회로망의 k번째 출력노드에서의 출력값이다.

SCG 학습 알고리즘은 Levenberg-Marquardt 방법과 Conjugate Gradient 방법을 결합하여 개선한 지도학습방법(Supervised Learning Method)이다. 학습할 때 직선탐색법(Line Search Method)을 수행하지 않으므로 반복속도(Iteration Speed)가 빠르며, 학습량이 많이 요구되는 문제에 적용할 때 매우 효과적이다. SCG 학습알고리즘은 다음과 같다[18][19].

• 1. 가중치벡터 $$ {\tilde{w}}_1$$ 와 스칼라 0<σ≤ 10^-4,
  0<λ₁≤10^-6, λ₁=0 선택.
  $$ {\tilde{p}}_1={\tilde{r}}_1=-E\text{'}\left({\tilde{w}}_1\right), t=1, success=true$$.

• 2. If success=ture, then 2차 정보계산:
  $$ {\sigma }_t=\sigma /\left|{\tilde{p}}_t\right|,$$
  $$ {\tilde{s}}_t=\left(E\text{'}\left({\tilde{w}}_t+{\sigma }_t{\tilde{p}}_t\right)-E\text{'}\left({\tilde{w}}_t\right)\right)/{\sigma }_t,$$
  $$ {\delta }_t={\tilde{p}}_t^T{\tilde{s}}_t.$$

• 3. 스케일 $$ {\delta }_t:{\delta }_t={\delta }_t+\left({\lambda }_t-{\overline{\lambda }}_t\right){\left|\widetilde{p_t}\right|}^2.$$

• 4. If δ_t ≤ 0, then 헤시안 양정부호행렬 생성 :
  $$ {\overline{\lambda }}_t=2\left({\lambda }_t-{\delta }_t/{\left|\widetilde{p_t}\right|}^2\right),$$
  $$ {\delta }_t=-{\sigma }_t+{\lambda }_t{\left|\widetilde{p_t}\right|}^2,$$
  $$ {\lambda }_t={\overline{\lambda }}_t.$$

• 5. 스텝사이즈 계산 :
  $$ {\mu }_t={\tilde{p}}_t^T{\tilde{r}}_t,$$
  $$ {\alpha }_t={\mu }_t/{\delta }_t.$$

• 6. 파라미터 비교 :
  $$ {∆}_t=2{\delta }_t\left[E\left({\tilde{w}}_t\right)-E\left({\tilde{w}}_t+{\alpha }_t{\tilde{p}}_t\right)\right]/{\mu }_t^2.$$

• 7. If Δ_k ≥ 0, then 성공적인 오차감소수행:
  $$ {\tilde{w}}_{t+1}={\tilde{w}}_t+{\alpha }_t{\tilde{p}}_t,$$
  $$ {\tilde{r}}_{t+1}=+E\text{'}\left({\tilde{w}}_{t+1}\right),$$
  $$ {\overline{\lambda }}_t=0, success=true.$$
  If t mod N = 0, then 알고리즘 재시작:
  $$ {\tilde{p}}_{t+1}={\tilde{r}}_{t+1}$$
   else:
  $$ {\beta }_t=\left({\left|{\tilde{r}}_{t+1}\right|}^2-{\tilde{r}}_{t+1}^T{\tilde{r}}_t\right)/{\mu }_t,$$
  $$ {\tilde{p}}_{t+1}={\tilde{r}}_{t+1}+{\beta }_t{\tilde{p}}_t.$$
  If Δ_t ≥ 0.75, then 스케일 파라미터 감소:
  $$ {\lambda }_t=\frac{1}{4}{\lambda }_t,$$
   else:
  $$ {\overline{\lambda }}_t={\lambda }_t, success=false.$$

• 8. If Δ_t < 0.25, then 스케일 파라미터 증가:
  $$ {\lambda }_t={\lambda }_t+\left({\delta }_t\left(1-{\mathrm{\Delta }}_t\right){\left|\widetilde{p_t}\right|}^2\right).$$

• 9. If 최대경사방향 $$ {\tilde{r}}_t\ne \tilde{0}$$ then t=t+1 and go to 2
  else 종료 후 $$ {\stackrel{-}{w}}_{t+1}$$을 원하는 최솟값으로 반환.

Ⅳ. 모의실험

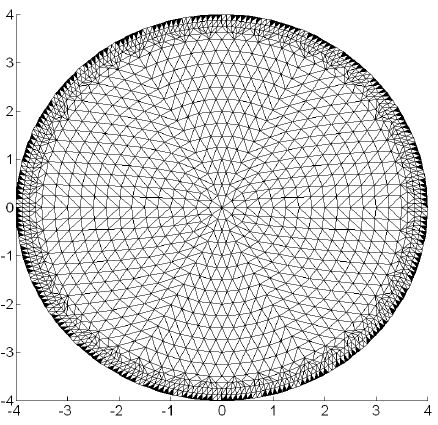
제안한 신경회로망 기반 알고리즘의 성능을 확인하기 위하여 컴퓨터 모의실험을 수행하였다. 모의실험을 위하여 그림 2와 같은 32개의 전극을 가지는 반지름이 4㎝인 원형의 팬텀을 고려하여 3104개의 요소와 1681개의 노드를 갖는 유한요소법(Finite Elements Method) 메시를 사용한다. 그리고 배경(Air)과 표적(Water)의 저항률은 각각 300Ωm과 600Ωm로 가정한다. 모의실험은 Intel(R) Core(TM) i7-3770 CPU와 8G RAM의 사양에서 수행되었고, 사용 프로그램은 MATLAB 2018b를 사용하였다.

Fig. 2.

Used mesh for simulations ([cm])

신경회로망의 입력은 전극에서 측정된 전압 데이터 U∈R^N×1이고 출력은 표적의 중심좌표 (x,y)와 반지름 r이다. 여기서 N은 전극의 수 L과 전류주입방법에 따라 결정되는데, 32개의 전극과 인접전류주입방법을 사용하면 N=L×(L-3)=928이 된다. 팬텀 내부에 반지름이 0.4㎝, 0.6㎝, 0.8㎝ 및 1.0㎝인 원형의 표적에 대하여 같은 위치에 표적의 중심좌표를 가지는 경우(각각 113개씩)에 대하여 전압을 측정하여 신경회로망의 학습에 사용하였다. 모의실험에서 사용하는 다층 신경회로망은 입력층, 1개의 히든층과 출력층으로 이루어져 있으며, 입력노드는 928개, 은닉노드는 32개이고 출력노드 3개이다. 학습을 위한 데이터 쌍은 113×4=452개이고 학습오차는 0.001로 하였다. 학습결과로는 학습반복횟수는 12372번, 학습시간은 122초가 걸렸다.

다층 신경회로망으로 학습된 결과에 대하여 표적의 추정성능을 확인하기 위하여 학습에 사용하지 않은 세 가지 표적에 대한 전압데이터(Data 1~3)를 이용하여 표적의 중심좌표와 크기를 추정하였다.

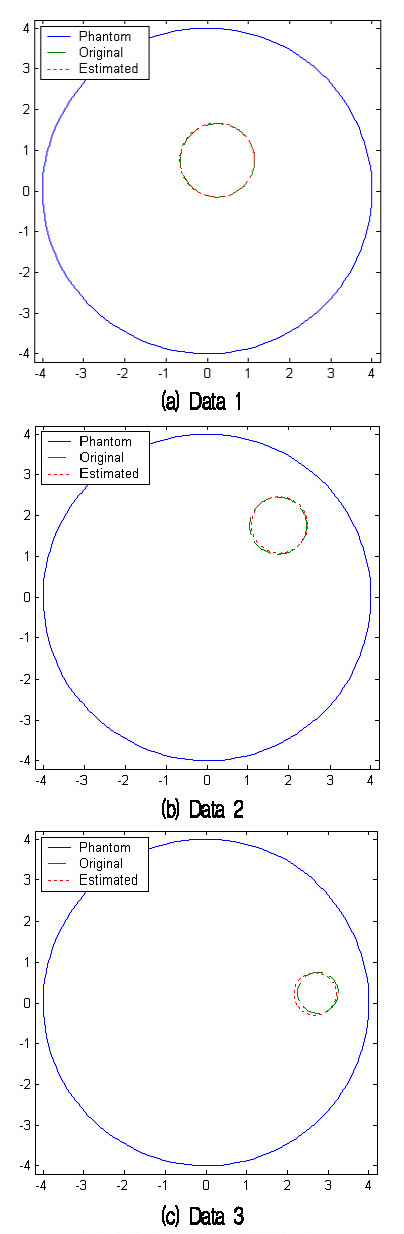
먼저 정성적인 평가를 위해, 그림 3에 Data 1~3의 원래 표적과 추정된 표적의 위치와 크기를 팬텀에 나타내었다. 그림 3으로부터 추정된 표적은 원래 표적의 위치와 크기를 잘 추정하는 것을 확인할 수 있다. 그림 3의 결과로부터 알 수 있는 사실은 표적의 크기가 클수록, 팬텀의 가운데에 있을수록 더 정확히 추정할 수 있다는 것이다.

Fig. 3.

Simulation results ([cm])

표 1은 세 가지 전압데이터로부터 추정한 표적의 중심좌표와 크기 및 오차(참값－추정값)이다. 표 1에서, 추정된 값들은 그림 3에서 확인한 것과 같이 참값에 대하여 0.01-0.07의 오차를 가지고 있으나 전체적으로 양호한 추정성능을 확인 할 수 있다. 표 1에서 오차의 크기를 살펴보면, 그림 3에서 확인한 것과 마찬가지로 팬텀의 경계부분에서보다는 중앙부분에서 오차가 작은 것을 알 수 있다. 이는 팬텀의 경계부분에서는 학습 데이터의 수가 상대적으로 적고 불연속적이지만, 가운데 부분에서는 학습 데이터의 수가 상대적으로 많고 일정하여 더 좋은 학습결과를 얻을 수 있기 때문이다.

Table 1.

Simulation results – estimated values and errors

마지막으로 정량적인 평가를 위해서 평균 제곱근 오차(RMSE, Root Mean Square Error)를 다음과 같이 정의하였다.

여기서 V는 원래 표적에 대한 전압데이터, $$ \widehat{V}$$는 추적된 표적에 대한 전압데이터이고 M은 전압데이터의 수이다. 비교를 위하여, EIT의 대표적인 알고리즘인 GN(Gauss-Newton) 방법을 사용하였다[20].

표 2는 GN 방법과 제안한 방법에 의해 얻어진 RMSE를 나타낸 것으로서 모든 경우에 대해 제안한 방법이 GN 방법보다 더 작은 값을 가짐을 알 수 있다. 그러므로 제안한 방법은 EIT에서 널리 사용되는 알고리즘인 GN보다 RMSE 관점에서 우수한 성능을 나타냄을 확인 할 수 있다.

Table 2.

Root mean square error

Ⅴ. 결 론

일반적으로 EIT에서 영상복원은 비선형성과 부정치성 때문에 만족할만한 복원결과를 얻기 어렵다. 한편 신경회로망은 비선형 시스템의 입력과 출력 사이의 관계를 효율적으로 모델링 할 수 있다.

이 논문에서는 신경회로망을 이용하여 측정된 전압 데이터로부터 원형인 표적의 중심좌표와 크기를 추정하는 방법을 제안하였다. 제안한 방법은 표적의 경계를 원으로 가정하여 표적을 중심좌표와 반지름으로 표현하고 그때 측정된 전압과의 관계를 다층 신경회로망을 통해 학습시켰다. 제안한 방법의 성능을 확인하기 위해 컴퓨터 모의실험을 수행하였으며 복원 결과를 통해 제안한 방법이 측정된 전압으로부터 표적의 위치와 크기를 추정하는데 유용함을 확인하였다.

경계부분의 효율적인 학습을 위한 연구와 더 복잡한 모양의 표적에 대한 추정방법 연구 등이 추후 과제이다.

References

• D. S. Holder, "Electrical Impedance Tomography: Methods", History and Applications, London, U.K., Institute of Physics Publishing, (2005).
• J. G. Webster, "Electrical Impedance Tomography", Bristol, U.K., Adam Hilger, (1990).
• J. H. Kim, B. S. Kim, C. Y. Kim, K. Y. Kim, and I. S. Lee, "Dynamic Directional Algebraic Reconstruction Technique for Time-Varying Imaging in Electrical Impedance Tomography", J. KIIT, 13(10), p1-8, Oct), (2015. [https://doi.org/10.14801/jkiit.2015.13.10.1]
• J. Johnson, and P. Picton, "Concepts in artificial intelligence", Butterworth-Heinemann LTD, Ch(4), p95-96, (1995).
• M. J. Willis, G. A. Montague, C. D. Massimo, M. T. Tham, and A. J. Morris, "Artificial neural networks in process estimation and control", Automatica, 28(6), p1181-1187, Nov), (1992. [https://doi.org/10.1016/0005-1098(92)90059-o]
• S. Bhama, and H. Singh, "Single layer neural networks for linear system identification using gradient descent technique", IEEE Trans. Neural Networks, 4(5), p884-888, Sep), (1993. [https://doi.org/10.1109/72.248467]
• S. C Lim, and G. W. Jin, "Alternative tactile sensor for measuring rehabilitation study using to neural network", Journal of IIBC, 12(4), p23-29, Aug), (2012. [https://doi.org/10.7236/jiwit.2012.12.4.23]
• J. Schurmann, "Pattern classification : a unified view of statistical and neural approaches", John Wiley and Sons, New York, (1996).
• T. Kohonen, "Self-Organizing Maps", Springer, Berlin, (1997).
• L. Fausett, "Fundamentals of neural networks : architectures, algorithms, and applications", Prentice Hall, (1994).
• C. C. Yang, S. O. Prasher, R. Lacroix, S. Sreekanth, N. K. Patni, and L. Masse, "Artificial neural network model for subsurface-drained farmlands", J. Irrig. Drain Eng, 123(4), p285-292, Jul), (1997. [https://doi.org/10.1061/(asce)0733-9437(1997)123:4(285)]
• C. C. Yang, S. O. Prasher, and G. R. Mehuys, "An artificial neural network to estimate soil temperature", Can. J. Soil Sci, 77(3), p421-429, Aug), (1997. [https://doi.org/10.4141/s96-062]
• A. Adler, and R. Guardo, "A neural network image reconstruction technique for electrical impedance tomography", IEEE Trans. Med. Imag, 13(4), p594-600, Dec), (1994. [https://doi.org/10.1109/42.363109]
• V. Kolehmainen, A. Voutilainen, and J. P. Kaipio, "Estimation of non-stationary region boundaries in EIT—state estimation approach", Inv. Prob, 17(6), p1937-1956, Nov), (2001. [https://doi.org/10.1088/0266-5611/17/6/324]
• E. Somersalo, M. Cheney, and D. Isaacson, "Existence and uniqueness for electrode models for electric current computed tomography", SIAM J. Appl. Math, 52(4), p1023-1040, Aug), (1992. [https://doi.org/10.1137/0152060]
• T. F. Schuessler, and J. H. Bates, "Current patterns and electrode types for single-source electrical impedance tomography of the thorax", Ann. Biomed. Eng, 26(2), p253-259, Mar), (1998. [https://doi.org/10.1114/1.116]
• D. E. Rumelhart, and J. L. McClelland, "Parallel distributed processing: explorations in the microstructure of cognition. Vol. 1: Foundations", MIT Press, Cambridge, MA, (1986).
• M. F. Moller, "A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning", Neural Netw, 6(4), p525-533, May), (1993.
• C. B. Khadse, M. A. Chaudhari, and V. B. Borghate, "Electromagnetic compatibility estimator using scaled conjugate gradient backpropagation based artificial neural network", IEEE Trans. Ind. Informat, 13(3), p1036-1045, Jun), (2017. [https://doi.org/10.1109/tii.2016.2605623]
• T. J. Yorkey, J. G. Webster, and W. J. Tompkins, "Comparing reconstruction algorithms for electrical impedance tomography", IEEE Trans. Biomed. Eng, BME-34(11), p843-852, Nov), (1987. [https://doi.org/10.1109/tbme.1987.326032]