다중 프로젝터를 이용한 초고해상도 3차원 형상 복원

Ⅰ. 서 론

객체의 사실적 표현을 위하여 정밀한 기하학적 형상을 측정하는 것은 필수적이다. 객체의 형상을 측정하기 위해서는 다양한 다른 시점의 영상을 획득해야 한다. 최근에는 형상과 반사 속성을 동시 측정할 수 있는 병렬 하드웨어 시스템이 제안되어 다수의 관점에서 영상을 획득 할 수 있다. 이러한 측정 방법들은 궁극적으로 정교한 객체의 3차원 영상을 다루기 위함이다[1]-[3].

먼저 구조광 시스템은 객체의 3차원 정보를 복원하기 위해 널리 사용되는 방법이다. 구조광 시스템은 다양한 패턴을 객체에 투사하는 프로젝터 시스템과 그 구조광이 투사된 객체의 영상을 순차적으로 획득하는 카메라 시스템으로 간단하게 구성된다. 그리고 획득한 영상을 복호화 함으로써 강건하게 카메라의 픽셀과 프로젝터의 픽셀 사이의 대응점을 설정하고, 이 대응점으로부터 삼각 측량법을 통해 최종적으로 기하 정보를 추정한다. 이러한 구조광 시스템은 다중 스테레오에서 어려움을 겪고 있는 텍스처리스(Textureless)형태의 객체에도 강건한 기하정보를 제공한다. 그러나 최근 수 년 동안 구조광 시스템의 구성에서 쟁점이 되는 것은 카메라 센서의 해상도와 프로젝터의 해상도 차이에서 발생하는 기하 정보 오차가 점점 커지고 있다는 것이다. 비용측면에서 수 십 메가 해상도의 영상센서는 쉽게 구할 수 있지만, 프로젝터 시스템은 물리적 기술의 한계와 시장성으로 인해 단지 수 메가 픽셀의 해상도에 그치고 있는 실정이다.

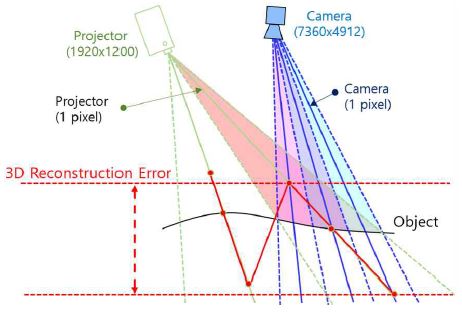
일반적인 구조광 시스템의 복호화 방식에 따라 추정하는 기하 정보의 정확도는 프로젝터 시스템의 해상도에 의존한다. 그림 1에서 보는 것과 같이 구조광 시스템은 영상 센서의 모든 픽셀로부터 프로젝터 전체 픽셀 좌표를 복호화 할 수 있으나 카메라와 프로젝터 해상도의 불균형에 따라 추정된 객체의 기하 정확도는 제한될 수 밖에 없다. 객체의 3차원 복원은 삼각 측량법을 이용하여 획득하게 되는데, 카메라와 프로젝터 픽셀의 중심을 기준으로 만나는 점을 계산하게 된다. 이때, 카메라와 프로젝터간의 해상도 불균형에 따라 그림 1과 같은 에러가 발생하게 되며, 결과적으로 톱니형상의 복원이 발생한다. 이와 같은 문제를 해결하기 위하여 최근 수 년간 프로젝터의 서브픽셀을 추정하는 다양한 방법들이 제시되었다. M. Ritz[4]은 기계 장치를 추가하여 프로젝터의 렌즈를 정밀하게 이동하는 동시에 구조광 패턴을 투사하여 객체의 영상을 획득한다. 이것은 렌즈 이동을 통해 프로젝터의 서브 픽셀의 추정이 가능함을 의미한다. 그러나 프로젝터의 렌즈를 정교하게 좌우 또는 상하로 이동시키는 기계적 시스템을 추가하는 것은 상당한 비용이 요구된다.

Fig. 1.

Shape reconstruction error due to camera and projector resolution difference

프로젝터의 서브 픽셀을 추정하는 또 다른 접근법으로 프로젝터의 각 픽셀에서 밝기 변화를 분석하여 객체에 임의로 이동하는 정현파 형태의 패턴을 투사하는 사인 곡선 투사 방법이 있다[5][6]. 이 방법은 프로젝터로 정확한 정현파의 패턴을 생성할 수 있다고 가정을 하고 있으나 프로젝터 광원 밝기로 정확한 정현파를 구현하는 것은 어려운 일이다. 그리고 프로젝터의 직선 형태의 구조광 패턴을 객체에 투영 한 후 획득한 영상에서 그 패턴을 분석하여 프로젝터의 서브 픽셀을 추정 할 수 있는 방법이 제안되었다[7]-[9]. 이러한 접근법은 프로젝터를 능동광원으로 간주하여 BRDF(Bidirectional Reflectance Distribution Function)모델링을 통해 프로젝터의 서브 픽셀을 추정하고 있지만, 궁극적으로 이 방법은 프로젝터 센서 측면이 아닌 카메라 센서 측면에서 서브 픽셀을 추정하는 것이며, 객체의 표면을 평면으로 가정하기 때문에 종종 부정확한 결과를 보이기도 한다.

본 논문에서는 프로젝터의 해상도 제한으로 기인한 구조광 시스템의 기하 정보 오차를 극복하기 위해 다중 카메라와 다중 프로젝터를 이용하여 초고해상도 방법을 통해 정밀한 기하 정보를 획득하는 방법을 제안한다. 이 방법은 다수의 다른 시스템의 프로젝터 패턴을 투사하고, 패턴이 중첩되면서 객체표면을 최소 영역(픽셀단위의 레이블)으로 고유하게 식별 할 수 있도록 한다. 따라서 밀도가 높은 정확한 3차원 점군을 획득 할 수 있다.

2장에서는 다중 프로젝터 기반의 구조광 시스템에서 순차적인 패턴 중첩을 통한 객체의 최소 영역을 구분하는 방법을 서술하며, 3장의 실험 결과에서는 2장의 내용을 토대로 금속 시편을 이용하여 기하 획득의 정밀도를 수치적으로 분석한다. 마지막으로 4장에서는 결론 및 앞으로의 연구 방향에 대하여 논한다.

Ⅱ. 다중 카메라-다중 프로젝터 기반의 구조광 시스템

실험에 사용된 다중 영상 획득 카메라는 7360×4912 해상도의 DSLR Nikon D810 두 대를 스테레오 기반으로 구성했으며 다수의 구조광 패턴 중첩을 위하여 1920×1200 해상도의 Epson EB1985 WUXGA 프로젝터 1대를 삼각대에 장착하여 프로젝터를 여러 다른 위치에 배치함으로써 다중 프로젝터와 동일한 설정을 유지했다. 연산 장치는 3.60GHz CPU Intel i7과 16GB 메모리를 사용하였다.

제안하는 다중 카메라-다중 프로젝터 구조광 시스템은 정적인 객체에 다수의 구조광 패턴을 중첩하고 순차적인 프로젝터의 구조광 패턴을 복호화함으로써 스테레오 또는 다수의 카메라에서 서로 대응 하는 픽셀을 검색한다. 그림 2에서 프로젝터 1, 2, 3의 순차적인 패턴 중첩을 통하여 객체 표면의 최소 영역은 스테레오 또는 다중 카메라에서 쉽게 식별이 가능하다.

이 방법은 높은 밀도와 정확도로 기하 정보를 획득할 수 있을 뿐만 아니라 구조광에 의해 생성되는 밀도 높은 패턴으로 텍스처리스 객체의 기하 정보를 복원하는 것에도 매우 효과적이다.

다수의 프로젝터를 P, 다수의 카메라는 C이면, 획득 한 전체 영상은 I = i_m,n|i_m,n∈P ×C이다.

식 (1)의 함수 f : R → Rⁿ는 c번째 카메라 좌표 x에서 순차적으로 다수 구조광 패턴의 복호화에 따른 프로젝터 좌표 y_n을 나타낸다.

식 (2)는 다중 프로젝터와 스테레오 카메라 환경으로 단순화하여, 두 카메라의 좌표 x_l, x_r는 함수 f를 통하여 순차적인 다수의 프로젝터 좌표 벡터 $$ \overrightarrow{p_{xl}}=\left(y_1\cdots y_n\right), \overrightarrow{p_{xr}}=\left(y_1\cdots y_n\right)$$의 변환을 보여 준다. 그리고 각각의 카메라에서 얻은 프로젝터 좌표 벡터 집합의 교집합을 통해 두 카메라의 대응점을 구할 수 있다.

그림 2는 위 과정을 통해 정육면체의 금속 시편에 대한 프로젝터의 서브 픽셀을 추정한 결과이다.

Fig. 2.

Multi-camera-multi projector based structured light system

그림 2에서 단일 구조광(Single Structured Light)은 단일 프로젝터와 카메라로 구성된 구조광 패턴 영상이며 프로젝터에서 하나의 픽셀이 투사되는 표면에 카메라에서 여러 픽셀로 보여진다. 그러나 다중 구조광(Multiple Structured Light)은 다중 프로젝터와 스테레오 카메라로 구성된 구조광 패턴 영상이며 중첩된 다수의 프로젝터 구조광은 표면을 카메라한 픽셀 영역과 같은 최소 영역으로 분할한다. 이것은 스테레오 기반의 형상 복원에서 카메라의 한 픽셀 단위로 기하 정보를 획득할 수 있음을 의미한다.

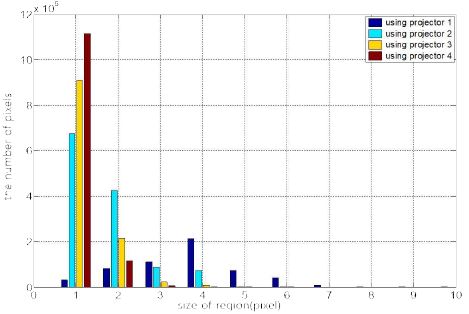
그림 3은 그림 2의 정육면체에서 얻어진 구조광 패턴의 레이블 크기의 분포 그래프이다. 그림 3 그래프의 x축은 프로젝터 픽셀 영역(레이블) 대비 카메라의 픽셀 영역의 크기를 의미하고, y축은 프로젝터 픽셀 영역 대비 카메라의 픽셀 수의 빈도이다. 프로젝터 1개를 사용하였을 경우 가장 많이 분포하는 프로젝터의 레이블 당 카메라 픽셀 수는 4개이다. 그러나 사용된 프로젝터의 수가 증가됨에 따라 가장 많이 분포 하는 레이블의 카메라 픽셀 수는 1개이다. 이는 다수의 프로젝터 구조광 패턴이 중첩되어 객체 표면을 거의 카메라 하나의 픽셀 단위로 분할 할 수 있음을 보여주는 것이며 프로젝터 4개를 사용했을 경우 중첩된 구조광 패턴의 전체 레이블은 95%이상으로 1픽셀로 분할된다. 이는 제한된 프로젝터의 해상도에 의해 발생하는 기하 오차를 최소화 하며 획득한 기하 형상에 대한 수평 해상도가 개선됨을 보여주는 것이다.

Fig. 3.

Distribution of label of projector coordinates by overlapping multiple structured light patterns

Ⅲ. 실험 결과

본 실험에서는 다중 카메라-다중 프로젝터 기반의 구조광 시스템을 적용하여 객체의 정밀한 기하정보를 획득한다. 제안한 확장 형태의 구조광 시스템의 기하 획득에 대한 정밀도 평가 방법으로 이미 기하 모델을 알고 있는 12×12×12cm의 정육면체 금속 시편을 이용하였으며, 평가 항목으로는 구조광 시스템으로부터 획득한 금속 시편의 기하 정보에 대하여 평탄도(Flateness)와 직각도(Squareness) 측정과 재투영 오차(Reprojection Error)를 이용한다.

단일 구조광 시스템과 다중 카메라-다중 프로젝터 기반의 구조광 시스템에 대하여 평가 항목을 비교함으로써 제안한 방법이 정교한 기하 정보 획득 측면에서 개선됨을 증명한다.

3.1 단일 구조광 시스템의 기하 정밀도 평가

그림 4는 정밀도 측정에 사용된 금속 시편의 영상과 단일 구조광 시스템에서 금속 시편의 기하 정보를 획득한 영상이다. 기하 보정이 완료된 스테레오 기반의 카메라를 이용하여 12×12×12cm의 정육면체 금속 시편을 단일 구조광 시스템을 이용하여 3차원 형상으로 복원하였다. 그리고 그림 5는 획득한 시편의 형상에 대하여 RANSAC(Random Sample Consensus)방법을 이용하여 평면 방정식 계수를 추정한다.

Fig. 4.

Reconstruction of metal specimens used to measure the geometrical reconstruction accuracy of single structured light systems

Fig. 5.

Metal specimen obtained through the single structured light system

일반적으로 RANSAC방법은 최소 자승법에 비해 상당수의 아웃라이어가 포함된 데이터에 대하여 강건한 모델 계수를 추정한다.

먼저 평탄도는 RANSAC방법을 통해 추정한 평면과 획득한 시편의 형상의 최소 유클리드거리로 측정한다. 재투영 오차는 시편의 기하 보정 패턴 영상에서 2차원 패턴 좌표를 추출하고 구조광 시스템을 통해 추출된 2차원 기하 보정 패턴 좌표에 대한 3차원 기하 정보를 획득한 후 다시 카메라 영상으로 투영함으로써 기하 정보 획득에 대한 픽셀 오차를 보여준다. 단일 구조광 시스템의 기하 정보 획득에 대한 평가는 표 1과 같다.

Table 1.

Evaluation of geometric reconstruction accuracy of single structured light system

그림 6은 구조광 시스템을 통해 획득한 시편의 형상(Red Plane)과 RANSAC을 통해 추정한 평면 사이의 유클리드 거리를 히스토그램으로 보여준다. 히스토그램의 구간 크기는 0.1mm이고 시편의 형상과 추정한 평면의 유클리드 거리의 평균값은 0.376mm이다.

Fig. 6.

Histogram of the red plane of the specimen and the distance of the estimated plane obtained from the single structured light system

그림 7은 시편 형상(Green Plane)과 RANSAC을 통해 추정한 평면 사이의 유클리드 거리를 히스토그램으로 보여준다. 시편의 형상과 추정한 평면의 유클리드 거리의 평균값은 0.381mm이다.

Fig. 7.

Histogram of the green plane of the specimen and the distance of the estimated plane obtained from the single structured light system

두 평면에 대한 직각도는 90.08도이며 재투영 오차는 1.38(rms)이다.

3.2 다중 카메라-다중 프로젝터 기반 구조광 시스템의 정밀도 평가

다중 카메라-다중 프로젝터 기반 구조광 시스템의 기하 획득의 정밀도 평가는 앞선 단일 구조광 시스템과 동일한 방법으로 수행하였다. 그림 8은 다중 카메라-다중 프로젝터 기반 구조광 시스템에서 동일한 금속 시편에 대한 구조광 패턴을 투사한 영상과 시편의 형상을 획득한 영상이다. 또한, 단일 구조광 시스템의 평가 방법은 RANSAC방법을 이용하여 평면의 방정식 계수를 추정하고 각각 추정한 평면을 보여준다.

Fig. 8.

Shape of specimen obtained through multi-structured light system

표 2는 단일 구조광 시스템과 다중 카메라-다중 프로젝터 기반 구조광 시스템의 기하 획득의 정밀도를 비교하여 보여준다. 두 평면에 대한 평탄도에 대한 평균 거리와 재투영 오차는 단일 구조광 시스템에 비해 약 2배 정도 개선되었으며, 직각도는 거의 차이가 없다.

Table 2.

Evaluation of geometric reconstruction accuracy of single and multi structured light

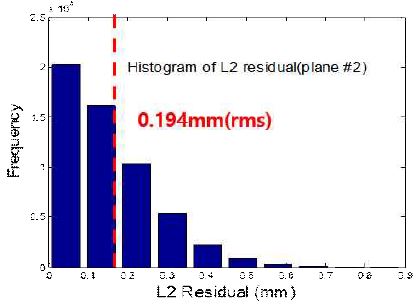
그림 9와 10은 앞선 평가 과정과 같이 다중 카메라-다중 프로젝터 기반 구조광 시스템에서 획득한 시편의 형상(Red, Green plane)과 RANSAC을 통해 추정한 평면의 유클리드 거리를 히스토그램으로 보여준다. 두 그림 모두 추정한 평면과 시편 형상 사이의 거리는 95% 이상이 0.4mm 이내에 있음을 보여준다.

Fig. 9.

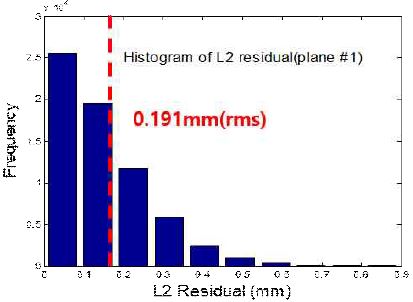
Histogram of the red plane of the specimen and the distance of the estimated plane obtained in the multi-structured light system

Fig. 10.

Histogram of the green plane of the specimen and the distance of the estimated plane obtained in the multi-structured light system

3.3 구조광 기반의 3차원 모델 생성

구조광으로 사용된 영상 패턴은 11단계(211 = 2048)의 그레이코드(Gray code)이다. 카메라의 기하보정은 2개의 영상 획득용 카메라와 1개의 패턴 투사용 프로젝터를 이용하여 각각의 카메라에 대한 기하 보정을 수행하였다. 구조광 시스템의 기하 보정이 완료된 후에는 3차원 형상을 획득하고자 하는 객체를 회전 테이블에 고정한다.

그리고 임의로 회전된 회전 테이블 위의 객체에 구조광 패턴을 투사함으로써 패턴이 투사된 객체 영상을 획득하고 복호화를 통해 카메라와 프로젝터의 대응점을 계산한다. 앞서 계산된 카메라의 기하보정과 복호화를 통해 얻은 대응점을 입력으로 삼각 측량법을 통해 최종적인 객체의 3차원 점군을 획득한다.

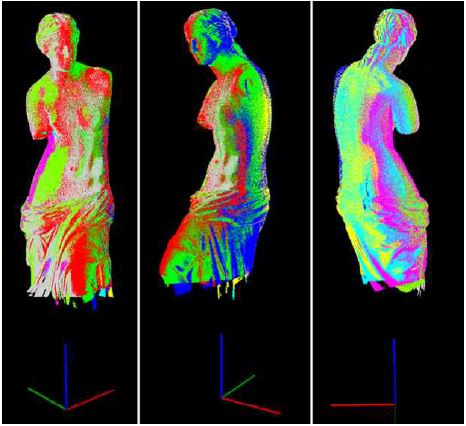
실험에서는 그림 11과 같이 45º간격으로 8번 회전 테이블의 회전으로 다른 시점에서 객체의 3차원 점군을 획득한다. 그림 12은 서로 인접하는 시점의 점군에 대하여 ICP(Iterative Closest Point) 방법[10]으로 정합을 수행한 결과이다. 그리고 모든 점군에 대하여 정합을 수행한 결과는 그림 12에서 보여준다. 그림 12에서의 색상은 각기 다른 시점에서 획득한 점군을 뜻한다. Besl에서 제시한 ICP 알고리즘은 실외 환경에서 획득한 3차원 점군뿐만 아니라 본 실험에서 획득한 구조광 시스템 기반의 대규모의 3차원 점군에서도 상당한 수준의 정합 결과를 보인다. 그러나 고해상도 구조광 시스템을 통해 획득한 대규모 점군에 대한 정합의 계산 복잡도는 매우 높은 편이다.

Fig. 11.

Point cloud acquired at various points through rotation of turntable

Fig. 12.

Three-dimensional point cloud registration at 8 points through ICP method

그림 11, 12의 실험에서는 한 시점에 대략 100만개의 점군을 획득하였고, 전체 획득한 점군의 수는 약 800만(8시점)이다.

Ⅳ. 결론 및 추후 과제

본 논문에서는 높은 밀도와 정확한 3차원 모델을 획득하는 시스템과 방법을 제안했다. 제한된 프로젝터의 해상도에 의해 야기되는 기하 복원 오차를 극복하기 위해 다중 카메라-다중 프로젝터 기반의 초고해상도 기법을 활용하여 높은 밀도의 정확한 3차원 점군을 획득하였다. 본 실험에서는 하나의 프로젝터를 서로 다른 위치에 배치함으로써 객체 표면의 최소 영역을 고유하게 암호화할 수 있도록 구조광 패턴을 중첩하여 투영하였으며, 그 중첩된 구조광 패턴을 복호화 함으로써 밀도가 높은 정확한 3차원 형상을 복원하였다. 그리고 금속 시편을 이용하여 단일 구조광 시스템과 다중 카메라-다중 프로젝터 기반의 구조광 시스템의 기하 획득의 정밀도를 수치적으로 비교하였으며 제안한 방법으로 객체의 형상 복원 정밀도가 상당히 개선되었다. 또한 통계적 분석을 통하여 최적의 다중 프로젝터의 수를 예측하였다.

향후의 연구는 계산 복잡도가 높은 ICP 알고리즘의 최적화를 진행하여 전체적인 시스템의 향상을 목표로 할 것이며, 이 후 TSDF(Truncated Signed Distance Function)와 Marching Cube를 통한 점군을 메시(Mesh)로 만드는 것을 목표로 할 것이다.

Acknowledgments

이 논문은 2018년도 정부(과학기술정보통신부)의 재원으로 '범부처 Giga KOREA 사업'의 지원을 받아 수행된 연구임 (No.GK18P0300, 초실감 서비스를 위한 동적 객체의 실시간 4D 복원 기술 개발)

References

• G. Muller, G. H. Bendels, and R. Klein, "Rapid synchronous acquisition of geometry and BTF for cultural heritage artefacts", in VAST ‘05, 2005, p13-20, Nov), (2005.
• B. Wilburn, N. Joshi, V. Vaish, E. -V. Talvala, E. Antunez, A. Barth, A. Adams, M. Horowitz, and M. Levoy, "High performance imaging using large camera arrays", in SIGGRAPH 2005, p765-776, Aug), (2005. [https://doi.org/10.1145/1186822.1073259]
• K. Li, Q. Dai, and W. Xu, "Markerless shape and motion capture from video sequences", IEEE Transactions on Circuits and systems for video Technology, 21(3), p320-334, Mar), (2010.
• M. Ritz, M. Scholz, M. Goesele, and A. Stork, "High resolution acquisition of detailed surfaces with lens-shifted structured light", in VAST’10, p1-8, Feb), (2012. [https://doi.org/10.1016/j.cag.2011.10.004]
• D. Scharstein, and R. Szeliski, "High-accuracy stereo depth maps using structured light", In IEEE Conference on Computer Vision and Pattern Recognition, 1, p195-202, Jun), (2003.
• S. Zhang, and S. T. Yau, "Generic non-sinusoidal phase error correction for three-dimesional shape measurement using a digital video projector", Appl. Opt, 46(1), p36-43, Oct), (2007. [https://doi.org/10.1364/ao.46.000036]
• J. Guhring, "Dense 3-d surface acquisition by strctured light using off-the-shelf components", In Proc. Videometrics and Optical Methods for 3D Shape Measurenent, p220-231, Jan), (2001.
• C. J. Taylor, "Implementing high resolution structured light by exploiting projector blur", Workshop on Applications of Computer Vision WACV, IEEE, p9-16, Jan), (2012. [https://doi.org/10.1109/wacv.2012.6163001]
• Y. Park, and Y. Seo, "Enhancement Depth Map Computation", KCGS 2016, p187-188, Jul), (2016.
• P. J. Besl, and N. D. McKay, "A method for registration of a 3-D shapes", IEEE Trans Pattern Analysis and Machine Intelligence, 14(2), p239-256, Feb), (1992. [https://doi.org/10.1109/34.121791]