펄스 기반의 공간다중화 초광대역 시스템을 위한 Zero-Forcing 수신기들의 성능 비교 및 분석

Ⅰ. 서 론

초광대역(UWB, Ultra-WideBand) 기술은 수 GHz의 매우 넓은 주파수 범위에 걸치는 매우 좁은 펄스를 사용하여 많은 양의 데이터를 전송할 수 있는 근거리 무선통신이나 레이더 분야 등에서 활발하게 연구되어 왔다[1]-[3]. 한편 MIMO(Multiple Input Multiple Output) 기술은 무선통신 채널에서 빠른 데이터 속도와 높은 안정성을 제공할 수 있는 장점으로 다양한 측면에서 진화되고 발전되었다[4][5]. 이러한 MIMO는 실내 무선통신 환경에서 대용량의 고-신뢰성을 위해서 UWB 통신시스템에 접목될 수 있다[6].

실내 공간다중화 UWB-MIMO 시스템은 로그-정규 분포 다중경로 페이딩 채널을 경험하게 되어 기존의 단일 경로에서 사용되는 MIMO 수신기를 그대로 적용했을 때 기대하는 성능을 얻을 수가 없다[7]. 그래서 UWB-SISO(Single Input Single Output) 시스템에서 다중경로를 결합하기 위한 Rake 방식을 UWB-MIMO 시스템에서 활용한 수신기에 대한 연구가 이루어졌다[8]-[10]. 참고문헌 [8]에서는 로그-정규 분포 다중경로 채널에서 공간다중화 UWB MIMO 무선통신 시스템을 위한 ZF(Zero-Forcing) 필터 기반의 Rake 수신기의 오류 성능 분석이 이루어졌다. 다중경로 채널을 경유한 공간 다중화된 송신 데이터 스트림을 분리하기 위해 경로별로 ZF 필터링을 먼저 수행한 후 각각의 데이터 스트림별로 MRC(Rake Maximum Ratio Combining)을 수행한다. 본 논문에서 이러한 수신기 구조를 ZF-Rake라는 용어를 사용한다. ZF-Rake 수신기의 성능을 향상시키기 위한 연구로 참고문헌 [10]에서 각각의 경로 별로 Rake MRC를 먼저 수행하고 그 출력 신호에 대해 다중경로 Rake MRC를 수행한 후 ZF 필터링을 한번 진행하는 수신기 구조가 제안되었으며, 본 논문에서는 2Rake-ZF라고 부른다.

ZF-Rake 수신기와 2Rake-ZF 수신기들은 실제로 구현 시에 ZF 필터링과 경로 Rake MRC 부분이 구현이 되어 구현 복잡도가 높다는 단점이 있다. ZF 필터링 과정에서도 MRC 과정을 수행할 수 있기 때문에 수신기의 구조를 바꿔서 구현 시에 복잡도를 줄이기 위한 연구가 필요하다.

본 논문에서는 위에서 언급된 ZF-Rake와 2Rake-ZF 수신기 구조와는 다른 eZF(extended ZF) 수신기를 소개한다. 단일경로 채널에서 사용된 기존의 ZF MIMO 수신 기법을 다중경로 채널에서 확장된 채널 행렬과 수신 신호 벡터에 직접 적용함으로써 실제 구현 시 복잡도를 줄일 수 있다. 이러한 eZF 수신기의 구조가 제공할 수 있는 다양성 이득을 이론적으로 분석하고, 그와 동시에 이론적인 평균 BER(Bit Error Rate) 성능 분석 결과를 함께 제시한다. 또한 시뮬레이션을 통하여 eZF 수신기의 BER 성능을 ZF-Rake와 2Rake-ZF 수신기와 비교 평가하고, 이러한 세 가지 종류의 수신기 구조들에 대해 다양성 이득과 이론적인 BER 성능 측면에서도 결과들을 비교 분석한다.

Ⅱ. 시스템 모델

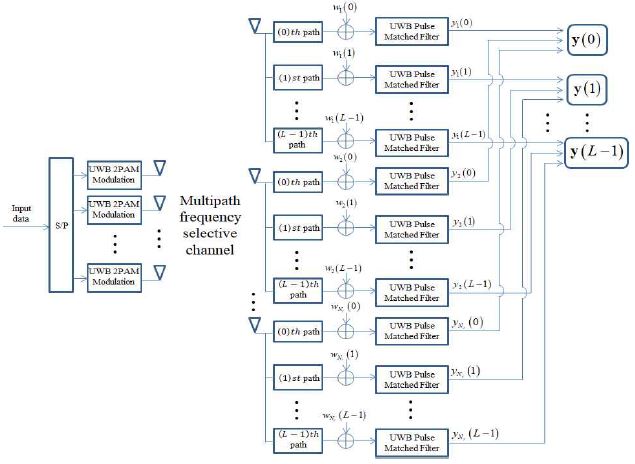
본 논문에서는 그림 1에서와 같이 N_t개의 송신 안테나와 N_r개의 수신안테나를 사용하는 펄스 기반의 공간다중화 초광대역 MIMO 시스템을 고려한다. 2진 펄스 진폭 변조(2PAM, binary Pulse Amplitude Modulation)된 송신 데이터 스트림이 N_t개의 서로 다른 송신안테나를 통하여 독립적으로 전송된다. 여기서, 심볼간 간섭을 피하기 위하여 펄스 반복 주기는 채널 지연 확산(Channel Delay Spread)에 비하여 충분히 크다고 가정한다. 각각의 송신안테나 출력신호는 주파수 선택적 다중경로 페이딩 채널을 통해 전송되고, L개의 다중경로 성분만을 수신기에서 이용한다고 가정한다. 수신안테나에서 UWB 펄스 정합 필터를 사용한 경우, 이산 시간 수신 신호 벡터는 다음과 같이 표현될 수 있다[8].

Fig. 1.

Spatial multiplexing UWB-MIMO system

여기서 E_b는 비트당 평균 에너지를 표시하고, N_r개의 수신안테나를 통해 수신되는 신호 열벡터는 y(l) = [y₁(l) y₂(l) ⋯ y_Nr(l)]^T로 주어지고, y_m(l)은 l번째 다중경로 성분이 m번째 수신안테나를 통하여 수신될 때의 수신신호를 나타낸다. 또한 N_t개의 송신안테나를 통해 독립적으로 전송되는 비트 데이터는 b = [b₁ b₂ ⋯ b_Nt]^T로 표현된다.

그리고 N_r개의 수신안테나의 l번째 다중경로에 해당하는 잡음 신호 열벡터는 w(l)=[w₁(l ) w₂(l ) ⋯ w_Nr(l)]^T로 주어진다. 여기서 w_m(l)는 m번째 수신안테나 잡음 신호로 평균이 0이고 분산 값이 N₀/2인 부가성 백색 가우시안 잡음(AWGN, Additive White Gaussian Noise)으로 가정한다.

l번째 다중경로 성분에 해당하는 N_r × N_t크기를 가진 이산 통신 채널 행렬 H(l)은 H(l) =[h₁(l) h₂(l) ⋯ h_Nt(l)]로 주어지며, 여기서 열벡터 h_n(l)은 h_n(l)= [h_1n (l) h_2n(l) ⋯ h_Nrn(l)]^T이고, h_mn(l)은 n번째 송신안테나로부터 m번째 수신안테나를 통하여 전달되는 l번째 경로에 해당하는 채널 이득 계수를 표시한다. 채널 이득은 h_mn(l)= α_mn(l)η_mn(l)로 주어지며, α_mn(l)∈{+1,-1}는 펄스 위상을 나타내는 이산 랜덤변수이고, η_mn(l)는 로그-정규 분포 특성을 가진 페이딩 진폭을 나타내고 η_mn(l) = e^θ_mn(l)로 주어진다. 여기서 θ_mn(l)은 평균 μ_θmn(l)와 분산 $$ {\sigma }_{\theta }^2$$을 가진 가우시안 분포 특성을 가진다. 분산 $$ {\sigma }_{\theta }^2$$값은 인덱스 l, m, n에 무관하다고 가정한다. 또한 η_mn(l)의 k번째 모멘트는 $$ E\left[{\eta }_{mn}{\left(l\right)}^k\right]=e^{k{\mu }_{mn}{\left(l\right)}^{+k^2{\sigma }_{\theta }^2/2}}$$[8]로 주어진다.

Ⅲ. ZF 기반의 수신기 기술

본 논문에서는 초광대역 실내 로그-정규 분포 성질을 가지는 주파수 선택적 다중경로 페이딩 채널에서 2PAM을 사용하는 공간다중화 UWB 무선통신 시스템을 위한 MIMO 검출 기법들을 다룬다. 여기서 수신기의 낮은 복잡도를 위하여 ZF 검출 기법에 집중하여 성능 평가 및 비교 분석을 수행한다. 우선 이전에 제시된 2가지 종류의 ZF 수신기 기반의 신호 검출 기법들을 간략하게 소개하고, 본 논문에서 추가적으로 소개되는 ZF 수신기 구조에 대한 설명과 이론적인 성능 분석 결과를 제시한다.

3.2 2Rake-ZF 수신기

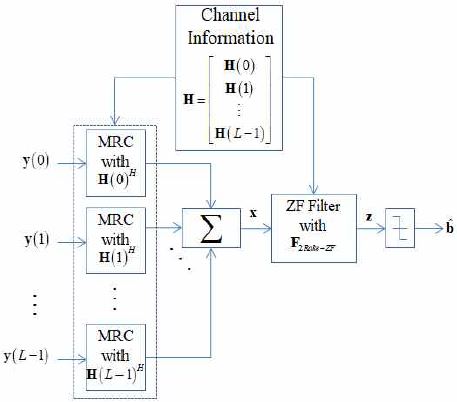
참고문헌 [8]에서 제시된 ZF-Rake 수신기 구조보다 더욱 향상된 다양성 이득을 얻기 위해서 참고문헌 [10]은 그림 2와 같이 시간 및 공간 영역에서 2차원 Rake-MRC를 한 개의 ZF 필터 적용 전에 사용하는 2Rake-ZF 수신 기법을 제안했다. l번째 경로에 해당하는 수신 신호 벡터 y(l)에 대해 공간 결합을 통하여 공간 이득을 얻은 후 모든 다중경로 성분에 대해 다중경로 결합을 수행한다. 시간 및 공간 영역에서 2Rake-MRC를 수행한 수, N_t개의 송신 안테나로부터 전송된 데이터 스트림을 공간적으로 분리하기 위해 ZF 필터를 사용한다[10]. 이 때 2Rake 출력 신호 벡터 $$ \mathit{x}\left(={\sum }_{l=0}^{L-1}\mathit{H}{\left(l\right)}^H\mathit{y}\left(l\right)\right)$$의 ZF 필터링 후의 신호 결정 변수 벡터는 다음과 같이 주어진다[10].

Fig. 2.

2Rake-ZF receiver structure for spatial multiplexing UWB-MIMO system

$\[ z={\mathit{F}}_{2Rake-ZF}\mathit{x} \]$

(3)

여기서 2Rake-ZF 수신기의 ZF 필터 행렬 F_2Rake-ZF와 L개의 다중경로 성분을 모두 포함하는 L_Nr×N_t채널 행렬 H는 각각 다음과 같다[10].

$\[ F_{2Rake-ZF}={\left({\mathit{H}}^H\mathit{H}\right)}^{†} \]$

(4)

$\[ \mathit{H}={\left[\mathit{H}{\left(0\right)}^T\mathit{H}{\left(1\right)}^T\cdots \mathit{H}{\left(L-1\right)}^T\right]}^T \]$

(5)

(N_t,N_r,L) UWB 공간다중화 MIMO 통신시스템에서 2Rake-ZF 수신기를 사용하면 ZF-Rake의 G_ZF-Rake= L(N_r - N_t + 1)값보다 훨씬 큰 G_2Rake-ZF = LN_r - N_t + 1로 주어지는 다양성 이득이 제공된다[10].

3.3 eZF 수신기

본 논문에서는 2Rake-ZF와 ZF-Rake 수신기처럼 다중경로 결합이나 수신안테나 다양성 결합을 위한 Rake-MRC 수신기 구조를 채택하지 않으면서 2Rake-ZF 수신기와 동일한 성능을 나타낼 수 있는 ZF 수신기만을 사용하는 구현이 간단한 구조에 대해 다양성 이득과 그에 따른 BER 성능 분석을 이론적으로 수행한다. 이를 위해 N_r개의 수신안테나와 L개의 다중경로 성분으로부터의 수신신호를 모두 받은 다음, 그림 3과 같이 (5)에서 주어진 행렬처럼 하나의 확장된 큰 채널 행렬을 만들어서 바로 ZF 필터링을 수행한다. 이 수신기는 Rake-MRC 수신부 없이 처음부터 모든 수신 경로 성분들을 고려하여 수행하므로 마치 수신안테나의 개수가 LN_r인 만큼의 수신다양성을 제공받을 수 있게 된다. 이러한 eZF 수신기 구조는 ZF 선형수신기만을 활용하면서 간단하게 채널을 확장해서 사용한다.

Fig. 3.

Proposed eZF receiver structure for spatial multiplexing UWB-MIMO system

eZF 수신기에서 사용될 수신신호 벡터는 다음과 같이 주어진다.

$\[ \mathit{y}=\sqrt{E_b}\mathit{H}\mathit{b}+\mathit{W} \]$

(6)

여기서 LN_r × 1 벡터 y와 w는 다음과 같다.

$\[ \mathit{y}={\left[\mathit{y}{\left(0\right)}^T\mathit{y}{\left(1\right)}^T\cdots \mathit{y}{\left(L-1\right)}^T\right]}^T \]$

(7)

$\[ \mathit{w}={\left[\mathit{w}{\left(0\right)}^T\mathit{w}{\left(1\right)}^T\cdots \mathit{w}{\left(L-1\right)}^T\right]}^T \]$

(8)

그리고 LN_r × N_t채널 행렬 H는 (5)와 동일하게 주어진다. 이 때 확장된 ZF 필터 행렬은 다음과 같다.

$\[ {\mathit{F}}_{eZF}={\mathit{H}}^{†} \]$

(9)

위의 확장된 ZF 필터 행렬을 사용하여 얻어지는 수신기 필터 출력 신호 벡터의 결정 변수는 다음과 같다.

$\[ \mathit{a}={\mathit{F}}_{eZF}\mathit{y}=\mathit{b}+{\mathit{H}}^{†}\mathit{w} \]$

(10)

여기서 평균 비트 에너지 E_b는 1이라 가정한다.

n번째 송신안테나로부터 전송된 데이터 스트림에 대한 순시적인 잡음 전력은 식 (10)으로부터 다음과 같이 얻을 수 있다.

$\[ {\left[E\left\{\left({\mathit{H}}^{†}\mathit{w}\right){\left({\mathit{H}}^{†}\mathit{w}\right)}^H\right\}\right]}_{nn}=\left(\frac{N_0}{2}\right){\left[{\left({\mathit{H}}^H\mathit{H}\right)}^{-1}\right]}_{nn} \]$

(11)

여기서 행렬 H^HH은 full rank 라고 가정한다. 그러면 후처리 SNR(post-processing Signal-to-Noise Ratio)은 다음과 같이 표현될 수 있다[8].

$\[ \begin{array}{cc}SN{R}_{n,eZF}\hfill & =\frac{2}{N_0{\left[{\mathit{H}}^H\mathit{H}\right]}_{nn}^{-1}}=\frac{2}{N_0}{\mathit{h}}_{\mathit{n}}^{\mathit{H}}\prod {\mathit{h}}_{\mathit{n}}\hfill \\ & =\frac{2}{N_0}{\mathit{h}}_{\mathit{n}}^{\mathit{H}}\mathit{U}\mathit{\Lambda }{\mathit{U}}^{\mathit{H}}{\mathit{h}}_{\mathit{n}}=\frac{2}{N_0}{\mathit{h}}_{\mathit{n}}^{\mathit{H}}\mathit{\Lambda }{\mathit{h}}_{\mathit{n}}\hfill \end{array} \]$

(12)

여기서 h_n는 H의 n번째 열로 다음과 같다.

$\[ {\mathit{h}}_n={\left[{\mathit{h}}_n{\left(0\right)}^T{\mathit{h}}_n{\left(1\right)}^T\cdots {\mathit{h}}_n{\left(L-1\right)}^T\right]}^T \]$

(13)

그리고 Π(=UΛU^H)는 h₁,⋯,h_n-1,h_n+1,⋯,h_Nt로부터 구성된 LN_r×LN_r 크기를 가진 nonnegative Hermitian 행렬로 다음과 같이 주어진다.

$\[ \prod =\frac{{\mathit{H}}_n{\mathit{H}}_n^H}{\text{det}\left[{\mathit{H}}_n^H{\mathit{H}}_n\right]} \]$

(14)

여기서 H_n는 행렬 H에서 열벡터 h_n을 제외한 행렬을 나타낸다. 또한, $$ \Lambda =diag\left[{\lambda }_n^{\left(1\right)}{\lambda }_n^{\left(2\right)}\cdots {\lambda }_n^{\left(L{N}_r\right)}\right]$$이고, $$ {\lambda }_n^{\left(i\right)}$$는 행렬 Π의 고유치이다.

그리고 x_n은 x_n = U^Hh_n이고, $$ x_n={\left[x_n^{\left(i\right)}{x}_n^{\left(2\right)}\cdots x_n^{\left(L{N}_r\right)}\right]}^T$$로 표현될 수 있으며, U는 unitary 행렬이다. x_n = U^Hh_n의 통계적인 특성을 얻기 위해서 참고문헌 [8]에 수행된 이론적인 분석 방법을 따라 할 수 있다. 여기서 다중경로 성분들의 전력은 동일하다고 가정한다. 따라서 x_n의 각 원소는 평균이 0이고 분산이 1인 가우시안 랜덤 변수로 근사화할 수 있다.

그림 4는 (N_t,N_r,L)= (3,4,2) 공간다중화 UWB-MIMO 시스템에서 x_n⁽¹⁾에 대해 MATLAB시뮬레이션을 통해 얻어진 히스토그램과 근사화된 확률밀도함수 pdf(probability density function)를 나타내고 있다. 여기서 로그-정규 분포 페이딩 진폭의 표준편차는 참고문헌 [8]에서와 같은 환경으로 5dB라고 가정한다.

Fig. 4.

Approximated pdf of xni in the (Nt,Nr,L)= (3,4,2) spatial multiplexing UWB-MIMO system

참고문헌 [8]과 [11]에서 사용된 동일한 근사적인 분석 방법을 사용하여 행렬 Π의 고유치들 중에서 LN_r - N_t + 1개수의 고유치는 1이고, 나머지 N_t - 1개수는 0 인 것을 입증할 수 있다. 따라서 n번째 송신안테나로부터의 데이터 스트림의 출력 SNR은 다음과 같이 표현된다.

$\[ SN{R}_{n,eZF}=\frac{2}{N_0}\sum _{i=1}^{L{N}_r-N_t+1}{\left|x_n^{\left(i\right)}\right|}^2 \]$

(15)

따라서 eZF 수신기를 사용하는 (N_t,N_r,L) 공간 다중화 UWB-MIMO 시스템의 다양성 이득은 G_eZF =LN_r - N_t + 1로 주어지고, 2Rake-ZF 수신기의 다양성 이득 G_2Rake-ZF와 동일함을 알 수 있다. SNR_n,eZF는 자유도가 G_eZF = LN_r - N_t + 1인 central Chi-square 분포 특성을 나타내는 랜덤 변수이다. 이 때 SNR_n,eZF의 pdf는 감마 함수 Γ(⋅)를 사용하여 다음과 같다.

$\[ {\mathit{f}}_{SN{R}_{n,eZF}}\left(t\right)=\frac{1}{2^{0.5G_{eZF}}\left(0.5G_{eZF}\right)}{t}^{0.5G_{eZF}^{-1}{e}^{0.5t}} \]$

(16)

그러므로 로그-정규 페이딩 채널에서 eZF 수신기의 이론적인 평균 BER 성능을 다음과 같이 계산된다.

$\[ {BER}_{b,eZF}={\int }_0^{\infty }{P}_{b|SN{R}_{n,eZF}}\left(t\right)f_{SN{R}_{n,eZF}}\left(t\right)dt \]$

(17)

여기서 P_b|SNRn,eZF(t)는 조건부 BER을 나타내며, $$ P_{b|SN{R}_{n,eZF}}\left(t\right)=0.5erfc\left(\sqrt{\left(E_b/N_0\right)}t\right)$$으로 주어진다.

Ⅳ. 시뮬레이션 결과

4.1 전력소비량 및 생산량 분석결과

(N_t,N_r,L) 공간다중화 UWB-MIMO 시스템의 모든 시뮬레이션에서 데시벨(decibel) 단위로 비트당 SNR을 참고문헌 [8]에서처럼 SNR_b = E_b/N₀(dB) + 10log₁₀G와 같이 정의하여 사용한다. 여기서 G는 UWB-MIMO 수신기의 다양성 이득을 나타낸다. 즉, ZF-Rake 수신기는 G = G_ZF-Rake = L(N_r - N_t + 1)이고, 2Rake-ZF와 eZF는 G = G_2Rake-ZF =G_eZF=LN_r - N_t + 1로 주어진다.

본 논문에서는 분석의 편의를 위해 E_b를 1로 가정했다. 로그-정규 분포 페이딩 채널 시뮬레이션을 위해서 20log₁₀η_mn(l) (= θ_mn(l)(20log₁₀e))의 표준편차는 5dB를 사용한다[8]. l번째 경로의 평균 전력은 power decay factor γ를 사용하여 E[η_mn(l)²] = e^γl로 주어지는데, 2장에서 언급된 η_mn(l)의 k번째 모멘트 수식과 비교하면, μ_ηmn(l) =-$$ {\sigma }_{\theta }^2$$ - γl/2을 얻을 수 있고, 여기서 σ_θ = 5/(20log₁₀e)임을 알 수 있다[8].

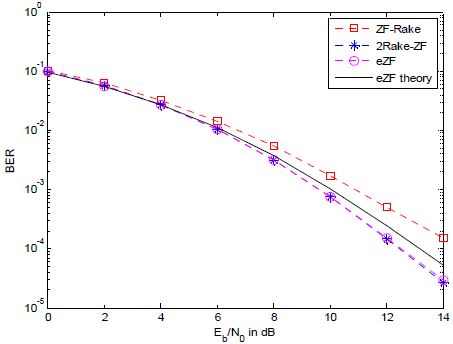
본 논문에서 0번째 경로 성분의 평균 전력은 1이라고 가정하고, γ = 0로 주어진다. 수신기 측에서는 L개의 다중경로 채널에 관한 정보를 알고 있다고 가정한다. 다음의 모든 그림에서 이론적인 분석에 의해 얻어진 평균 BER 곡선과 시뮬레이션을 통해 얻어진 BER 곡선은 각각 선(Line)과 마커(Marker)를 사용하여 나타내고 있다. BER 성능 곡선을 표현하는 그림에서 가로축은 E_b/N₀(dB)를 나타낸다.

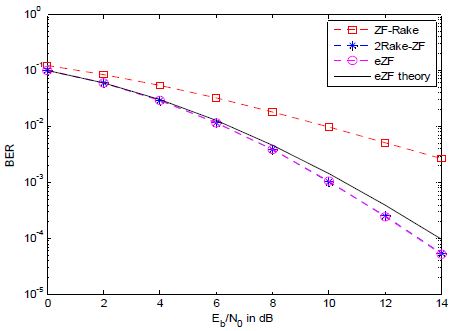
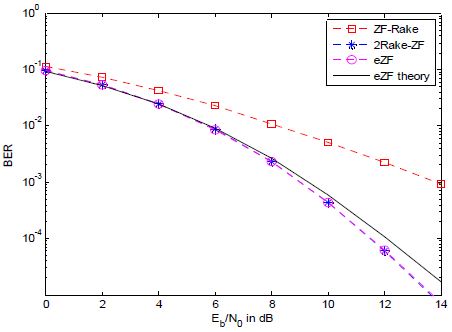
그림 5, 그림 6, 그림 7은 N_t = 3와 N_r = 3인 공간다중화 UWB MIMO 시스템에서 다중경로 수가 L = 2, L = 3, L = 4일 때 ZF-Rake[8], 2Rake-ZF[10], eZF 수신기 구조의 평균 BER 성능 곡선들을 나타내고 있다. 다중경로의 수가 증가함에 따라 BER 성능이 향상됨을 알 수 있다. 그리고 eZF 수신기는 E_b/N₀(dB)가 8dB 보다 큰 영역에서는 ZF-Rake 수신기보다 4dB 이상의 우수한 BER 성능을 나타내고 2Rake-ZF 수신기와 거의 동일한 BER 성능을 보이고 있다. ZF-Rake와의 큰 성능 차이는 eZF 수신기의 다양성 이득 G_eZF =LN_r - N_t + 1= 3L - 2와 ZF-Rake의 다양성 이득 G_ZF-Rake =L(N_r - N_t + 1)= L의 차이가 2L - 2 만큼 나기 때문에 발생했다고 볼 수 있다[8]. 또한 낮은 E_b/N₀영역에서는 이론적인 성능 곡선이 시뮬레이션 결과와 잘 일치하나 E_b/N₀ 값이 큰 영역에서는 약간 차이가 있음을 확인할 수 있다.

Fig. 5.

BER comparison of ZF-Rake, 2Rake-ZF and eZF detection schemes in the (3,3,2) systems

Fig. 6.

BER comparison of ZF-Rake, 2Rake-ZF and eZF detection schemes in the (3,3,3) systems

Fig. 7.

BER comparison of ZF-Rake, 2Rake-ZF and eZF detection schemes in the (3,3,4) systems

Fig. 8.

BER comparison of ZF-Rake, 2Rake-ZF and eZF detection schemes in the (3,4,2) systems

Fig. 9.

BER comparison of ZF-Rake, 2Rake-ZF and eZF detection schemes in the (3,5,2) systems

그림 5, 그림 8, 그림 9는 다중경로 수가 L = 2인 페이딩 채널에서 N_t = 3인 공간다중화 UWB-MIMO 시스템에서 수신안테나 수가 N_r = 3, N_r = 4, N_r = 5일 때 ZF-Rake[8], 2Rake-ZF[10], eZF 수신기 구조의 평균 BER 결과들을 보여주고 있다. 수신안테나 수가 커짐에 따라 수신 다양성 정도가 늘어나기 때문에 BER 성능도 증가하고 있는 것을 확인할 수 있다. 여기서도 다양성 이득에 있어서 G_eZF = G_2Rake-ZF = 2N_r - 2와 G_{ZF -Rake} = 2N_r - 6의 차이가 4이기 때문에, 그림 8에서는 E_b/N₀(dB)가 10dB 보다 높은 영역에서 3dB 이상의 BER 성능을 보이고, 그림 9에서는 E_b/N₀(dB)가 12dB 보다 높은 영역에서 eZF 수신기의 성능이 ZF-Rake 수신기 성능보다 2dB 이상 차이 나는 것을 볼 수 있다. 그리고 이론적인 성능 곡선은 낮은 E_b/N₀ 영역에서는 시뮬레이션 결과와 잘 일치하나 E_b/N₀ 값이 6dB 이상 큰 영역에서는 약간 차이가 있음을 확인할 수 있다.

Ⅴ. 결 론

본 논문에서는 로그-정규 분포 특성을 가지는 실내 다중경로 페이딩 채널 환경에서 공간 다중화된 UWB 신호들을 검출하기 위한 ZF 필터 기반의 수신기 구조들에 대해 이론적인 분석을 통해 얻어진 다양성 이득과 평균 BER 성능들을 비교 평가하였다. 본 본문에서 기술된 eZF 기반 수신기는 Rake MRC 구조를 채택하지 않으면서 LN_r - N_t + 1이라는 다양성 이득을 제공할 수 있으며, 이 결과는 2Rake-ZF 수신기의 다양성 이득과 동일하였다. MATLAB을 이용하여 수신 가능한 경로수와 수신안테나수가 다를 경우를 가정한 시뮬레이션 결과에서는 구현이 간단한 eZF 수신기는 ZF-Rake 수신기보다 우수한 성능을 나타내고, 2Rake-ZF 수신기와는 이론적인 평균 BER 성능도 서로 일치함을 분석하였다.

향후에는 본 논문에서 제안된 수신구조를 기반으로 다른 MIMO 수신기에 적용하여 다양한 환경에서 최적의 성능을 가지는 수신기를 개발하여 구현 및 테스트를 통해 검증하는 연구를 진행할 계획이다.

Acknowledgments

본 논문은 동아대학교 교내연구비 지원에 의하여 연구되었음.

References

• S. Gishkori, V. Lottici, and G. Leus, "Compressive Sampling-Based Multiple Symbol Differential Detection for UWB Communications", IEEE Trans. Wirel. Commun., 13(7), p3778-3790, Jul), (2014. [https://doi.org/10.1109/twc.2014.2317175]
• J. N. Bae, Y. H. Choi, and J. Y. Kim, "Performance Analysis of TH-PPM UWB System for Positioning in Indoor Environment", The Journal of the Institute of Internet, Broadcasting and Communication(JIIBC), 10(3), p153-158, Jun), (2010.
• S. Pisa, E. Pittella, and E. Piuzzi, "A survey of radar systems for medical applications", IEEE Aerospace and Electronic Systems Magazine, 31(11), p64-81, Dec), (2016. [https://doi.org/10.1109/maes.2016.140167]
• E. G. Larsson, F. Tufvesson, O. Edfors, and T. L. Marzetta, "Massive MIMO for next generation wireless systems", IEEE Commun. Mag., 52(2), p186-195, Feb), (2014. [https://doi.org/10.1109/mcom.2014.6736761]
• H. Papadopoulos, C. Wang, O. Bursaioglum, X. Hou, and Y. Kishiyama, "Massive MIMO technologies and challenges towards 5G", IEICE Trans. Commun., E99-B(3), p602-621, Mar), (2016. [https://doi.org/10.1587/transcom.2015ebi0002]
• T. Kaiser, F. Zheng, and E. Dimitrov, "An overview of ultra-wide-band systems with MIMO", Proc. IEEE, 97(2), p285-312, Feb), (2009. [https://doi.org/10.1109/jproc.2008.2008784]
• J. Kim, and J. Y. Kim, "Performance of Rake Receiver for Pulse Position Modulation-Time Hopping Ultra Wide Band Systems in indoor Environments", The Journal of the Institute of Internet, Broadcasting and Communication(JIIBC), 10(3), p179-184, Jun), (2010.
• H. Liu, R. C. Qiu, and Z. Tian, "Error performance of pulse-based ultra-wideband MIMO systems over indoor wireless channels", IEEE Trans. Wirel. Commun., 4(6), p2939-2944, Nov), (2005.
• J. An, and S. Kim, "Performance Analysis of UWB MIMO System with Prerake Transmit Processing", Journal of KIIT, 8(9), p43-50, Sep), (2010.
• J. An, and S. Kim, "Spatial- temporal combining-based ZF detection in ultra-wideband communications", IEICE Trans. Fundam., E92-A(7), p1727-1730, Jul), (2009. [https://doi.org/10.1587/transfun.e92.a.1727]
• J. H. Winters, J. Salz, and R. D. Gitlin, "The impact of antenna diversity on the capacity of wireless communications", IEEE Trans. Commun., 42(2/3/4), p1740-1751, Feb/Mar/Apr), (1994.