RNN을 이용한 범용 예측 시스템 구현
*Continental Automotive Systems**제주한라대학교 컴퓨터정보과 교수
초록
딥러닝은 다양한 알고리즘과 모델이 개발되었으며, RNN(재귀신경망, Recurrent Neural Network)은 미래 예측시스템 분야에서 탁월한 성능을 나타내고 있다. 본 논문에서는 RNN과 LSTM을 적용한 범용 예측 시스템을 구현하였고, cost 값을 측정하여 성능을 평가하였다. 본 연구에서는 입력 데이터간의 차이가 너무 클 경우 원 데이터를 정규화 데이터로 변환시켜 사용하였고, 학습 입력 시퀀스(Sequence) 크기는 5로 하여 성능 실험을 하였다. 학습과 예측 실행 결과와 cost 값은 실시간 그래프로 표시하여 결과의 가독성을 높였다. 실험에서 cost 값은 학습 수 150에서 cost 값이 0.085로 감소하여 학습이 잘 되었다. 단시간의 짧은 학습 횟수로 학습 목표값과 테스트 목표값을 정확하게 학습하고, cost 값이 원하는 수준으로 감소하여 제안한 예측 시스템의 성능이 우수한 것을 실험으로 확인하였다.
Abstract
Various algorithms and models of deep learning were developed, and RNN shows good performance in future prediction system. RNN and LSTM applied universal prediction system was realized in this paper, and performance was evaluated by cost value. Difference between input data was so big that we normalized this input data, and sequence size of learning input was 5 in the performance experiment. The legibility of the results was increased by displaying learning result, predictive execution result and cost values on a real-time graph. In this experiment, accomplishment of learning was confirmed by cost values decrease from learning number 150 to 0.085. future prediction system precisely learned learnin target value and test target value in a small number of learning time in a short time. Furthermore, cost value decreased to wanted value, confirming that the performance of suggested prediction system is excellent.
Keywords:
deep learning, RNN, LSTM, CNN, artificial intelligence, prediction systemⅠ. 서 론
기계학습(Machine Learning)은 준비된 데이터를 가지고 기계가 데이터의 특성을 스스로 학습하여 분류해 결과물을 산출하고 예측하는 것이다. 딥러닝(Deep Learning)[1]은 인공지능에 속한 머신러닝의 일종으로서 은닉층을 여러 개 이상 구성한 다층신경망 모델을 구축한 것으로 이 모델을 학습하는 것이 딥러닝이다. 딥러닝은 입·출력 사이에 여러 개의 층(Layer)을 만들어 어떠한 문제를 해결한다. 대표적인 딥러닝 모델은 재귀신경망(RNN, Recurrent Neural Network)과 합성곱신경망(CNN, Convolutional Neural Network) 등이 있다. RNN은 시간의 진행에 따라 매 순간마다 신경망을 구성하는 구조로 음성인식 등의 예측 시스템 분야에 우수한 성능을 나타낸다. 이미지 인식 분야에 탁월한 CNN은 이미지를 이해하고 고수준의 추상화된 정보를 추출하거나 다양한 영상처리 인식, 컴퓨터 비전 분야에 많이 연구되고 있다. 딥러닝의 다층 신경망에서 출력층 뉴런만 시그모이드 함수를 사용하고 다른 은닉층 출력 뉴런은 ReLU 함수를 사용한다.
비선형적인 문제를 예측하는 것은 어려운 것이지만 기계학습 분야의 인공지능을 이용하여 목적값의 근사치에 쉽게 도달한다는 연구 결과들이 제시되고 있다[2]-[6]. 딥러닝은 인간의 뇌구조를 모방한 인공신경망(ANN, Artificial Neural Network) 학습으로서 기존의 인공신경망 문제점을 보완하여 미래예측, 이미지 인식, 음성인식 등의 다양한 분야에 이용된다. 딥러닝은 다른 형태의 기계학습 방법과는 다르게 입력 데이터의 특징을 그대로 학습하므로 입력 데이터의 특징에 의하여 예측 결과에 큰 차이를 나타낸다[6].
본 연구에서는 J관광도시의 월별 방문 관광객 데이터를 CSV 파일로 데이터베이스화하고 파이썬(Python) 언어를 사용하여 자체 개발한 프로그램으로 필요한 부분의 데이터를 추출하였다. 인공지능 개발 라이브러리인 텐서플로우(TensorFlow)를 이용하여 구현하였고 예측 시스템 개발을 위해 심층신경망(DNN, Deep Meural Network), RNN, LSTM(Long Short Term Memory) 등을 사용하였다[7][8]. 예측 시스템에서는 DNN보다 시계열 딥러닝 네트워크 LSTM과 RNN을 사용한 경우가 예측율이 높고 안정적이며 빠르게 학습된다[9] 개발한 예측 시스템에 관광객 데이터를 학습 입력으로 하여 시스템의 성능을 평가하였다. 본 연구는 제 1장 서론, 제 2장 기술분석, 제 3장 범용 예측 시스템, 제 4장 실험 및 결과, 제 5장 결론 및 향후 과제에 대하여 기술하였다.
Ⅱ. 기술 분석
기존의 전통적인 신경망은 입력 데이터가 모두 독립적으로 학습되어 시간에 따라 정보를 학습시키는데 한계가 있다. RNN은 시간에 따른 순차적인 정보를 학습시키는 알고리즘으로서, 입력 데이터가 모두 같은 과정을 반복하므로 이전의 모든 계산 정보는 현재의 예측 결과에 적용된다. 기존의 전형적인 RNN 알고리즘은 하나의 ReLU 또는 tanh 함수를 가진 구조로 체인이 길면 과거의 학습 결과가 사라지는 장기의존성 문제를 가지고 있었다. 이를 해결하기 위한 것이 LSTM이다. 본 논문에서 사용한 NN, RNN, LSTM은 다음과 같다.
2.1 NN
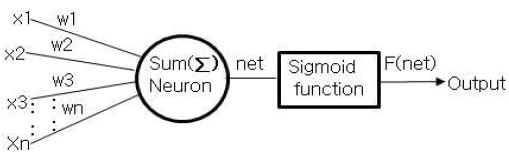
신경세포(Neuron)의 인공적인 처리기 구성은 그림 1과 같으며 신경망은 반복학습에 의해 원하는 지식을 습득한다.
학습 의미는 학습오차가 원하는 수준으로 감소할 때까지 연결가중치(Weight)를 조정하는 것이다. 그림 1에서 뉴런의 출력값 net는 모든 입력의 합(Σ)의 동작으로 식 (1)로 표현되고 뉴런의 실제 출력값 f(net)은 net값에 시그모이드 함수를 취하여 식 (2)와 같이 구한다.
| (1) |
| (2) |
2.2 RNN
RNN과 CNN은 같은 신경망을 여러 개 복사해서 병렬 체인 구조로 연결하여 이전 신경망의 학습결과를 현재 신경망의 학습에 사용하는 구조이므로 과거 시점의 데이터를 이용하여 현재를 예측할 수 있어 시계열 데이터를 처리하는데 매우 효과적인 알고리즘으로서[10][11] 음성인식, 번역, 언어모델, 동영상, 로그데이터, 시계열의 통계 데이터와 같은 연속적인 데이터 처리에 탁월한 성능을 나타낸다. 기존의 전통적인 신경망은 입력 데이터가 독립적으로 학습되므로 시간의 흐름에 따라 정보를 학습하는데 한계가 있었다. RNN은 모든 입력 데이터가 같은 과정을 반복하고, 이전의 모든 계산 정보는 현재의 예측 결과에 적용되므로 현재의 데이터를 가지고 다음의 상태를 예측하는 시스템에 우수한 기능을 가진다.
RNN은 그림 2와 같은 구조로 은닉상태 노드(Hidden State Node)가 방향을 가진 엣지((Edge)로 연결된 재귀구조로 구성되므로, 상태를 계산 후 자기입력을 하고, 이전 데이터가 다음에 영향을 미친다. 그림 2에서 시간정보 t와 웨이트 W값을 추가하면 이 W값을 통해 이전 데이터가 다음에 영향력을 끼치거나 영향을 받는 것이다. 즉, Xt는 t시간에서의 입력값, Wxh는 인코딩을 위한 웨이트로 벡터값, Ht는 인코딩한 결과, Whh는 Ht에서 우측 엣지의 웨이트값, Wyh는 디코딩 하기 위한 웨이트로 벡터값, yt는 t시간에서의 디코딩 결과 출력으로서 예측값이며, 예측된 출력값 yt는 Wyh의 값에 의하여 결정된다. 그림 2에서 학습을 위한 웨이트의 집합은 하나의 cell 안에 다 있고 모든 cell에서 공유된다. 그림 2의 RNN 모델에서 ht는 식 (3)과 같이 쓸 수 있다.
| (3) |
여기서 ht는 다음의 새로운 상태를 계산하는 식, fw는 파라메터 w를 가지는 함수, xt는 어떤 시간에서의 입력으로 벡터값, ht - 1은 이전 상태 값이다. 위 식 (3)은 식 (4)와 같이 쓸 수 있고, yt는 식 (5)와 같이 쓸 수 있다.
| (4) |
| (5) |
여기서 whh는 은닉층 웨이트 값, ht - 1은 이전 상태 값, wxh는 입력층 웨이트로 벡터값, xt는 어떤 시간에서의 입력으로 벡터값, yt 는 t시간에서 출력한 예측값, wyh는 출력 웨이트로 벡터값이다.
RNN은 상태를 계산하여 출력한 후 자기입력으로 가지는 구조로서 여러 종류의 형태가 개발되어 제공되고 있으며 향상된 대표적인 모델이 LSTM과 GRU(Gated Recurrent Unit)이다. LSTM은 학습이 이뤄지는 역전파에서 cost 값이 잘 유지되고 전달되게 만든 것이다. RNN은 이전의 정보를 가지고 공유하고 활용할 수 있지만 시간의 간격(Gap)이 크지 않을 경우에 가능하다. RNN은 시간의 간격이 크면 과거의 학습 결과가 사라지는 기울기 소실(Vanishing Gradient)로 장기의존성 때문에 사용할 수 없다. 이 문제를 해결하기 위한 것이 LSTM이며 LSTM은 장기 의존성 문제를 해결할 수 있는 것으로서 1997년에 Hochreiter가 제안하였다.
2.3 LSTM
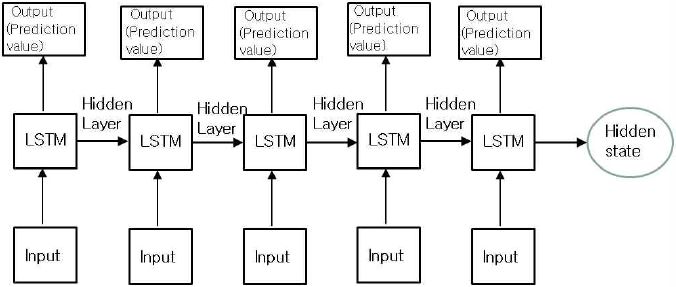
LSTM의 핵심은 딥러닝 네트웍이 깊어질수록 초기 에러값이 점점 사라지는 것을 해결하기 위해 셀스테이트(Cell State)를 가지는 구조이다. LSTM은 그림 3과 같이 전체 체인을 지나가는 셀 스테이트를 가진 구조를 이용하여 과거의 학습결과를 현재 학습에 그대로 전달하여 RNN의 장기 의존성 문제를 해결하였다. 그림 3의 LSTM 구조에서 셀 스테이트와 은닉층(Hidden Layer) tanh가 별도로 존재한다.
셀 스테이트는 forget gate와 input gate를 거친 후 다음 상태로 이동하는데 주로 정보 기억을 담당하고, forget gate는 Cell상에서 크게 중요하지 않은 정보를 삭제한다. LSTM은 첫째 시그모이드 함수를 사용하여 삭제할 정보를 결정, 둘째 또 다른 시그모이드 함수와 tanh 함수를 사용하여 새로운 정보를 셀 스테이트에 저장할지 결정, 셋째 셀 스테이트를 갱신, 넷째 마지막 시그모이드 함수와 셀 스테이트에서 나오는 출력을 통과한 마지막 tanh 함수로 어떤 값을 출력할지를 결정한다[12][13].
그림 3에서 Forget Gate Layer는 식 (6)과 같다.
| (6) |
Input Gate Layer는 식 (7)과 같이 쓸 수 있고, 는 식 (8)과 같이 쓸 수 있다.
| (7) |
| (8) |
Update Cell State는 식 (9)와 같이 쓸 수 있다.
| (9) |
Output Gate Layer는 식 (10), ht는 식 (11)과 같이 쓸 수 있다.
| (10) |
| (11) |
텐서플로우에서 그림 3의 방식으로 사용하는 LSTM의 구현 클래스는 다양한 종류가 있지만 본 논문에서는 아래 ①을 이용하였다.
① BasicLSTMCell
tf.contrib.rnn.BasicLSTMCell
= tf.nn.rnn_cell.BasicLSTMCell
이 클래스는 Forget Bias가 default = 1.로 설정되어 있으며, Peep Hole, Projection Layer, Cell Clipping을 지원하지 않고, 내부의 Linear 연산을 실행할 때 _linear() 함수를 사용한다.
② LSTMCell
tf.contrib.rnn.LSTMCell = tf.nn.rnn_cell.LSTMCell
이 클래스는 Forget Bias가 default = 1.로 설정되어 있으며, Peep Hole, Projection Layer, Cell Clipping을 지원한다. BasicLSTMCell과 LSTMCell은 같은 파일에 구현되어 있으므로 내부의 Linear 연산을 실행할 때 _linear() 함수를 사용한다.
③ LSTMBlockCell
tf.contrib.rnn.LSTMBlockCell =
tf.nn.rnn_cell.LSTMBlockCell
이 클래스는 Forget Bias가 default = 1.로 설정되어 있고, Peep Hole, Cell Clipping을 지원한다.
2.4 데이터베이스
예측 시스템으로 미래의 데이터를 예측하기 위하여 먼저 관련된 기존 데이터가 있어야 한다. 본 연구의 예측 시스템에서 학습 입력으로 사용하는 데이터는 J관광도시의 관광협회에서 제공하는 기존 관광 방문객 숫자정보 텍스트 데이터를 CSV 파일로 변환하여 사용하였다. 딥러닝 학습에서 많은 양의 데이터를 사용하면 학습시간은 더 걸려도 예측이 더 정확하다. 예측 시스템 학습에서 학습 입력 데이터 차이가 크면 학습이 잘 이루어지지 않으므로 이 경우는 원 데이터를 양자화시켜 입력 데이터 간의 크기 차이를 줄여야한다. 학습 데이터와 테스트 데이터를 분리하는 split_data(data_spt, train_percent=0.80) 함수는 분리된 각각의 데이터를 파이썬의 리스트에 저장한 후 예측 시스템의 학습 입력 데이터로 사용하고 테스트 데이터는 예측이 잘 되는지를 테스트하는 데이터이다.
Ⅲ. 범용 예측 시스템
본 논문에서 제안한 범용 예측 시스템은 RNN과 LSTM을 기반으로 프로그램을 개발하여 구현하였고 순서도는 그림 4와 같다. RNN에서 라벨인 목표값은 학습 입력 데이터 인덱스 다음의 데이터 값, 즉 학습 입력 데이터 인덱스 +1이다. 다시 말해 입력 input에 대한 정답인 목표값은 input+1에 있는 값들이 된다. 예를 들면 [1,2,3,4,5,6,7,8,9]라는 순차 데이터가 있고 입력이 [1,2,3,4,5]이면 정답인 목표값은 [2,3,4,5,6]이다. 즉, [1,2,3,4,5]의 값이 입력이면 6의 값을 찾는 것이다.
그림 4 예측 시스템에서 개발한 Class SeriesPredictor 클래스는 데이터를 학습하고 예측하는 다양한 함수를 포함하며 이 클래스 초기 값으로 입력 값의 차원 수, 순서열 크기(Sequence Size), 은닉 유닛(Hidden Unit)의 차원 수를 인자로 받는다. def__init__(self, input_dim, seq_size, hidden_dim) 함수는 100 차원을 가진 5개의 출력, 하나의 state 값 출력, 각각의 웨이트 값 초기화, cost 및 학습 노드 등을 정의하고 프로그램화 하였다. SeriesPredictor 클래스 내의 model() 함수는 학습 모델을 정의한다. plot_result() 함수는 학습의 진행 과정과 테스트 실행 과정, 예측 결과를 실시간으로 모니터링 하여 그래프로 표시하는 기능이다. 본 논문에서 구현한 범용 예측 시스템 구성도는 그림 5와 같다. 그림 5에서 예측값을 구할 수 있도록 텐서플로우에서 제공하는 BasicLSTMCell을 이용하여, dynamic_rnn() 함수로 RNN을 수행하며, 출력과 상태는 입력에 대한 예측값들과 마지막 은닉 상태 값이다.
그림 5의 예측 시스템에서 미래 데이터를 예측하기 위하여 데이터의 순서열 크기는 5로 하였고, RNN은 100*5(예측 출력의 순서열 데이터)개로 구성한다. 즉, 각각 100차원을 가진 5개의 예측값들이 출력되고, 하나의 state 값이 출력된다. 5*100 차원의 값들을 하나로 합치기 위해 100*1의 웨이트를 행렬 곱한 후 bias를 더한 값과 목표값(Label) 값들을 비교한 차이로 cost 만큼 값을 수정하여 진행한다.
본 연구에서 범용 예측 시스템으로 사용하기 위해서는 학습 데이터 종류(필드)가 여러 개 있는 경우에도 csv 파일을 읽어서 학습하도록 load_series() 함수 내부를 다음과 같이 작성한다.
def load_series(filename ,series_dix=1-4):
data_org = [float(row[series_dix]) for row in
csvreader if len(row) > 0]
여기서는 0열을 제외한 1~4열의 데이터를 추출하는 것이다.
Ⅳ. 실험 및 결과
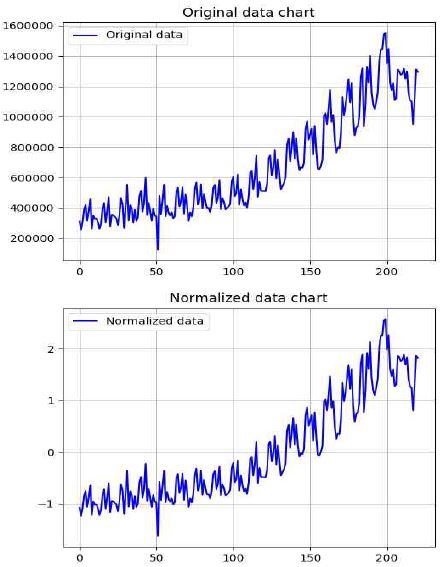
본 논문의 실험 환경은 Windows 10 64비트 운영체제, Python 3.5.2 64비트 버전, Anaconda3-4.2.0, 텐서플로우 1.0을 사용하였다. 본 연구에서 구현한 범용 예측 시스템 성능을 평가하기 위하여 J도시의 관광 방문객 데이터를 2000년 1월부터 2018년 5월까지 221개의 텍스트 데이터를 CSV 파일로 변환시켜 이 중 80%인 177개는 학습 데이터로 사용하고, 20%인 44개는 테스트 데이터로 사용하였다. 학습입력 데이터 최소값은 124,239, 최대값은 1,551,305로 차이가 1,427,066으로 너무 커서 원래의 데이터를 정규화 데이터로 변환시켜 학습하였고, 예측한 후에는 원래의 데이터로 복원하였다. 학습율은 0.0015, 학습 시퀀스 크기는 5, 학습 횟수 조건은 반복 실행문에서 학습을 수행한 현재의 테스트 cost 값이 바로 앞전의 테스트 cost 값 보다 5회 이상 크다면 학습을 종료한다. 즉, 반복문에서 학습이 100번 실행될 때마다 테스트 함수를 실행하여 현재의 테스트 cost 값이 앞전의 테스트 cost 값보다 감소하면 min_test_err 값을 갱신하고, 실행중인 테스트 cost 값이 이전의 테스트 cost 값보다 5번 이상 크면 그 시점에서 학습을 중단시킨다.
예측 시스템이 잘 학습될 수 있도록 xavier 함수를 사용하여 가중치를 초기화시켜 학습율과 학습속도를 빠르게 하였고, AdamOptimizer 알고리즘을 사용하여 오차 감소화를 최적화하였다. 관광객 방문예측 요소는 입력 데이터 시퀀스 크기를 5로 하여 실행 결과의 cost를 확인하였다. 학습 cost는 학습 오차값으로 목표값과 학습한 예측값의 차이다. RNN에서 활성화 함수로 tanh와 ReLU 함수를 사용하였다. train(self, train_x, train_y, test_x, test_y) 함수는 세션 객체를 초기화 한 후, 학습을 100번 실행할 때마다 학습 수, 학습 cost 값, 테스트 cost 값, 예측 값 등을 구해서 표시한다. test(self, sess, test_x) 함수는 테스트 데이터를 사용하여 학습이 잘 되었는지 검증하는 기능이다.
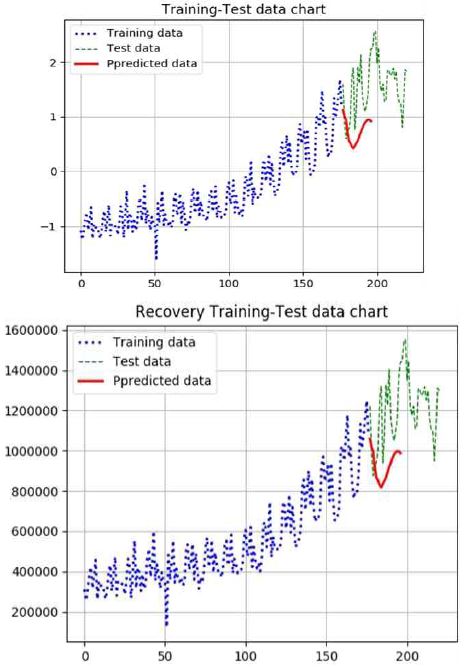
표 1은 학습 입력을 위한 그림 6 상단의 월별 관광 방문객 원 데이터이고, 표 2는 표 1의 원 데이터를 정규화로 변환시킨 그림 6 하단의 값이다. 표 3은 학습에 따른 그림 7의 학습과 테스트 실행 때의 학습 및 테스트 cost 값을 나타내고, 표 4는 학습과 테스트를 완료한 후에 예측 함수가 실행한 그림 7의 예측 데이터 값이다.
그림 6, 그림 7, 그림 8은 본 논문에서 제안한 RNN을 이용한 예측 시스템을 실행한 결과 그래프이다. 그림 6에서 상단 x축은 학습을 위한 입력 원데이터 221개이고 y축은 각각의 입력값을 표시한 그래프이며, 하단은 이 원 데이터를 정규화 데이터로 변환시켜 표시한 그래프이다.
그림 7에서 상단의 굵은 청색 점선은 그림 6 하단의 학습 입력 데이터 80%인 177개 정규화 데이터를 이용하여 학습한 결과의 학습 그래프이다. 이것은 학습함수를 실행한 학습 결과 그래프로 그림 6의 학습 입력 데이터 177개 목표값을 정확하게 학습한 것을 확인할 수 있다. 그림 7에서 가느다란 녹색 점선은 그림 6 하단의 정규화 데이터 20%인 학습 데이터 177개 이후의 44개 테스트 데이터를 사용하여, 테스트 함수를 실행한 테스트 실행 결과 그래프로서 정확하게 테스트 목표값을 수행함으로서 성능이 우수한 것을 확인할 수 있다. 그림 7에서 굵은 빨강색 실선은 예측 함수를 실행하여 미래 방문할 20개월의 예측 결과 데이터 그래프 값이다. 그림 7 하단은 상단의 정규화 데이터를 원 데이터로 변환시킨 그래프이다.
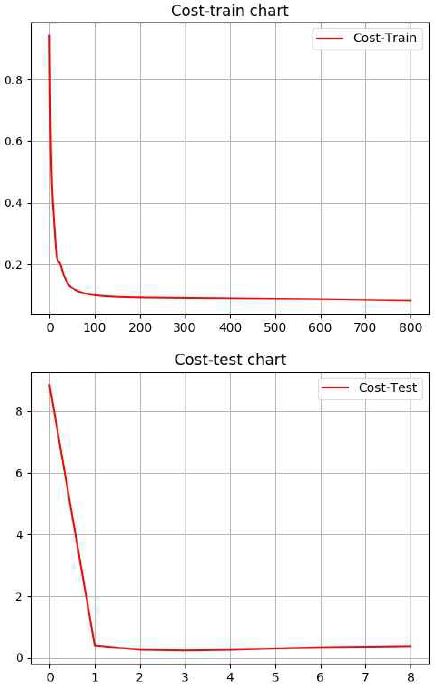
그림 8은 예측 시스템을 실행한 결과의 cost 그래프로서 상단은 학습 때의 학습 cost 값 그래프이다. 그림 8의 상단 그래프에서 알 수 있듯이 그림 6의 177개 학습 입력 데이터를 사용하여 학습이 10회만 진행되어도 cost 값은 0.2로 급격히 감소하고 800번의 학습이 완료된 후에는 0.081로 짧은 학습시간에 학습이 매우 잘 되는 것을 확인할 수 있다. 그림 8의 하단은 그림 6의 테스트 데이터 44개를 사용하여 테스트 함수가 실행한 테스트 cost 값을 표시한 그래프로서 1회만 실행되어도 cost 값이 0.5로 테스트가 잘 진행된 것을 확인할 수 있다.
이 cost 그래프들의 텍스트 값을 표 3에 표시하였다. 위와 같은 실험 결과로 800번의 매우 짧은 학습 시간에 학습 목표값과 테스트 목표값을 정확하게 학습한 것을 각각의 cost 값으로 확인하여 본 논문에서 구현한 예측 시스템의 성능이 우수한 것을 확인하였다.
Ⅴ. 결론 및 향후 과제
본 연구는 인공지능 학습 알고리즘인 RNN과 LSTM에 관광객 방문 데이터를 적용하여 예측 시스템을 연구하였다. 본 논문에서 제안한 범용 예측 시스템은 단 시간의 짧은 학습 횟수로 빠르고도 안정적으로 목표값을 학습한 후, 요구하는 미래의 예측 데이터를 효율적으로 추출하게 된다. 이와 같은 시스템의 시뮬레이션 결과는 그 성능이 우수한 것으로 실험에서 나타났다.
본 예측 시스템을 다양한 예측 분야에 접목하여 여러 분야에서 미래 예측율의 정확도를 높여서 이용할 수 있도록 다양한 분야의 학습 데이터를 입수하고 학습시키는 것을 요구한다. 또한 이 시스템이 여러 예측 분야에 이용할 수 있도록 성능이 더 우수한 범용적인 예측 시스템으로 성능을 개선시키는 것이 차후의 연구 과제이다.
References
- Young-Hyun Kim, Gi-Woong Shin, and Yong-Hwan Lee, "The Forecast of Future Technology Based on Deep Learning", Journal of KIIT, 2015(6), p219-220, Jun), (2015.
- T. Fischer, and C Krauss, "Deep learning with long short-term memory networks for financila market prediction", FAU Discussion Papers in Economics, (11), p310-342, May), (2017.
-
Y. K. Kwon, S. S. Choi, and B. R. Moon, "Stock prediction based on financial correlation", Proceedings of the 7th annual conference on Genetic and evolutions computation, ACM, p2061-2066, Jun), (2005.
[https://doi.org/10.1145/1068009.1068351]

- C. Hsu, "A hybrid procedure for stock price prediction by integrating self-organnizing map and genetic programming", Expert Systems with Applications, 38(11), p14026-14036, Oct), (2011.
- J. W. Lee, "A Stock Trading System based on Supervied Learning of Highly Volatile Stock Price Patterns", Journal of Korean Institute of Information Scientists and Engineers, 19(1), p23-29, Jan), (2013.
- S. M. An, "Deep Learning Architectures and Applications", Korea intelligent information system society, intelligent information study, 22(2), p127-142, Jun), (2016.
- K. J. Jeong, and J. S. Choi, "Deep Recurrent Neural Networks", Communications of the Korean Institute of Information Scientists and Engineerings, 33(88), p39-43, Aug), (2015.
- Giles, C. Lee, S. Lawrence, and A. C. Tsoi, "Noisy time series prediction using recurrent neural networks and grammatical inference", Machine learning, 44(1), p161-183, Jul), (2001.
-
Dong-Ha Shin, Kwang-Ho Choi, and Chang-Bok Kim, "Deep Learning Model for Prediction Rate Improvement of Stock Price Using RNN and LSTM", Journal of KIIT, 15(10), p9-16, Oct), (2017.
[https://doi.org/10.14801/jkiit.2017.15.10.9]

- C. T. Jung, Y. K. Park, and S. E. Lee, "13~14 Year Winter Maxmum Demand Prediction", Korea Electric Power Corporation Economic Research Institute, p12pages, Dec), (2013.
- B. G. Koe, H. S. Kim, H. S. Lee, and J. H. Park, "Short-term Electric Load Forecasting for Summer Season using Temperature Data", The transaction of the korea institute of electrical engineers, 64(8), p1137-1144, Aug), (2015.
- F. A. Gers, N. N. Schraudoph, and J. Schmidhuber, "Learning precise timing with LSTM recurrent networks", Journal of Machine Learning Research 3, p115-143, Mar), (2002.
- S. Selena, M. Nijole, and M. Algirdas, "High-low Strategy of Portfolio Composition using Evolino RNN Ensembles", Inzinerine Ekonomika Engineering Economics 2017, 28(2), p162-169, Apr), (2017.

2016년 8월 : 부산대학교 전자전기공학부(공학사)
2016년 4월 ~ 현재 : Continental Automotive Systems Engineer
관심분야 : 전자회로설계, 제어 및 임베디드시스템, 디지털신호처리, 인공지능

1983년 2월 : 동아대학교 전자공학과(공학사)
1985년 2월 : 동아대학교 전자공학과(공학석사)
1997년 7월 : 동아대학교 전자공학과(공학박사)
2007년 9월 : 부총리겸교육 인적자원부장관상 수상
1994년 ~ 현재 : 제주한라대학교 컴퓨터정보과 교수
관심분야 : 인공지능 및 제어시스템, 임베디드시스템, 통신프로토콜