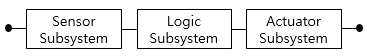IEC 61508 안전 무결성 수준의 정량적 검증
초록
안전 기능은 사고를 일으킬 수 있는 위험요인으로부터 사람의 목숨이나 재산 또는 환경을 지키는 안전 보호 시스템이다. 이와 같은 안전 기능은 가능한 고장 없이 동작해야 한다. 관련된 국제 표준 IEC 61508 에서는 안전 기능의 고장율을 안전 무결성 수준(SIL)으로 정의하고 있다. 따라서 안전 기능을 개발할 때에는, 고장율이 SIL을 만족하는지를 검증해야 한다. RBD, FTA로 검증하는 기존 연구들과는 다르게, 본 논문에서는 SIL 검증을 확률 모델 검증 문제로 간주한다. 개발할 안전 기능을 연속 시간 마코프 체인으로 모델링하고, 연속 확률 논리로 속성을 명세해서, 정량적인 SIL 검증을 수행한다. 본 논문의 유용성을 확인하기 위해서, 탱크 과류 방지를 수행하는 안전 기능에 적용하였다. 그 결과, IEC 61508 공식을 사용하는 것과 같은 결과를 얻었을 뿐만 아니라, RBD와 FTA에서 사용하는 정적 모델과는 달리, 연속 시간 마코프 체인은 동적 모델이기 때문에 시간의 흐름에 따른 고장율 등도 분석할 수 있었다.
Abstract
Safety function is a protection system of human life, economic loss and environmental damage against hazardous events which will cause an accident. Safety function performs its missions when it is demanded without failures if possible. IEC 61508 defines four discrete levels of SIL defining failure rates of safety function. When we develop safety function, SIL verification must be conducted. There has been a number of methods such as RBD and FTA used for quantitative SIL verification. This paper regards quantitative SIL verification as a probabilistic model checking problem. Thus, safety function is modelled as Continuous Time Markov Chain and properties specified as Continuous Stochastic Language. Then, our method is applied to a case study of Tank Overfill Protection in order to demonstrate the validity of our approach. As a result, we obtain the same result compared to formulas in IEC 61508. In addition, we can allow to analysis time-dependent behavior of safety function since Continuous Time Markov Chain is a dynamic model, not a static one like in RBD and FTA.
Keywords:
safety function, safety integrity level, quantitative verification, probabilistic model checkingⅠ. 서론
국제 표준 IEC 61508에 의하면, 안전 기능(Safety Function)이란 사고를 일으킬 수 있는 위험요인으로부터 사람의 목숨이나 재산 또는 환경을 지키는 안전 보호 시스템이다[1]. 안전 기능은 위험요인이 발생되었을 때, 다시 말해서 안전 기능 수행을 요청 받았을 때, 정상적으로 동작해서 시스템을 보호해야 한다. 만약 그렇게 할 수 없다면, 사고가 발생할 수 있다. 위험요인 하에서 안전 기능이 정상적으로 동작할 수 있는 능력 정도를 안전 무결성이라 부르며, 편리를 위하여 일정 구간으로 구분한 것을 안전 무결성 수준(Safety Integrity Level), 줄여서 SIL이라 부른다. IEC 61508에는 SIL 1 ~ SIL 4 네 구간이 사용되며, SIL 1이 가장 낮고, SIL 4가 가장 높다. SIL이 높을수록 안전 기능이 정상적으로 동작할 확률도 높다.
안전 보호 시스템은 여러 개의 안전 기능으로 구성되어 있으며, 각각의 안전 기능 마다 안전 무결성 수준인 SIL이 배정된다. 그러므로 안전 기능을 분석하거나 설계할 때 안전 기능이 SIL을 만족하는지를 평가해야 하는데, 이것을 SIL 검증(SIL Verification)이라고 부른다[2]. SIL 검증에 널리 사용되는 기법에는 신뢰성 블록 다이어그램(RBD, Reliability Block Diagram), 결함 수목 분석(FTA, Fault Tree Analysis) 등이 있다[3][4].
본 논문에서는 SIL 검증 문제를 모델 검증문제로 간주한다. 특히, 안전 기능의 정상적인 동작 능력이나 또는 이것의 반대 개념인 고장율 등은 정성적인 값이 아니라 정량적이기 때문에 본 논문에서는 확률 모델 검증을 사용한다. 그래서 주어진 안전 기능의 동작 행위를 연속 시간 마코프 체인으로 표현하며, 만족해야 할 SIL 속성을 연속 확률 논리로 기술한다. 그런 후에 확률 모델 검증 도구를 통해서 모델이 속성을 만족하는지를 검증한다. 만약 확률 모델 검증을 수행한 결과가 참이라면, 안전 기능의 성능이 SIL을 충족한다는 의미이다. 만약 그렇지 않다면, 안전 기능의 성능이 SIL을 만족하지 못하기 때문에 개선책을 강구해야 한다.
본 연구의 기여는 다음과 같다. 첫째, 본 연구와 비슷하게 SMV 같은 모델 검증 도구를 사용하여 시스템 안전성을 검증하는 연구가 있었다[5]. 그러나 이들 연구는 시스템의 정성적인 측면만 검증하였을 뿐, 성능과 같은 확률적인 값은 추론하지 못했었다. 본 연구에서는 확률을 이용하여 정량적으로 SIL 검증을 수행한다. 둘째, 전통적으로 FTA가 SIL 정량화에 널리 사용되고 있다[6]. FTA는 AND 게이트, OR 게이트 등의 이진 논리를 사용하여 시스템의 고장율을 평가하는 정적 모델이다. 이에 반해서, 본 연구에서는 연속 시간 마코프 체인과 같은 동적 모델을 사용하기 때문에 고장율 뿐만 아니라, 시간에 따른 변화도 분석할 수 있다. 그러므로 이전 연구와 본 연구를 보완해서 사용한다면 더 다양한 측면의 시스템 안전을 고려할 수 있겠다.
본 논문의 구성은 다음과 같다. 2장에서는 안전 기능에 관한 배경 지식을 기술한다. 그리고 3장에서는 확률 모델 검증을 이용한 안전 기능의 SIL 검증 방법을 제안한다. 그런 후에, 제안된 방법을 사례에 적용한 경험을 4장에서 설명한다. 5장에서는 결론과 향후 연구를 기술한다.
Ⅱ. 관련 연구
IEC 61508은 E/E/PE 기술을 이용하여 안전 기능을 분석, 설계, 제작, 운영하는데 널리 사용되는 국제 표준이다[1]. 안전 기능은 서브시스템들로 구성되는데 입력부, 제어부, 출력부가 있다. 입력부는 센서를 통해서 위험요인 발생을 감지한 후에, 이를 제어부에 전달한다. 제어부는 센서에서 받은 값을 비교하여 안전 기능의 실행 여부를 판단한다. 예를 들어, 탱크의 저장 수위가 설정 수위에 도달했는지를 판단하여 그에 상응하는 명령을 출력부에 전달한다. 출력부는 제어부에서 전달된 명령을 실행함으로서 안전 기능을 수행한다.
안전 무결성은 안전 기능의 정상 동작 확률인데, 표준에서는 이것의 반대 개념인 고장 확률, 줄여서 고장율로 안전 무결성을 나타낸다. IEC 61508은 고장율을 두 가지 요청 모드로 구분한다. 즉, 1년에 1회 미만인 낮은 요청 모드와, 그 이상인 높은 요청 모드 또는 연속 요청 모드가 있다. 본 논문에서는 낮은 요청 모드에서의 고장율인 PFD(Probability of dangerous Failure on Demand)를 다룬다. 즉, 위험 요인이 발생되어 안전 기능이 요청되었을 때, 안전 기능이 실패할 위험 고장율로서 표 1과 같다.
IEC 61508에서는 고장을 크게 안전 고장과 위험 고장으로 구분한다. 안전 고장이 발생되면 요청이 없는데도 안전 기능이 작동되는, 소위 오경보(False Alarm)가 발생하지만, 사고로 이어지지는 않는다. 안전 고장보다 심각한 것이 위험 고장이다. 즉, 위험요인이 발생해서 안전 기능의 실행을 요청했는데도, 고장으로 인해서 안전 기능이 작동 못하면 사고가 발생할 수 있기 때문이다. PFD(t)는 특정 시점 (t)에 위험 고장으로 인해서 안전 기능이 수행되지 못할 확률이다.
| (1) |
PFD(t)를 시간의 함수로 표현할 수도 있지만 여기서는 평균값인 PFDavg로 표현한다. 시간 간격 τ로 증명 테스트가 실시되고, 증명 테스트 후에는 시스템 고장이 완전하게 수리되어 마치 “새것처럼(as good as new)” 회복되었다고 가정한다면, 평균 고장율은 다음과 같다.
| (2) |
여기서 R(t)는 신뢰성 함수 또는 생존함수로서, 안전 기능의 정상 동작을 나타낸다. 생존의 반대가 고장이듯이, 신뢰성의 반대는 불신뢰성이다.
| (3) |
여기서 F(t)는 불신뢰성 함수이다. 다루는 고장이 안전 기능의 고장이기 때문에
| (4) |
이다. 식 (2) ~ (4)를 정리하면 다음을 얻는다.
| (5) |
이것이 구하려는 안전 기능의 평균 고장율이다. 안전 기능이 여러 개의 서브시스템들로 구성되기 때문에 전체 고장율은 이들을 모두 더한 값이다.
| (6) |
여기서 PFDSavg, PFDCavg, PFDAavg는 입력부, 제어부, 출력부의 평균 고장율이다.
Ⅲ. 정량적인 SIL 검증
3.1 마코프 모델
본 논문에서는 안전 기능의 고장율을 정량화하기 위해 마코프(Markov) 모델을 사용하며, 모델링은 가이드 IEC 61165를 따른다[7]. 마코프 모델은 시스템의 동적 행위, 특히 고장 및 수리를 모델링하는데 사용된다. 마코프 모델은 상태와 상태간의 전이로 구성된 상태 전이 다이아그램 또는 전이율 행렬(Transition Rate Matrix)로 표현된다. 예를 들어, 그림 2는 상태 3개와 전이 4개로 구성된 마코프 모델이다. 상태 0은 정상이지만 상태 1,2는 고장(Down)이다. 고장 상태를 나타내는 집합을 D라고 하면, D = {1,2}이다. λDD를 발견된 위험 고장이라고 하자. 이러한 고장은 내부 진단에 의해서 수리되며, 이때 걸리는 평균 수리 시간은 MTTR 이다. 한편 λDU를 미발견된 위험 고장이라고 하자. 이러한 고장은 증명 테스트와 같이 외부 점검에 의해서 수리된다. 증명 테스트의 시간 간격을 τ, 증명 테스트에 소요되는 시간이 MRT이면, 평균 수리 시간은 이다.
마코프 모델은 시스템을 상태 기반으로 모델링한 후에 시간의 흐름에 따라서 시스템의 상태 변화를 분석하는 기법이다. 크게 시간 종속적인 분석과 안정 상태 분석이 있다. 안정 상태 분석에서는 시스템의 상태가 고장과 수리에 따라서 계속 변화해 가다가, 언젠가는 더 이상 변화지 않는 상태에 이르게 된다. 즉, 안정 상태에 도달했을 때 시스템이 각 상태에 머무를 확률이 안정 상태 확률이다. 시스템이 n개 상태로 구성되었을 때, 구하려는 각 상태의 안정 상태 확률을 나타내는 행렬을 P라고 하자.
| (7) |
이러한 안정 상태 확률은 그림 2와 같은 전이율 행렬에 미분 방정식을 적용해서 구할 수 있다(자세한 수학은 [8]를 참조하기 바람). 당연히, 각 상태의 안정 상태 확률을 모두 더하면 1이다.
| (8) |
Pi(t)를 특정 t 시점에 시스템이 상태 i에 머무를 확률이라고 하자. 그러면 시점 t에서 시스템의 고장율은 아래와 같다.
| (9) |
안전 기능의 평균 고장율을 구하는 식 (5)에 있는 식 (9)를 치환하면 다음을 얻는다.
| (10) |
식 (10)의 값은 마코프 모델에 있는 고장 상태의 안정 상태 확률을 모두 더한 값과 같다. 따라서 마코프 모델을 통한 안전 기능의 고장율은 다음과 같다.
| (11) |
3.2 확률 모델 검증을 이용한 SIL 검증
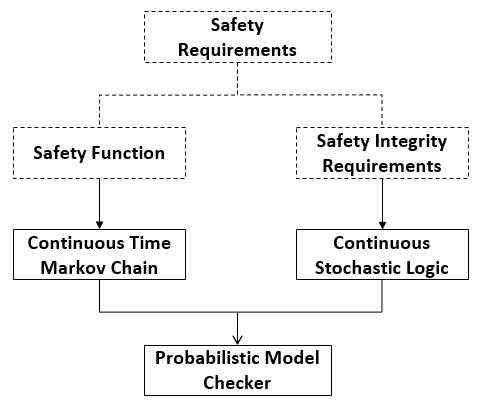
전 절에서는 마코프 모델이 안전 기능의 고장율을 계산하는데 사용될 수 있다는 이론적 근거를 설명하였다. 이것을 바탕으로 본 절에서는 확률 모델 검증을 이용하여 안전 기능의 SIL 검증을 그림 3과 같이 제안한다. 안전 기능은 연속 시간 마코프 체인 (CTMC, Continuous-Time Markov Chain)으로 표현하며, 안전 무결성 요구사항은 연속 확률 논리(CSL, Continuous Stochastic Logic)로 나타내며, 확률 모델 검증 도구는 PRISM(PRobabIliStic Model checker)을 사용한다[9].
SIL 검증에 사용될 모델 M은 연속 시간 마코프 체인이다.
| (12) |
여기서 S는 상태들의 집합이다. SIL 검증에서는 고장 상태 집합 D⊆S가 사용되며, 나머지 상태인 U=S-D는 정상으로서 D∩U=∅, D∪U=S이다. s0∈S는 시작 상태이다. R:S×S→ℝ≥0은 상태간의 전이를 나타낸다. SIL 검증에서는 고장 및 수리와 관련된 전이율을 각 전이에 할당한다. 전이율은 상수로서 양의 실수 값을 가지며, 지수 분포의 모수로 사용된다. L:S→2AP는 단순 명제를 각 상태에 배정하는 함수이다. SIL 검증에서의 단순 명제는 AP={up, down}이며, L(s∈D)={down}와 L(s∈U)={up}이다.
안전 기능에 대한 모델을 작성한 후에, 안전 무결성 요구사항인 위험 고장율과 관련된 속성을 연속 시제 논리로 기술한다. 속성 명세에 사용되는 연산자 P, S의미는 다음과 같다:
- - P는 마코프 모델의 행위를 일시적으로 관찰한 순간적 확률(Transient Probability) 이다.
- - S는 마코프 모델의 행위를 오랫동안 관찰한 안정 상태 확률(Steady State Probability)이다.
다양한 속성을 이용하여 SIL 검증을 수행할 수 있다. 예를 들어, 고장율이 SIL 2에 속함을 다음과 같은 속성으로 검증할 수 있다.
| (13) |
| (14) |
여기서 down은 전체 고장 상태이며, 물음표 ?의 의미는 안전 상태 확률을 묻는 질의이다. 주어진 안전 기능이 위의 두 속성을 만족하면 표 1에 따라서 SIL 2이다. 서브시스템별 고장율도 구할 수 있다.
| (15) |
여기서 FailSensor는 입력부의 고장 상태 집합이다. 서브시스템뿐만 아니라, 안전 기능의 전체 고장율도할 수 있다.
| (16) |
위의 식 (16)은 SIL 검증에 필수적으로 사용된다. 안정 상태 확률도 유용하지만, 특정 시간 구간에서 어떤 서브시스템이 고장에 더 취약한지 등을 분석할 수 있다.
| (17) |
즉, 입력부가 제일 먼저 고장을 일으킬 확률을 식 (17)을 이용하여 구할 수 있다. 이러한 분석을 통해서 안전 기능을 구성하는 서브시스템들을 고장율에 따라 중요도를 구분할 수 있다.
지금까지, 안전 기능의 고장 및 수리와 관련된 동적 행위를 연속 시간 마코프 체인으로 모델링하는 방법과 SIL 검증에 필요한 속성을 명세하는 방법을 살펴보았다. 이제, 확률 모델 검증 도구인 PRISM으로 SIL 검증을 수행할 수 있다.
Ⅳ. 실험 및 평가
본 논문에서 제안한 방법을 탱크 과류 방지(Tank Overfill Protection)에 적용하였다[10]. 위험요인은 탱크안으로 유입되는 것이 설정 수위 이상인 경우이다. 위험요인을 방지하는 안전 기능은 그림 4와 같다. 입력부는 센서를 이중화한 1oo2 (1-out-of-2) 구조이며, 제어부 역시 로직을 1oo2 구조로 이중화 하였고, 출력부만 단일 밸브를 사용하는 1oo1 구조이다. 안전 기능의 목표는 SIL 2라고 가정한다.
여기서는 이중화시 동일 컴포넌트가 사용된다고 가정한다. 이런 경우에, 컴포넌트가 동시에 모두 고장이 나서, 이중화 효과가 전혀 소용없는, 공통 원인 고장인 CCF(Common Cause Failure)를 고려해야 한다. CCF를 다루기 위해서 본 논문에서는 다음과 같은 β-요소 기법을 사용한다[9].
| (18) |
여기서 β는 CCF 고장율이다. 예로서, β=10% 의미는 전체 고장율 중에서 10%만 공통 원인 고장이며, 나머지 90%는 개별 컴포넌트 고장이다.
제안한 방법으로 안전 기능에 관한 SIL 검증을 수행하는 방법은 다음과 같다. 먼저, 센서를 이중화한 입력부의 마코프 모델은 그림 5와 같다. 10개의 상태 중에서 D={3,4,5}이다. 상태 0은 두 센서가 모두 정상이며, 상태 1~2에서는 센서 하나만 고장이다. 1oo2 구조라서 센서 하나만 고장 나더라도 이중화 덕분에 기능을 수행할 수 있다.
제어부는 로직 컴포넌트를 이중화한 1oo2 구조이기 때문에 입력부와 같은 마코프 모델을 사용하였고, 출력부는 단일 밸브를 사용하는 1oo1 구조라서 그림 2의 마코프 모델을 사용하였다.
마코프 모델을 작성한 후에 SIL과 관련된 다양한 속성을 검증하였다. 사용된 고장율은 [10] 데이터를 이용하였다. 식 (15), (16)을 이용하여 입력부 및 전체의 고장율 검증한 결과이다.
| (19) |
| (20) |
따라서 과류 방지를 수행하는 안전 기능은 SIL 2 임을 알 수 있었다. 이 속성을 검증하는데 소요된 시간은 0.007초였다.
확률 모델 검증으로 구한 값을 어떻게 믿을 수 있겠는가? 이 질문에 대답하기 위해서, IEC 61508문서의 계산 공식과 비교하였다. 입력부에 사용된 1oo2 구조에 관한 공식이다[1].
| (21) |
확률 모델 검증에 사용되었던 데이터를 똑 같이 사용하여 위의 공식을 풀면, 입력부의 고장율은 PFDsavg=1.10*10-5로서 모델 검증으로 구한 식 (19)의 값과 같다. 그 뿐만 아니라, IEC 61508 공식을 이용하여 구한 안전 기능의 전체 고장율과 확률 모델 검증으로 얻은 결과도 동일하였다.
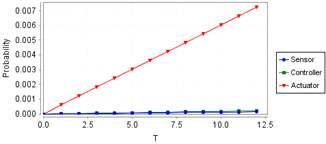
본 연구가 제공하는 이점은 다음과 같다. 첫째, IEC 61508에는 일부 구조에 대한 공식만 제공하고 있을 뿐이다. 만약 표준에 없는 구조를 사용하여 안전 기능을 설계하는 경우에 본 논문의 방법을 사용하면, 공식이 알려지지 않은 구조도 계산할 수 있을 것이다. 둘째, SIL 검증을 위해서 정적 모델이 아닌 동적 모델을 사용하였다. 따라서 정적 모델에서와 같이 고장율 값을 계산할 뿐만 아니라 시간 변화에 따른 고장율을 검증하거나 랜덤 시뮬레이션 할 수 있다. 탱크 과류 사례에서 고장율을 서브시스템 별로 구분하면 입력부 3%, 제어부 3%, 출력부 94% 이다. 그림 6에서 보듯이 시간 경과에 따라서 시스템 전체 고장율에 가장 영향을 미치는 것이 출력부임을 알 수 있다. 이러한 정보를 바탕으로 출력부의 고장율을 줄이기 위하여 유지보수 기간을 줄이거나, 또는 고장율이 더 낮은 컴포넌트로 교체하던가, 아니면 1oo1 구조 대신에 이중화 내지는 삼중화 구조를 사용할 수 있을 것이다.
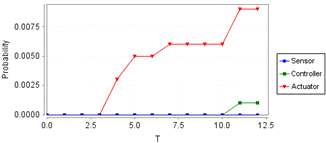
확률 모델 검증 결과는 이와 같은 의사 결정에 도움을 줄 수 있다. 또한 그림 7에서 보듯이 식 (17)을 이용하여 안전 기능을 1년 사용하는 경우를 가정해서 서브시스템을 랜덤 시뮬레이션한 결과, 출력부가 가장 일찍 고장을 일으키는 것으로 확인되었다.
Ⅴ. 결론 및 향후 과제
안전 기능은 위험요인으로부터 생명, 재산, 환경을 지키는 안전 보호 시스템이기 때문에, 위험요인이 발생하였을 때 고장 없이 정상 작동해서 주어진 임무를 수행해야 한다. SIL 검증은 안전 기능의 성능이 SIL을 만족하는지 확인하는 작업이다. 본 논문에서는 확률 모델 검증을 이용하여 정량적인 SIL 검증 방법을 제안하였다. 그리고 제안 방법의 유효성을 확인하기 위하여 탱크 과류를 방지하는 안전 기능 사례에 적용해 보았다. 그 결과 IEC 61508 공식과 같은 결과를 얻었다.
뿐만 아니라 SIL 정량적 검증을 위해서 기존에는 이진 정적 모델을 사용하였으나, 본 연구에서는 확률 동적 모델을 사용하였다. 동적 모델을 사용함으로서 안전 기능의 고장율 계산뿐만 아니라 시간의 흐름에 따른 시스템 행위도 분석할 수 있었다.
본 논문에서는 IEC 61508 낮은 요청 모드에서 사용되는 PFD만을 다루었으나, 향후에는 이러한 연구를 확장해서 IEC 61508 높은 요청 모드에서 사용되는 PFH 정량화도 수행할 것이다. 또한, 자동차 표준인 ISO 26262에서 사용되는 PMHF 정량화도 연구하고자 한다.
Acknowledgments
이 논문은 2016학년도 경기대학교 연구년 수혜로 연구되었음
References
- IEC, "IEC 61508:2010 Functional safety of electrical/electronic/programmable electronic safety-related systems", International Electrotechnical Commission, (2010).
- E. B. Abrahamsen, "A new approach of uncertainty treatment in the verification of safety integrity level of safety instrumented system", Master Thesis, University of Stavanger, (2015).
- IEC, "IEC 61078:2016 Reliability block diagrams", International Electrotechnical Commission, (2016).
- IEC, "IEC 61025:2006, Fault tree analysis", International Electrotechnical Commission, (2006).
- T. Grimm, D. Lettnin, and M. Hübner, "A Survey on Formal Verification Techniques for Safety-Critical Systems-on-Chip", Electronics, 7(81), p1-27, May), (2018.
- N. Das, and W. Taylor, "Quantified fault tree techniques for calculating hardware fault metrics according to ISO 26262", in Proc. of Product Compliance Engineering, IEEE Xplore, p1-8, May), (2016.
- IEC, "IEC 61165:2006 Application of Markov techniques", International Electrotechnical Commission, (2006).
-
M. Rausand, "Reliability of Safety-Critical Systems: Theory and Applications", Wiley Publishing, (2014).
[https://doi.org/10.1002/9781118776353]

- M. Kwiatkowska, G. Norman, and D. Parker, "PRISM 4.0: Verification of Probabilistic Real-time Systems", In Proc. of Computer Aided Verification (CAV'11), 6806, p585-591, Jul), (2011.
- Logic Solver for Tank Overfill Protection, http://www.miinet.com/Portals/0/PDFs/Logic_Solver_for_Tank_Overfill_Protection_White_Paper_Moore_Industries.pdf, . [accessed: Aug. 20, 2018]

1985년 2월 : 경기대학교 전자계산학과(이학사)
1987년 8월 : 중앙대학교 전자계산학과(이학석사)
1991년 2월 : 중앙대학교 전자계산학과(공학박사)
1991년 2월 ~ 현재 : 경기대학교 컴퓨터공학부 교수
1999년 ~ 2000년 : 미국 카네기멜론대학 전산학과 연구교수
2006년 ~ 2007년 : 미국 카네기멜론대학 전산학과 연구교수
2014년 ~ 2016년 : 한국정보과학회 소프트웨어공학 소사이어티 회장
관심분야 : 소프트웨어 공학, 정형 검증, 소프트웨어 안전성, 시스템 안전성 분석