단안 카메라 기반 3차원 물체 인식 기법 및 6축 머니퓰레이터 경로계획을 이용한 탁구 로봇의 구현

2.1 탁구 로봇의 구동 환경

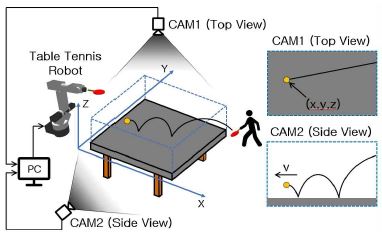
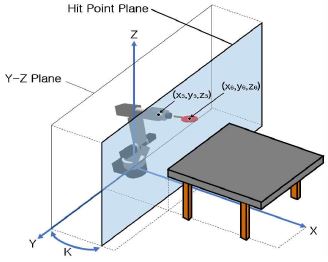
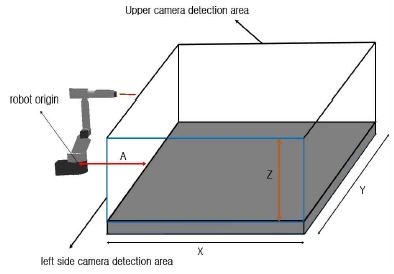
탁구 로봇의 구동 환경 요소는 그림 1과 같이 탁구대, 탁구공 타격을 위한 6축 다관절 로봇, 탁구공을 인식하기 위한 두 대의 단안 카메라, 그리고 영상처리 및 6축 로봇 구동을 위한 PC로 구성되어 있다. 그림 1에 나타낸 탁구대 상단에 설치된 단안 카메라(CAM1)는 탁구공의 좌표(x,y,z)를 검출하는데 사용되고, 탁구대 측면에 설치된 단안 카메라(CAM2)는 탁구공의 속도를 추적하는데 사용된다. PC는 CAM1과 CAM2의 영상을 수집하여 처리하고 머니퓰레이터에 구동 신호를 보낸다. 그리고 다관절 로봇의 말단장치(End-effector) 부분에는 탁구채를 고정하여 탁구 로봇의 구동 환경을 조성하였다.

Fig. 1.

Environment for the table tennis robot

2.2 탁구 로봇의 기구학적 해석

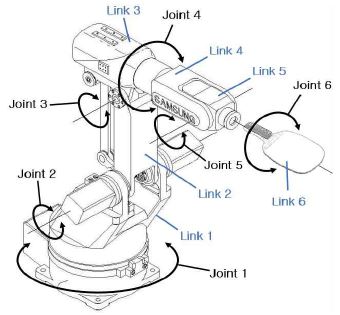
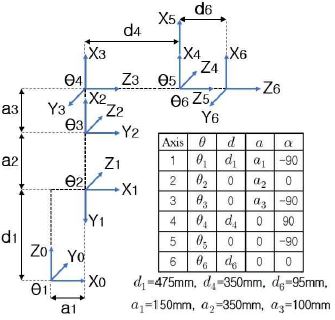
그림 2는 탁구 로봇으로 사용된 삼성 AS2 로봇(Samsung FARAMAN AS2 Robot)의 관절과 링크의 구성을 나타내며, 그림 3은 삼성 AS2 로봇의 정기구학(Forward Kinematic) 모델링을 위한 직각좌표계와 D-H(Denavit-Hartenberg) 변환 파라미터(Parameter)를 나타낸다[6].

Fig. 2.

Joints and links of Samsung AS2 robots

Fig. 3.

Coordinate frame system of the Samsung FARAMAN AS2 robot and D-H parameters

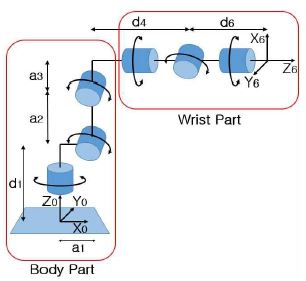
그림 4는 역기구학(Inverse Kinematics)을 해석하기 위해 기구학적 분리(Kinematics Decoupling)기법을 사용하여 다관절 로봇을 몸통 부분과 손목 부분으로 분리한 것을 나타낸다[6].

Fig. 4.

Body part and wrist part through kinematic decoupling

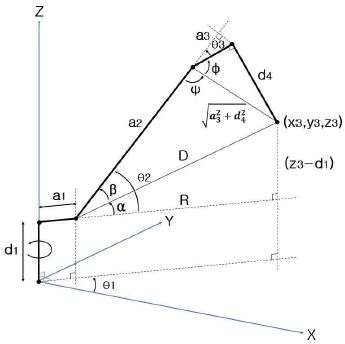
그림 5는 3차원 공간인 xyz 좌표계에서 몸통 부분의 관절(Joint) 및 링크(Link)를 나타낸다. 몸통 부분의 끝 좌표(x₃,y₃,z₃)가 주어지면 역기구학을 사용하여 관절 a₁~a₃에 대한 θ₁,θ₂,θ₃값들의 해는 식 (1)~(3)에 의해 결정된다[6].

Fig. 5.

Diagram for joint a1 to a3 of body point

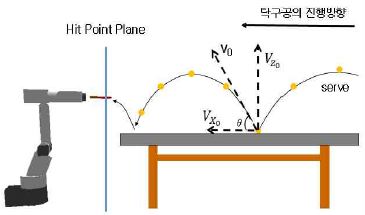
탁구공 타격을 위한 말단장치의 역기구학 해석 과정에서 손목 부분의 관절 a₄~a₆인 θ₄,θ₅,θ₆값들에 대한 무수히 많은 해가 존재한다. 본 논문에서는 이러한 문제점을 해결하기 위해 탁구공 타격이 이루어지는 평면을 타격 평면(Hit Point Plane)으로 정의하였다. 타격 평면은 그림 6과 같이 yz 평면이 X축 방향으로 일정한 거리(K) 간격에 위치한 평면으로 정의된다. 탁구 로봇이 탁구공 타격 시 몸통 부분의 끝 좌표(x₃,y₃,z₃)와 말단장치의 좌표(x₆,y₆,z₆)는 항상 타격 평면상에 위치하도록 하며 θ₄값의 해는 식 (4)에 의해 결정되고, θ₅,θ₆값의 해는 z₃ ≥ z₅경우 식 (5)에 의해, z₃ ≥ z₆경우 식 (6)에 의해 결정된다.

Fig. 6.

Hit point plane with a distance K from the robot

2.3 탁구 로봇의 경로계획

탁구공 타격을 위해 타격 평면상에 두 좌표(x₃,y₃,z₃)와 (x₆,y₆,z₆)를 제약하더라도 평면상에 무수히 많은 해가 존재하게 된다.

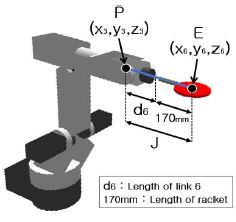
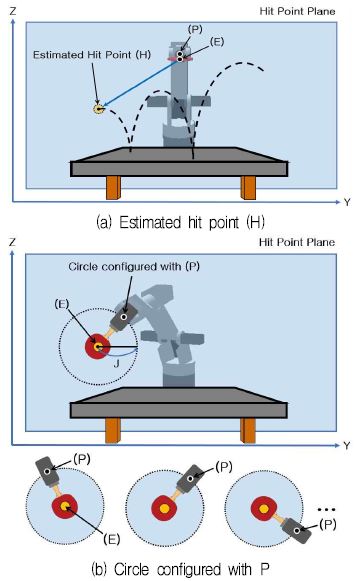
이러한 문제를 해결하기 위해 본 논문에서는 탁구 로봇의 최단 경로를 계산하여 각 관절이 최소한의 움직임으로 예측타격지점(Estimated Hit Point)까지 도달할 수 있는 경로계획 기법을 제안한다. 그림 7은 몸통 부분의 끝 좌표(P) 및 말단장치의 좌표(E) 위치, 그리고 좌표 P와 좌표 E 사이의 거리 간격(J)를 나타낸다. 그림 8(a)는 탁구공의 예측 궤적 및 탁구공이 타격 평면상에 위치할 예측타격지점(H)를 나타내며, 좌표 E가 H에 도달함으로써 로봇이 탁구공 타격 자세를 갖추게 된다. 좌표 E가 H에 도달한 이후의 그림 8(b)에서는 원 중심이 좌표 E가 되고 반지름 길이가 J인 원을 타격 평면상에 나타내며, 이 원의 둘레는 좌표 P가 위치할 수 있는 무수히 많은 해를 나타낸다.

Fig. 7.

Position of coordinate P and E, interval J of them

Fig. 8.

Estimated hit point H and circle configured with P

본 논문에서는 탁구채인 말단장치가 예측타격지점 H에 위치하기 위한 최소 관절 변화량 탐색 기반 경로계획 기법을 제안한다. 경로계획의 첫 번째 단계로 그림 8과 같이 타격 평면상의 예측타격지점 H에 말단장치의 좌표 E가 위치하여 원의 중심으로 하고 반지름 길이가 J인 원을 구성한다. 두 번째 단계로는 원의 둘레의 모든 해에 대해 2.2절의 역기구학을 통해 모든 관절 θ₁,θ₂,θ₃,θ₄,θ₅,θ₆값의 해를 계산하여 도출한다. 세 번째 단계는 (최적 좌표 P를 지정하기 위해) 현재 상태의 로봇 관절 (θ_p1,θ_p2,θ_p3,θ_p4,θ_p5,θ_p6) 값과 도출된 관절 (θ₁,θ₂,θ₃,θ₄,θ₅,θ₆) 값의 차를 제곱하여 누적한다. 누적된 모든 경우의 값들을 비교하여 가장 최솟값이 되는 지점을 도출하고 이 지점을 좌표 P로 지정한다. 이로써 무수히 많은 해 중 로봇의 모든 관절 변화량이 최소가 되도록 하는 몸통 부분의 끝 좌표 P의 해를 탐색하였다.

3.1 탁구공의 좌표 검출

CAM1은 탁구공의 좌표검출을 위해 탁구대 상단에 설치되며 전체 탁구대의 xy 좌표평면을 촬영한다. 탁구공의 정확한 좌표 검출을 위해서는 카메라의 화각을 고려한 카메라 최소높이를 설정하고 단안 카메라에 의한 탁구공 위치 좌표 오차를 보정하는 기법을 사용한다. 이를 통해 최종적으로 검출된 좌표를 실제 3차원 공간의 좌표로 변환하여 로봇의 구동이 이루어진다.

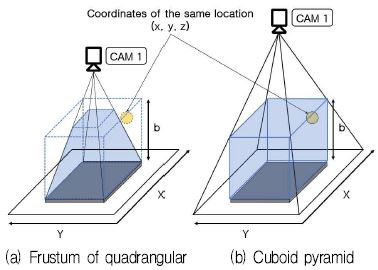
그림 9(a)와 같이 CAM1의 화면에 탁구대만 나오도록 카메라 높이를 설정하여 촬영할 경우 탁구대 영역 안에서 공이 일정 높이 이상으로 떠오르면 카메라 화각에 의해 인식범위를 벗어나 탁구공이 검출되지 않는 현상이 발생한다. 본 논문에서는 이러한 문제를 해결하기 위해 그림 9(b)와 같이 로봇이 타격 가능한 직육면체 영역을 모두 인식하는 카메라의 최소높이 설정방법을 제안한다.

Fig. 9.

Ball recognition space according to installation height of camera

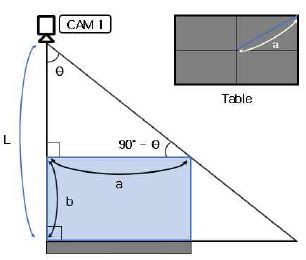
그림 10은 CAM1의 최소높이 설정에 필요한 로봇팔의 최대 구동 높이(b), 탁구대의 중심에서 대각선 끝점까지 거리(a), 카메라 화각(2θ)을 표현하였고 본 논문에서 제안하는 탁구공의 위치 인식을 위한 카메라의 높이는 식 (7)을 통해 구할 수 있다.

Fig. 10.

Setting the camera minimum height

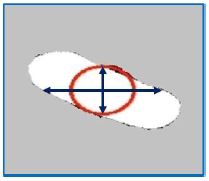
탁구공의 정확한 좌표를 검출하기 위해 그림 11과 같이 단안 카메라 CAM1이 촬영한 화면에서 탁구공을 관심영역으로 지정하여 이진화를 수행하였으며, 잔상에서 탁구공의 정확한 중심점 검출을 위해 잔상의 중심점에서 상 하 좌우 탐색을 통해 원을 검출하였다.

Fig. 11.

Binarization and detection for the ball

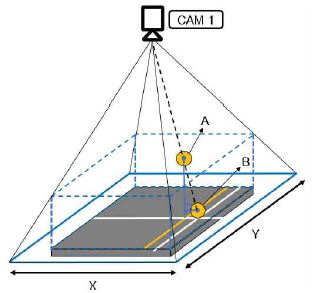
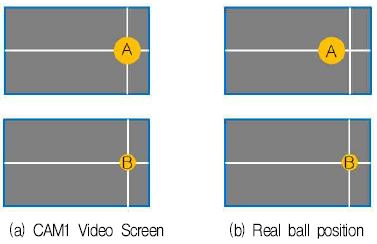
본 논문에서는 단안 카메라 한 대만을 사용하여 탁구공의 좌표를 검출한다. 좌표를 검출함에 있어서, 그림 12와 같이 카메라를 중심으로 동일한 직선상에 탁구공 A, B가 위치할 경우 탁구공 A, B의 3차원상의 실제 좌표는 다르다. 그림 13(a)의 카메라 영상에서 검출되는 탁구공 A, B의 중심 좌표가 같아지는 현상이 발생한다. 따라서 그림 13(b)와 같이 영상 좌표계에서 인식된 탁구공의 좌표 정보와 탁구공의 크기 정보를 이용하여 실제 좌표계상의 좌표로 변환해 주는 과정이 필요하다. 좌표 변환을 위해서는 탁구공의 크기 정보를 픽셀(Pixel) 기반으로 양자화 하여 도출된 카메라와 탁구공 사이의 거리 값과 영상에서 검출되는 탁구공 중심점 좌표에서 영상화면 중심까지의 거리 값이 필요하며, 이를 이용해 탁구공 실제 좌표를 보정하는 기법을 제안한다.

Fig. 12.

Position of the ball in xy coordinate plane captured by CAM1

Fig. 13.

Difference of actual xy coordinate of the ball according to the ball size

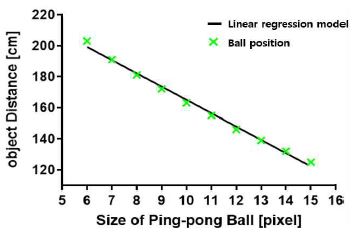
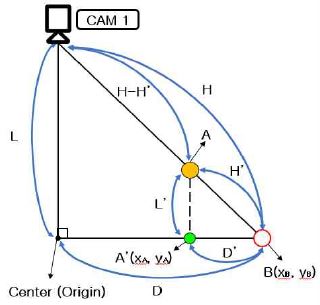
탁구공의 중심좌표를 보정하기 위해 카메라와 탁구공 사이의 실제 거리(H-H^')를 측정하여 표본화하고, 표본화 단계에서 사용된 표본의 개수는 로봇팔의 최대 구동 높이를 고려하여 그림 14와 같이 10개로 결정하였다. 이 표본들을 이용하여 단위픽셀마다 변화하는 카메라와 탁구공 간의 거리를 식 (8)의 선형 회귀 분석을 통하여 직선 방정식인 식 (9)와 같이 도출한다[7].

Fig. 14.

Distance between camera and ball according to pixel change

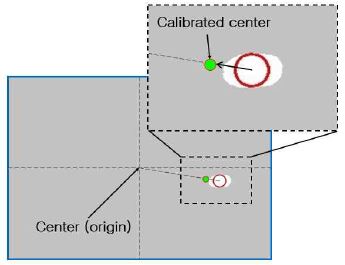
그림 15의 영상화면 중심점에서 탁구공 중심점까지 거리 D는 실제 좌표계 길이로 계산되기 때문에 CAM1이 촬영하는 실제 좌표계의 길이와 화면 해상도 사이의 비율을 이용하여 식 (10)와 같이 계산한다. 위의 값들을 중심점 좌표 보정을 위해 삼각비로 계산하면 영상화면에 나타나는 B좌표와 보정하여 검출할 A^'좌표까지의 거리 D^'가 계산된다. 이 거리 값을 이용하여 식 (11) 및 (12)와 같이 좌표를 보정하고, 보정된 좌표는 그림 16과 같이 영상 화면에 점으로 표시된다.

Fig. 15.

Searching method for real ball coordinate through ball position coordinate calibration

Fig. 16.

Center of calibrated ball

CAM1 및 CAM2의 영상에서 탁구공의 정확한 위치를 검출한 이후에는 로봇 구동을 위해 그림 17과 같은 3차원 공간상의 실제 좌표로 변환해야 한다. 식 (13)은 CAM1의 영상에서 검출된 좌표 pixel X, pixel Y와 카메라가 촬영하는 영역의 실제 길이 X, Y 사이의 비율을 이용한 좌표변환을 나타낸다. 식 (14)는 CAM2의 영상에서 검출된 좌표pixel X와 실제 길이 X사이의 비율을 이용한 좌표변환을 나타내며, CAM2는 측면 카메라이기 때문에 X축 좌표 정보만 고려한다. 공통적으로 X축의 경우 로봇의 원점을 기준으로 타격 평면을 설정하기 때문에 로봇 원점에서 최초로 카메라에 인식되는 실제 X좌표까지의 거리 A를 합산하여 로봇 구동을 위한 실제 좌표 real X pos, real Y pos로 변환한다.

Fig. 17.

Real 3D coordinate system for the table tennis robot

3.2 탁구공 타격지점 예측

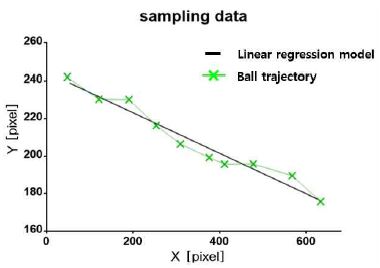
그림 18은 CAM1의 화면에서 탁구공의 중심점 좌표를 각각의 프레임마다 검출하여 표본화한 것이다. 타격지점의 정확한 Y좌표를 검출하기 위해 식 (8)과 같이 표본들의 거리오차 합(SSE, Error Sum of Squares)이 최소가 되는 선형 회귀 분석을 이용해 그림 19와 같이 검출한 표본들을 탁구공의 궤적에 대한 직선 방정식으로 도출한다[7].

Fig. 18.

Sampling the ball center coordinates in xy coordinates of CAM1

Fig. 19.

Linear regression using center coordinate samples

그림 20과 같이 좌측에 설치된 CAM2는 탁구공의 속도를 추적하여 로봇의 타격 시점을 결정한다. CAM2에서 추적한 탁구공의 속도를 이용하여 식 (15)와 (16)과 같이 탁구공의 X축 방향 속도 및 수평 이동 거리를 계산하고 타격지점에 도달하는 시점을 예측하여 로봇을 구동한다.

Fig. 20.

Calculation for ball speed and hit point

4.1 성능 평가 실험방법

본 논문에서는 해상도 640×480, 11fps인 단안 카메라의 영상을 받아 Intel Core i5-6600 CPU 기반 PC의 MFC 환경에서 OpenCV를 사용하여 탁구 로봇을 구현하였다. 탁구로봇의 타격률을 측정하기 위해 탁구공 타격 성공에 대한 요구조건을 정의하였으며 탁구공이 타격지점으로 이동한 후 머니퓰레이터의 말단장치에 부착된 탁구채가 탁구공을 타격한 경우를 ‘타격에 성공하였다’라고 정의한다.

표 1의 Case 1은 카메라 최소 높이를 그림 9(a)와 같이 사각뿔대 영역만을 인식하도록 설치하고 탁구공의 위치 좌표를 보정하지 않은 타격률 실험 결과를 나타내고, Case 2는 카메라 최소 높이를 그림 9(b)와 같이 본 논문에서 제안한 카메라 최소 높이 설정하고 탁구공의 위치 좌표에 대해 보정한 타격률 실험 결과를 나타낸다. 한 세트를 탁구공 10개로 기준을 잡고 각각의 Case마다 10세트를 시행하여 총 100회 탁구공을 던져 표본을 기록하고 타격률을 측정하였다.

4.2 실험 결과 및 분석

타격률 실험을 진행한 결과, 표 1의 Case 1과 같이 탁구공의 위치 좌표 보정 등 보정 시스템이 없는 타격률 실험에서 평균 10%의 타격률을 확인하였고, Case 2와 같이 본 논문에서 제안된 탁구공의 위치 좌표 보정 등 보정 시스템이 있는 타격률 실험에서는 평균 50%의 타격률로 증가된 것을 확인할 수 있었다[8].

Table 1.

Hit rate before and after ball position coordinate calibration system

본 논문에서 제안된 알고리즘들을 적용한 탁구 로봇의 평균 타격률이 50%에 미치는 이유는 카메라 영상처리 시 고속으로 이동하는 물체의 잔상이 영상에 투영되는 문제가 발생하고, 해상도 640×480에서 반지름 20mm인 탁구공 크기를 이용해 카메라와 물체 사이 거리 값을 양자화(Quantization)할 때 픽셀 간의 양자화 단위가 약 9cm로 실제 위치 좌표에 대한 양자화 오차 문제로 분석된다.