파형 구조와 공진주파수 및 세 가지 특성벡터 융합 기법의 레이더 표적 구분 성능 분석
초록
본 논문에서는 총 6가지의 특성벡터 추출 기법(파형 구조, EP 기반 CLEAN 기법으로 추출한 공진주파수, Prony 기법으로 추출한 공진주파수, 파형구조와 EP 기반 CLEAN 기법의 융합, 파형구조와 Prony 기법의 융합, 파형구조와 EP 기반 CLEAN 기법 및 Prony 기법의 융합)들에 대한 레이더 표적 구분 성능을 비교 분석하였다. 표적 구분에 사용된 표적은 4개의 서로 다른 항공기 표적이며 3D 캐드 모델과 FEKO 툴을 이용하여 RCS 데이터를 획득하였다. 표적 구분 실험을 위한 구분기로는 MLP(Multi-Layered Perceptron) 신경망을 이용하였으며, 신뢰도 확보를 위해 100회의 몬테카를로 시뮬레이션을 수행하였다. 실험 결과 파형구조 특성벡터와 EP 기반 CLEAN 기법 및 Prony 기법으로 추출한 공진 주파수 특성벡터들을 모두 융합한 경우에 가장 좋은 성능을 가짐을 확인할 수 있었다.
Abstract
In this paper, we analyzed and compared the performance of radar target classification for the six feature vector sets such as waveform structure, complex natural resonance(CNR) frequency using evolutionary programming (EP)-based CLEAN, CNR frequency using Prony’s method, fusion of waveform structure and EP-based CLEAN, fusion of waveform structure and Prony’s method and fusion of waveform structure, EP-based CLEAN and Prony’s method. Four aircraft targets are used for the target classification. Monostatic radar cross section (RCS) of four targets is obtained using the 3D CAD models and FEKO simulation tools. The MLP neural network is used as classifier and 100 Monte carlo simulations are performed for the reliability of the results. The results show that the fusion of waveform structure, EP-based CLEAN and Prony’s method has the best performance among six feature vector sets.
Keywords:
radar target classification, feature vector, waveform sturucture, complex natural resonance frequencyⅠ. 서론
레이더 신호는 표적에 대한 정보를 포함하고 있으므로 이러한 정보를 신호처리를 통하여 추출하고 이를 이용하여 표적을 인식하는 기술을 비협조적 표적인식 기법(NCTR, Non-Cooperative Target Recognition) 라 한다. 레이더 표적 인식을 위한 특성벡터로는 초기 시간 영역에서 관찰할 수 있는 산란점(Scattering Center)과 후기 시간 영역에서 관찰되는 복소 고유 공진(CNR, Complex Natural Resonance) 주파수가 있다[1]. 초기 시간의 산란점은 주로 높은 주파수에서 발생하는 산란 현상이며 넓은 대역폭을 사용할 경우에 관찰이 가능하며, 후기 시간의 CNR 주파수는 낮은 주파수 대역에서 관찰되는 현상이다. 본 논문에서는 주로 저 RCS 표적(미사일, 스텔스표적 등)을 탐지하기 위해 사용되는 HF 대역 레이더에 초점을 맞춘다[2]. HF 레이더는 매우 낮은 주파수 대역을 사용하므로 공진현상을 관찰할 때는 유리하지만 대역폭을 넓게 확보할 수 없어 산란점을 관찰하기에는 부적절하다. 따라서 이런 경우에는 초기 시간 영역에서 산란점 대신에 다른 특성 벡터를 이용해야하는데 본 연구에서는 파형 구조로부터 직접 특성벡터를 추출하는 방식을 사용하였다[3]. 후기 시간 영역에서는 HF 레이더가 충분히 낮은 대역이고 표적의 물리적인 크기 또한 공진 현상을 관찰하기에 적절하므로 복소 고유 공진 주파수를 추출하여 특성벡터로 이용하였다[4]. 공진 주파수를 추출하는 기법에는 여러 다양한 기법들이 있지만 본 논문에서 사용한 방법은 진화 프로그래밍(EP, Evolutionary Programming) 기반의 CLEAN 기법[5]과 주파수 영역 Prony 기법[6]-[9]을 이용하였다.
이러한 기존의 연구에서 더 나아가 최근에는 표적인식 성능을 향상시키기 위해서 초기 시간과 후기 시간의 특성벡터를 융합하는 기법들에 대한 다양한 연구가 진행되고 있다[10]. 본 연구에서는 세 가지 융합 기법(파형구조와 EP 기반 CLEAN 기법의 융합, 파형구조와 Prony 기법의 융합, 파형구조와 EP 기반 CLEAN 기법 및 Prony 기법의 융합)을 새롭게 제시하고 성능을 분석하였다.
따라서 본 논문에서는 융합하기 전의 특성 벡터 세 가지(파형 구조, EP 기반 CLEAN 기법으로 추출한 공진주파수, Prony 기법으로 추출한 공진주파수)와 융합으로 얻어진 특성벡터 세 가지를 합하여 총 여섯 가지의 특성벡터에 대해 표적인식 성능을 비교 분석하였다. 실험 결과 파형구조와 EP 기반 CLEAN 기법 및 Prony 기법을 모두 융합한 특성 벡터가 가장 좋은 성능을 가짐을 알 수 있었다.
Ⅱ. 본론
2.1 특성벡터 추출 기법
본 논문에 사용된 특성 벡터 추출 방법으로는 파형 구조로부터의 특성 벡터 추출, 후기 EP 기반의 CLEAN 알고리즘, 그리고 피팅 오차를 이용한 여러 주파수 응답 샘플 집합으로부터 Prony 기법을 이용한 공진주파수 추출 방법이 사용되었다.
먼저 파형 구조로부터 표적 구분을 위한 특성 벡터를 추출하는 방법은 참고문헌 [3]에서 제안된 방법으로 파형의 모형에 대해 정확한 정의가 필요하지 않다는 장점을 가지고 있다.
참고문헌 [3]에서는 사용한 표적의 크기가 매우 작아 초기 시간 영역 응답을 관찰할 수 없는 환경에서 후기 시간 영역 응답의 파형 구조로부터의 특성 벡터추출 방법이 제시되었다. 하지만, 본 논문에서는 레이더 신호가 표적을 완전히 통과하기 이전의 시간인 초기 시간 영역 응답에 기반 하여 파형 구조로부터 표적의 특성 벡터를 추출하였다.
본 논문에서는 초기 시간 영역 신호의 파형에서 최대값과 최소값 사이의 시간 간격(Δt1) 및 크기 간격(Δa1)과 최대값과 두 번째 피크 값 사이의 시간 간격(Δt2) 및 크기 간격(Δa2)을 특성 벡터로 사용하였으며, 파형 구조로부터 추출된 특성 벡터 fWF는 다음의 식 (1)과 같이 표현할 수 있다[10].
| (1) |
다음으로 후기 시간영역 신호로부터 복소 고유 공진 주파수를 추출하였다. 일반적으로 레이더 신호의 후기 시간 영역 응답은 SEM(Singularity Expansion Method)에 의하여 식 (2)와 같이 표현된다[10].
| (2) |
여기서, sm = σm + jωm은 m번째 복소 고유 공진 주파수를 의미하며, am 및 Φm은 각각 m번째 공진주파수의 진폭과 위상을 의미한다. TL은 후기 시간 영역 응답이 시작하는 시간이며, TF는 후기 시간 영역 응답이 끝나는 시간을 의미하며, M은 후기 시간 응답에서의 공진주파수의 개수를 의미한다. 후기 시간 EP 기반의 CLEAN 알고리즘은 잡음에 강건하고, 모델 차수 추정에 둔감하며, 초기 추정이 필요 없다는 장점을 가지고 있지만 계산 속도가 오래 걸린다는 단점이 있다. 알고리즘에 대한 자세한 설명은 참고문헌 [5]에 잘 기술되어 있으므로 본 논문에서는 생략하도록 한다.
마지막으로 Prony 기법은 공진주파수 추출에 있어 계산 속도가 빠르고 초기 추정이 필요 없다는 장점을 가지고 있지만 다른 추출 기법에 비해 잡음에 민감하다는 단점이 있다. 피팅 오차를 이용한 여러 주파수 응답 샘플 집합으로부터의 Prony 기법을 이용한 공진주파수 추출 방법은 주파수 영역에서의 공진주파수 추출을 위한 방법이다. 먼저 주파수 샘플 개수에 따른 공진주파수 집합들을 추출한 후, 각 공진주파수 집합의 정확성을 계산하여 가장 정확한 공진주파수 집합을 결정한다. 이를 위해 주파수 응답으로부터 주파수 영역 샘플링 간격을 바꿈으로써 여러 주파수 응답 샘플 집합들을 구한다. 각각의 주파수 응답 샘플 집합으로부터 주파수 영역 Prony 기법을 이용하여 공진주파수 집합을 구하고, 구해진 공진주파수 집합들로부터 피팅 오차를 계산하여 가장 정확한 공진주파수 집합을 선택하는 방법으로 구체적인 절차는 참고문헌 [9]에 자세히 기술되어 있으므로 앞에서와 마찬가지로 본 논문에서는 생략하도록 한다.
2.2 특성 벡터 융합 기법
2.2절에서는 본 논문에서 사용된 공진주파수와 파형 구조 기반의 특성 벡터 융합 방법에 대하여 기술하도록 한다.
본 논문에서 제안하는 특성 벡터 융합 기법은 먼저 획득된 RCS 데이터로부터 IFFT(Inverse Fast Fourier Transform)를 이용하여 시간 영역 신호를 생성한 후, 생성된 시간 영역 신호를 초기 시간 영역과 후기 시간 영역으로 나눈다. 초기 시간 영역에서는 파형 구조로부터 표적의 특성 벡터를 추출하고, 후기 시간 영역에서는 EP 기반의 CLEAN 알고리즘 및 주파수 영역 Prony 기법을 이용하여 특성 벡터인 공진주파수를 추출한다. 복잡한 표적의 경우, 표적에 대해 정확한 공진주파수는 알 수 없지만 여러 개의 공진주파수가 존재할 수 있다. 동일한 레이더 신호로부터 추출된 특성 벡터라도 사용된 추출 기법에 따라 다른 값들이 추출될 수 있기 때문에 본 연구에서는 공진주파수 추출 기법들로부터 추출된 특성 벡터들을 융합함으로써 표적에 대한 정보를 더욱 증가시켜 표적 구분 실험을 수행하였다. 다음으로 각각 추출된 특성 벡터를 이용하여 융합된 특성 벡터(Combined Feature Vector)를 생성함으로써, 표적 구분 시에 초기 시간 및 후기 시간 영역의 정보를 모두 고려할 수 있다. 최종적으로, 위와 같이 융합된 특성 벡터를 이용하여 구분기를 통하여 표적 구분 실험을 수행하게 된다.
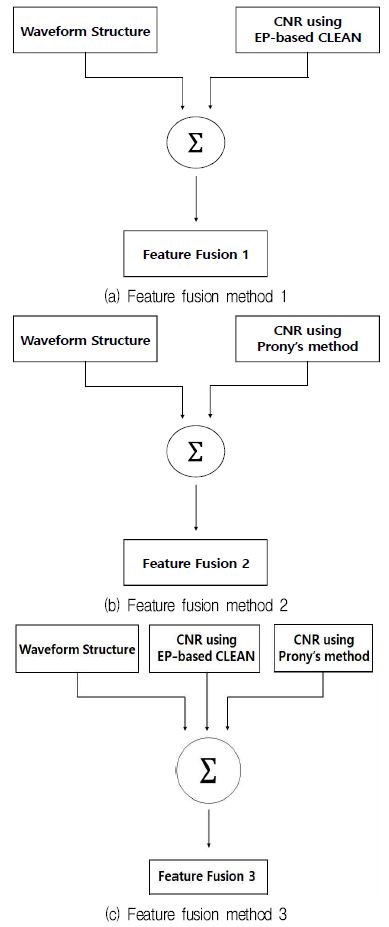
본 논문에서는 그림 1과 같이 세 가지 경우에 대하여 융합 특성 벡터를 생성하였다. 먼저 파형 구조로부터의 특성 벡터와 EP 기반의 CLEAN을 이용하여 추출된 특성 벡터를 융합한 경우(Feature Fusion 1), 파형 구조로부터의 특성 벡터와 Prony 기법을 이용하여 추출된 특성 벡터를 융합한 경우(Feature Fusion 2), 그리고 파형 구조로부터의 특성 벡터, EP 기반의 CLEAN을 이용하여 추출된 특성 벡터, Prony 기법을 이용하여 추출된 특성 벡터를 모두 융합한 경우(Feature Fusion 3)이다. 이와 같이 융합된 특성 벡터는 다음의 식 (3)∼(5)와 같이 표현될 수 있다.
| (3) |
| (4) |
| (5) |
여기서 ffusion1 ~ ffusion3는 융합된 특성 벡터를 의미한다. 또한, fEP는 후기 시간 EP 기반의 CLEAN 알고리즘을 이용하여 추출된 특성 벡터, fProny는 Prony 기법을 이용하여 추출된 특성 벡터를 의미하며, 각각 식 (6) 및 식 (7)과 같이 표현할 수 있다.
| (6) |
| (7) |
여기서 σEP1, σEP2, ωEP1, ωEP2는 EP 기반의 CLEAN 알고리즘을 이용하여 추출된 공진주파수를 의미하며 σProny1, σProny2, ωProny1, ωProny2는 Prony 기법을 이용하여 추출된 공진주파수를 의미한다.
Ⅲ. 시뮬레이션 결과
앞에서 설명한 여섯 가지 특성벡터들의 표적구분 성능을 검증하기 위해서는 먼저 표적의 RCS 데이터를 획득하여야 한다. 본 논문에서는 먼저 독일의 Altair 사에서 개발한 FEKO를 이용하여 표적들의 RCS를 획득하였다. FEKO는 EM 해석 시뮬레이션 툴 중 하나로서, RCS 계산 및 데이터베이스 구축을 위해 많이 사용되고 있다[4][11]. RCS 계산에 사용된 표적은 실제 크기와 흡사한 캐드 모델(CAD Model)이며, 이는 플라스틱 스케일 모델에 대해 3-D 스캐닝 및 모델링 과정을 통하여 3-D 캐드 모델을 얻은 후, 이를 스케일 업(Scale Up) 시켜줌으로써 획득할 수 있다[4]. 실험에 사용된 네 가지 표적(F-15, B-58, F-22, B-2)에 대한 실제 모양은 참고문헌 [11]과 [12]에 제시되어 있으므로 본 논문에서는 다시 제시하지 않도록 한다. 모노스태틱 RCS 계산 시, 해석 기법은 저주파 해석 기법인 MoM(Moment of Method)를 이용하였다. 주파수 범위는 표적의 물리적인 크기에 의한 공진주파수를 관찰할 수 있도록 0.2MHz에서 0.2MHz 간격으로 28MHz까지 140포인트로 계산하였으며, 편파각(Polarization Angle)은 90°로서, HH(Horizontally transmitting, Horizontally receiving) 편파만을 고려하였다. 또한, 표적의 모노스태틱 RCS는 좌우대칭이라는 점을 고려하여 표적의 측면각은 표적의 머리 부분을 0°로 봤을 때, 0°부터 180°까지 1° 간격으로 181개의 각도에서 계산하였다.
이렇게 획득된 레이더 신호로부터 먼저 초기 시간 영역 신호를 이용하여 파형 구조 기반의 특성벡터를 추출하였다. 표 1은 2.1절에서 설명한 파형구조로부터 추출한 네 가지 표적에 대한 특성 벡터를 보여주고 있다.
다음으로는 후기 시간 영역 응답의 특성 벡터인 공진주파수를 추출하기 위하여 EP 기반의 CLEAN 알고리즘과 Prony 기법을 이용하였다. 표적에 대한 정확한 공진주파수의 개수를 알 수 없기 때문에 본 논문에서는 EP 기반의 CLEAN 알고리즘 및 Prony 기법을 이용한 공진주파수 추출 시 공진주파수의 개수를 2개로 설정하여 각각의 표적마다 공진주파수를 추출하였다.
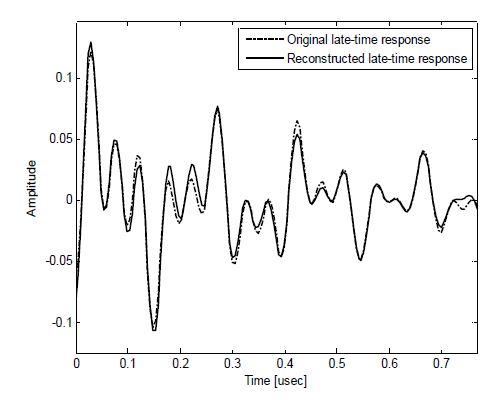
그림 2는 B-58 표적에 대한 원래의 후기 시간 영역 신호와 EP 기반의 CLEAN 알고리즘을 이용하여 추출된 복소 고유 공진 주파수에 의해 복원된 신호를 비교한 그림이다.
그림 2를 보면 원래의 후기 시간 영역 신호와 추출된 파라미터를 이용하여 복원된 신호가 거의 비슷한 것을 확인할 수 있다. 즉, 본 논문에서 사용된 알고리즘으로 추출된 고유 주파수 정보가 매우 정확함을 알 수 있다.
표 2는 앞에서 설명한 여섯 개의 특성벡터들에 대한 소수점 둘째자리에서 절사한 표적 구분 성능을 비교한 표이다. 구분기로는 MLP 신경망을 이용하였으며, 참고문헌 [10]에서 정의한 바와 같이 AWGN(Additive White Gaussian Noise)를 첨가한 후, 각 SNR(Signal to Noise Ratio)에서 100회의 몬테카를로 시뮬레이션을 수행하여 표적구분 확률에 대한 평균과 표준편차를 계산하였다. 실험 결과, 공진주파수만을 특성 벡터로 이용한 표적 구분 실험 결과, SNR이 40dB일 때를 제외하고 EP 기반의 CLEAN 알고리즘(방법2)를 이용했을 때가 Prony 기법(방법3)을 이용했을 때보다 더 좋은 표적 구분 성능을 갖는 것을 확인할 수 있다. 또한, 낮은 SNR(20dB 이하)에서는 파형 구조로부터 추출된 특성 벡터(방법1)을 이용했을 때가 공진주파수를 특성 벡터로 이용했을 때(방법2, 방법3)보다 표적 구분 성능이 더 우수하며, 높은 SNR(25dB 이상)에서는 EP 기반의 CLEAN 알고리즘을 이용하여 추출된 공진주파수를 이용했을 때(방법2)의 표적 구분 성능이 우수함을 보이고 있다.
특성 벡터 융합을 이용한 표적 구분 실험 시, 파형 구조로부터의 특성 벡터 추출 방법과 EP 기반의 CLEAN 알고리즘을 융합한 경우(방법4), 단순히 공진주파수만을 특성 벡터로 이용했을 때(방법2, 방법3)보다 표적 구분 성능을 향상시키는 것을 확인할 수 있다. 그리고 파형 구조로부터의 특성 벡터 추출 방법과 Prony 기법을 융합한 경우(방법 5)에는 Prony 기법만을 이용했을 때(방법 3)보다 표적 구분 성능을 향상시킬 수 있는 것을 확인할 수 있다. 마지막으로 세 가지의 특성 벡터를 모두 융합한 경우(방법 6)에는 특성 벡터 융합을 이용하지 않았을 때(방법 1, 2, 3)보다 SNR 15dB 이상에서 더 좋은 표적 구분 성능을 갖는 것을 확인할 수 있다. 결과적으로 공진주파수 및 파형 구조 기반의 특성 벡터 융합 방법이 SNR 25dB 이상에서 각각의 특성 벡터를 따로 사용했을 때보다 표적 구분 성능이 더 우수함을 확인할 수 있다.
Ⅳ. 결론
본 논문에서는 저주파 대역의 저해상도 레이더에 적용 가능한 여섯 가지의 특성벡터 추출 기법들에 대하여 표적 구분 성능을 비교 분석하여 가장 뛰어난 성능을 가지는 특성 벡터의 조합을 찾아내는 연구를 진행하였다. 여섯 개의 특성벡터는 파형 구조로부터 추출한 특성벡터(방법 1), EP 기반 CLEAN 기법으로 추출한 공진주파수(방법 2), Prony 기법으로 추출한 공진주파수(방법 3), 파형구조와 EP 기반 CLEAN 기법의 융합(방법 4), 파형구조와 Prony 기법의 융합(방법 5), 파형구조와 EP 기반 CLEAN 기법 및 Prony 기법의 융합(방법 6)이며 이중에서 방법 6이 가장 뛰어난 성능을 가짐을 확인할 수 있었다. 하지만, 방법 6은 좋은 성능을 가지는 반면 그 만큼 많은 특성벡터 추출 기법들이 사용되므로 더 많은 계산 시간을 필요로 한다는 단점이 있다. 따라서 계산 시간과 표적 구분 성능 향상은 서로 트레이드 오프(Trade-off) 관계에 있으므로 실제 시스템 적용을 위해서는 계산 시간을 단축시키는 연구가 필요할 것으로 생각된다.
Acknowledgments
본 연구는 2018학년도 한남대학교 학술연구조성비 지원에 의하여 연구되었습니다.
References
-
Q. Li, P. Ilavarasan, J. E. Ross, E. J. Rothwell, K. M. Chen, and D. P. Nyquist, "Radar target identification using a combined early-time/late-time E-pulse technique", IEEE Transactions on Antennas and Propagation, Vol. 46(No. 9), p1272-1278, Aug.), (2002.
[https://doi.org/10.1109/8.719969]

-
H. Kuschel, J. Heckenbach, St. Muller, R. Appel, "Countering stealth with passive, multi-static, low frequency radars", IEEE Aerospace and Electronics Systems Magazine, Vol. 25(No. 9), p11-17, Sep.), (2010.
[https://doi.org/10.1109/MAES.2010.5592986]

-
M. A. Selver, M. M. Taysur, M. Secmen, and E. Y. Zoral, "Hierarchical reconstruction and structural waveform analysis for target classification", IEEE Transactions on Antennas and Propagation, Vol. 64(No. 7), p3120-3129, Jul.), (2016.
[https://doi.org/10.1109/TAP.2016.2567438]

-
I. H. Kim, and I. S. Choi, "Resonance frequency extraction of full-scale radar targets using time-frequency analysis", Journal of KIIT, Vol. 15(No. 6), p87-94, Jun.), (2017.
[https://doi.org/10.14801/jkiit.2017.15.6.87]

-
I. S. Choi, J. H. Lee, and H. T. Kim, "Natural frequency extraction using late-time evolutionary programming-based CLEAN", IEEE Transactions on Antennas and Propagation, Vol. 51(No. 12), p3285-3292, Dec.), (2003.
[https://doi.org/10.1109/TAP.2003.820955]

-
J. H. Lee, S. W. Cho, S. H. Park, and H. T. Kim, "Performance analysis of radar target recognition using natural frequency: Frequency domain approach", Progress In Electromagnetics Research, Vol. 132, p315-345, Jan.), (2012.
[https://doi.org/10.2528/PIER12071107]

-
J. H. Lee, I. S. Choi, and H. T. Kim, "Natural frequency-based neural network approach to radar target recognition", IEEE Transactions on Signal Processing, Vol. 51(No. 12), p3191-3197, Dec.), (2003.
[https://doi.org/10.1109/TSP.2003.818908]

- J. H. Lee, "A study on target recognition using natural frequency", Ph.D. dissertation, POSTECH, Feb.), (1999.
-
J. H. Lee, J. Shim, and H. T. Kim, "Natural frequency extraction from multiple frequency response sample sets using the fitting error", Journal of Electromagnetic Waves and Applications, Vol. 15(No. 5), p583-598, Jan.), (2001.
[https://doi.org/10.1163/156939301X00265]

-
S. J. Lee, I. S. Choi, and D. Y. Chae, "A novel feature extraction method for radar target classification using fusion of early-time and late-time regions", Journal of Electromagnetic Waves and Applications, Vol. 31(No. 10), p1020-1033, May), (2017.
[https://doi.org/10.1080/09205071.2017.1324324]

-
C. H. Park, S. H. Seol, and I. S. Choi, "Performance comparison of correlative target recognition using various radar structure in high frequency band", Journal of KIIT, Vol. 15(No. 5), p97-103, May), (2017.
[https://doi.org/10.14801/jkiit.2017.15.5.97]

- S. J. Lee, "Radar target classification using feature vector fusion based on resonance frequency and waveform structure", Ph.D. dissertation, Hannam University, Feb.), (2017.

2011년 2월 : 한남대학교 전자공학과(공학사)
2013년 2월 : 한남대학교 전자공학과(공학석사)
2017년 2월 : 한남대학교 전자정보통신공학과(공학박사)
2016년 12월 ~ 현재 : (주)MTG 선임연구원
관심분야 : 레이더 신호처리, 레이더 시스템 설계

1998년 2월 : 경북대학교 전자공학과(공학사)
2000년 2월 : 포항공과대학교 전자전기공학과(공학석사)
2003년 2월 : 포항공과대학교 전자전기공학과(공학박사)
2003년 ~ 2004년 : LG전자기술원 선임연구원
2004년 ~ 2007년 : 국방과학연구소 선임연구원
2007년 ~ 현재 : 한남대학교 전자공학과 교수
관심분야 : 레이더 신호처리, 레이더 시스템 설계