위성 SAR 스퀸트 기하에서 NESZ 및 관측폭의 실험적 분석

Ⅰ. 서론

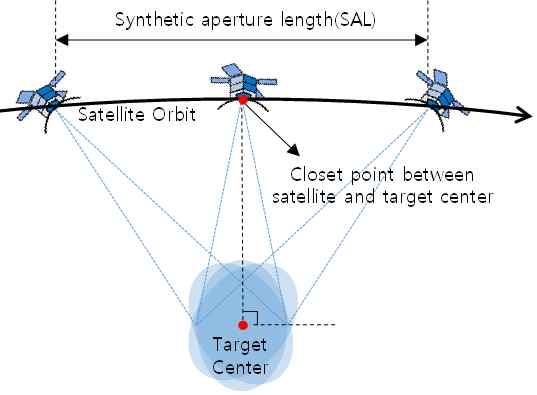
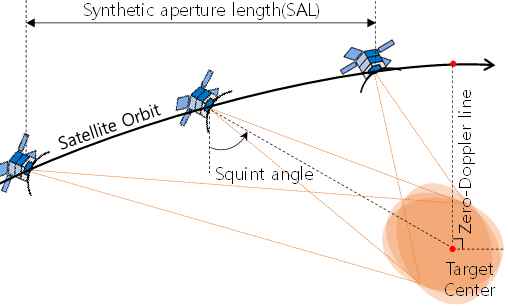
스퀸트를 통한 스포트라이트(Spotlight) 모드는 넓은 관심지역에서 다수의 SAR 영상을 확보 할 수 있는 방식이다. 이 방식은 일반적인 스포트라이트 모드(브로드사이드, Broadside)에 비해 방위방향의 전자적 빔 조향 또는 플랫폼 기동을 크게 하는 방식으로써, 스퀸트 각(Squint Angle)을 통해 안테나의 지향방향을 표적과의 수직 지향방향으로부터 앞 또는 뒤 방향으로 지향하도록 하는 방식이다[1](그림 1,2 참조). 따라서 이 방식은 위성이 표적 중심사이와의 거리가 가장 가까운 지점을 지나지 않고 SAR (Synthetic Aperture Radar) 운용 입사각(Incidence Angle)을 만족하는 지점부터 SAR 영상 데이터를 획득 할 수 있다. 따라서 데이터를 획득 할 수 있는 시간을 보다 확보할 수 있으므로, 영상 획득 수량을 증가시키며 고 해상도의 SAR 영상을 획득 할 수 있다.

Fig. 1.

An example of the SAR data acquisition process in the conventional spotlight mode(broadside)

Fig. 2.

An example of SAR data acquisition process in the spotlight mode with the squint operation

하지만, 스퀸트 운용은 영상품질 변화를 유발한다[2][3]. 과거 참고문헌 [4]-[6]에서는 스퀸트에서의 영상품질 분석으로 해상도, PSLR(Peak to Side-Lobe Ratio), ISLR(Integrated Side-Lobe Ratio)에 대한 분석 및 연구가 수행되었다. 하지만 현재까지 스퀸트에서의 NESZ(Noise Equivalent Sigma Zero) 및 관측폭(Swath Width)에 관한 분석은 미비하다. NESZ 및 관측폭은 SAR 영상품질 중 중요한 요소이기 때문에 SAR 센서의 최적설계를 위해서는 스퀸트 기하에서의 NESZ 및 관측폭 분석이 필수적으로 선 수행되어야 한다.

본 논문에서는 위성 SAR 스퀸트 기하에서 NESZ 및 관측폭 분석을 수행하였다. 특히, 브로드사이드 대비 스퀸트에서의 NESZ 및 관측폭을 분석하였다. 또한 빔폭(Beamwidth) 조정을 이용한 NESZ 및 관측폭 분석 결과 제시를 통해 스퀸트에서 NESZ 및 관측폭에 관한 SAR 센서 설계 방향성을 제시하였다. 이를 위해 SAR 위성 기하에서 스퀸트 각이 주어졌을 때 기하 변화를 [3]의 스퀸트 각과 지상 스퀸트 각(Ground Squint Angle) 관계와 직각구면 삼각형(Right Spherical Triangle) 공식[7]을 이용하여 유도하였다. 본 논문은 [8]을 기반으로 관측폭 분석과 빔폭 조정을 통한 NESZ 및 관측폭 분석을 추가하여 폭 넓은 실험을 수행하였다.

본 논문은 다음과 같이 구성되어있다. 2장에서는 본 논문에서 분석되는 NESZ와 관측폭에 대한 이론을 상세히 기술하였고, 3장에서는 NESZ 및 관측폭 분석을 위한 위성 SAR에서 스퀸트 기하 변화에 대해 기술하였다. 4장에서는 스퀸트에서의 기하 변화를 바탕으로 실험 및 분석을 수행하여 결과를 제시하였다. 끝으로, 5장에서 결론 및 향후 과제에 대해 기술하였다.

Ⅱ. NESZ 및 관측폭 이해

분석에 앞서 본 장에서는 NESZ 및 관측폭에 대한 이해를 돕기 위해 NESZ 및 관측폭에 대한 이론을 상세히 기술하였다.

2.2 관측폭

관측폭은 SAR 센서의 안테나 빔에 의해서 SAR 위성이 지상을 관측할 수 있는 영역의 길이를 의미한다[12].

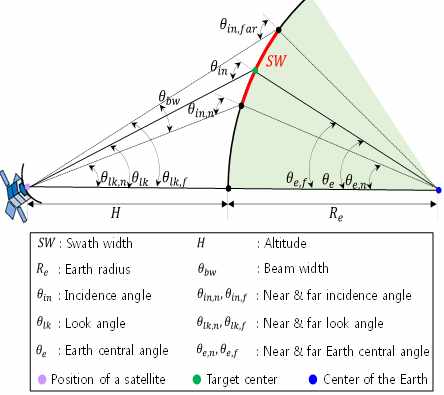
관측폭 SW는 입사각 θ_in, 고도 H, 안테나 빔폭 θ_bw이 주어졌을 때, 다음과 같이 유도될 수 있다 (그림 3 참조).

$\[ SW=R_e({\theta }_{e,f}-{\theta }_{e,n}) \]$

(11)

Fig. 3.

An example of geometry for swath width

R_e는 지구 반지름이며, θ_e,n, θ_e,f는 각각 근 및 먼 지구 중심각으로써 다음과 같이 표현된다.

$\[ {\theta }_{e,n}= {\theta }_{i n,n}-{\theta }_{lk,n} \]$

(12)

$\[ {\theta }_{e,f}= {\theta }_{i n, f}-{\theta }_{lk,f} \]$

(13)

θ_in,n, θ_in,f는 각각 근 및 먼 입사각, θ_lk,n, θ_lk,f는 각각 근 및 먼 관측각으로써 다음과 같이 표현된다.

$\[ {\theta }_{i n,n}= {sin}^{-1}\left[sin\left({\theta }_{lk,n}\right)\frac{R_e+H}{R_e}\right] \]$

(14)

$\[ {\theta }_{i n,f}= {sin}^{-1}\left[sin\left({\theta }_{lk,f}\right)\frac{R_e+H}{R_e}\right] \]$

(15)

$\[ {\theta }_{\mathit{\text{lk}},n}= {\theta }_{\mathit{\text{lk}}}-\frac{{\theta }_{\mathit{\text{bw}}}}{2} \]$

(16)

$\[ {\theta }_{\mathit{\text{lk}},f}= {\theta }_{\mathit{\text{lk}}}+\frac{{\theta }_{\mathit{\text{bw}}}}{2} \]$

(17)

관측각 θ_lk는 다음과 같이 표현된다.

$\[ {\theta }_{lk}= {sin}^{-1}\left[\text{sin}\left({\theta }_{i n}\right)\frac{R_e}{R_e+H}\right]. \]$

(18)

따라서 θ_e,n, θ_e,f를 주어진 입사각, 빔폭, 고도로 표현 가능하기 때문에 식 (11)을 통해 관측폭을 구할 수 있다.

Ⅲ. 스퀸트 및 NESZ 분석을 위한 스퀸트에서의 기하 변화

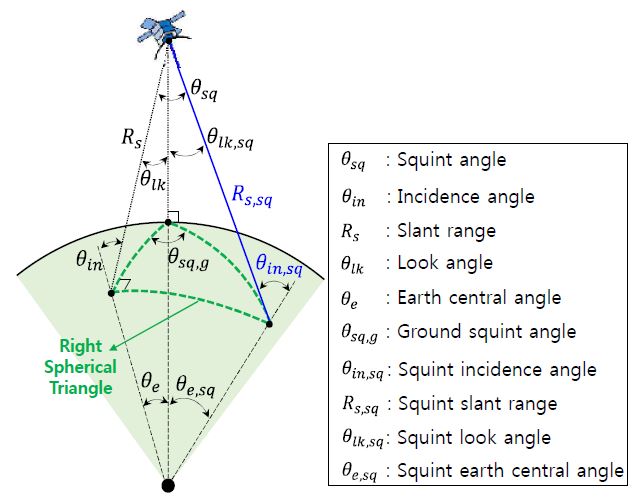
그림 4는 스퀸트에서의 기하 예시이다. 그림에서 θ_sq, θ_sq,g는 각각 스퀸트 각과 지상 스퀸트 각, 즉, 스퀸트 각의 지상으로의 정사영을 의미한다.

그림을 살펴보면 알 수 있듯이, 스퀸트 기하에서는 브로드사이드에서의 입사각과 경사거리 대비하여 스퀸트 입사각 θ_in,sq과 스퀀트 경사거리 R_s,sq로 변화하게 되고, 그 값이 커지는 것을 직관적으로 알 수 있다.

Fig. 4.

An example of squint geometry for deriving the geometry change

이와 연관하여, 식 (10)과 (11)~(18)에서 알 수 있듯이, 모든 조건이 동일하다고 가정할 때 입사각과 경사거리가 NESZ와 관측폭에 주요하게 영향을 주는 요소라는 것을 확인 할 수 있다. 따라서 스퀸트 입사각과 브로드사이드 입사각과의 관계를 알 수 있다면 주어진 변수를 통해 브로드사이드 대비하여 스퀸트에서의 NESZ와 관측폭을 분석할 수 있게 된다.

이를 위해 본 논문에서는 [3]의 수식을 이용하여 주어진 입사각과 고도를 통해 스퀸트 각으로부터 지상 스퀸트 각을 구하고, 유도한 지상 스퀸트 각으로부터 직각 구면 삼각형 공식을 통해 스퀸트 입사각을 구하였다.

첫째, 지상 스퀸트 각을 다음 식으로부터 구하였다[3].

관측각 θ_lk와 지구 중심각 θ_e는 식 (12)와 (18)을 통해 주어진 입사각 θ_in을 통해 구할 수 있기 때문에 주어진 입사각과 스퀸트 각을 통해 지상 스퀸트 각을 구할 수 있다.

둘째, 지상 스퀸트 각과 주어진 입사각을 통해 다음의 수식으로 스퀸트 입사각을 구하였다.

θ_lk,sq 및 θ_e,sq는 각각 스퀸트 관측각, 스퀸트 지구 중심각을 나타내며, θ_lk,sq는 θ_e,sq로 다음 식을 이용하여 구할 수 있다[7].

이때, θ_e,sq는 지각 구면 삼각형 공식을 이용하여 지상 스퀸트 각과 브로드사이드에서의 지구 중심각 θ_e을 통해 다음과 같이 구할 수 있다(직각 구면 삼각형은 그림 4의 녹색 점선 참조).

θ_e는 주어진 입사각과 고도를 통해 계산이 가능하므로, 위 수식들을 이용하여 입사각과 스퀸트 각을 통해 스퀸트 입사각을 구할 수 있게 된다.

Ⅳ. 실험결과 및 분석

본 절에서는 스퀸트 기하에서 NESZ 및 관측폭에 대한 각각의 분석결과 제시하였다. 또한 빔폭 조절을 이용하여 NESZ 및 관측폭 분석 결과 제시를 통해 스퀸트에서 NESZ 및 관측폭에 대한 SAR 센서 설계 방향성을 제시하였다. 브로드사이드 대비 상대적인 분석을 위해서 본 절에 제시한 결과 값은 절대 값이 아닌 브로드사이드 대비한 스퀸트 기하에서의 NESZ 및 관측폭 차이를 제시하였다.

4.1 실험환경

실험 변수를 표 1과 같이 설정하였다. NESZ와 관측폭은 위성이 합성 개구면 길이를 이동하는 동안의 누적 평균값을 사용하였다. 안테나는 파라볼릭 (Parabolic)안테나 식을 적용하였다[13].

Table 1.

Experimental data

4.2 실험결과 및 분석

4.2.1 스퀸트 기하에서의 입사각 변화 분석

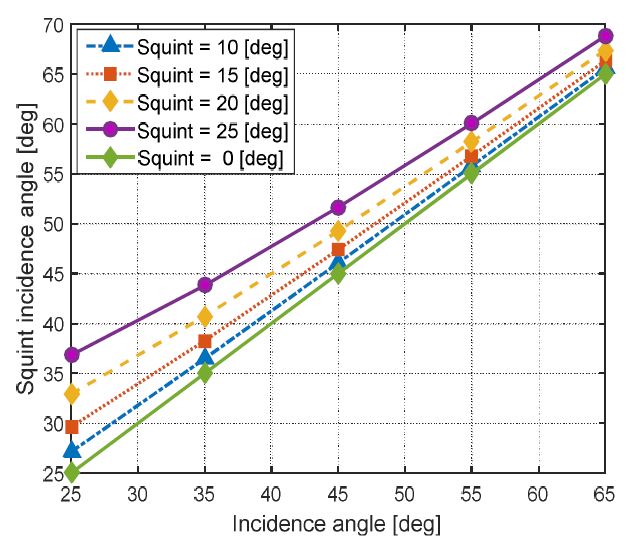
3장에서 언급하였듯이 스퀸트 기하에서 NESZ 및 관측폭에 주요하게 영향을 미치는 요소는 스퀸트 입사각이라는 것을 알 수 있다. 따라서 본 절에서는 본 논문의 분석이 유효함을 보이고자 스퀸트 기하에서의 입사각 변화를 우선적으로 분석하였다.

그림 5와 표 2의 결과를 살펴보면, 특정 입사각에서 스퀸트 각이 증가 할수록 입사각의 변화량이 커진다. 그 이유는 특정 고도에서 스퀸트 각이 클수록 경사거리가 길어지기 때문이다. 또한, 입사각이 작을수록 스퀸트에 의한 입사각 변화량이 작아진다. 그 이유는 입사각이 작을수록 경사거리가 짧기 때문에 스퀸트에 의한 영향에 더 민감하기 때문이다.

Fig. 5.

The results of the squint incidence angle with respect to the incidence angle

Table 2.

The results of squint incidence angle with respect to the incidence angle (unit: [deg])The results of squint incidence angle with respect to the incidence angle(unit: [deg])

또한, 본 절에서는 스퀸트가 0° 일 때, 즉, 브로드사이드 일 때의 결과를 추가 제시하였다. 결과를 보면 알 수 있듯이 시뮬레이션 결과가 입사각 입력 값과 동일하다는 것을 확인 할 수 있다.

상기 경향성 및 결과를 통해 본 논문에서 유도한 기하 변화가 유효하다는 것을 판단 할 수 있었다.

4.2.2 스퀸트 기하에서의 NESZ 변화 분석

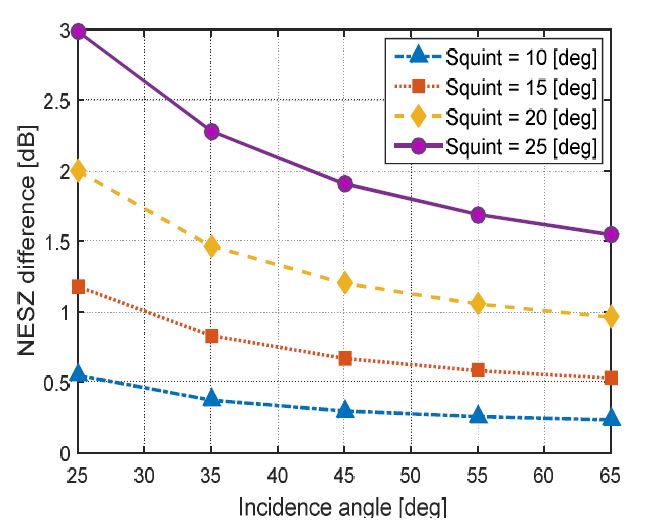
그림 6과 표 3의 결과를 보면, NESZ 변화는 입사각 변화와 같은 추세로 변화하는 것을 관찰 할 수 있다. 추가적으로 스퀸트 기하에서는 브로드사이드 대비 NESZ가 저하되는 것을 관찰 할 수 있다. 즉, NESZ가 증가하는 것을 관찰 할 수 있다. 그 이유는 설계 조건이 동일 할 때, 식 (10)의 분모 항에 있는 입사각과 경사거리가 증가하기 때문이다.

Fig. 6.

The results of the NESZ change amount with respect to the incidence angle given squint angle

Table 3.

The results of NESZ change amount with respect to the incidence angle given squint angle(unit: [dB])

4.2.3 스퀸트 기하에서의 관측폭 변화 분석

그림 7과 표 4의 결과를 보면, 스퀸트 기하에서는 브로드사이드 대비하여 관측폭이 커진다. 즉, 관측할 수 있는 지상범위가 커지는 장점이 있다. 그 이유는 스퀸트 운용 시 경사거리가 커지게 되어 동일 빔폭을 갖는 안테나가 지표면을 관측 할 수 있는 영역이 넓어지기 때문이다. NESZ와는 다르게 큰 입사각에서 스퀸트에 의한 변화량이 더 커지는 것을 확인 할 수 있다. 그 이유는 큰 입사각에서는 작은 입사각 변화가 있더라도, 빔폭에 의해 관측할 수 있는 지상 범위가 큰 입사각에서 보다 크게 변화되기 때문이다.

Fig. 7.

The results of the swath width change amount with respect to the incidence angle given squint angle

Table 4.

The results of swath width change amount with respect to incidence angle given squint angle(unit: [km])

4.2.4 빔폭 조정을 통한 NESZ 및 관측폭 분석 및 설계 방향성 제시

앞 절의 결과에서 알 수 있듯이, 스퀸트 운용에서는 NESZ는 저하되고 관측폭은 커지는 것을 확인 할 수 있다. 따라서 임무에서 요구되는 관측폭을 만족시키면서 여분의 관측폭을 감소시키면 NESZ의 저하를 완화시킬 수 있다. 이를 달성하기 위한 방법으로는 빔폭을 좁게 설계하면서 안테나 이득을 증가시키는 방법이 있다. 따라서 본 실험에서는 모든 설계 조건이 동일하다고 가정하고, 빔폭을 좁게 선정하여 관측폭의 크기를 줄이며, NESZ의 저하를 감소시키는 설계 결과를 제시하였다.

NESZ는 입사각이 작을수록, 관측폭은 입사각이 클수록 값의 변화가 크므로 중간 지점에 해당하는 입사각 45°에서 본 분석을 수행하였다. 또한, 해당 분석결과를 효과적으로 관찰하기 위해서, 즉, 관측폭 여유가 비교적 큰 스퀸트 각 20° 및 25°에서 실험을 수행하였다. 이 조건을 기준으로 본 실험에 적용된 빔폭과 안테나 이득은 표 5와 같다. 여기서 빔폭과 안테나 이득은 [13]을 참조하여 설정하였다. 스퀸트 25°에서는 기존 빔폭 값 대비하여 [13]에서 나열된 바와 같이 최대로 줄일 수 있는 빔폭을 적용하였으며, 스퀸트 20°에서는 위성이 합성 개구면 길이 중심에 있을 때, 브로드사이드 대비 최대로 줄일 수 있는 관측폭 크기 범위로부터 빔폭을 도출 하였다.

Table 5.

The experimental variable for the comparative analysis of NESZ and swath width

표 6은 본 실험의 결과이다. 결과에서 확인 할 수 있듯이, 본 논문에서는 스퀸트 운용으로 확보되는 관측폭 크기를 감소시키고, 즉, 안테나 빔폭을 좁게 하고 안테나 이득을 증가시킴으로써 NESZ 저하량을 감소시킬 수 있다는 결론을 얻을 수 있었다. 따라서 스퀸트에서는 브로드사이드보다 넓은 관측폭을 확보 할 수 있으므로, 스퀸트에서 NESZ 및 관측폭 관련한 SAR 센서 설계 시에는 빔폭을 좁게 설계하는 방향으로 설계가 필요할 것으로 판단된다.

Table 6.

The results of difference change amount for NESZ and swath before/after applying design change of beamwidth

다만, 본 논문의 분석결과는 안테나 이득, 빔폭, 그리고 기하에 의한 영향성만을 고려하였다. 즉, PRF, 대역폭 등을 동일하게 설정하였으므로, 향 후 모든 변수들을 설계에 반영함으로써 보다 사실적인 분석이 수행되어야만 정확한 방향성 제시가 될 수 있을 것이라 판단된다.

Ⅴ. 결론 및 향후 과제

본 논문에서는 위성 SAR의 영상품질 중 중요한 요소인 NESZ와 관측폭에 대하여 이해하고, 스퀸트 기하에서의 기하 변화를 유도하였다. 유도된 기하를 바탕으로 브로드사이드 대비 스퀸트 기하에서의 NESZ 및 관측폭 변화를 분석하였다. 분석결과, 스퀸트 기하에서 NESZ 및 관측폭은 증가하는 것을 관찰 할 수 있었다. 즉, NESZ 성능은 저하되고, 관측폭 성능은 향상되는 것을 알 수 있었다. 또한, NESZ는 입사각이 작을수록 저하량이 커지는 반면에 관측폭은 입사각이 클수록 크기 변화량이 커지는 것을 확인 할 수 있었다. 이러한 관찰을 바탕으로 본 논문에서는 빔폭 조절을 통해 NESZ 저하를 완화시키는 방안을 고려하였으며, 분석 결과를 추가 제시였다. 분석 결과를 통해, 스퀸트에서의 SAR 센서 설계 시에는 요구되는 관측폭을 만족하는 범위에서 빔폭은 좁게, 그리고 안테나 이득은 증가시키도록 설계해야 한다는 것을 알 수 있었다. 즉, 스퀸트에서는 확보되는 관측폭 여분을 감소시키고 NESZ 저하를 줄이는 방향으로 설계를 수행해야 한다는 것을 알 수 있었다. 따라서 본 논문의 분석은 스퀸트 운용 시의 영상품질 분석 및 설계 시에 활용 할 수 있을 것이라고 판단된다.

하지만 본 논문에 사용된 변수는 실제 위성 운용 설계 값이 아니다. 그리고 실제 위성 운용을 위한 SAR 센서 설계에서는 성능이 최적화되도록 입사각 별로 대역폭, PRF 등이 상이하게 설계된다. 또한 실제 환경에서는 입사각에 따라 표적의 유효반사 면적이 상이하다. 하지만 본문에서는 입사각 별로 기하 및 안테나 이득 이외의 변수가 모두 동일하다고 가정하였다. 즉, 기하 및 안테나 빔폭에 따른 영향성을 주요하게 고려하였다. 또한, SAR 센서 성능 관점에서만 고려하였기 때문에 향후 보다 실제적인 변수, 설계 수치, SAR 센서 이외의 구성품 등을 고려하여 보다 실제적인 분석과 방향성 제시가 필요할 것으로 판단된다.

References

• G. W. Davidson, and I. G. Cumming, "Signal Properties of Spaceborne Squint-Mode SAR", IEEE Transactions on Geoscience and Remote Sensing, Vol. 35(No. 3), p611-617, May), (1997. [https://doi.org/10.1109/36.581976]
• G. W. Davidson, I. G. Cumming, and M. R. Ito, "A Chirp Scaling Approach for Processing Squint Mode SAR Data", IEEE Transactions on Aerospace and Electronic Systems, Vol. 32(No. 1), p121-133, Jan.), (1996. [https://doi.org/10.1109/7.481254]
• U. Naftaly, "Squint Angle Limitations for Space-Borne Spot SAR Imaging", 7th European Conference on Synthetic Aperture Radar, Vol. 3, p185-188, Jun.), (2008.
• B. Sun, H. Xu, Y. Wang, and W. Yang, "Orthogonal Resolution Analysis for Squint SAR Image", in Proceedings of 11th European Conference on Synthetic Aperture Radar, p401-404, Jun.), (2016.
• L. Shu, W. Ying, and Z. Yigong, "Exact Analysis of the Azimuth Resolution Characters of Squint SAR", Journal of Systems Engineering and Electronics, Vol. 15(No. 4), p502-506, Dec.), (2004.
• Z. Li, X. Zhao, and Z. Ding, "Analysis of Diving Squint SAR Resolution", in Proceedings of 2011 IEEE CIE International Conference on Radar, p875-878, Oct.), (2011.
• J. R. Wertz, D. F. Everett, and J. J. Puschell, "Space Mission Engineering: The NEW SMAD", Space Technology Library, p173, 976, Jul.), (2011.
• S. S. Yoon, M. J. Bae, and K. D. Cho, "An Analysis of NESZ Degradation given Squint in Space-Borne SAR", in Proceedings of 2017 Korea Institute of Military Science and Technology(Domestic Conference), Jun.), (2017.
• M Younis, S. Huber, A. Patyuchenko, F. Bordoni, and G. Krieger, "Performance Comparison of Reflector- and Planar-Antenna Based Digital Beam-Forming SAR", International Journal of Antennas and Propagation, Vol. 2009, Article ID 614931, p13 pages, May), (2009.
• Y. K. Chan, and V. C. Koo, "An introduction to synthetic aperture radar (SAR)", Progress In Electromagnetics Research B, Vol. 2, p27-60, (2008). [https://doi.org/10.2528/PIERB07110101]
• J. C. Curlander, and R. N. McDonough, "Synthetic Aperture Radar Systems and Signal Processing", John Wiley & Sons Inc., p15, (1991).
• A. Moreira, P. Prats-Iraola, M. Younis, G. Krieger, I. Hajnsek, and K. P. Papathanassiou, "A Tutorial on Synthetic Aperture Radar", IEEE Geoscience and Remote Sensing Magazine, Vol. 1(No. 1), p6-43, Mar.), (2013. [https://doi.org/10.1109/MGRS.2013.2248301]
• W. L. Stutzman, and G. A. Thiele, "Antenna Theory and Design", John Wiley & Sons Inc., p320-321, (1988).