시가지 I_o분포 전파환경에서 전송가능 대역폭 평가척도와 새로운 누적확률지 평가차트

Ⅰ. 서론

최근의 이동무선 전파환경은 정상파(직접파 또는 직접회절파)성분의 비율이 커지는 경우가 많고, 일반적인 레일리(Rayleigh) 분포의 전파환경이라기 보다는 Nakagami-Rice 분포(I_o분포)환경으로 보는 것이 타당하다[1]-[4]. 또한 I_o분포환경에서는 전송가능 대역폭 평가파라미터로, 주파수가 서로 다른 2개 전파의 전계강도에 대한 상관계수보다는 dB값의 차의 표준편차 또는 dB값의 차의 절대치 값의 평균을 그 평가척도로 이용하는 것이 타당하다[5]. 따라서 I_o분포환경에서는 올바른 전송가능 대역폭의 평가척도를 결정하기 위해서는 기존의 레일리 누적확률지를 대신할 수 있는 새로운 누적확률지 평가차트를 고안할 필요가 있다.

본 논문에서는 전송가능 대역폭의 평가척도를 결정하기 위하여 기존의 레일리 누적확률지를 대신하는 새로운 전계강도 누적확률 평가차트를 고안한다. 우선, 레일리 분포 및 I_o분포를 포함한 시가지 모든 전파전파특성을 표현할 수 있는 범용적인 m-분포 모델을 이용하여 2개의 수신전파의 전계강도로부터 구해지는 dB값의 차이에 해당하는 확률분포 식을 유도한다. 그로부터 dB값의 차의 절대치에 대한 누적확률분포 식을 구하고 새로운 누적확률 평가차트를 구한다.

본 논문의 구성을 다음과 같다. 제 2장에서는 m-분포모델이 시가지에서의 I_o분포모델을 포함한 범용적인 분포모델임을 이론적으로 설명한다. 또한, m-분포 모델의 dB값의 차의 분포 식(확률밀도함수)을 유도하고 컴퓨터 시뮬레이션으로부터 그 타당성을 설명한다. 제 3장에서 레일리 분포를 포함하는I_o분포의 dB값의 차의 절대치의 누적분포를 유도하고 전송가능 대역폭의 평가척도와 새로운 누적확률평가 차트를 구한다. 또한 이론해석과 컴퓨터 시뮬레이션에 의해 그 타당성을 검토하고 전송가능 대역폭을 가늠하는 정량적 평가척도를 기술한다. 마지막으로 제 4장에서는 결론을 기술한다.

Ⅱ. 시가지 수신전계 분포특성해석

2.1 m-분포 모델

시가지 이동무선 수신신호의 전계강도변동(포락선 R)을 표현하는 분포에는, I_o분포를 포함할 수 있는 분포 식으로 일반적인 m-분포가 있으며, 그 확률밀도함수는 식 (1)로 주워진다[6].

$\[ p\left(R\right)=\frac{2m^m}{\Gamma \left(m\right){\Omega }^m}{R}^{2m-1}\text{exp}\left(-m\frac{R^2}{\Omega }\right) \]$

(1)

여기서，

<R²>=Ω, $$ m=\frac{{\Omega }^2}{〈{\left(R^2-\Omega \right)}^2〉}\ge \frac{1}{2}$$

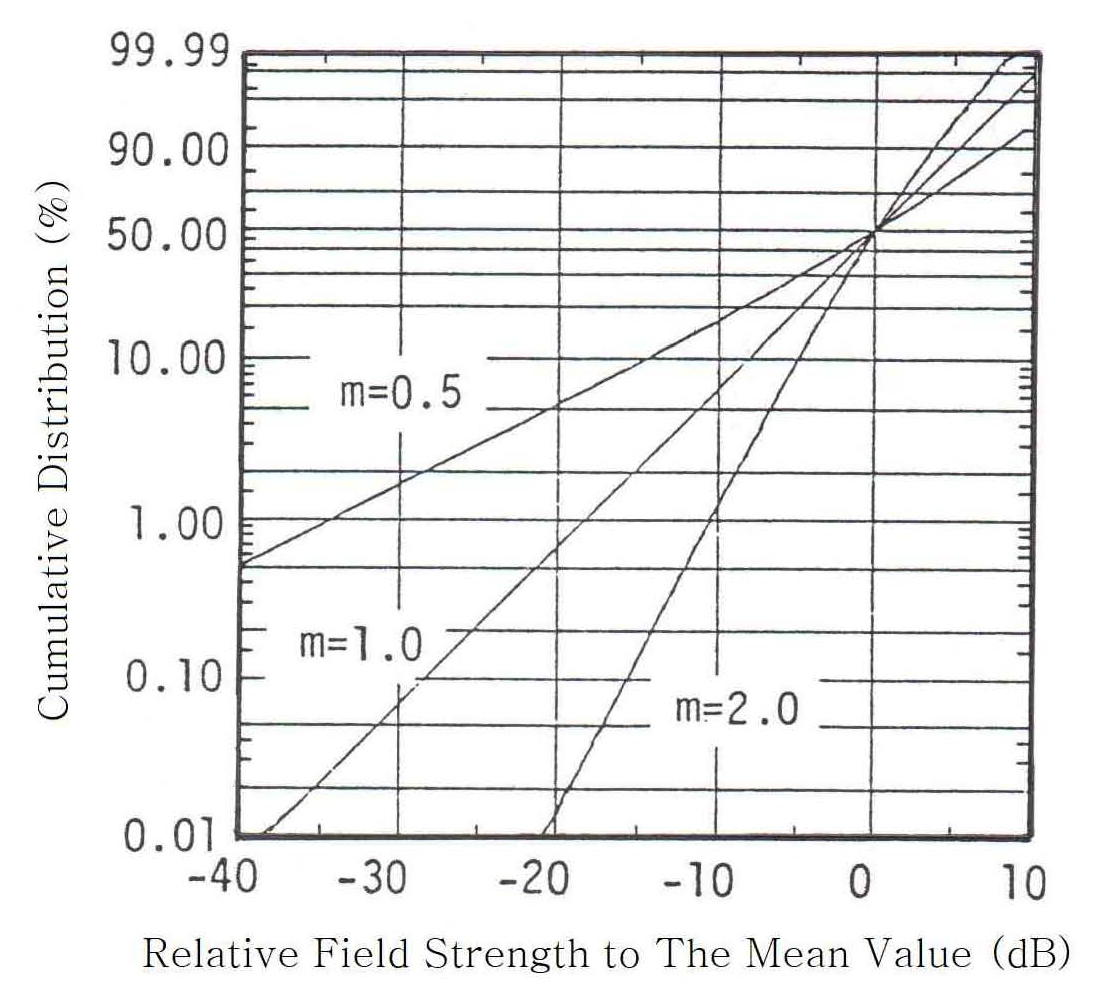
Γ(•)는 감마(Gamma) 함수이며, <•>는 앙상블(Ensemble) 평균을 나타낸다. m-분포의 전계강도 누적분포 계산 예를 그림 1에 나타낸다.

Fig. 1.

Calculation example of field strength cumulative distribution for the m-distribution

일반적으로 파라미터 m은 페이딩의 깊이를 나타내며 m이 작을수록 페이딩이 심하다는 것을 나타낸다. m=1인 경우가 다음의 식 (2)와 같이 레일리 분포 식(확률분포))과 일치하며, 1/2≤m〈1인 경우가 레일리 분포보다 페이딩이 심한 경우를 나타낸다. 또한, m≥1의 경우가 I_o분포에 상당하며 근사적으로 I_o분포를 표현한다. 그리고 m이 클수록 페이딩의 깊이가 작게 됨을 나타낸다[6].

$\[ \begin{array}{c}p\left(R\right)=\frac{R}{{\sigma }^2}\text{exp}\left(-\frac{R^2}{2{\sigma }^2}\right),\\ F\left(R\right)=1-\text{exp}\left(-\frac{R^2}{2{\sigma }^2}\right)\end{array} \]$

(2)

2.2 m-분포 모델의 dB값의 차의 분포

본 절은 m-분포의 2개의 수신전파 포락선의 dB값의 차에 대한 분포를 고려한다. 복소상관계수 ρ를 갖는 2개의 포락선 R₁, R₂의 비 V=R₁/R₂의 확률밀도 p(V)는 식 (3)과 같이 주워진다[6].

$\[ \begin{array}{c}p\left(V\right)=\frac{2{\left(1-{\left|\rho \right|}^2\right)}^m{\left(\frac{{\Omega }_1}{{\Omega }_2}\right)}^m{V}^{2m-1}}{B\left(m,m\right){\left(V^2+\frac{{\Omega }_1}{{\Omega }_2}\right)}^{2m}}•\\ {\left\{1-\frac{4{\left|\rho \right|}^2\frac{{\Omega }_1}{{\Omega }_2}{V}^2}{{\left(V^2+\frac{{\Omega }_1}{{\Omega }_2}\right)}^2}\right\}}^{-(m+\frac{1}{2})}\end{array} \]$

(3)

여기서, $$ {\Omega }_1=〈{R_1}^2〉,{\Omega }_2=〈{R_2}^2〉$$

B(• , •): beta 함수, $$ B(m,m)=\frac{\Gamma (m)\Gamma (m)}{\Gamma (2m)}$$

단, 수식 (3)에서 |ρ|²은 전력의 상관계수와 같고, 또한 전계강도의 상관계수와 거의 일치한다[7][8].

2개의 전계강도 R₁, R₂의 dB값의 차 x=20logV의 확률밀도 p(x)는 2파의 평균전력 Ω₁, Ω₂가 같은 경우에는 상기의 식 (3)으로부터 다음 식 (4)로 나타낼 수 있다.

$\[ \begin{array}{c}p\left(x\right)=\frac{ln10}{10}•\frac{{\left(1-{\left|\rho \right|}^2\right)}^m{10}^{\frac{mx}{10}}}{B\left(m,m\right){\left({10}^{\frac{x}{10}}+1\right)}^{2m}}•\\ {\left\{1-\frac{4{\left|\rho \right|}^2{10}^{\frac{x}{10}}}{{\left({10}^{\frac{x}{10}}+1\right)}^2}\right\}}^{-(m+\frac{1}{2})}\end{array} \]$

(4)

또한, 2파의 평균전력이 같은 경우에는 p(-x)=p(x)이므로 dB값의 차의 절대치 y=|x|의 확률밀도 p(y)는 식 (5)와 같다.

$\[ \begin{array}{c}\left(y\right)=\frac{ln10}{5}•\frac{{\left(1-{\left|\rho \right|}^2\right)}^m{10}^{\frac{my}{10}}}{B\left(m,m\right){\left({10}^{\frac{y}{10}}+1\right)}^{2m}}•\\ {\left\{1-\frac{4{\left|\rho \right|}^2{10}^{\frac{y}{10}}}{{\left({10}^{\frac{y}{10}}+1\right)}^2}\right\}}^{-(m+\frac{1}{2})},\left(y\ge 0\right)\end{array} \]$

(5)

식 (4)를 이용하여 계산한 dB값에 대한 차의 누적분포의 이론값을 그림 2에 나타낸다. 그림 2(a)는 m=1인 경우의 레일리 분포 시의 상관계수를 변화시킨 경우로 상관계수가 커질수록 dB값의 차는 작게 된다. 그림 2(b)는 m을 변화시킨 경우로 상관계수가 같더라도 m이 커지게 되면, 즉 정상파 성분의 비율이 커질수록 페이딩이 약해지기 때문에 dB값의 차가 작아지는 이유를 잘 나타내고 있다.

한편, m=1인 레일리 분포의 경우에서, 두 개의 전파가 독립적인 경우(즉, |p²|=0)에는 누적분포 계산이 가능하다. dB값의 차의 확률밀도와 누적분포 식은 식 (4)로부터 다음의 식 (6)과 같이 유도할수가 있다(부록 1).

$\[ \begin{array}{c}p\left(x\right)=\frac{\text{ln}10}{10}•\frac{{10}^{\frac{x}{10}}}{{\left({10}^{\frac{x}{10}}+1\right)}^2}\\ F\left(x\right)=1-\frac{1}{{10}^{\frac{x}{10}}+1}\end{array} \]$

(6)

Fig. 2.

Calculation example of dB difference value distribution for the m-distribution

그림 3(a)에 식 (6)에 대한 그래프 모두를 나타낸다. 그림 3(b)는 이때의 누적분포를 정규확률지(도수분포곡선을 근거로 하여 그려진 누적백분율곡선)에 그려봤다. 이로부터 m=1인 경우의 레일리 분포 전파화경에서 2개의 전파가 서로 독립적인 경우의 누적분포는 정규분포와 유사함을 나타낸다. 그리고 수치계산으로부터 독립적인 레일리 분포의 dB값의 차의 표준편차는 7.88로 계산된다(부록1).

Fig. 3.

Distribution of dB difference value for independent Rayleigh distribution

또한, 독립한 레일리 분포의 dB값의 차의 절대치의 확률밀도와 누적분포는 식 (5)로부터 다음 식 (7)과 같이 유도 된다(부록2).

$\[ \begin{array}{c}p\left(y\right)=\frac{\text{ln}10}{5}•\frac{{10}^{\frac{y}{10}}}{{\left({10}^{\frac{y}{10}}+1\right)}^2}\left(y\ge 0\right)\\ F\left(y\right)=1-\frac{2}{{10}^{\frac{y}{10}}+1}\left(y\ge 0\right)\end{array} \]$

(7)

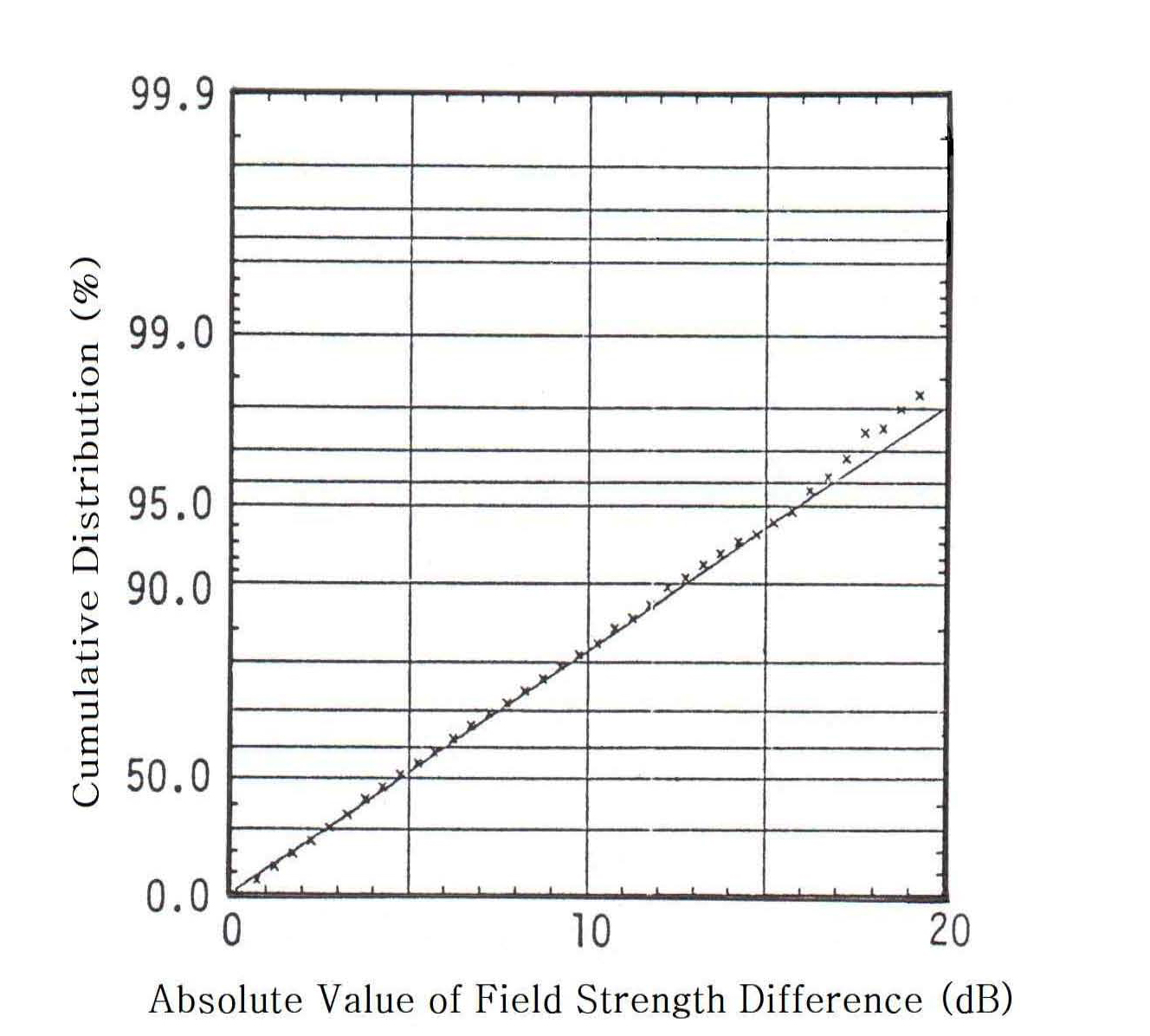
상기 식 (7)의 경우는 평균치가 6.02로 계산된다(부록2). 식 (7)의 누적분포가 직선이 되도록 표현하는 확률지(누적백분율곡선이 직선이 되도록 한 확률지)를 그림 4에 나타낸다. 그림 4에서 직선이 이론 계산치를 나타낸 것이고 x표시가 시뮬레이션 결과 값을 나타낸다. 그림 4에서 이론값과 시뮬레이션 값은 잘 일치하여 시뮬레이션의 타당성을 입증하고 있다. 이와 같이 독립적인 레일리 분포의 dB값의 차의 절대치의 분포(I_o분포) 직선이 되도록 한 그림 4의 새로운 누적확률지를 이용하면 전송가능 대역폭의 평가 및 각종 전파전파특성개선 등을 검토할 수 있다.

Fig. 4.

Absolute value distribution for the dB values of independent Rayleigh distribution

Ⅲ. 전송가능 대역폭 평가척도

3.1 dB값의 차의 절대치 누적분포

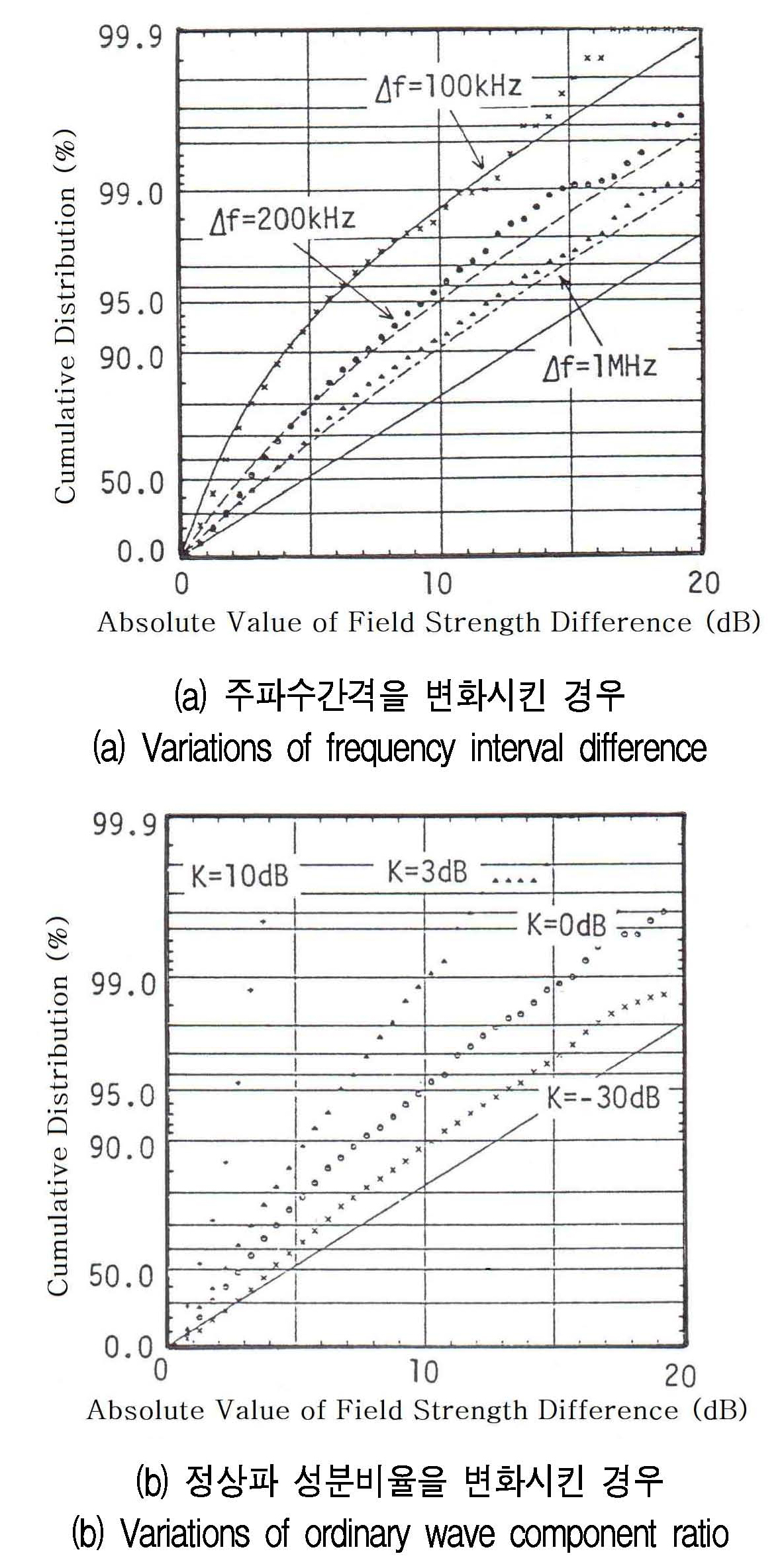
그림 5에 레일리 분포를 포함하는 I_o분포의 dB값의 차의 절대치의 누적분포를 나타낸다. 그림 5(a), (b)는 시뮬레이션결과와 시뮬레이션의 전계강도로부터 계산한 상관계수를 식 (5)에 대입하여 이론 계산치를 나타냈다.

그림 5(a)는 레일리 분포의 경우로 주파수간격이 커질수록 dB값의 차의 절대치가 작게 되는 확률이 감소하여 전송가능 대역폭이 좁게 된다.

Fig. 5.

Absolute value distribution for the dB values of Io distribution

예를 들면, 2파의 dB값의 차가 ±5dB 이내로 될 수 있는 비율은 주파수 간격 Δf가 100kHz(x표시: 시뮬레이션 값, 실선: 이론값）일 때 93%정도인 반면에, Δf가 1MHz(⧍표시: 시뮬레이션 값, 파선:이론값)일 경우에는 67% 정도로 나타난다. 또한, 주파수 간격이 크게 되면 될수록 I_o분포의 경우에 해당하는 직선 값에 가깝게 근접하게 됨을 보이고 있다.

그림 5(b)는 I_o분포의 정상파 성분의 비율 K를 변화시킨 경우이며, 시뮬레이션 결과(표시: ×,○,⧍,+)만을 나타냈다. 그림 5(b)로 부터, 정상파 성분 비율 K(K²=정상파성분/불규칙파성분)가 클수록 dB값의 차의 절대치가 작아지는 확률이 증가하여 전송가능 대역폭이 넓게 됨을 알 수 있다. 이와 같이, I_o분포의 dB값의 차의 절대치의 누적분포로부터 dB값의 차의 절대치의 증감 여부를 인식하여 전송가능 대역폭의 척도로 가늠할 수 있다.

3.2 새로운 누적확률지 평가 및 고찰

그림 6(a)에 레일리 분포인 경우의, dB값의 차의 표준편차와 상관계수의 관계를 나타낸다. 그림 6(b)는 dB값의 차의 절대치 평균과 상관계수의 관계이다. 실선으로 표시한 것이 이론값이고, 점으로 표시한 것이 시뮬레이션 결과이다. 이론값은 식 (4)로부터 계산하였다. 시뮬레이션에서는 통로 차의 평균을 변화시켜서 여러 가지 상관계수를 구하였다. 그림 6(a), (b)의 두 경우 모두 상관계수와 잘 일치하여 시뮬레이션의 타당성을 입증하고 있다. 따라서 dB값의 차의 표준편차와 dB값의 차의 절대치 평균은 전송가능 대역폭의 평가척도로 사용할 수 있음을 알 수 있다.

전송가능 대역폭은 디지털 전송의 오류율이 어떤 기준치에 달하는 대역폭의 값으로 결정하지만, 특정의 전파전파 모델과 오류율과의 관계는 아직까지 소수의 문헌에만 보고되어 있다[9][10]. 일반적으로는 오류율이 아니라 상관계수가 0.9 또는 0.5가 되는 주파수간격을 전송가능 대역폭으로 보고 있다[11]. 그림 6(a), (b)에 표시한 바와 같이 상관계수 0.9는 dB값의 차의 표준편차가 3.61, dB값의 차의 절대치의 평균이 2.39이다.

Fig. 6.

Relations between corelation coefficient and dB value difference in Rayleigh distribution

또한 상관계수 0.5는 표준편차가 6.33, 절대치 평균이 4.65에 대응한다. 따라서 dB값의 차의 표준편차가 3~7dB, 그리고 dB값의 차의 절대치 평균이 2~5dB가 되는 주파수간격이 전송가능 대역폭으로 가늠할 수 있다고 생각된다. 결과적으로, 상관계수는 레일리 분포의 경우에만 전송가능 대역폭의 평가 방법이 될 수 있지만, dB값의 차는 I_o분포도 포함하며 오류율에도 대응하는 것으로 예상되어 통상적인 전송가능 대역폭의 평가 방법이 될 수 있다. 그 평가 척도로서 I_o분포의 dB값의 차의 절대치의 누적분포를 나타내는 확률지 차트를 사용함이 올바른 방법이라 생각한다.

Ⅳ. 결 론

본 논문에서는 시가지 전파전파모델을I_o분포모델로 가정하고 전송가능 대역폭의 평가척도와 새로운 누적확률평가 차트를 구하였다. 이론해석과컴퓨터 시뮬레이션에 의한 dB값의 차의 표준편차와 상관계수와의 관계, 그리고 dB값의 차의 절대치 평균과 상관계수와의 관계부터 새로이 고안한 누적확률지 평가차트가 전송가능 대역폭의 평가척도로 사용할 수가 있음을 확인하였다. 결론적으로 시가지I_o분포 전파환경에서는 dB값의 차의 표준편차가 3~ 7dB, 그리고 dB값의 차의 절대치 평균이 2~5dB가 되는 주파수간격이 전송가능 대역폭으로 평가되었다. 그 평가척도로 I_o분포의 dB값의 차의 절대치의 누적분포를 나타내는 누적확률지 평가차트를 사용함이 타당한 방법이라 생각된다．

Acknowledgments

이 논문은 부경대학교 자율창의학술연구비(2017년)에 의하여 연구되었음.

References

• S. Geng, J. Kivinen, X. Zhao, and P. Vainikainen, "Millimeter-Wave Propagation Channel Characterization for Short-Range Wireless Communications", IEEE, Trans. on Vehicular Technology, Vol. 58(No. 1), p3-13, Jan.), (2009. [https://doi.org/10.1109/TVT.2008.924990]
• D. M. Rose, T. Jansen, and T. Kürner, "Indoor to Outdoor Propagation-Measuring and Modelling of Femto Cells in LTE Networks at 800 and 2600 MHz", in Proc. IEEE GLOBECOM Workshop (GC Workshops 2011), Houston, Texas, p203-207, Dec.), (2011.
• L. Cheng, B. E. Henty, D. D. Stancil, F. Bai, and P. Mudalige, "Mobile Vehicle-to-Vehicle Narrow- Band Channel Measurement and Characterization of the 5.9 GHz Dedicated Short Range Communication (DSRC) Frequency Band", IEEE, Journal on Selected Areas in Communications, Vol. 25(No. 8), p1501-1516, Oct.), (2007. [https://doi.org/10.1109/JSAC.2007.071002]
• Deock-Ho Ha, "Radio Channel Model Suitable for The Next Generation Wireless Access Vehicular Environment Technology", The Journal of KIIT, Vol. 12(No. 4), p43-50, Apr.), (2014. [https://doi.org/10.14801/kiitr.2014.12.4.43]
• Deock-Ho Ha, "A Study on Estimation Method of Practicable Transmission Bandwidth in Femto Cell Propagation Environments", The Journal of KIIT, Vol. 15(No. 4), p55-62, Apr.), (2017. [https://doi.org/10.14801/jkiit.2017.15.4.55]
• M. Nakagami, "The m-Distribution - A General Formula of Intensity Distribution of Rapid Fading", in Statistical Methods of Radio Wave Propagation, W. C. Hoffman ) (ed., Pergamon Press, (1960). [https://doi.org/10.1016/B978-0-08-009306-2.50005-4]
• R. H. Clarke, "A Statistical Theory of Mobile-Radio Reception", The Bell System Technical Journal, Vol. 47(No. 6), p957-1000, Aug.), (1968. [https://doi.org/10.1002/j.1538-7305.1968.tb00069.x]
• J. N. Pierce, and S. Stein, "Multiple Diversity with Nonindependent Fading", Proc. IRE, p89-104, Jan.), (1960. [https://doi.org/10.1109/JRPROC.1960.287384]
• W. C. Jakes Jr. (editor), "Microwave Mobile Communications", John Wiley & Sons, (1974).
• D. R. Hummels, and F. W. Ratcliffe, "Calculation of Error Probability for MSK and OQPSK Systems Operating in a Fading Multipath Environment", IEEE Trans. on Vehicular Technology, Vol. 30(No. 3), p112-120, Sep.), (1981. [https://doi.org/10.1109/T-VT.1981.23891]
• D. C. Cox, and R. P. Leck, "Correlation Bandwidth and Delay Spread Multipath Propagation Statistics for 910 MHz Urban Mobile Radio Channels", IEEE Trans, Vol. Com-23(No. 11), p1271-1280, Nov.), (1975.