백색잡음 테스트를 통한 가우시안 잡음 예측

Ⅰ. 서 론

ISP(Image Signal Processor)는 이미지 센서로부터 출력되는 CFA(Color Filter Array) 패턴[1]의 영상 데이터로부터 최적화된 YCbCr 색공간 데이터를 출력하기 위해서 일련의 알고리즘들을 수행하는 주체를 지칭한다. ISP[2]에서 수행되는 알고리즘들은 표본화된 RGB 공간 혹은 CFA 공간, RGB 공간, YCbCr 공간과 같이 3개의 색 공간에서 구분되어 수행된다. 기본적으로 탑재되는 알고리즘에는 렌즈 음영 보정(Lens Shading Correction), 색보간(Color Interpolation), 잡음 제거(Noise Reduction), 감마 보정(Gamma Correction), 색보정(Color Correction), 색공간 변환(Color Space Conversion), 자동 색온도보정(AWB, Auto White Balancing), 자동노출보정(AEC, Auto Exposure Control)등이 포함되어 있으며, 최적의 색재현과 선예도(Sharpness) 향상을 위해서 다양한 알고리즘이 지속적으로 개발되고 적용되고 있다. 나열된 알고리즘 중에서는 최종 영상의 선예도에 직접적인 영향을 끼치는 색보간과 잡음 제거의 중요도가 가장 높다.

잡음 제거[3][4]는 영상의 윤곽선을 유지하면서도 잡음만을 효과적으로 제거하는 속성이 필요한데, 이를 위해서는 주어진 화소가 잡음인지 신호인지를 구분해야 한다. 따라서 잡음 제거를 비롯하여 유효한 영상 처리와 분석을 위해서 잡음의 양을 추정하는 일의 중요성은 매우 크다. 추정된 잡음의 크기는 잡음과 신호를 구분하기 위한 문턱치로 사용될 수 있기 때문에, 알고리즘들이 적응적으로 동작하도록 이끌어준다. 잡음이 포함된 영상 Y (m,n) 은 다음과 같이 백색잡음이 가산된 것으로 모델링된다.

식 (1)에서 (i, j) 는 영상에서 필터링하려는 화소의 현재 위치를 나타내는데, i 와 j 는 각각 수평, 수직방향의 위치를 나타내는 독립변수이다. X (i, j)는 (i, j) 에서의 이상적인 영상의 밝기값을 나타내고, N (i, j) 은 표준편차가 σ_n 인 가우시안 분포를 따르는 백색잡음이다.

Immerkaer는 3×3 커널만을 사용해서 잡음의 크기를 제안하는 계산효율적인 알고리즘을 제안했다[5]. 이 알고리즘은 잡음이 클수록 추정오차가 줄어들지만, 잡음의 절대값이 작을 경우에는 추정오차가 매우 크다는 것이 단점이다. 이는 영상의 윤곽선 근처와 같이 밝기값의 변화량이 잡음에 비해서 상당히 큰 경우에도 잡음 연산에 포함시킴으로써 잡음이 적을 경우에는 영상의 속성에 따라서 추정 오차가 커지는 현상을 보이게 된다.

Tae & Yang은 윤곽선을 감지하여 평탄한 영역만을 고려하여 잡음의 크기를 추정함으로써 진일보된 성능 향상을 보여준다[6]. 윤곽선 측정 단계가 추가될 경우에는, 윤곽선 여부를 판단하기 위한 기준이 필요한 데, 이 기준이 잡음의 크기에 따라서 달라지기 때문에 재귀적 연산의 필요성을 가지고 있다. Kim & Oh는 소벨(Sobel) 필터와 형태론적 필터를 이용하여 윤곽선을 추정하는 방법을 적용하여, 개선된 결과를 도출하기는 했으나, 기존 알고리즘의 구조로부터 주목할 만큼 개선된 부분은 없다[7].

기존 방법들은 잡음이 클 경우에는 추정 오차가 작지만, 잡음이 작은 경우에는 추정 오차가 큰 폭으로 증가하는 단점을 가지고 있다. 일반적인 영상에서 나타나는 잡음의 표준편차는 4~10의 사이에 있게 되는데, 이 범위의 백색잡음에 대해서 기존 방법들의 추정 오차는 20%를 크게 상회하기 때문에 보완이 필요하다.

본 논문에서는 각 화소 위치에서 백색잡음의 성향이 높은지를 판단하여, 3×3 커널에서 2개의 화소 데이터를 취한다. 이 화소 데이터들은 영상 신호와 잡음이 합해진 형태이므로, 이들 간의 차이값은 순수한 잡음 성분이 된다. 이렇게 영상 전체에서 취합한 잡음 데이터를 이용하여 잡음의 표준편차를 추정하는 방식을 제안한다. 본 논문의 구성은 다음과 같다. 2장에서는 기존 방법을 소개하고, 3장에서 제안한 방법을 제시한다. 4장에서 제안한 방식의 성능을 분석하고, 5장에서 결론을 내린다.

Ⅱ. 백색잡음 추정 방식

2.1 라플라시안(Laplacian) 커널을 이용한 잡음추정[4]

영상에 윤곽선과 같은 데이터 형태는 2차 미분값을 크게 만들기 때문에, 잡음 추정 알고리즘은 영상의 라플라시안에 둔감하도록 만들어져야 한다. 그림 1(a)에 2개의 3×3 라플라시안 커널을 각각 L₁, L₂로 정의하여 도시했고, 잡음 추정을 위한 커널 N은 2(L₂-L₁)으로 정의하여 그림 1(b)에 나타냈다.

커널 N으로부터 출력 데이터의 평균은 0이며, 분산은 36σn²이 된다. 따라서 잡음의 분산 σn²는 식 (2)에 의해서 구할 수 있다. 식 (2)에서 W는 영상의 수평 해상도, H는 수직해상도를 나타내며 *는 컨볼루션 연산을 나타낸다.

Fig. 1.

(a) 3x3 Laplacian kernel L1 , L2 , (b) 3x3 noise estimation kernel N = 2(L2 - L1)

$\[ {\sigma }_n^2=\frac{1}{36\left(W-2\right)\left(H-2\right)}\sum _{\left(i, j\right)}{\left({Y\left(i, j\right)}^{*}N\right)}^2 \]$

(2)

식 (2)는 매 화소위치에서 제곱 연산을 수행하는데, 식 (3)과 같이 절대값 연산으로 변경하더라도 연산결과는 차이가 없다.

$\[ {\sigma }_n^2=\sqrt{\frac{\pi }{2}}\frac{1}{6\left(W-2\right)\left(H-2\right)}\sum _{\left(i, j\right)}\left|{Y\left(i, j\right)}^{*}N\right| \]$

(3)

2.2 윤곽선 검출과 라플라시안 커널을 이용한 잡음 추정[5]

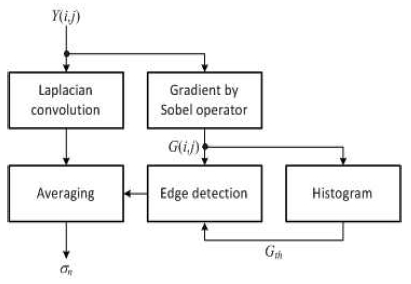
이 방법에서는 윤곽선이 아닌 데이터들에 대해서만 식 (3)을 적용해서 잡음의 크기를 구함으로서 영상의 내용에 대한 의존도를 낮춘다. 전체 처리 과정은 그림 2에 도시되어있다. 그림에서 '라플라시안 컨벌루션'은 그림 1(c)에 의한 컨볼루션을 나타내고, '에버리징(Averaging)'은 식 (3)을 계산하기 위해서 누적합과 평균을 구하는 과정이다.

Fig. 2.

Noise estimation using edge detection

윤곽선이 아닌 화소에 대해서만 라플라시안 컨벌루션을 적용해야 하므로, 각 화소에 대해서 윤곽선 여부를 판단해야 한다. 이를 위해서 식 (4)의 소벨 연산자[5]를 통해서 그래디언트 영상 G (i, j) 를 만든다.

$\[ G_x={Y\left(i, j\right)}^{*}\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\right] \]$

(4)

$\[ G_y={Y\left(i, j\right)}^{*}\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right] \]$

$\[ G=\left|G_x\right|+\left|G_y\right| \]$

그래디언트 영상의 각 화소가 문턱치 G_th보다 크면 1, 그렇지 않으면 0으로 하여 윤곽선 마스크를 만든다. 윤곽선 마스크를 가지고 현재 화소를 중심으로 5×5 커널을 구성하고, 그 합이 T보다 크면 해당 화소를 윤곽선 데이터로 확정한다. 윤곽선이 아닌 데이터에 대해서만 식 (3)을 적용하여 잡음의 크기를 계산한다.

문턱치 G_th는 그래디언트 영상 G (i, j) 의 히스토그램으로부터 계산한다. 0부터 히스토그램을 누적시킨 값이 전체 영상의 p%에 이르도록 만들 때의 그래디언트값을 G_th으로 결정한다. 실험적으로 p=10을 사용하지만, G_th는 영상의 복잡도나 잡음의 크기에 따라 가변적으로 결정된다.

Ⅲ. 백색잡음 테스트를 통한 잡음 추정

3.1 잡음 추정 방식 개요

제안한 방법은 라플라시안 커널을 이용하여 잡음의 분산을 계산하지 않고, 입력 영상으로부터 잡음을 대변하는 데이터를 선별하여 이들로부터 잡음의 크기를 계산한다. 전체 처리과정은 그림 3과 같다.

Fig. 3.

Noise estimation through white noise test

관측된 영상 데이터는 신호와 잡음의 합으로 표현된다. 따라서 신호의 변화량이 없는 영역에서 변화량은 잡음에 의해서 결정되기 때문에, 신호의 변화량이 적은 영역에서는 잡음 추정을 위한 표본을 취하기에 바람직하다. 현재 화소 위치 (i, j) 에서의 영상 데이터 Y (i, j) 가 다음 절에 기술된 백색잡음 테스트를 통과할 경우 수평방향의 그래디언트 Y (i - 1, j) - Y (i + 1, j)에 대해서 분산을 계산한 후, 이로부터 잡음의 분산을 식 (5)와 같이 계산한다.

$\[ E\left[{\left(Y\left(i-1, j\right)-Y\left(i+1, j\right)\right)}^{2 }\right] \]$

(5)

$\[ =E\left[{Y\left(i-1, j\right)}^2\right]+E\left[{Y\left(i+1, j\right)}^2\right]-2E\left[Y\left(i-1, j\right) Y\left(i+1, j\right)\right] \]$

$\[ ={\sigma }_X^2+{\sigma }_n^2+{\sigma }_X^2+{\sigma }_n^2-{2\sigma }_X^2={2\sigma }_n^2 \]$

식 (5)에서는 수평방향의 그래디언트에 대한 분산을 구했으나, 수직방향이나 대각선방향의 그래디언트에 대해서 분산을 구하더라도 상관없다. 그럼에도 불구하고 수평방향의 그래디언트를 선택한 것은 계산의 용이함 때문이다.

Ⅳ. 제안한 방식의 성능 분석

4.1 성능 평가를 위한 영상

성능 평가를 위해서 50종의 512×512 표준 영상[8]을 사용한다. 그림 4는 50종의 영상 중에서 순서대로 9개를 보여준다.

Fig. 4.

Test images

테스트 영상은 0~255사이의 값을 가지고 있기 때문에, 잡음을 추가한 후에도 0~255사이의 값을 가지도록 제한했다. 이런 제한을 가하면 더해지는 잡음의 크기가 다소 줄어드는 효과가 나타나서, 추가된 잡음에 대해서 표준편차를 구하면 의도한 것보다 약간 작은 값이 된다. 표 1은 테스트 영상에 대해서 분산의 크기가 2~12인 백색잡음을 평가 영상에서 더한 후, 기존의 방법들과 제안한 방법으로 추정한 잡음 크기를 평균한 것이다. 표1의 첫 번째 열에는 실제로 영상에 추가된 잡음의 실제 크기를 나타낸다.

Table 1.

Noise estimation results

성능 비교를 위한 수단으로 추정비율(Estimation Ratio)[5]를 사용하며, 이는 다음과 같이 정의된다. 표 2는 3가지 방식에 대한 추정비율을 나타낸다.

Table 2.

Comparison of noise estimation ratios

$\[ estimation ratio=\frac{{\sigma }_{estimated}}{{\sigma }_{added}} \]$

(7)

표 2에 의하면 제안한 방법은 기존방법보다 이상적인 추정비율인 100%에 근접하는 것을 확인할 수 있다. 특히, 백색잡음의 표준편차의 범위가 4~10일 때, 제안한 방법의 평균 예측 오류는 8.38%이었으며, 이는 기존방법의 52.01%나 23.91%로부터 큰 폭으로 개선된 것이다. 그림 5는 표 2의 결과를 도식적으로 나타낸 것이다.

Fig. 5.

Comparison of noise estimation ratios

Ⅴ. 결 론

영상에서의 잡음 제거는 압축 효율을 향상시키고, 주관적 화질 개선을 위해서 필수적인 단계이다. 잡음 제거는 잡음이 클수록 더 큰 커널을 사용하거나, 잡음과 신호를 구분하기 위한 문턱치를 조절함으로써 능동적으로 잡음 제거 필터의 구조가 변하는 것이 바람직하다. 본 논문에서는 백색잡음 테스트를 통과한 데이터를 기반으로 잡음의 크기를 계산하는 방법을 제안했다. 백색잡음의 표준편차의 범위가 4~10일 때, 제안한 방법의 평균 예측 오류는 8.38%이었으며, 이는 기존방법의 52.01%나 23.91%로부터 큰 폭으로 개선된 것이다. 제안한 방법은 하드웨어 구현에 적합한 구조를 가졌기 때문에, 성능향상을 도모하기 위하여 잡음 제거 필터에 내장되는 것이 가능하다.

References

• Bryce E. Bayer, "Color imaging array", US patent 3971065, July), (1976.
• C. M. Kyung, "Theory and applications of smart cameras", Springer, p21-45, Jul), (2014.
• Hyun-Sang Park, "Efficient Hardware Architecture of Bilateral Filter Using Approximate Computing Technique", Journal of KIIT, 15(9), p49-55, Sep), (2017. [https://doi.org/10.14801/jkiit.2017.15.9.49]
• K. He, J. Sun, and X. Tang, "Guided image filtering", IEEE Trans. on Pattern Analysis and Machine Intelligence, 35(6), p1397-1409, Jun), (2013.
• J. Immerkaer, "Fast noise variance estimation", Computer Vision and Image Understanding, 64(2), p300-302, Sep), (1996.
• S. C. Tai, and S. M. Yang, "A fast method for image noise estimation using Laplacian operator and adaptive edge detection", Proc. of IEEE International Symposium on Communications, Control and Signal Processing, p1077-1081, Mar), (2008.
• Y. R. Kim, and T. M. Oh, "Noise estimation using edge detection in moving pictures", Journal of the Institute of Electronics and Information Engineers, 52(4), p207-212, Apr), (2015. [https://doi.org/10.5573/ieie.2015.52.4.207]
• "Dataset of standard 512x512 grayscale test images", http://decsai.ugr.es/cvg/CG/base.htm [Accessed: Dec. 12. 2017].