다층신경망의 다양한 연결구조 제안 및 분석

Ⅰ. 서 론

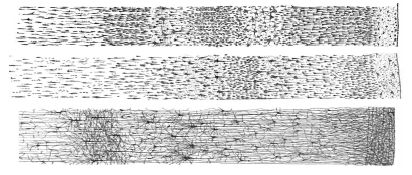
신경망(Neural Network)은 생물학적 뇌 구조와 동작을 모사한 계산모델이다. 뇌의 전기화학적 신경신호 전달물질과 전달경로를 통하여 학습시킴으로써 지능적으로 행동할 수 있도록 한다[1]. 뇌는 뉴런(Neuron)들 사이에 수많은 시냅스(Synaptic)가 복잡한 그물처럼 연결되어있다. 뉴런의 연결강도에 따라 연결구조가 변하는 것을 뇌 가소성(Neuro-Plasticity)이라한다. 뇌 가소성은 학습과 관계가 있다[2]-[4]. 생물학적 뇌는 그림 1과 같이 뉴런들 사이에 레이어의 구분이 없다. 또한, 각 레이어에 위치한 뉴런은 인접한 레이어의 뉴런들로만 연결되어 있지 않다. 하나의 뉴런에서 여러 가지 돌기(Dendrite)가 뻗어 나와 다른 뉴런으로 연결되는 복잡한 연결구조를 가진다.

Fig. 1.

Cajal cortex drawing

신경망은 주어진 학습을 통하여 스스로 지식을 획득한다. 가장 흔하게 사용하는 다층신경망(Multilayer Neural Network)은 여러 개의 레이어 즉, 층으로 구성된 전진전파(Feed Forward) 신경망이고 오류역전파(Backpropagation) 학습알고리즘을 사용한다.

다층신경망 네트워크는 입력레이어, 은닉레이어, 출력레이어로 구성되어있다. 각 레이어 내의 연결과 출력레이어에서 입력레이어로 직접적인 연결은 존재하지 않는 전진전파 네트워크이다. 오류역전파 알고리즘은 각 레이어의 뉴런과 뉴런 사이의 연결강도 값을 조정한다. 각 레이어의 연결강도 값은 편미분의 연쇄법칙(Chain Rule)[5]을 이용한다.

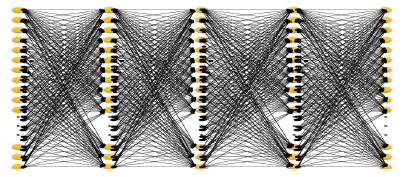
또한, 다층신경망은 그림 2와 같이 계산상의 편의성을 위하여 인접한 뉴런들과 연결되는 완전연결구조(Fully Connected)를 가지고 있다.

Fig. 2.

Neural network architecture of MLP model

다층신경망은 복잡한 비선형문제를 해결하기 위하여 층이 많은 깊은 레이어를 사용한다. 레이어가 깊어질수록, 가중치 수정량(Gradient)이 미분에 의해 빠른 속도로 수렴한다. 수렴 속도가 빠를 경우, 학습성능이 저하되는 문제(Vanishing Gradient)가 발생한다[6]. 또한 허용오차 부근이나 오차 곡선이 깊은 계곡 형태인 경우, 실제 데이터에 대한 오차가 커져 학습성능이 저하되는 문제(Overfitting)가 발생된다[7][8]. 그러나 학습된 신경망은 연결가중치에 오류가 생겨도 나름의 결과를 내놓는다[9].

본 논문에서는 입력신호가 네트워크 전체에 고르게 전달하기 위해 학습이 가능하고 인접하지 않은 레이어의 뉴런들과 연결이 허용되는 신경망 연결구조를 제안하고 분석한다. 2장에서 신경망의 연결구조 관련연구를 살펴본다. 3장과 4장에서는 제안한 연결구조를 알아보고 다층신경망과 비교하여 학습성능을 분석한다. 마지막 5장에서는 연구의 성과 및 향후 방향을 제시한다.

Ⅱ. 관련연구

연결구조에 따른 기존 연구에서, 은닉 뉴런간의 연결구조에 따른 시계열 학습과 동역학을 분석한 연구[10]와 ResNet(Residual Network)[11][12]이 있다. 동역학 분석 연구의 경우, ESN(Echo State Network)을 기준으로 네트워크 모델에 따라 은닉 뉴런간의 연결구조로 구성되어있다. ESN의 구성은 일반적인 RNN(Recurrent Neural Network)과 동일하다. RNN의 경우 시간에 따른 Recurrent 레이어가 동일한 가중치를 가지므로 학습의 대상이 아니다.

또한, 최근 가장 많이 연구되고 있는 ResNet은 CNN(Convolution Neural Network)을 기반으로 연결구조를 바꾼 경우이다. 일반적인 CNN은 입력 신호를 컨볼루션(Convolution) 레이어와 서브 샘플링(Subsampling) 레이어를 거쳐 출력을 내는 반면 ResNet은 출력 값과 입력 신호의 차이를 얻을 수 있도록 학습하게 된다. 즉, 입력 신호가 컨볼루션 레이어와 서브 샘플링 레이어를 건너뛰어 곧바로출력으로 연결되는 연결선을 생성한다. 그러나 이러한 연결선은 가중치의 변화 없이 전달되므로 일반적인 신경망 연결과는 다르다. 즉, 학습의 대상이 아니다.

본 연구에서는 모든 연결이 학습이 가능하고 입력신호를 네트워크 전체에 효과적으로 전달되는 연결 구조를 제안한다.

Ⅲ. 먼 레이어 뉴런의 연결을 허용하는 구조

입력신호를 신경망 네트워크 전체에 고르게 전달하기 위해 인접하지 않은 레이어의 뉴런들과도 연결이 허용되는 신경망 연결구조를 제안한다. 데이터는 표준으로 사용되는 MNIST(Modified National Institute of Standards and Technology database) 데이터셋과 HandWritten 데이터셋을 사용하였으며 제안한 깊이별 연결구조는 아래와 같다.

3.1 다양한 연결구조

제안한 연결구조는 다층신경망에 연결구조를 추가하여 구성하였다. 비교분석을 위하여, 기존 다층신경망을 SLA(Standard Link Architecture), 제안한 신경망 연결구조는 MLA(Modify Link Architecture)로 명명하였다. MLA 연결구조는 크게 두 가지로 분류하였다. 하나는 척도 없는 네트워크[12]-[15]의 허브(Hub)를 응용한 연결구조이다. 척도 없는 네트워크는 연결선수가 멱함수(Power Law)를 따르며 다수의 연결 수를 가진 허브가 존재하는 네트워크이다.

또 다른 하나는 뉴런 즉, 노드의 선택을 무작위 네트워크를 응용한 연결구조이다. 무작위 네트워크는 확률에 의해 연결선이 생성되는 통계학적 모델이다. 도수의 분포함수가 푸아송 분포를 따르는 Erdös-Rényi 모델이라고도 한다.

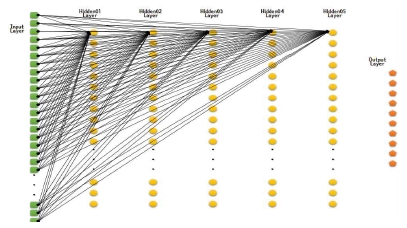
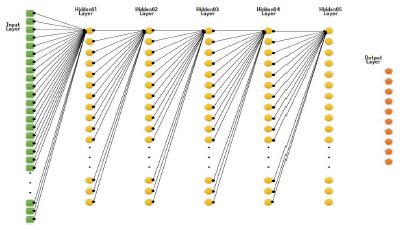
예를 들어, 입력과 출력레이어를 제외한 은닉레이어가 5개인 경우, SLA 연결구조를 제외한 제안한 다양한 MLA 연결구조는 다음과 같다.

• ● SMLA : SLA + 입력레이어로부터 각 은닉레이어의 첫 번째 노드에 연결
• ● SSMLA : SLA + 입력레이어로부터 다음 은닉레이어의 첫 번째 노드에 연결
• ● RMLA : SLA + 입력레이어로부터 다음 은닉레이어의 노드를 무작위로 선택한 연결
• ● RRMLA : SLA + 각 레이어로부터 다음 은닉레이어의 노드를 무작위로 선택한 연결

Fig. 3.

SMLA link architecture

Fig. 4.

SSMLA link architecture

Fig. 5.

RMLA link architecture

Fig. 6.

RRMLA link architecture

3.2 평가를 위한 문제 및 환경

제안한 연결구조의 성능을 분석하기 위한 데이터는 UCI Machine Learning Repository[16]의 Semeion Handwritten Digit Dataset[17]과 Gisette 데이터셋[18]을 비교분석하였다.

Semeion Handwritten Digit Dataset은 그레이스케일의 픽셀 16×16 경계상자를 사용하였다. 각 픽셀은 고정된 임계값을 사용하여 부울(0/1)값으로 스케일링되었다.

Gisette 데이터셋은 MNIST 데이터셋이라고도 불리며 다양한 이미지 처리 시스템을 교육하기 위해 일반적으로 사용되는 필기 자릿수 데이터베이스이다[19][20]. MNIST 데이터베이스는 기계 학습 분야의 교육 및 테스트에도 널리 사용되고 있다[21]. 또한, 그림 7과 같이 MNIST 흑백이미지는 픽셀 28x28 경계상자에 이미지 가장자리를 부드럽게 처리하는 안티앨리어싱(Aanti-aliased)으로 정규화되어 있다.

Fig. 7.

MNIST data example

연결구조의 입력은 각 숫자 이미지의 픽셀 값들의 벡터로 주어지고 출력은 0부터 9까지 10개의 숫자를 인식하는 문제이다. 각각의 훈련 데이터는 HandWritten 데이터셋은 1593개를 사용하였으며 테스트 데이터는 100개의 데이터를 사용하여 분석하였다. MNIST 데이터셋는 대용량의 데이터베이스로 60,000개를 사용하였으며 테스트 데이터는 10,000개의 데이터를 사용하였다. 각 깊이별 학습성능이 저하되는 문제를 분석하기 위하여 SLA와 MLA 연결구조를 학습률(Learning Rate), 모멘텀(Alpha)을 다양하게 바꾸어 10회 테스트의 평균으로 분석하였다.

레이어가 깊어질수록 학습성능이 저하되는 문제를 분석하기 위하여 은닉레이어를 다양하게 실험하여 보았다. 일반적으로, MNIST 데이터셋을 사용한 모델에서 학습성능이 유지되는 경우는 6인 레이어까지 사용한 경우이다[22]. 제안한 연결구조의 학습성능을 실험하기 위하여 은닉레이어를 5부터 10까지 깊이별로 분석하였다.

또한, 실제 데이터에 대한 오차가 커져 학습성능이 저하되는 문제를 개선하기 위해 훈련 데이터와 테스트 데이터를 달리하여 분석하였다.

Ⅳ. 연결구조 학습성능 분석

제안한 MLA 연결구조는 기존 다층신경망 연결구조(SLA 연결구조)에 추가된 가중치 연결로 이루어져있다. 각 연결구조는 은닉레이어의 개수별 평균학습성능과 평균 학습속도를 비교분석하였다. 비교분석을 위하여 RMLA, RRMLA, SLA, SMLA, SSMLA 연결구조순으로 열거하였으며 은닉레이어는 레이어 5부터 10까지로 나누어 깊이별 평균 학습성능과 평균 학습속도를 실험하였다.

4.1 데이터셋에 따른 깊이별 학습성능

기존 다층신경망인 SLA 연결구조와 제안한 연결구조들의 데이터셋을 달리하여 보았다. 제안한 연결구조들의 HandWritten, MNIST 데이터셋의 깊이별 학습성능과의 관계를 알아보았다.

표 1은 HandWritten 데이터셋에서 은닉레이어의 깊이가 5인 경우에서 은닉레이어 10인 경우의 평균 학습성능을 비교하여보았다. SLA 연결구조의 경우 44.1%를 보였으며 RMLA 연결구조의 경우 레이어가 94.5%의 높은 학습성능 평균을 보였다.

Table 1.

HandWritten, average learning performance for each layer

표 2는 MNIST 데이터셋에서 은닉레이어의 깊이가 5인 경우에서 은닉레이어 10인 경우의 평균 학습성능을 비교하여보았다. SLA 연결구조의 경우 52.0%를 보였으며 RRMLA 연결구조의 경우 레이어가 88.3%의 높은 학습성능 평균을 보였다.

Table 2.

MNIST, average learning performance for each layer

그림 8과 그림 9를 살펴보면 레이어가 깊어질수록 기존 다층신경망인 SLA 연결구조는 학습성능이 현저하게 떨어진다. 반면, 제안한 연결구조의 경우 학습성능이 완만한 연결구조를 보이고 있다.

Fig. 8.

HandWritten, average learning performance change by each layer

Fig. 9.

MNIST, average learning performance change by each layer

특히, 입력신호가 네트워크 전체에 고르게 전달되기 위해 학습이 가능하고 인접하지 않은 레이어의 뉴런들과도 연결이 허용되는 신경망 연결구조 중 RMLA 연결구조는 HandWritten, MNIST 데이터셋모두 우수한 학습성능을 보였다.

4.2 데이터셋에 따른 깊이별 SLA와 RMLA 학습성능

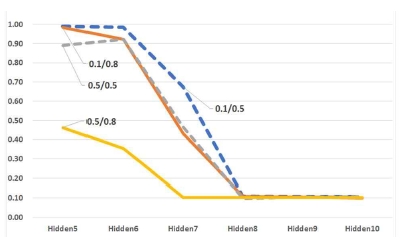
데이터에 따른 깊이별 학습성능 분석결과, 기존 다층신경망 SLA 연결구조와 비교하여 데이터셋을 달리한 경우 RMLA 연결구조가 모두 우수한 학습성능을 보였다. 이를 토대로 HandWritten, MNIST 데이터셋의 매개변수 학습률을 0.1/0.5로 차이를 크게 하여 실험하였으며, 모멘텀(Alpha)은 0.5/0.8로 달리하여 은닉레이어 깊이별 학습성능을 알아보았다.

표 3과 표 4에서 보면 HandWritten 데이터셋의 SLA 연결구조는 은닉레이어의 깊이가 깊어질수록 매개변수와 무관하게 현저하게 떨어지는 것을 알 수 있었다. 반면, RMLA 연결구조는 매개변수를 달리하여도 평균 학습성능과는 무관함을 보였다.

Table 3.

HandWritten_SLA, parameter and average learning performance for each layer

Fig. 10.

HandWritten_SLA, parameter and average learning performance

Table 4.

HandWriten_RMLA, parameter and average learning performance

Fig. 11.

HandWritten_RMLA, parameter and average learning performance

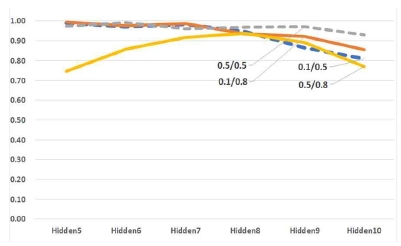
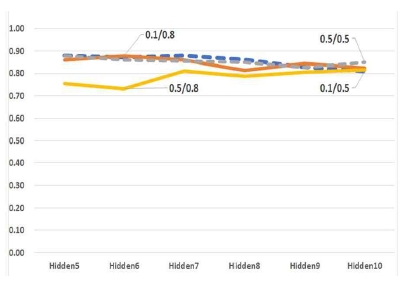
표 5와 표 6에서 보면 HandWritten 데이터셋과 유사하게 MNIST 데이터셋의 SLA 연결구조는 은닉레이어의 깊이가 깊어질수록 매개변수와 무관하게 현저하게 떨어지는 것을 알 수 있었다. 반면, RMLA 연결구조는 매개변수를 달리하여도 평균 학습성능과는 무관함을 보였다.

Table 5.

MNIST_SLA, Parameter and Average learning performance

Fig. 12.

MNIST_SLA, parameter and average learning performance

Table 6.

MNIST_RMLA, parameter and average learning performance

Fig. 13.

MNIST_RMLA, parameter and average learning performance

4.3 가중치 연결 수에 따른 학습속도

제안한 연결구조는 SLA 연결구조에 추가된 가중치 연결로 이루어져있다. MNIST 데이터셋의 경우 입력신호가 28×28(784개)의 입력신호를 가지므로 연결구조에 따라 추가된 연결선의 수는 많아지게 된다. MNIST 데이터셋에서 SLA 연결구조를 기준으로 추가된 연결 수와 학습속도 관계를 알아보았다.

표 7은 SLA 연결구조를 기준으로 각 레이어 깊이별 제안한 연결구조의 연결선 수를 나타낸다. 각 레이어별로 보면 SMLA 연결구조가 기존 SLA 연결구조에 비하여 많은 학습 연견선으로 표현된다.

Table 7.

Average weighted link for each layer

표 8은 가중치 연결 수에 따른 학습 완료시간을 초(Second) 단위로 비교하여 보았다.

Table 8.

Average learning performance timefor each layer

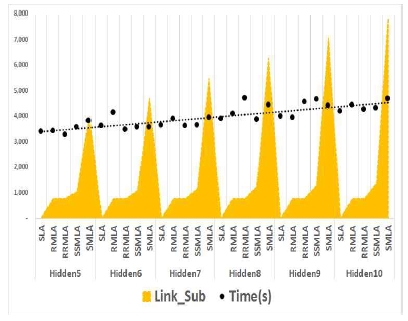
그림 14는 제안한 MLA 연결구조의 가중치 연결 수에 따른 각 깊이별 추가된 연결 수(Link_Sub)와 학습속도(Time(s))의 관계를 나타낸다. 레이어가 깊어질수록 SLA를 기준으로 가중치 연결 수는 각 연결구조에 따라 증가하게 된다. 반면, 각 깊이별로 학습속도는 증가된 가중치 연결 수에 비하여 일정한 분포를 이루고 있다. 학습속도면에서, 추가된 연결 수는 기존 다층신경망의 학습속도와 무관하였다.

Fig. 14.

Number of weight connections and learning speed for each layer

4.4 가중치 연결 수에 따른 학습성능

SLA 연결구조와 제안한 MLA 연결구조들의 평균 학습성능을 실험하였다. 먼저, 추가된 가중치 연결수와 학습성능의 관계를 알아보았다. 특히, 레이어의 깊이와 학습성능의 관계를 확인하기 위해 레이어 깊이를 다르게 하여 분석하였다.

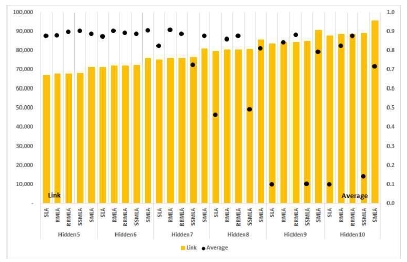
그림 15는 제안한 MLA 연결구조의 가중치 연결 수에 따른 각 깊이별 연결 수(Link)와 학습성능(Average)의 관계를 나타낸다. SLA 연결구조의 경우, 은닉레이어가 8부터 급격하게 학습성능이 떨어진다. 반면, RMLA와 RRMLA 연결구조는 레이어가 깊어져도 추가된 가중치 연결 수에 비해 학습성능이 떨어지지 않았다.

Fig. 15.

Number of weighted connections and learning performance for each layer

실험결과, 다층신경망에 가중치 연결수를 추가하더라도 학습속도와는 무관하였다. 또한, 가중치 연결을 무작위로 추가한 경우 레이어가 깊어져도 학습성능에 변화를 주지 않았다.

Ⅴ. 결론 및 향후 과제

본 논문에서는 입력신호를 네트워크 전체에 고르게 전달하기 위해 학습이 가능하고 인접하지 않은 레이어의 뉴런들이 서로 연결될 수 있는 신경망 연결구조를 제안하고 분석하였다.

제안한 다양한 연결구조는 기존 다층신경망에(상대적으로 극히 적은) 연결을 추가한 것이다. 학습속도와 학습성능을 분석한 결과 제안한 연결구조는 기존 다층 신경망에 견주어 레이어가 깊어져도 학습속도와 무관하였다. 또한, 가중치 연결을 무작위로 연결한 경우 레이어가 깊어져도 우수한 학습성능을 유지하였다.

본 논문에서는 기존 다층신경망의 학습성능을 높이기 위해 신경망의 추가된 연결구조가 학습성능에 영향을 미칠 수 있다는 점에 의의를 찾아볼 수 있다. 추후, 다양한 활성함수를 사용하여 성능을 분석하고 특히 기울기 소실 문제를 심도 있게 분석할 것이다. 또한, 딥러닝을 위한 다양한 데이터와 신경망 연결구조에 적용해 볼 것이다.

References

• Sung-Kwun Oh, "Computational Intelligence by Programming focused on Fuzzy, Neural Networks, and Genetic Algorithms", Naeha Press, p225, Aug), (2002.
• J. T. Wall, J. Xu, and X. Wang, "Human brain plasticity: an emerging view of the multiple substrates and mechanisms that cause cortical changes and related sensory dysfunctions after injuries of sensory inputs from the body", Brain Research Reviews, 39(2-3), p181-215, Sep), (2002. [https://doi.org/10.1016/s0165-0173(02)00192-3]
• R. G. Coss, J. G. Brandon, and Globus Albert, "Changes in morphology of dendritic spines on honeybee calycal interneurons associated with cumulative nursing and foraging experiences", Brain Research, 192(1), p49-59, Jun), (1980. [https://doi.org/10.1016/0006-8993(80)91007-0]
• F. H. Gage, "Structural plasticity: cause, result, or correlate of depression", Biol Psychiatry, 48(8), p713-714, Nov), (2000. [https://doi.org/10.1016/s0006-3223(00)01019-2]
• Robert G. Bartle, and Donald R. Sherbert, "Introduction to REAL ANALYSIS", John Wiley & Sons, Inc., p208, (2006).
• E. K. Blum, "Approximation of Boolen Functions By Sigmoidal Networks: Part Ⅰ: XOR and other two-variable functions", Neural Computation, 1(4), p532-540, Winter (1989). [https://doi.org/10.1162/neco.1989.1.4.532]
• M. K. Weir, "A Method for Self-Determination of Adaptive Learning Rates in Back Propagation", Neural Networks, Pergamon Press, 4(3), p371-379, Dec), (1991. [https://doi.org/10.1016/0893-6080(91)90073-e]
• Mohandes, M., Codrington, CW., and Gelfand, S.B., "Two Adaptive Stepsize Rules for Gradient Descent and their Application to the Training of Feedforward Artificial Neural Networks", Proceedings of IEEE International Conference on Neural Network, p555-560, Jul), (1994. [https://doi.org/10.1109/icnn.1994.374225]
• Tae-Won Kang, "Fault Tolerance Analysis of the Neural Networks of Scale-Free Network Architecture", JKIIT, 11(7), p151--157, Jul), (2013. [https://doi.org/10.14801/kiitr.2013.11.7.151]
• M. Faloutsos, P. Faloutsos, and C. Faloutsos, "On power-law relationships of the internet topology", Computer Communications Review 29, p251-262, Sep), (1999.
• Sangwoong Yoon, and Byung-Tak Zhang, "Analyzing Performance and Dynamics of Echo State Networks Given Various Structures of Hidden Neuron Connections", KIISE Transactions on Computing Practices, 21(4), p338-342, Apr), (2015.
• Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun., "Deep residual learning for image recognition", arXiv preprint arXiv:1512.03385, (2015b).
• Mark Buchanan, "Ubiquity: the science of history. or why the world is simpler than we think", Amazon, (2001).
• D. J. Watts, "Small world: the dynamics of networks between order and randomness", Princeton, (1999).
• M. E. J. Newman, "Power laws, Pareto distributions and Zipf's law", Contemporary Physics, 46(5), p323-351, Sep), (2005. [https://doi.org/10.1080/00107510500052444]
• UCI Machine Learning Repository, http://archive.ics.uci.edu/ml/index.php [Accessed: Jan. 10. 2018].
• Semeion Handwritten Digit Dataset, https://archive.ics.uci.edu/ml/datasets/semeion+handwritten+digit [Accessed: Jan. 10. 2018].
• Gisette Dataset, https://archive.ics.uci.edu/ml/datasets/Gisette [Accessed: Jan. 10. 2018].
• X. Zhang, and J. Zhou, "Support vector machines speed pattern recognition - Vision Systems Design", Vision Systems Design, Aug, 17.), (2013.
• S. Gangaputra, "Handwritten digit database", Retrieved 17, Aug. 2013.
• Q. Yu, "THE MNIST DATABASE of handwritten digits", Retrieved 18, Aug. 2013.
• MNIST database Error Rates, https://en.wikipedia.org/wiki/MNIST_database [Accessed: Oct. 5. 2017].