기계학습을 활용한 항공기 연료 시스템 무결성 감시
*순천향대학교 전기통신시스템공학과**순천향대학교 전기공학과 조교수
초록
항공기 연료 시스템은 핵심적인 항공기의 전자, 기계적 시스템 중 하나로서 안전한 비행을 위해 연료 시스템의 신뢰성은 무엇보다 중요하지만, 현대의 항공기는 최첨단 기술과 장비의 탑재에도 불구하고 단순 결함 및 조종사 또는 정비사의 부주의만으로도 여전히 많은 사고가 발생하고 있다. 이에, 본 논문에서는 높은 신뢰성이 보장되어야 하는 항공기 연료 시스템의 오류로 인한 사고 발생을 사전에 방지하기 위해 항공기 연료 소모량 예측을 통한 무결성 감시 기법을 제안하였다. 신경망을 기반으로 한 항공기 연료 소모량 예측 알고리즘은 Levenberg Marquardt을 기반으로 학습하였으며, B747 항공기 데이터를 활용한 모의시험을 통해 기존 항공기 연료 소모량 모델과 비교 평가하였다. 그 결과, 간섭 노드(속도, 고도)와 무관하게 제안된 잡음 환경의 모의시험에서 예측 시스템은 기존 모델 대비 전 구간에 걸쳐 20~30% 이상 높은 잡음 강인성을 확인할 수 있었다.
Abstract
Aircraft fuel systems are one of the core electronic and mechanical systems of aircraft and the reliability of the fuel system for safe flight is of paramount importance. Despite the use of advanced technology and equipment, however, modern aircraft fuel systems still have vulnerabilities due to simple faults or crew carelessness. In this paper, we proposed an integrity monitoring method that uses an aircraft fuel consumption prediction algorithm to prevent accidents caused by aircraft fuel system errors that require high reliability and accuracy. The proposed aircraft fuel consumption prediction algorithm trained by the Levenberg-Marquardt learning method could confirm 20~30% higher robustness and superiority against the external environmental noise compared with the conventional aircraft fuel consumption model in the simulation using the B747-100 aircraft data.
Keywords:
aircraft fuel system, machine learning, neural networks, levenberg-marquadt methodⅠ. 서 론
1903년 라이트 형제가 첫 비행을 성공한 이래로, 지난 100년간 항공 산업은 폭발적인 발전을 거듭해오며 초소형 무인기, 초음속 비행을 하는 대형 항공기, 스텔스 기능을 탑재한 전투기 등 다양한 항공기의 연구 및 개발이 점차 가속화되어왔다. 특히, 항공운송 산업의 경우 전 세계 시장에서 기술적, 산업적, 경제적으로 눈부신 성장을 이뤄내며 현대사회를 지탱하는 중추적 이동 및 운송수단으로 자리 잡고있다[1]. 향후 20년간 항공 교통량이 현재의 2배 이상 증가할 것으로 예측되는 가운데, 무한 경쟁 속의 항공사들은 안전성과 신뢰성을 기반으로 하는 효율적인 항공기 운용을 위해 노력 중이지만 증가하는 항공 교통량 및 연료의 가격 상승 문제와 국제 환경 정책으로 인한 압박으로 어려움을 겪고 있다[2][3]. 이와 더불어, 최첨단 기술력과 장비의 탑재에도 불구하고 지속해서 발생하는 항공기 안전사고는 연쇄적인 물적 손해를 입히며 항공 운송 산업 성장에 제동을 가하고 있다. 비록 항공기의 안전사고는 1970년대 이후 점차 감소하여 전체 항공기의 비행횟수를 고려했을 때, 2016년 기준 100만 비행당 사상자 발생 및 기체 손상 사고의 발생 비율은 각 0.25%와 0.64%로 현저히 낮지만, 항공 교통량의 비약적인 증가로 여전히 매년 백여 건이 넘는 항공기 안전사고가 발생한다[4]. 표 1은 최근 5년간 발생한 항공기 안전사고와 사고로 인한 사상자 수를 나타낸다.
항공기 안전사고의 원인을 큰 범주에서 살펴보면 조종 과실과 기계적 결함이 전체 사고의 70% 이상을 차지하며 구체적으로는 불시착, 장비 고장, 조종실수, 정비 과실, 연료 고갈 등으로 분류된다[5]. 특히, 사고 발생의 원인 중 연료와 관련된 사고의 경우 치명적인 기계적 결함으로 인한 사고뿐만 아닌 단순 기계 오작동 또는 조종사나 정비사의 부주의로 인한 사고 발생 가능성이 존재한다.
2016년 11월 28일 콜롬비아에 추락하여 탑승자 77명 중 71명의 사상자를 낸 LMI 2933기의 사고 원인은 단순 연료 시스템의 전기적 결함으로 인한 연료 고갈 문제였으며, 2005년 8월 6일 이탈리아에 추락하여 39명 중 16명의 사상자가 발생한 TUX 1153기의 사고 원인은 단순 연료 게이지 이상과 연료 잔량 미확인으로 인한 사고였다. (그림 1 참조)
항공기 연료 시스템은 엔진과 보조 전력 계통에 안정적으로 연료를 공급하고 비행 고도 및 속도 등에 따라 최적의 양과 압력의 연료를 지속해서 유지해야 하는 항공기의 핵심적인 전자, 기계적 시스템 중 하나로서 항공기 연료 시스템의 신뢰성은 무엇보다 중요하다. 하지만 최첨단 기술력과 장비의 탑재에도 단순 결함 및 조종사나 정비사의 부주의만으로도 수많은 인명피해를 동반한 LMI 2933기와 TUX 1153기 사고와 같은 재난으로 연결되므로, 항공기 연료 시스템은 높은 정확성과 신뢰성을 갖춘 연료소모량 감시 시스템의 추가 탑재를 통해 이상 여부 감지가 요구된다.
현재 연료 소모량 예측에 대표적으로 사용되는 수학적 항공기 연료 소모량 모델(AFBM, Aircraft Fuel Burn Model)은 표준화된 항공기 데이터를 기반으로 하여 효율적인 항공기의 운용을 위해 탑재되는 최적의 연료량을 계산하는 모델이다.
하지만 AFBM은 실제 비행 환경에서의 기상 상태, 탑재된 화물 및 연료량 등에 의한 미세 잡음, 항공로(상승, 순항, 하강), 내부 진동 및 항행 거리에 따른 경로 오차율 등의 다양한 변수가 고려되지 않은 모델로서, 4% 오차 내의 신뢰성을 보장하지만 실제 비행 환경에서는 비행경로 오차만으로도 10% 이상의 거리오차가 발생할 가능성이 존재한다[1][6][7]. 따라서 개별적인 항공기에 탑재되어 실시간 예측 모델로 활용될 경우, 예측 부정확성의 가능성으로 인해 항공기 연료 시스템의 신뢰성에 영향을 미치게 될 수 있다. 이에, 본 논문에서는 신뢰성이 보장되어야 할 항공기 연료 시스템의 이상 유무 판별을 통한 시스템 신뢰성 향상을 위한 항공기 연료 소모량 예측 시스템(AFCP, Aircraft Fuel Consumption Predictor)을 제안하였다. 연료 소모량 예측 시스템 구현을 위해 대표적인 비선형 학습 모델인 신경망(NN, Neural Networks)을 활용하였으며, 신경망의 최적화 학습을 위해 높은 예측 안정성을 갖는 Levenberg-Marquardt 학습 알고리즘을 적용하였다. 제안하는 예측 시스템은 현재 운항 중인 항공기의 실데이터 확보 및 활용에 어려움이 있어 Bela P. Collins가 제안한 Advanced Fuel Burn Model과 보잉사의 B747-100 항공기 모델을 기반으로 연료 소모에 영향을 미치는 주요 변수인 비행 속도와 고도, 그리고 두 변수에 의한 연료 소모량 데이터를 생성하여 이를 바탕으로 설계하였다[8].
AFCP를 포함한 제안된 항공기 연료 시스템의 무결성 감시의 구조는 그림 2와 같으며, 항공기 연료 시스템의 센서로부터 측정된 연료량과 제안된 AFCP로부터 예측된 연료의 소모량을 비교하여 항공기 연료 시스템의 이상 유무를 판단한다. 항공기 연료 시스템에 대한 무결성 감시를 기반으로 연료 시스템에서 발생 가능한 결함을 조종사가 사전에 인지 및 사고 예방을 통한 비행 신뢰성 향상을 목표로 하였다. 모의실험을 통한 성능평가 결과 항공기 연료 소모량 예측을 위해 최적 설계된 AFCP는 기존 AFBM과 동일한 성능을 확보하였으며, 실제 상황에서의 적합성 평가를 위해 잡음 대 성능비를 비교한 결과 AFBM 대비 외부 환경 잡음에 보다 높은 강인성을 보여 항공기 연료 시스템의 무결성 감시를 위한 실질적인 활용을 기대할 수 있었다.
Ⅱ. 항공기 연료 소모량 모델
신경망 학습에 사용될 항공기 연료 소모량 모델은 공기역학 및 엔진 특성과 에너지의 균형 관계를 바탕으로 Collins가 제안한 AFBM을 고려하였다. AFBM 모델은 현재까지 다양한 연구에서 활용되고 있으며 그 신뢰성이 4% 내외의 오차를 보장하여 높다 할 수 있다[9]. AFBM에서 고려된 항공기의 에너지 균형관계식은 물리적 변수를 통해 식 (1)과 같이 표현할 수 있다.
| (1) |
여기서, ET는 항공기의 추력 에너지, ED는 항력 에너지이며, ΔKE와 ΔPE는 운동 에너지와 위치 에너지의 변화량이다. 식 (1)의 에너지 균형관계식을 기반으로 항공기 추력 Fthrust를 정의하면 식 (2)와 같다.
| (2) |
여기서, d는 비행 구간의 거리, V[ft/sce]는 진대기 속도(True Airspeed), SW[ft2]는 항공기 날개의 면적이다. M = (Ma.Mb,Mc)는 마하 계수의 함수로서 비선형 양한 곡선의 형태를 보이는 무 차원 항력계수 CD의 함수로 나타낼 수 있다[7]. ρ는 고도에 따른 공기의 밀도이며 제안하는 시스템의 모델은 미국 표준 대기를 기준으로 한다. 식 (2)에서의 마하 계수 M은 항공기 항력 계수의 상수 Kn과 마하 계수의 비율인 Γn의 관계식으로 식 (3)과 같이 표현된다.
| (3) |
식 (2)에서 정의된 밀도 ρ는 36,089ft를 기준으로 나뉘는 고도 h의 관계식으로서 식 (4)와 같다.
| (4) |
항공기의 비행로(상승, 순항, 하강) 및 내부 운동으로 인한 항공기 추력의 변화는 AFBM에서 고려되지 않기 때문에 식 (2)를 간략화하면 식 (5)와 같이 정리할 수 있다. 최종적으로 AFBM에서 정의한 연료 소모량 함수 Fi를 기반으로 하여 식 (5)를 변환하면 연료 소모량 Wfuel은 식 (6)과 같다.
| (5) |
| (6) |
여기서, F = [F1,F2,F3]는 연료 소모량 상수 Cn과 엔진의 개수 N으로 구성되며 식 (7)과 같다.
| (7) |
Ⅲ. 신경망 기반의 항공기 연료 소모량 예측 시스템
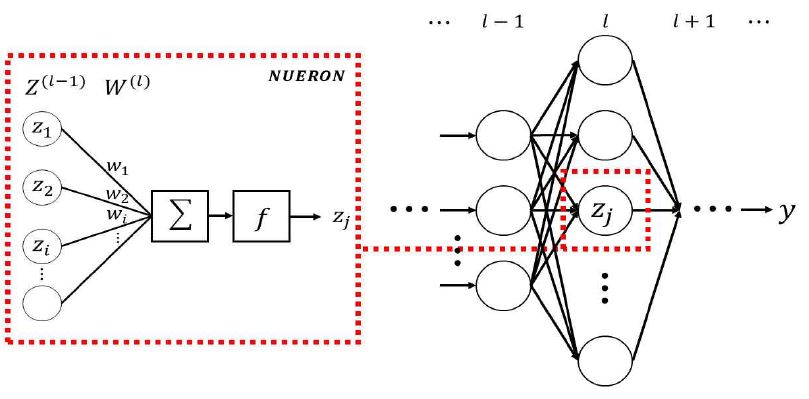
인간의 인식 과정과 신경의 생태를 수학적으로 모형화하여 영상처리, 음성인식, 패턴 분석 등에서 우수한 성능을 갖는 신경망(NN, Neural Networks)은 다양한 분야에서 지대한 관심을 받아오며 신경망을 기반으로 한 수많은 최적화 기법이 파생되고 있다[10]. 다양한 신경망의 형태 중 다층 퍼셉트론(MLP, Multi-Layer Perceptron) 구조는 비선형 문제해결에 뛰어나 일반적으로 사용되고 있으며, L개의 은닉층을 갖는 MLP를 고려할 경우 그림 3과 같이 표현할 수 있다[11].
그림 3에서 zi는 임의의 l층으로 전달되는 입력노드이며 wi는 입력 노드에 따른 가중치이다. zj는 신경망 내부 구조에 따라 전달되는 l층 j번째 노드의 출력으로서 합성함수의 식 (8)과 같다.
| (8) |
식 (8)에서 Z(l-1)은 zj와 연결된 zi의 전체 벡터, W(l)은 zj와 연결된 wi의 전체 벡터이다. h(·)는 임계 활성화 정도를 결정짓는 비선형 함수로서 다양한 함수의 형태 중 선형 포화함수를 미분 가능한 형태로 변형한 식 (9)의 시그모이드(Sigmoid) 함수를 사용한다.
| (9) |
MLP 구조의 신경망 내부 노드는 식 (8)의 합성 함수를 통해 다음 층으로 전달되며 단일 출력 노드를 고려할 때, 입력 데이터 집합 N의 k번째 데이터에 대한 신경망 입출력 관계식은 비선형 함수 f(·)의 식 (10)으로 정의된다.
| (10) |
여기서, W는 최종 출력에 대한 전체 가중치 벡터 W= [W(1),…,W(L)]T이며, X(k)는 전체 입력 노드의 벡터 X(k) = [x1,x2,…,xm]k로서, 이때 입력 노드의 개수는 m이라 가정한다. 신경망의 연결 강도를 최적으로 조절하기 위해 오차의 제곱 합이 최소가 되도록 가중치를 조정하는 최소 자승법(LS, Least Square)를 사용하였다. 학습의 기댓값과 오차를 t(k)와 rk= t(k) - y(k)의 관계식으로 정의하면 신경망의 출력과 기댓값에 대한 목적 함수 e는 식 (11)과 같다.
| (11) |
학습에 따라 반복적으로 갱신되는 임의의 횟수를 p라 할 때 데이터 집합의 전체 오차 값을 벡터로 표현하면 γp = [r(1),…,r(N)]T가 되며, p번 갱신된 가중치 Wp에 대한 목적 함수 E(·)는 식 (12)로 정의된다.
| (12) |
LS는 선형 시스템의 최적화 문제에서 가장 광범위하게 사용되지만, 비선형 시스템의 경우 점진적으로 해를 찾는 방법이 요구된다. 최적의 해를 찾기 위한 학습 알고리즘으로는 Gradient Descent, Gauss-Newton, Levenberg-Marquardt 방법 등이 있으며 이들 중 Levenberg-Marquardt 방법은 Gradient Descent와 Gauss-Newton 방법이 결합한 형태로 NN 비선형 학습에서 비교적 빠른 해의 수렴 속도와 뛰어난 예측 안정성을 강점으로 내세우며 다양한 분야에서 활용되고 있다[12][13]. 식 (12)의 목적 함수를 기반으로 Levenberg Maquardt 방법을 적용하면 p + 1 번째 학습된 가중치는 식 (13)과 같이 정의된다.
| (13) |
여기서, diag는 파라미터의 곡률을 나타내는 대각 행렬이며 ηq는 감쇠 상수로서 자코비안(Jacobian) 역행렬 계산에서 발생하는 발산 문제에 효과적이며 학습 정도에 따라 ηq의 갱신을 통해 NN 학습의 국부 극소점 문제에 대응할 수 있다. J는 W에 대한 자코비안 행렬로서 식 (14)와 같이 정의된다. JTJ의 역행렬은 근사화해 이차 미분 형태인 헤세(Hessian) 행렬 JT J ≈ ∇2E(Wp)로 표현된다.
| (14) |
Ⅳ. 항공기 연료 소모량 예측 시스템 성능 평가
제안하는 항공기 예측 시스템의 모의시험 데이터는 초대형 민간여객기로 장거리 국제선의 표준기종으로 되어있는 보잉 747 계열의 747-100 모델을 사용하였다. 표 2는 항공기의 연료 소모량을 도출하는데 필요한 B747-100 항공기의 파라미터와 실제 비행 환경에서 운용되는 범위를 나타낸 것이다[14].
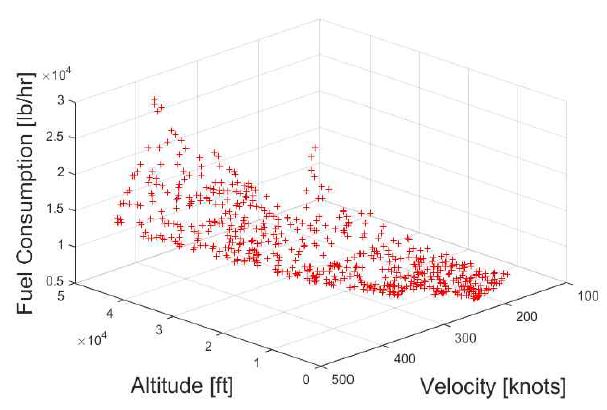
그림 4는 NN 학습을 위해 B747-100 항공기의 데이터를 기반으로 입력 데이터(속도, 고도)를 범위 내에서 무작위 생성한 뒤, 식 (6)의 Wfuel을 활용하여 도출한 출력 데이터(고도)를 3차원 그래프로 도식화한 것이다. 그림 5는 식 (13)의 Levenberg-Maquardt 방법을 기반으로 최적화될 AFCP의 내부구조이다.
본 논문에서 제안하는 Levenberg Marquardt 기반 예측 시스템(MLP/LM)은 평균 제곱 오차(MSE, Mean Square Error)를 활용하여 단층 구조(SLP, Single-Lyer Perceptron)의 예측 시스템과 일반적인 NN 학습에 활용되는 Gradient Descent를 기반으로 학습된 예측 시스템(MLP/GD)을 비교 평가하였다.
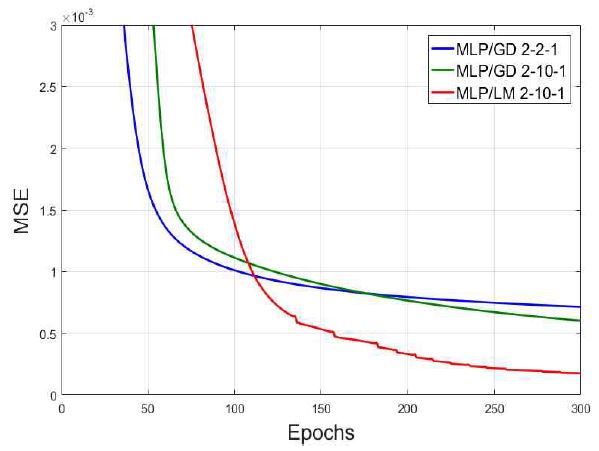
표 3은 50회의 몬테카를로 모의시험 결과의 MSE 평균을 나타낸 것으로, 학습 구조와 은닉층 노드에 임의의 변화를 주어 비교하였다. 학습 횟수는 300회, 초기 가중치 값은 ± 1 범위 내의 값으로 무작위 추출하여 적용하였다. 그림 6은 학습 횟수에 따른 각 예측 시스템의 MSE를 나타낸다.
예측 시스템의 구조에 따른 성능 평가 결과, 비선형 데이터 학습에 취약한 SLP는 예상한 바와 같이 MLP 구조와 비교하였을 때 상당히 저조한 예측력을 보였다. MLP/GD의 경우 은닉 노드 수의 증감과 관계없이 일정한 값으로 수렴하였으며, 제안하는 MLP/LM과 비교하였을 때 약 3배 이상 높은 MSE를 보여주었다. 이를 통해, AFCP의 예측 정확성을 검증할 수는 있지만 단순 예측력을 기준으로 AFBM과의 비교는 무리가 따른다. 제안하는 항공기 연료 소모량 예측 시스템은 수학적으로 정의된 연료 소모량 모델과 비교하여 높은 예측 정확성과 더불어 실제 비행하는 항공기 내·외부적으로 존재하는 불특정 잡음과 미세변수로 인한 비행 데이터의 손실 가능성을 고려해야 한다.
하지만 실제 항공기의 미세 변수에 의한 역학적 특성과 잡음은 비선형 특성이 강하며 일정하지 않고 환경에 따라 다양한 형태와 복잡성을 내재하여 성능평가를 위한 데이터 확보에는 어려움이 있다[15][16]. 이에 본 논문에서는 다양한 잡음 모델 중, 실제 환경에서 발생하는 잡음과의 유사성을 가지며 일반적인 잡음 강인성 평가에 활용되는 가우시안(Gaussian) 잡음 모델을 고려하였다[17].
| (15) |
잡음 모델은 식 (15)의 정규분포를 기반을 두며 상가성(Additive) 잡음 2.5~7.5% 범위의 간섭을 가정한 것으로서 식 (16)과 같으며, 잡음에 대응하는 강인성 평가를 위해 입력되는 데이터(속도, 고도)에 잡음모델을 적용하여 비교 시험평가를 수행하였다.
| (16) |
표 4는 최적 설계된 예측 시스템과 기존 수학적 모델의 잡음 강인성을 비교하기 위해 잡음의 강도와 잡음의 영향을 받는 간섭 노드(속도, 고도)를 구분하여 50회의 반복 시험 결과의 MSE를 평균으로 나타낸 것이다. 간섭노드에 따른 잡음의 민감도는 고도 데이터가 상대적으로 높게 나타났으며, AFCP는 간섭을 받는 노드와 무관하게 잡음의 간섭이 ϵ(2.5) 수준으로 낮을 경우 미세한 차이는 존재하지만. 전체적인 MSE는 대체로 AFBM과 유사한 수준임을 확인할 수 있었다.
하지만 잡음의 간섭이 ϵ(5.0) 수준으로 증가할 경우 간섭 노드에 따라 MSE는 0.2~0.3배 가량 낮았으며, 전체 노드에 간섭이 인가된 경우 0.5배 이상 뛰어난 성능을 보였다. 특히 ϵ(7.5) 이상의 수준에서는 2배 이상의 성능 차이를 보이며 AFBM과 비교하여 매우 높은 잡음 강인성을 확인할 수 있었다.
그림 7은 전체 입력 노드에 잡음의 간섭이 있을 경우, 간섭 정도에 따라 속도와 고도를 구간별로 나누어 예측 오차를 평균화한 것으로 X축을 기준으로 정렬하였다. 그림 7(a), 7(b)는 속도를 기준으로 나타낸 것으로서, 잡음의 간섭 수준과 관계없이 AFBM 대비 제안한 AFCP가 높은 예측 안정성을 보여주었다. 그림 7(c), 7(d)는 고도를 기준으로 나타낸 것으로서, 잡음의 간섭 수준이 증가할수록 일부 구간에서는 안정성이 기존 AFBM과 유사함을 보였지만, 이를 제외한 전 구간에 걸쳐 높은 예측 안정성을 갖는 것을 확인할 수 있었다.
종합적으로, 다양한 구조의 예측 알고리즘을 비교하여 제안된 MLP/LM의 성능을 입증하였을 뿐만 아니라 설계된 무작위 잡음을 삽입하여 예측 시스템이 갖춰야 할 잡음 강인성 비교 성능 평가를 수행하였다. 그 결과 제안된 예측 시스템은 간섭 노드와 관계없이 높은 예측력을 보여주었으며 잡음의 간섭이 증가할수록 기존 수학적 모델 대비 높은 강인성을 확인할 수 있었다.
Ⅴ. 결 론
항공기의 연료 시스템은 항공기 엔진의 안정적인 동작 여부를 결정짓는 항공기의 핵심적인 전자, 기계적 시스템 중 하나로서 안전한 비행을 위한 연료 시스템의 신뢰성은 무엇보다 중요하다. 하지만 현대의 항공기는 최첨단 기술과 장비의 탑재에도 불구하고 치명적인 결함뿐만 아닌 단순 결함 및 조종사 또는 정비사의 부주의로 인해 사고가 여전히 발생되고 있다. 이에, 본 논문에서는 높은 신뢰성이 보장되어야 하는 항공기 연료 시스템의 오류로 인한 사고 발생의 사전 방지를 위하여 항공기 연료 소모량 예측을 통한 항공기 연료 시스템 무결성 감시기법을 제안하였다.
제안된 시스템은 연료 시스템 내의 센서 게이지로부터 측정된 연료량과의 유사성을 비교하여 시스템의 이상 유무를 판단하며, 연료 시스템에서 발생가능한 결함을 사전에 인지 및 예방을 통해 전체적인 항공기 시스템의 신뢰성 향상을 목표로 하였다. 기존 수학적 모델이 내포하는 예측 부정확성의 가능성으로 인한 신뢰성 문제를 고려하여 신경망을 기반으로 설계하였으며 최적 설계를 위해 다양한 구조를 비교 평가하여 제안된 MLP/LM 구조의 적합성을 검증하였다. 실제 비행 환경에서 발생 가능한 잡음과 생략된 미세 변수에 대응하는 강인성 평가를 수행하였으며, 이를 통해 잡음의 간섭이 증가할수록 간섭 노드(속도, 고도)와 무관하게 AFBM 대비 평균 20~30%, 구간에 따라 최대 200% 이상 강인함을 보여주었다. 이로써, 제안된 AFCP는 실제 비행 환경에서의 항공기 연료 시스템 무결성 감시를 통한 항공기의 신뢰성 향상을 기대할 수 있을 것으로 사료되며, 향후 다양한 항공기 데이터를 응용한 추가 모의시험과 예측 시스템의 성능고도화를 위한 심화학습을 진행할 예정이다.
Acknowledgments
본 연구는 순천향대학교 학술연구비 지원으로 수행되었음
References
- G. D. Schilling, "Modeling Aircraft Fuel Consumption with a Neural Network", Virginia Polytechnic Institute and State University for the degree of master of science in civil engineering, Feb), (1997.
- Airbus, "Flying by numbers: Global Market Forecast for 2015-2034", Airbus, p40-46, Dec), (2015.
-
I. Pagoni, and V. Psaraki-Kalouptsidi, "Calculation of aircraft fuel consumption and CO2 emissions based on path profile estimation by clustering and registration", Transportation Research Part D: Transport and Environment, 54, p172-190, Jul), (2017.
[https://doi.org/10.1016/j.trd.2017.05.006]

- Boeing, "Statistical Summary of Commercial Jet Airplane Accidents 1959-2016", Boeing, Aug), (2017.
- World Aircraft Accident Summary reports 1990-2016, http://www.airsafe.com [Accessed: Jan. 30, 2018].
- Flight Profile and Distance by Carbon Offset Research and Education, http://www.co2offsetresearch.org [Accessed: Jan. 30, 2018].
- D. Kumar, A. Sharma, and S. K. Sharma, "Developing Model for Fuel Consumption Optimization in Aviation Industry", Innovative Systems Design and Engineering, 3(10), p26-37, Oct), (2012.
- M. Manngard, J. Kronqvist, and J. M. Boling, "Structural learning in artificial neural networks using sparse optimization", Neurocomputing, 272, p660-667, Jul), (2017.
- B. P. Collins, N. J. Bell, 이름 성, and D. W. Ford, "A Concept for Aviation Fuel Efficiency", Aviation Fuel Consumption Symposium, p10-11, Sep), (1984.
- A. C. Miranda, and V. M. Castaño, "Smart frost control in greenhouses by neural networks models", Computers and Electronics in Agriculture, 137, p102-114, May), (2017.
- W. Cao, X. Wang, Z. Ming, and J. Gao, "A review on neural networks with random weights", Neurocomputing, 275, p278-287, Sep), (2017.
-
X. F. Yuan, S. Ma, and S. H. Jiang, "Formfinding of tensegrity structures based on the Levenberg-Marquardt method", Computers and Structures, 192, p171-180, Nov), (2017.
[https://doi.org/10.1016/j.compstruc.2017.07.005]

- G. S. Kumar, and K. Rajasekhar, "Performance analysis of Levenberg-Marquardt and Steepest Descent algorithms based ANN to predict compressive strength of SIFCON using manufactured sand", Engineering Science and Technology, an International Journal, 20(4), p1396-1405, Aug), (2017.
- FAA, "Aircraft Data", Federal Aviation Administration Advisory Circular 150/5325-5C, Jun), (1987.
- I. Isaev, and S. Dolenko, "Training with Noise Addition in Neural Network Solution of Inverse Problems: Procedures for Selection of the Optimal Network", Procedia Computer Science, 123, p171-176, Jun), (2018.
- S. A. Bagherzadegh, "Nonlinear aircraft system identification using artificial neural networks enhanced by empirical mode decomposition", Aerospace Science and Technology, Jan), (2018.
-
H. Wang, Y. Wang, and Q. Hu, "Self-adaptive robust nonlinear regression for unknown noise via mixture of Gaussians", Neurocomputing, 235, p274-286, Apr), (2017.
[https://doi.org/10.1016/j.neucom.2017.01.024]


2018년 2월 : 한서대학교 항공전자공학과(공학사)
2018년 3월 ~ 현재 : 순천향대학교 전기통신시스템공학과 석사과정
관심분야 : 적응신호처리, 기계학습

2004년 12월 : Univ. of Florida 컴퓨터및전기공학과(공학박사)
2005년 ~ 2006년 : Univ. of Florida 의용공학과 박사후연구원
2006년 ~ 2007년 : 삼성전자 책임연구원
2007년 ~ 2014년 : 한국항공우주 연구원 선임연구원
2017년 3월 ~ 현재 : 순천향대학교 전기공학과 조교수
관심분야 : 시스템 FDE, GNSS 및 보강시스템, 기계학습