군집화 알고리즘을 이용한 채널 추정 기법 및 성능 평가

Ⅰ. 서 론

이동 통신 시스템에서 파일럿 신호 전송은 이동하는 단말과 기지국 사이의 채널을 추정하기 위하여 필수적이다. 파일럿 신호는 송신기와 수신기 사이에 사전에 알려져 있는 신호이므로 참조 신호(Reference Signal)이라고도 한다. 그러나 파일럿 신호는 제어신호로써 데이터를 전송하기 위한 무선 자원을 소비하므로 파일럿 신호의 전송은 실질적인 데이터 전송률을 감소시키는 원인이기도 하다. 따라서 일정 수준 이상의 무선 통신 시스템의 성능이 유지되는 한 파일럿 신호의 전송은 최소화시키는 것이 중요하다[1].

한편, 딥러닝(Deep Learning)은 다양한 분야에 적용되어 새로운 해결책을 제시해 주고 있다[2][3]. 기존 컴퓨터의 연산능력의 한계로 이론으로만 존재하였던 딥러닝 알고리즘은 현대의 막강한 계산 능력을 보유한 컴퓨터 하드웨어와 결합하여 실제로 구현되기 시작하였다. 최근 딥러닝 기법을 적용하여 QPSK(Quadrature Phase Shift Keying) 검파에 활용한 연구가 발표되었다[4]. 딥러닝이 적용된 연구들을 살펴보면, 기존에 제어 정보로 제공되던 정보들 없이 딥러닝 알고리즘을 사용하여 신호를 수신하는 목적의 연구가 주류를 이루고 있다[5].

본 논문에서는 딥러닝 자율학습 분야에서 사용되는 군집화 기법을 채널 추정에 적용하여 파일럿 신호 없이 데이터 QPSK 심볼만으로 채널을 추정할 수 있는 알고리즘을 제안하였다. 기존에 파일럿 신호를 사용하는 채널 추정 기법은 약속된 주파수 및 시간 자원에 송신기와 수신기에 미리 알려져 있는 신호를 전송하여 채널에 대한 계수를 검출하였다 [6]. 반면, 본 논문에서 제안하고 있는 파일럿을 사용하지 않는 채널 추정(PCE, Pilotless Channel Estimation) 기법은 데이터 심볼만을 군집화 알고리즘에 입력으로 제공하고 반복된 군집화 연산을 통하여 군집들의 중심점에 대한 신호 크기와 위상 변화를 검출하여 채널을 추정한다.

PCE 기법은 파일럿 신호를 위한 별도의 무선 자원을 소비하지 않기 때문에 파일럿 신호 전송에 사용된 만큼의 무선 자원에 대한 실질적인 전송률 개선 효과가 있다. 또한, 딥러닝에서 사용하는 군집화 기법의 특성상 평균화 연산과정에서 파생되는 잡음 감소 효과를 얻을 수 있어 기존의 파일럿 기반의 채널 추정 기법 대비 잡음에 강인한 특성을 갖게 된다.

PCE의 성능은 기존에 널리 사용되던 최소 자승(LS, Least square) 채널 추정기와 평균 자승 오차 및 비트 오류율 측면에서 비교하였다. 또한 PCE 알고리즘이 채널 추정 주기 측면에서 4세대 이동통신 및 5세대 이동통신에 실질적으로 적용될 수 있도록, LTE 시스템 및 5세대 이동통신 시스템의 동작 주파수 대역과 자원할당 단위를 고려한 적용 가능성 판단 결과를 제시하였다.

Ⅱ. 시스템 모델

OFDM으로 수신된 N개의 심볼을 고려한다. N개의 수신 심볼은 하나의 상관 시간(Coherence Time)과 상관 주파수 내에서 수신되며 다음과 같이 표현될 수 있다[7].

식 (1)에서 x_l는 M-ary 신호 중 l번째 심볼이 송신되었음을 의미하며, h는 단위 크기의 복소-가우시안(Complex-Gaussian) 확률 분포를 따른다. 잘 알려진 바와 같이 이와 같은 채널 모델을 레일리(Rayleigh) 채널이라고 한다. n은 백색잡음으로 역시 복소 가우시안 분포를 따르는 랜덤 변수이다[7].

N개의 수신 심볼은 K-means 알고리즘에 의해서 M개의 군집(Cluster)으로 구분된다[2]. L번 반복되어 검출된 군집의 중심점은 다음과 같이 계산될 수 있다.

식 (2)에서 S_m는 m번째 군집에 포함되는 심볼의 색인에 대한 집합이다. E[x]는 x에 대한 기대값을 계산하는 것으로 y_S(m)는 m번째 군집에 포함된 모든 심볼들에 대한 평균값이 된다. y_S(m)의 위상 값에 따라 오름차순으로 m값이 부여된다. 이렇게 결정된 중심점이 그림 1에 도시되어 있다.

그림 1에 있는 두 개의 성상도에서 위쪽의 성상도에는 임의로 결정된 중심점들이 도시되어 있고, 아래쪽에는 K-means 알고리즘을 사용하여 추정된 중심점들이 도시되어 있다. SNR은 0dB이었며, L=20회 알고리즘 반복 동작을 통해서 식 (2)를 기반으로 중심점을 구하였다. 이와 같은 군집화 기법은 백색잡음채널 환경에서 QPSK신호 검파에 활용된 바 있는데, 본 논문에서는 채널의 영향으로 중심점의 위치가 일반적인 QPSK의 성상점과 다름을 알 수 있다. 다중 경로 채널에 의해서 QPSK 심볼의 크기(Amplitude)와 위상(Phase)가 변화한 것으로 중심점에 채널의 영향이 반영되어 있다.

Fig. 1.

Center point estimation using K-means algorithm

Ⅲ. 파일럿 없는 채널 추정 기법

3.1 채널 추정 알고리즘

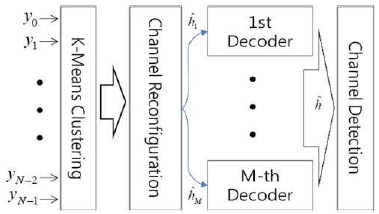
본 논문에서 제안하고 있는 채널 추정 기법이 그림 2에 도시되어 있다. N개의 심볼이 수신되면 K-means 알고리즘을 활용한 심볼 군집화를 통하여 식 (2)에 제시된 M개의 중심점을 추정한다. 이 때 M개의 중심점은 QPSK 참조심볼의 위치와 비교할 때 모호성을 가지게 된다. 참조심볼은 전형적인 QPSK 성상점에서 전송되는데, 예를 들면 제1사분면의 참조심볼 성상점이 그림 1의 아래 그림에서 어느 중심점에 대응되는지 알 수 없게 된다.

Fig. 2.

Channel estimation scheme using clustering algorithm

채널의 실수와 허수에 해당하는 계수를 추정하기 위하여 식 (1)의 채널을 다음과 같이 실수부와 허수부로 나누어 표현한다.

$\[ h=a+b_i \]$

(3)

식 (1)에서 전송되는 참조심볼 x_l, l=1,..., M 에 대하여 송신된 값은 다음과 같이 가정한다. 일반적으로 QPSK 심볼에 사용되는 값이다[7].

$\[ x_l=e^{j\frac{\left(2l-1\right)\pi }{4}},l=1,\dots ,M \]$

(4)

채널 추정을 하기 위하여 다음과 같이 두 개의 중심점에 대하여 식 (5)의 연산을 수행한다.

$\[ \overline{y_S}=\frac{y_S\left(1\right)+y_S\left(2\right)}{\sqrt{2}} \]$

(5)

앞에서 언급한 바와 같이 y_S(1)은 어떤 QPSK 심볼이 전송된 것인지 알 수 없다는 모호성이 존재한다. 따라서 y_S(1)이 x_l, l=1,2,3,4 네 개의 QPSK 심볼 중 하나가 전송된 것 가정할 때, 식 (5)는 다음과 같이 네 개의 값을 가질 수 있다.

$\[ \begin{array}{c}\overline{y_S}\left(1\right)=-b+j\cdot a+n_1,\hfill \\ \overline{y_S}\left(2\right)=-a-j\cdot b+n_2,\hfill \\ \begin{array}{c}\overline{y_S}\left(3\right)=b-j\cdot a+n_3,\hfill \\ \overline{y_S}\left(4\right)=a+j\cdot b+n_4.\hfill \end{array}\hfill \end{array} \]$

(6)

식 (6)에서 n_l, l=1,2,3,4 는 식 (4)와 (5) 계산 과정에서 평균화된 잡음이다. 식 (6)으로부터 추정된 채널 $$ \widehat{h}$$ 는 다음과 같이 계산된다.

$\[ \begin{array}{c}{\widehat{h}}_1=-j\cdot {\overline{y}}_S\left(1\right)=a+j\cdot b+n_1\hfill \\ {\widehat{h}}_2={\overline{y}}_S\left(2\right)=a+j\cdot b+n_2\hfill \\ \begin{array}{c}{\widehat{h}}_3=j\cdot {\overline{y}}_S\left(3\right)=a+j\cdot b+n_3\hfill \\ {\widehat{h}}_4={\overline{y}}_S\left(4\right)=a+j\cdot b+n_4\hfill \end{array}\hfill \end{array} \]$

(7)

n_l,l=1,2,3,4는 매우 작은 복소수 값이므로 계산과정에 따른 값의 변화를 따로 표시하지 않았다.

식 (7)에 의해서 추정 채널 값을 구하기는 하였으나 실제 채널은 식 (7)에 제시되어 있는 값들 중 하나이므로 그림 2에 도시되어 있는 바와 같이QPSK에 대해서 4회 복호화(Channel Decoding)를 수행한다. 채널 추정이 필수적인 이동통신 시스템의 경우 터보 코드와 같은 오류 정정 부호를 사용하고 있으며 오류 검출을 위하여 순환 중복 검사(CRC, Cyclic Redundancy Check)를 시행하므로 CRC 결과 오류가 없는 채널을 최종 추정 채널 $$ \widehat{h}$$으로 선택한다. $$ \widehat{h}$$에 대한 최초 채널 추정 이후 송신 심볼에 대한 모호성이 제거된다. 단말의 이동에 따른 시변 채널을 고려하더라도 채널의 위상이 급격하게 변화하지 않으므로, 송신 심볼에 대한 모호성 때문에 발생하는 복호화 복잡도 문제는 해결될 것으로 판단된다.

3.2 시변 채널에 대한 적용 가능성

본 논문에서 제안하고 있는 PCE 기법은 복수의 수신 심볼들에 대하여 K-means 군집화 알고리즘을 사용하므로, 수신 심볼의 수가 채널 추정 성능에 영향을 준다. K-means 군집화 알고리즘은 입력 샘플 수가 증가하면 군집화의 정확도가 개선되는 특징을 가지고 있다. 또한 PCE 기법은 최초 채널 추정 시 송신 심볼과 군집화된 중심점을 대응시키는 것에 대한 모호성을 극복하기 위하여 오류정정부호와 CRC를 활용하고 있으므로, 오류정정부호의 부호화를 위한 최소 자원할당 단위를 고려하여 설계되어야 한다[8].

가장 대표적인 이동통신 시스템인 3GPP LTE 시스템의 경우 15kHz 대역폭의 부반송파를 주로 사용하며 7 또는 14 OFDM 심볼 단위로 할당된 자원에오류정정부호화된 전송 블록(Transport Block)을 구성한다. 시간으로 환산하면 0.5 내지 1ms에 해당한다. 따라서 최초 채널 추정과 다음 채널 추정까지 두 개의 전송 블록이 필요하므로 최대 2ms 시간이 필요하다.

채널 추정 주기는 상관 시간에 의해서 결정된다. 상관 시간은 채널이 통계적으로 독립적인 값으로 변화하지 않는 평균적인 시간을 의미하며 상관 시간 내에 연속적인 채널 추정이 이루어져야 한다. 상관 시간 t_C는 신호가 전송되는 반송파 주파수 f_c, 단말의 속도 v에 의해서 결정되며 다음과 같은 식으로 표현될 수 있다. c는 전자기파의 전파 속도이다.

$\[ t_C=\frac{c}{v\cdot f_c} \]$

(8)

식 (8)에 의해서 계산된 상관 시간은 표 1에 정리되어 있다. 현재 LTE가 사용하는 2GHz 대역에서는 30m/s의 고속 이동 시에도 상관 시간이 5ms 이므로, 15kHz의 부반송파 간격(Subcarrier Spacing)을 사용하는 LTE 시스템에서 두 개의 부프레임(Subframe) 시간이 상관 시간 이내에 종료되어 연속적인 채널 추정이 가능하다. 그러나 5세대 이동통신에서 활용될 것으로 예상되는 6GHz 이상의 주파수 영역에서 음영으로 표시된 속도에서 채널 추정 주기는 상관 시간을 만족하지 못한다.

Table 1.

Coherence time considering velocity and carrier frequency

다양한 부반송파 간격을 사용할 수 있는 5세대 이동통신 시스템에서는 전송 블록으로 하나의 슬롯을 14 OFDM 심볼로 정의하고 있다[9]. 따라서 PCE는 슬롯 단위로 채널 추정 가능하다. 부반송파 간격이 증가함에 따라 슬롯의 시간은 반비례하기 때문에 6GHz 이상의 주파수 영역에서도 두 개의 슬롯 시간이 상관 시간보다 짧도록 할 수 있다. 반송파 주파수와 단말의 이동 속도를 고려하였을 때 표 1의 상관 시간을 만족하는 부반송파 간격을 표 2에 제시하였다. 예를 들어 설명하면 30GHz에서 20m/s의 이동 속도에서 PCE를 사용하기 위하여 60kHz 이상의 부반송파 간격을 사용하면 표 1에의 0.5ms 상관 시간을 만족시킬 수 있다.

Table 2.

Subcarrier spacing considering coherence time

Ⅳ. 채널 추정 성능 검증

본 논문에서 제안하고 있는 PCE 기법에 대한 성능을 검증하였다. 비교 대상은 파일럿 신호를 사용하는 최소 자승(LS, Least square) 채널 추정기이다. 일반적으로 채널 추정 시 채널 추정의 정확도는 평균 자승 오차(MSE), Mean Square Error)로 측정한다.

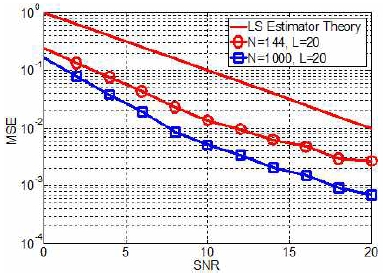
제안하는 PCE 기법에서는 파일럿을 사용하지 않았으며 QPSK 데이터 심볼만을 사용하여 채널을 추정하였다. 사용된 데이터 심볼 수 N은 144개와 1000개이다. 144개의 심볼은 12개의 부반송파와 제어신호용 OFDM 심볼을 제외하고 12개의 OFDM 심볼로 구성된 한 개의 자원 블록(Resource Block)이 전송되었을 때 전송할 수 있는 데이터 심볼 수이다. LTE 시스템에서 전송가능한 최소 단위 자원 할당 의 크기와 일치한다. 1000개의 심볼 수는 144개 보다 많은 수로, 실험을 통하여 그 이상의 심볼수를 사용하여도 성능개선이 크게 일어나지 않는 심볼 수이다.

그림 3에는 MSE 성능이 도시되어 있다. MSE 성능은 추정된 채널이 실제 채널과 유사한 정도를 의미한다. 사용한 심볼 수와 상관없이 제안한 채널 추정기의 MSE 성능이 LS 채널 추정기의 성능보다 우수하다. LS 채널 추청기의 경우 MSE 성능이 1/SNR로 결정되지만, 군집화 알고리즘을 사용하는 PCE 기법의 경우 중심점 추정 과정에서 잡음에 대한 평균화 연산을 통해서 정확한 채널 추정을 방해하는 잡음의 효과가 감소되기 때문이다.

Fig. 3.

MSE of estimation of clustering centers by K-means algorithm

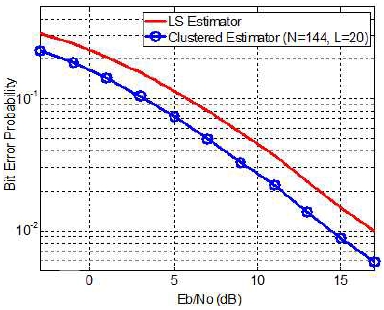
그림 4에 비트 오류율 성능이 도시되어 있다. PCE 기법에서 LS 채널 추정 기법 대비 MSE가 개선된 효과에 의해서 레일리 채널에서의 비트 오류율이 개선된 것을 확인할 수 있다. 비트당 잡음 비율을 기준으로 2dB 이상의 성능이 개선된 것을 확인할 수 있다.

Fig. 4.

MSE of estimation of clustering centers by K-means algorithm

V.결 론

본 논문에서는 딥 러닝 자율학습 분야에서 사용하고 있는 군집화 기법을 활용하여 파일럿 신호 없이 데이터 심볼 만으로 채널을 추정하는 PCE기법을 제안하였다. QPSK 심볼은 다중 경로 채널을 통과하면서 크기와 위상이 변화하게 되는데, PCE 기법은 군집화 기법을 무선 통신 수신 기법에 적용하여 송신된 심볼의 변화된 크기와 위상을 추정하였다. PCE의 성능은 널리 사용되는 최소 자승 채널 추정기와 비교하였고, 평균 자승 오차에서 신호대 잡음비 기준 7dB 이상의 성능 개선을 달성하였다. 또한 평균 자승 오차의 개선으로 파일럿을 사용하지 않았음에도 비트 오류율에 있어서도 2dB이상의 개선된 성능을 얻을 수 있었다.

Acknowledgments

본 연구는 2016학년도 상명대학교 교내연구비를 지원받아 수행하였음.

References

• O. Elijah, C. Y. Leow, T. A. Rahman, S. Nunoo, and S. Z. Iliya, "A Comprehensive Survey of Pilot Contamination in Massive MIMO-5G System", IEEE Commun. Surveys & Tutorials, Vol. 18(No. 2), p905-923, Feb.), (2016. [https://doi.org/10.1109/comst.2015.2504379]
• A. Coates, and A. Y. Ng, "Learning Feature Representations with K-Means", Lecture Notes in Computer Science, Vol. 7700, p561-580, (2012).
• S. Raschka, and V. Mirjalili, "Python Machine Learning: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow, 2nd Ed.", Packt Publishing, (2017).
• M. Xiao, and H. Wang, "Bit Error Rate Performance Evaluation of QPSK Signal Detected by Clustering in Deep Learning", Journal of Korean Institute Of Information Technology, Vol. 15(No. 12), p117-122, Dec.), (2017.
• H. Ye, G. Y. Li, and B. H Juang, "Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems", IEEE Wireless Commun. Letters, (Early Access), Vol. PP(No. 99), p1-5, Sep.), (2017.
• L. Fang, and L. Wu, "Deep learning detection method for signal demodulation in short range multipath channel", International Conference on Opto-Electronic Information Processing (ICOIP) 2017, p16-20, Jul.), (2017. [https://doi.org/10.1109/optip.2017.8030690]
• B. Sklar, "Digital Communications: Fundamentals and Applications 2nd Ed.", PrenticeHall, (2001).
• E. Dahlman, and S. Parkvall, "4G, LTE-Advanced Pro and The Road to 5G 3rd Ed.", Academix Press, (2016).
• 3rd Generation Partnership Project (3GPP), 3GPP TS 38.201(Physical Layer: General Description), Dec.), (2017.