지면효과를 갖는 쿼드로터에 대한 피드백 선형화기반 슬라이딩 모드 제어
초록
본 논문은 자율주행 쿼드로터의 지면효과에 대해 안정한 자세제어가 가능한 피드백 선형화기반 슬라이딩 모드 제어를 소개한다.제안된 방법은 적응제어 기법의 도입없이 지면효과 등의 외란에 대해 안정한 쿼드로터의 자세 유지 및 위치제어 성능을 갖는다. 쿼드로터의 출력변수를 x, y, z 위치와 yaw 각으로 두고, roll 및 pitch 제어 입력이 x, y, z 동역학에 명시적으로 포함되는 확장된 시스템에 대해 피드백 선형화 제어기를 설계하고, 폐루프 다이나믹스의 적분형을 슬라이딩 평면으로 설계하는 슬라이딩 모드 제어(FLSMC) 방법을 제안한다.전체 시스템의 점근적 안정도는 리아프노프 안정성 방법에 의해 확인된다. 시뮬레이션을 통해 초기에 30°의 롤, 피치 각에 대해 7초 이내에 안정한 자세 유지가 가능함을 보였으며,쿼드로터의 지면효과를 외란으로 고려한 결과, 제안된 방법의 자세제어에 대한 강인성을 보였다.
Abstract
This paper introduces feedback linearization based sliding mode control(FLSMC) for a ground effect of the autonomous quad-rotor. The proposed control without adaption scheme has the stable attitude and positioning capability of the quad-rotor in spite of ground effect. For output variables of quad-rotor, x-y-z position and yaw angle are selected. Dynamic extension of the quad-rotor dynamics is obtained so that roll and pitch control input are explicitly appeared in x-y-z dynamics, and then linearization control is designed. A sliding mode control with a class of feedback linearization is designed. Integral type of resulting closed loop dynamics is adopted for sliding surfaces design. The asymptotic stability of the overall system was assured based on Lyapunov stability methods. It was shown through simulation that attitude control is stable under initial condition of 30° roll, pitch angle and yaw. Robustness of the proposed method was shown for quad-rotor system with a ground effect as disturbance.
Keywords:
quad-rotor, sliding mode control, feedback linearization, UAV, ground effectⅠ. 서 론
무인비행기(UAV, Unmanned Aerial Vehicles)란 카메라, 센서, 통신장비 또는 다른 장비를 탑재하고 있으며 원격 조종되거나 스스로 조종되는 비행체를 말한다. UAV 시스템은 운용자가 직접 원격 조종하기도 하나, 사전에 경유지점과 최종 목표지점을 입력시켜 자율 비행을 하게하며, 지상국과 통신체계 그리고 비행체의 3가지 요소로도 이루어져 있는데, 대부분의 연구는 비행체의 자세제어에 대한 연구가 주를 이루고 있다[1].
특히, 쿼드로터(Quad-rotor)는 일반적으로 호버링 성능이 우수하고 기계적 구조가 간단하여 제작 및 유지보수 비용이 적으며, 로터의 운동에너지가 4개의 추력기로 분산되어 기동력 및 적재능력이 우수하여, 근래에 많은 분야에서 이러한 쿼드로터를 이용하려는 시도가 진행되어 왔다[2]. 특히, 택배 업무를 위한 용도나 고성능의 기능구현이 가능한 고가의 제품들이 출시되어지고 있는데 안전한 자세로 착륙하는 쿼드로터에 대하여 연구되어질 필요가 있다. 지표면 근처에서 비행중인 비행체에 대하여 지표면의 간섭으로 인해 발생되는 지면효과는 비행체의 착륙에 가장 큰 영향을 미치는 현상으로서 이에 대한 연구[3]가 오래전부터 이루어져 왔지만, 쿼드로터의 지면효과에 대한 연구는 미미한 실정이다.
쿼드로터 동역학은 공기역학에 영향을 받는 비선형이며, 강한 입력 불확실성에 노출되고, 적정한 추력 값을 분산시켜야 하는 조건을 만족해야 하며 모터 추력상수, 항력계수의 변동 등에도 강인한 자세제어 기술이 요구된다[4].
쿼드로터 제어방법으로 선형제어 및 수학적 모델링에 근거하지 않은 강화학습 방법이 있으나, 비선형 모델에 대하여 수학적 모델링을 기반으로 한 피드백 선형화(FL, Feedback Linearization) 방법의 적용에 대한 연구가 시도되었다[5]-[7]. FL 방법은 실제적 활동을 제한하는 상태 값에 대한 모든 정보를 요구하지만 측정된 상태 값들이 노이즈에 영향을 받는다. 이를 위해 사용되는 고성능의 센서는 시스템 전체의 비용을 비싸게 만든다. 또한 바람이나 지면효과 등의 외란에 민감한 성능을 보이는 문제점이 있다.
본 연구에서는 이와 같은 입력 불확실성을 갖는 쿼드로터의 견실한 제어를 위해 FL방법과 슬라이딩 모드 제어(SMC, Sliding Mode Control)를 합성한 방법을 제시한다. 주요 내용 및 구성은 다음과 같다.
2장에서는 적용된 쿼드로터 모델에 대해 간략히 기술하고, 3장에서 피드백 선형화에 기반한 SMC 설계방법을 제시한다. 4장은 시뮬레이션을 통해, 제시된 방법에 의해 적절한 추력 값을 유지하며 효과적인 자세유지가 가능함을 보이고, 마지막으로 5장에서 결론을 맺는다.
Ⅱ. 시스템 모델링
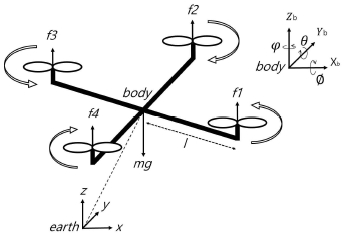
쿼드로터 시스템은 그림 1에 도시된 바와 같이 4개의 로터에 의해 구동되며, 각 로터의 회전 속도에 의해 자세 및 위치 제어를 수행한다. 본 연구에 사용된 로터는 x축과 y축에 대해 대칭이고, 무게중심과 기하중심과의 거리는 0이며, 무게중심으로부터 막대의 끝에 위치한 각 로터까지의 거리는 l이다. 각 로터는 x-y평면에 대하여 직각방향으로 추력 Fi(i=1, 2, 3, 4)을 발생시킨다. Ji는 각 축에 대한 관성 모멘트이며, m은 질량, ρ는 항력계수이다.
| (1) |
| (2) |
| (3) |
| (4) |
여기서 u1은 쿼드로터의 수직력 제어, u2, u3, u4는 각각 roll, pitch, yaw제어 입력이며, 그 운동방정식은 식 (5)~(11)과 같다[8].
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
여기서 sin(*),cos(*)는 s(*), c(*)로 표기하였다. 식 (11)에서 gr(z)은 지면효과로, 고도 z0 이하에서 작동되며, A는 지면효과 상수, zcg는 쿼드로터 무게중심의 고도이다.
Ⅲ. 제어기 설계
먼저 FL 방법을 적용하기 위해 쿼드로터의 출력을 x, y, z와 Ψ의 4개로 두고, 식 (5), (6), (7)의 우변에 제어입력 u2, u3가 명시적으로 나타날 때까지 연속 미분을 취하는 동적 확장(Dynamic Extension)을 수행한다.
단순한 서보 모델의 정립을 위해 φ, θ, Ψ≪1로 두고, 지면효과를 배제하면 식 (5)~(10)은 식 (12)~(17)로 정리된다[7].
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
동적 확장의 결과, 부록A의 식 (A7)로부터 FL에 기반한 제어는 식 (18)과 같다.
| (18) |
여기서,
| (19) |
| (20) |
| (21) |
여기서 ex=x-xd, ey=y-yd, ez=z-zd, xd, yd, zd는 각각 해당 기준입력이고, kij>0, (i=1,2,3, j=1,2,3,4)이며, Us=[us1 us2 us3]T는 설계하고자하는 SMC입력이다. 그리고 [e1, e2, e3]≡[ex, ey, ez]로 두고, 식 (18)을 식 (12)~(16)에 적용하면 식 (22)와 같다.
| (22) |
각 슬라이딩 면을 식 (23)과 같이 설정하고, 식 (24)와 같이 usi를 설계한다[8].
| (23) |
| (24) |
여기서 ηi>0, ωi>0이며, 식 (22), (23), (24)로부터 리아프노프 안정성을 위한 조건 식 (25)가 충족됨을 확인할 수 있다.
| (25) |
그리고 Ψ제어기는 (26)을 적용한다.
| (26) |
Ⅳ. 시뮬레이션
본 논문에서 제안된 FL 기반의 SMC의 성능 확인을 위해 사용된 공칭 쿼드로터의 무게중심으로부터 로터까지의 거리는 l=1m, g=9.81m/s2, 그리고 식 (11)의 지면효과 관련 파라미터는 z0=2m, zcg=0.5m, A=0.4668로 두고[8], FL 제어결과와 비교하며 시뮬레이션을 진행하였다.
초기 위치는 x0=10m, y0=10m, z0=20m, 초기 오일러 각은 φ0=30°, θ0=30°, Ψ0=30°, 그리고 경유점은 xw=20m, yw=-10m, zw=10m, 목표점은 xf=0m, yf=0m, zf=0m로 두고, 25초 동안 시뮬레이션 하였으며, 선정된 제어 파라미터 값은 다음과 같다.
| (27) |
| (28) |
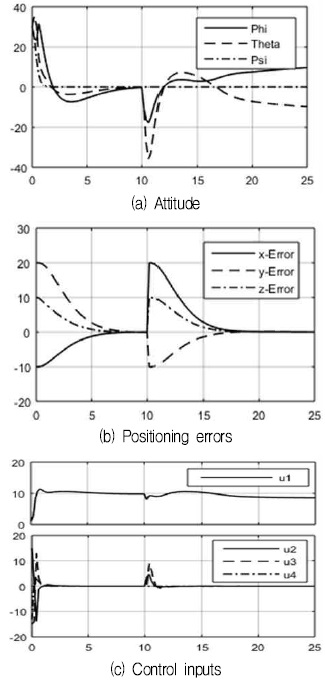
먼저 FLC에 따른 자세, 위치제어 시뮬레이션 결과는 그림 2(a)와 같이 약 7초 이내에 모든 자세가 안정화되며, 그에 따라 그림 2(b)와 같이 모든 위치제어 성능을 보였다. 하지만 고도가 2m 이하로 낮아지게 될 때, 지면효과로 인해 roll, pitch 각이 약 10°의 기울기를 나타내며 늦은 응답을 나타내었다. 그리고 그림 2(c)에 과도하지 않은 초기 제어입력을 보였다.
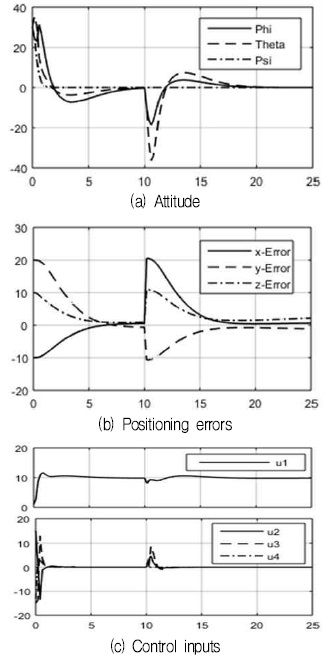
제시된 FLSMC 결과, 지면효과로 인해 그림 3(b)와 같이 위치 응답이 느리게 나타났지만, 그림 3(a)와 같이 급속한 자세 안정화가 이루어지는 것을 보였다. 고도가 2m 이하로 하강할 때, 지면효과의 영향을 감쇠시키며 roll, pitch, yaw 모두 안정하게 제어되는 것을 확인할 수 있으며, 특히, 지면효과에 대한 FLSMC 방법의 강인한 자세 안정성을 보였다.
그림 4는 지면효과와 같은 다른 외란에 대해서도 강인성을 보이는 FLSMC의 제어결과이다. 외란은 각각 x, y에 대하여 진폭 1m를 가지는 사각파형과 사인파형을 인가하였으며, z에는 평균과 표준편차가 0m, 1m를 가지는 랜덤 노이즈로 인가하였다.
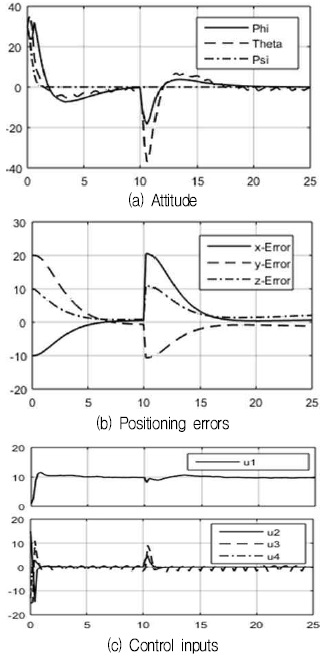
Attitude response, positioning error and control inputs in case of FL based SMC with ground effect and additional disturbance
목표위치로 도달하는 과정에서 그림 4(b)와 같이 느린 x, y, z 위치응답을 나타내나, 그림 4(a)에서 roll, pitch, yaw 각 모두 급속한 자세 안정화가 이루어지는 것을 확인하였다.
Ⅴ. 결론 및 향후 과제
본 논문에서는 지면효과를 갖는 쿼드로터에 대한 FL 방법에 기반한 슬라이딩 모드 제어(FLSMC)를 제시하였다. 출력변수를 x, y, z 위치와 yaw각으로 두고, roll, pitch 제어입력이 x, y, z 동역학에 명시적으로 포함되는 동적 시스템으로 변환하여 피드백 선형화 제어기를 설계하였다.
그리고 폐루프 다이나믹스의 적분형으로 설계한 슬라이딩 평면에 기초하여 리아프노프 안정성 조건이 충족됨을 보였다.
특히, 고도 2m 이하에서의 지면효과에 대해 기존의 FLC와 제시된 방법에 의한 자세제어를 비교한 시뮬레이션 결과, 기존의 방법은 roll, pitch 각 모두느린 응답을 나타내며, 약 10°의 기울기를 보이는 반면, 제시된 방법은 보다 급속하게 모든 자세의 안정화 성능을 보였다. 향후에는 위치 값에 인가되는 외란이 자세제어 에 미치는 영향에 대하여 분석하고, 지면효과 상태변수의 추정 및 적응제어기법의 적용에 대한 연구가 계속될 예정이다.
Acknowledgments
이 논문은 2016학년도 동의대학교 연구년 지원에 의해 연구되었음
References
- http://www.kosen21.org, , [Accessed : Jan. 04, 2018]
-
Y. M. Kim, and W. B. Baek, "Terminal Sliding Mode Hovering Control for Quadrotor with Input Uncertainty", Journal of KIIT, Vol. 14(No. 2), p7-12, Feb., 29), (2016.
[https://doi.org/10.14801/jkiit.2016.14.2.7]

-
A. Benallegue, A. Mokhtari, and L. Fridman, "Feedback Linearization and High Order Sliding Mode Observer For A Quadrotor UAV", Proc of the 2006 International Workshop on Variable Structure Systems, p365-372, Jun., 5-7), (2006.
[https://doi.org/10.1109/vss.2006.1644545]

-
H. Voos, "Nonlinear Control of a Quad-rotor Micro-UAV using Feedback Linearization", IEEE Int. Conf. on Mechatronics, p1-6, Apr.), (2009.
[https://doi.org/10.1109/icmech.2009.4957154]

-
D. H. S. Maithripala, and J. M. Berg, "Robust Tracking Control for Under-actuated Autonomous Vehicles using Feedback Linearization", IEEE/ ASME Int. Conf. on Advanced Intelligent Mechatronics, France, p446-451, Jul.), (2014.
[https://doi.org/10.1109/aim.2014.6878118]

-
S. A. Al-Hiddabi, "Quadrotor control using feedback linearization with dynamic extension", ISMA, Int. Symposium on ISMA, p1-3, Mar.), (2009.
[https://doi.org/10.1109/isma.2009.5164788]

-
D. W. Lee, H. J. Kim, and S. Sastry, "Feedback Linearization vs. Adaptive Sliding Mode Control for a Quadrotor Helicopter", Journal of Contorl, Automation, and Systems, Vol. 7(No. 3), p419-428, Jun.), (2009.
[https://doi.org/10.1007/s12555-009-0311-8]

- N. Mezghani, B. Romdhane, and T. Damak, "Terminal sliding mode feedback linearization control", IJ-STA, Vol. 4(No. 1), p1174-1187, Jul.), (2010.
Appendix
저자소개

2009년 2월 : 동의대학교 메카트로닉스공학과(공학사)
2011년 2월 : 동의대학교 지능시스템공학과(공학석사)
2015년 3월 ~ 현재 : 동의대학교 지능시스템공학과(공학박사수료)
관심분야 : Nonlinear System, Quad-rotor UAV, Sliding Mode Control

1993년 2월 : 부산대학교 기계공학과(공학박사)
1993년 ~ 2001년 : 삼성중공업 선임연구원
2002년 ~ 현재 : 동의대학교 로봇자동화공학과 교수
관심분야 : HOSM, 자동차 지능제어, 비선형 제어, 로봇 시스템, 로봇 지능