동적 방향 대수적 영상복원법에서 주사순서와 수렴성능에 관한 연구
초록
전기 커패시턴스 단층촬영법(ECT, Electrical Capacitance Tomography)에서 동적 영상복원법은 빠르게 변하는 도메인 내의 유전율 분포를 알아내기 위해 제안되었다. 그러나 기존의 동적 복원방법은 복원을 위해 사용되는 자코비안(Jacobian) 행렬의 계산시간이 데이터 측정시간보다 더 걸리는 등의 문제로 실시간 모니터링에 적용하기에는 어려움이 있다. 최근 제안된 동적 방향 대수적 영상복원법(DART, Directional Algebraic Reconstruction Technique)은 자코비안 행렬의 계산이 불필요하고 단순히 행렬의 곱셈만으로 내부 유전율 분포를 복원할 수 있다. 이 논문에서 우리는 동적 DART의 복원성능 향상을 위해, 주사방향과 수렴성능과의 관계에 대하여 컴퓨터 모의실험을 통하여 연구하였으며, 기존의 순차주사방법보다 비월주사방법이 우수한 수렴성능을 가짐을 보였다.
Abstract
In electrical capacitance tomography (ECT), dynamic image reconstruction has been proposed to find the permittivity distribution within a rapidly changing domain of interest. However, the proposed dynamic reconstruction methods are difficult to apply to real-time monitoring because of the problem that the calculation time of the Jacobian matrix used for restoration is longer than the data measurement time. Recently, the proposed dynamic directional algebraic reconstruction technique (DART) does not require the calculation of the Jacobian matrix and can simply restore the internal permittivity distribution by simply multiplying the matrix. In this paper, we investigates the relationship between the scanning direction and the convergence performance by computer simulation to improve the dynamic performance of dynamic DART, and show that the interlaced scanning method has better convergence performance than the conventional progressive scanning method.
Keywords:
electrical capacitance tomography, dynamic directional algebraic reconstruction technique, scanning orderⅠ. 서 론
전기 커패시턴스 단층촬영(ECT, Electrical Capacitance Tomography)은 대상의 외부에 있는 전극들 사이에서 획득된 커패시턴스로부터 대상의 내부 유전율 분포를 알아내는 것이다. ECT는 비교적 저렴한 하드웨어의 사용과 빠른 응답 및 휴대성의 장점이 있지만 복원영상의 낮은 공간해상도 때문에 장치산업(Process Industry)영역에 주로 응용되어 왔다[1]-[4].
ECT를 위한 영상복원기법에는 선형 역투사법(LBP, Linear Back-Projection), 티코노프 조정방법(Tikhonov Regularization Method), Landweber 반복법 및 방향 대수적 영상복원기법(DART, Directional Algebraic Reconstruction Technique) 등이 있으며 이 방법들은 모든 커패시턴스를 획득하는 동안 내부 유전율 분포는 변하지 않는다(정적(Static)인 상태)고 가정하였다[2]-[6]. 그러나 데이터를 측정하는 동안 유전율 분포가 변하게 되면(동적(Dynamic)인 상태) 이 방법들로부터 만족스러운 결과를 얻기 힘들다.
이와 같이 내부 상태가 시간에 따라 변하는 경우를 위해, 동적 영복복원법이 개발되었다[7]. 이 방법은 칼만(Kalman) 필터를 사용하여 상태가 시간에 따라 변하는 비선형 상태 추정문제로 다룬다. 동적 알고리즘은 각 전극의 여기마다 유전율 분포를 추정하는 것이 가능하여 한 프레임의 커패시턴스로부터 전극의 개수만큼의 복원영상을 얻을 수 있다. 그러나 이 방법은 자코비안(Jacobian) 행렬 등을 포함하는 알고리즘의 계산시간이 데이터 취득시간보다 길어질 수 있기 때문에 실제 적용에서 온라인으로 사용할 수 없다. 최근 제안된 동적 DART 알고리즘은 영상복원 성능이 우수한 정적 DART를 기반으로, 하나의 여기전극에 의해 측정된 커패시턴스로부터 복원영상을 얻도록 수정하였다[8]. 더욱이 DART 알고리즘은 자코비안 행렬 등의 복잡한 계산이 불필요하여 온라인으로 사용할 수 있다.
이 논문에서는 동적 DART 알고리즘의 영상복원 성능의 향상을 위하여 여기전극의 순서(주사순서)와 복원영상의 수렴성능에 관하여 연구하고 최적의 여기전극의 순서를 찾는다. 연구를 위하여 컴퓨터 모의실험을 활용하였으며, 비월주사법이 기존의 순차주사법보다 우수한 수렴성능을 가짐을 확인하였다.
Ⅱ. 데이터 획득과 전기장중심선
2.1 기존의 데이터 획득방법(정적 복원)
ECT에서 측정 데이터인 커패시턴스는 다중 송신장치(Multiplexing Unit)와 다수의 커패시턴스 검출기로부터 획득된다. 16-전극 센서에 대하여, 1-15번 전극은 하나씩 소스전극으로 사용된다. 1번 전극을 여기시켰다면, 2-16번 전극은 검출전극이 되며, 1번 전극과 다른 검출전극 사이의 커패시턴스를 각각 측정한다. 다음으로, 2번 전극을 여기시킨 상태에서 3-16번 전극 사이의 커패시턴스를 각각 측정한다. 같은 방법으로 3-15번 전극도 순서대로 여기시키면서 커패시턴스를 측정한다. 일반적으로 L-전극 센서에 대하여 L(L-1)/2개의 독립된 커패시턴스가 얻어지고, 16-전극 센서에 대하여 총 120개의 독립된 커패시턴스가 얻어진다[4][9]. 이렇게 얻어진 커패시턴스는 내부 유전율 분포를 얻기 위한 복원 알고리즘의 입력으로 사용된다.
2.2 전기장중심선의 그룹화
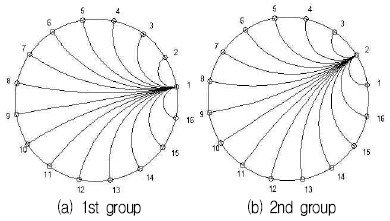
동적 DART에서 각 전극사이의 경로로써, 각 전극사이의 전기장중심선(EFCL, Electrical Field Centre Line)을 사용하였다. EFCL은 센서가 원형이고 내부가 동질일 때 나타나는 전기장 선의 중심선을 원의 일부로 근사화한 것이다[8]. 그림 1은 동질인 유전율 분포에서 1번째 및 2번째 그룹의 EFCL들로 도메인 내부의 선들은 EFCL들이고 경계부분의 작은 원은 각 전극의 중심이다.
그림 1에서 EFCL은 각 전극 쌍의 중심 사이를 원의 일부로 연결한 것이다. L-전극 센서에서 그룹의 수는 전극의 수와 같은 L개이고 한 그룹의 EFCL 수는 (L-1)개이며 전체 EFCL의 수는 독립된 측정의 수와 같은 L(L-1)/2개다.
2.3 수정된 데이터 획득방법(동적 복원)
기존의 커패시턴스 획득방법(2.1절)으로 얻은 커패시턴스를 동적 복원방법의 입력 데이터로 그대로 사용할 수 없다. 왜냐하면 측정된 커패시턴스에 대응되는 독립된 EFCL의 수는 L(L-1)/2개로 같지만, 각 그룹의 EFCL의 수는 (L-1)개씩이고 총 그룹의 수는 L이므로 L개 방향의 복원에서 사용되는 전체 커패시턴스의 수는 L×(L-1)이 되고, 각 커패시턴스는 두 번씩 사용되기 때문이다. 그러므로 동적 복원을 위한 커패시턴스 측정은, L-전극 시스템에서 1에서 L번 전극 모두가 여기전극이어야 하고, 여기전극이 바뀔 때마다 여기전극과 다른 전극 사이에서 측정된 (L-1)개의 커패시턴스를 데이터로 사용할 수 있도록 측정 방식을 바꾸어야 한다. 결국 수정된 데이터 획득방법으로 측정된 모든 커패시턴스의 수는 L×(L-1)개가 된다.
Ⅲ. 동적 방향 대수적영상복원법
그룹화 된 EFCL과 이에 대응하는 커패시턴스로부터 보간법(Interpolation)을 이용하면 EFCL과 관심영역 내부의 메시(Mesh)들 사이의 관계를 나타내는 수정된 가중행렬을 유도할 수 있다[8]. 동적인 유전율 분포에서 측정된 커패시턴스로부터 복원영상을 얻기 위한 동적 DART 알고리즘은 다음과 같다.
| (1) |
여기서 i=1,2,⋯, L, ϵi∈RM×1은 유전율 벡터, M은 메시의 수, Wi는 i번째 그룹에 대한 가중행렬, Ci∈R(L-1)×1은 i번째 전극을 여기하였을 때 측정된 커패시턴스 벡터이고 T는 전치(Transpose)이다.
Ⅳ. 주사순서 :전극의 여기 순서
TV 시스템에서, 순차주사(PS, Progressive Scanning)은 화면의 왼쪽 위에서부터 1줄씩 순서대로 화면의 오른쪽 아래까지 표시하여 한 프레임의 영상을 표시하는 것으로 선명한 영상을 표시하는 장점이 있지만, 움직임이 심한 영상에서는 잔상이 남는 등의 문제점이 있다. 이런 단점을 극복하기 위해 고안된 것이 비월주사(Interlaced Scanning, IS)이다. 비월주사는 한 프레임의 영상을 주사하는데 한 줄 건너 두 번의 주사로 전체의 면을 주사하는 방식으로 1회째는 홀수 번째 선을 주사하고, 두 번째는 짝수 번째 선을 주사하여 완전한 하나의 화면을 만든다. 1초에 30번 화면을 그리는 순차주사에 비해, 비월주사는 해상도가 떨어지지만 1초에 60번 화면을 그리기 때문에 깜빡거림이 적고 움직임이 심한 장면에서 잔상을 없애는 등의 장점이 있다.
동적 DART 알고리즘에서도 L개의 여기전극의 순서를 1번 전극에서부터 순차적으로 여기하는 것(순차주사)과 전극을 몇 개 뛰어 넘어서 여기하는 것이 복원 성능에 미치는 영향에 대해서 연구가 필요하다. 더욱이 수평적으로 주사하는 TV 시스템과는 달리 여러 방향으로 주사하는 원형인 ECT 센서에서 주사순서(여기전극의 순서)는 복원 성능에 많은 영향을 줄 것으로 예상할 수 있다.
복원 성능을 비교하기 위한 주사순서는 표 1과 같다. 여기서 PS와 IS는 각각 순차와 비월주사이다.
Ⅴ. 모의실험
성능을 확인하기 위하여 표 1의 주사순서에 대한 컴퓨터 모의실험을 수행하였으며, 영상복원을 위하여 그림 2(a)와 같이 1948개의 삼각형 메시를 가지는 ECT 센서를 사용하였다. 이 센서는 지름이 8cm이고 16개의 전극을 가진다. 배경(공기)과 표적(물)의 유전율은 각각 1과 80으로 가정하였고 초기값 벡터 ϵ0는 영(Zero) 벡터를 사용하였다.
그림 2(b)는 모의실험에 사용할 원래 영상으로 도메인의 가운데에 표적이 하나만 있는 정적 영상이다. 원래 영상이 그림 2(b)의 하나인 이유는 가장 자리에 표적이 있는 경우에 표적의 위치에 따라 동일한 주사순서임에도 수렴성능이 다르게 나오기 때문에 오직 주사순서에만 수렴성능이 결정되는 그림 2(b)의 경우로 한정하였다. 모의실험은 그림 2(b)의 원래 영상에서 측정된 커패시턴스에 대하여 표 2에 나오는 주사순서로 영상을 복원하였다. 특히, 수렴성능을 알아보기 위하여 각 주사방법마다 전극을 160번 여기(10 프레임)하여 160개의 영상을 복원하였다. 그리고 복원성능에 대하여는 정성적인 방법과 정량적인 방법의 두 가지로 비교하였다.
그림 3은 7가지 주사순서에 대한 복원영상으로 각 줄은 순서대로 4번째, 8번째, 16번째 및 160번째 전극여기에 의해 얻어진 커패시턴스로부터 복원된 영상이다. 첫 번째 행의 영상들을 보면 1번 전극(3시 방향)으로부터 반시계 방향으로 변하는 주사순서를 확인할 수 있고 네 번째 행의 영상을 통해 모든 주사방법에서 표적을 잘 찾는 것을 알 수 있다.
그림 3의 두 번째 행의 8번째 얻어진 영상으로부터 모든 주사방법에서 가운데 표적이 있는 것을 알 수 있다. 이것은 16개의 여기전극에서 얻은 데이터(1 프레임 데이터)를 사용하는 정적 복원방법보다 적은 수의 데이터로부터 도메인 내부 상태를 추측할 수 있는 동적 복원방법의 장점이다. 특히, 비월 주사방법의 결과에서는 대부분 4번째 얻어진 영상에서 가운데 표적이 있는 것을 확인 할 수 있고 따라서 비월주사방법이 순차주사방법보다 표적을 더 빠르게 찾을 수 있다.
다음으로 정량적인 비교를 위하여 영상오차(IE)와 상관계수(CC)를 다음과 같이 각각 정의하였다.
| (2) |
| (3) |
여기서 은 복원된 영상의 유전율 분포이고, g는 원래 영상의 유전율 분포이고, 과 는 각각 g과 의 평균값이다. 영상오차는 작을수록, 상관계수는 1에 가까울수록 더 좋은 성능을 나타낸다.
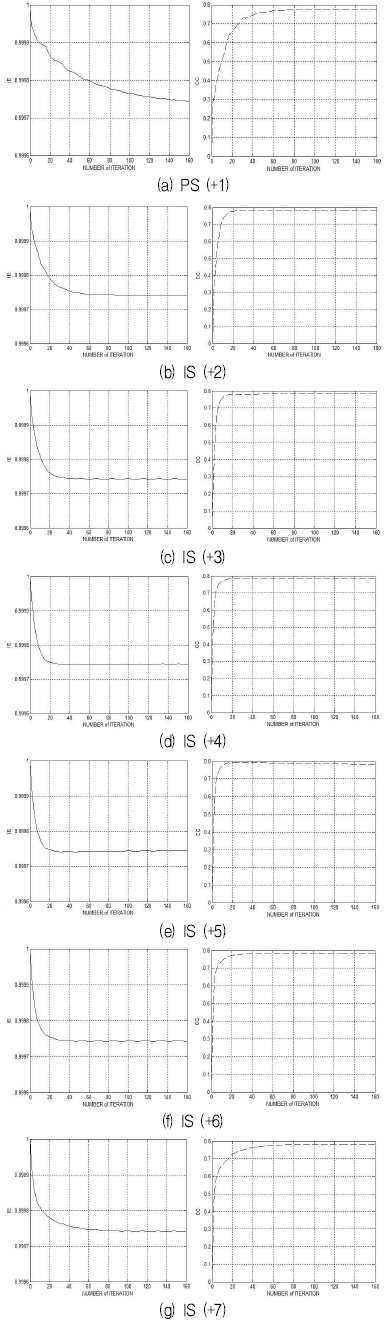
그림 4는 7가지 주사순서에 대한 영상오차와 상관계수를 각각 나타낸 것이다. 결과로부터 비월주사방법이 순차주사방법보다 더 빠르게 수렴한다는 것을 알 수 있다. 동적 영상복원에서는 초기 수렴성이 중요하므로 비월주사방법이 더 유용하다고 할 수 있다.
표 2는 그림 4의 영상오차와 상관계수에서 가장 좋은 값을 정리한 것이다. 차이는 기존의 방법인 순차주사와의 차이이다.
표 2에서 비월주사방법이 순차주사방법보다 영상오차와 상관계수 관점에서 더 좋은 수렴성능을 보임을 알 수 있으며, 비월주사방법 중에서도 ‘비월 (+5)’가 가장 좋은 수렴성능을 가짐을 알 수 있다.
Ⅵ.결 론
지금까지 ECT에서는 정적 복원방법들이 주로 연구되어왔다. 그러나 데이터를 얻는 동안에 내부 유전율이 변하면 이들 방법으로는 만족할만한 복원영상을 얻을 수 없었다. 이를 극복하기 위해, 유전율 분포가 동적인 경우에도 추정하기 위한 방법인 동적 복원방법들이 제안되었다. 이 논문에서는 온라인에 적용 가능한 동적 DART 알고리즘의 수렴성능 향상을 위해, 주사방향과 복원 성능에 대하여 연구하였다. 컴퓨터 모의실험을 통하여 다음과 같은 몇 가지 사실을 확인하였다.
첫째로, 동적 복원방법은 정적 복원방법에 비하여 더 적은 수의 측정 데이터로부터 내부 유전율 분포를 알 수 있다. 다음으로, 동적 복원방법에서 제안하는 비월주사방법이 기존의 순차주사방법에 비하여 더 빠른 수렴성능을 가지게 되어 더 적은 수의 데이터로부터 내부 유전율 분포를 알 수 있었다. 마지막으로, 16전극 ECT 센서의 경우, 제안하는 비월주사방법들 중에서 ‘비월 (+5)’방법이 가장 우수한 복원 성능을 가진다.
References
-
Ø. Isaksen, A. S. Dico, and E. A. Hammer, "A capacitance-based tomography system for interface measurement in separation vessels", Meas. Sci. Technol, Vol. 5(No. 10), p1262-1271, Oct.), (1994.
[https://doi.org/10.1088/0957-0233/5/10/011]

-
Ø. Isaksen, "A review of reconstruction techniques for capacitance tomography", Meas. Sci. Technol, Vol. 7(No. 3), p325-337, Mar.), (1996.
[https://doi.org/10.1088/0957-0233/7/3/013]

-
W. Q. Yang, and L. Peng, "Image reconstruction algorithms for electrical capacitance tomography", Meas. Sci. Technol, Vol. 14(No. 1), pR1-13, Jan.), (2003.
[https://doi.org/10.1088/0957-0233/14/1/201]

-
C. G. Xie, S. M. Huang, B. S. Hoyle, R. Thorn, C. Lenn, D. Snowden, and M. S. Beck, "Electrical capacitance tomography for flow imaging: system model for development of image reconstruction algorithms and design of primary sensors", IEE Proc.-G, Vol. 139(No. 1), p89-98, Feb.), (1992.
[https://doi.org/10.1049/ip-g-2.1992.0015]

-
W. Q. Yang, D. M. Spink, T. A. York, and H. McCann, "An image reconstruction algorithm based on Landweber's iteration method for electrical capacitance tomography", Meas. Sci. Technol, Vol. 10(No. 11), p1065-1069, Nov.), (1999.
[https://doi.org/10.1088/0957-0233/10/11/315]

-
J. H. Kim, B. Y. Choi, and K. Y. Kim, "Novel iterative image reconstruction algorithm for electrical capacitance tomography: directional algebraic reconstruction technique", IEICE Trans. Fund, Vol. E89-A(No. 6), p1578-1584, Jun.), (2006.
[https://doi.org/10.1093/ietfec/e89-a.6.1578]

-
M. Soleimani, M. Vauhkonen, W. Yang, A. Peyton, B. S. Kim, and X. Ma, "Dynamic imaging in electrical capacitance tomography and electromagnetic induction tomography using a Kalman filter", Meas. Sci. Technol, Vol. 18(No. 11), p3287-3294, Sep.), (2007.
[https://doi.org/10.1088/0957-0233/18/11/004]

-
J. H. Kim, B. S. Kim, K. Y. Kim, and I. S. Lee, "Dynamic Directional Algebraic Reconstruction Technique for Electrical Capacitance Tomography", JKIIT, Vol. 15(No. 11), p117-123, Nov.), (2017.
[https://doi.org/10.14801/jkiit.2017.15.11.117]

-
W. Yang, "Design of electrical capacitance tomography sensors", Meas. Sci. Technol, Vol. 21(No. 4), p1-13, Apr.), (2010.
[https://doi.org/10.1088/0957-0233/21/4/042001]


2000년 2월 : 금오공과대학교 전자제어공학과(공학사)
2002년 2월 : 경북대학교 전자공학과(공학석사)
2007년 2월 : 경북대학교 전자공학과(공학박사)
2007년 3월 ~ 현재 : 경북대학교 전자공학부 외래교수 및 초빙교수
관심분야 : inverse problem, electrical tomography, 추정이론

1994년 8월 : 한국과학기술원 전기및전자공학과(공학박사)
1986년 10월 ~ 1996년 2월 : 한국 전자통신연구원 선임연구원
1999년 8월 ~ 2000년 7월 : 미국 Stanford University 객원교수
1996년 3월 ~ 현재 : 우석대학교 정보기술학과 교수
관심분야 : IT융복합기술, 스마트그리드, 신재생에너지

1986년 : 경북대학교 전자공학과(공학사)
1989년 : 동대학원 졸업(공학석사)
1997년 : 동대학원 졸업(공학박사)
2005년 8월 ~ 2007년 1월 : 샌디에고 주립대학교 Research scholar
1997년 ~ 2008년 2월 : 상주대학교 전자전기공학부 교수
2008년 3월 ~ 2014년 10월 : 경북대학교 산업전자공학과 교수
2014년 11월 ~ 현재 : 경북대학교 IT대학 전자공학부 교수
관심분야 : 시스템 고장진단 및 고장허용제어, 지능제어 및 응용, 지능형센서시스템, electrical tomography