Rate Monotonic 스케줄링 알고리즘의 성능 향상을 위한 다중 계층 경쟁 회피 스케줄링 기법


초록
실시간 시스템에서의 작업들을 스케줄링하기 위한 알고리즘은 시스템 전체의 성능에 막대한 영향을 미치므로 매우 중요한 요소이다. 최신 스케줄링 기법인 다중 계층 경쟁 회피 스케줄링 기법(Multi-level Contention-free Policy)은 기존 스케줄링 알고리즘들에 적용 하여 성능을 비약적으로 향상 시키는 기법임에도 불구하고 EDF (Earliest Deadline First) 스케줄링 알고리즘에만 적용되어 있다. 본 연구에서는 다중 계층 경쟁 회피 스케줄링 기법을 RM에 적용하고 이를 위한 실시간성 분석 기법을 제안한다. 자체 개발한 시뮬레이터를 이용한 실험결과를 통해 프로세서의 개수와 다중 계층 회피 기법의 계층 높이에 따라, EDF에 비해 최대 53.2%의 성능 향상이 있음을 확인하였다.
Abstract
A real-time scheduling algorithm for a real-time system is a very important factor because it greatly affects the performance of the entire system. Although the multi-level contention-free policy is the novel technique to significantly improve the performance of existing scheduling algorithms, it has been only applied to EDF (Earliest Deadline First) scheduling algorithm. In this study, we apply the multi-level contention-free policy to RM (Rate Monotonic), and propose a real-time analysis technique for it. Via simulations, we identified up to 53.2% the performance improvement compared to EDF when various numbers of processors and layer heights of multi-level contention-free policy are considered.
Keywords:
real-time system, deadline, rate monotonic scheduling, multi-level contention-free policyⅠ. 서 론
실시간 시스템은 안전성이 최우선시 되는 내장형 시스템으로서 수행 되어야 하는 작업이 반드시 정해진 마감시간 내에 끝마치도록 요구되는 시스템이다[1][2]. 예를 들면, 운전자가 브레이크를 밟으면, 자동차의 내장형 기기는 아주 짧은 시간 내에 자동차의 제동 장치에 명령을 내려 속도를 줄일 수 있어야 한다. 만약 주어진 시간 내에 제동하지 못하면 치명적인 결과를 초래할 수 있다. 이와 같이, 마감 시간으로 표현되는 시간적 요구사항을 가지는 작업을 실시간 작업라고 한다. 실시간 작업들의 우선순위를 정하는 실시간 스케줄링 알고리즘과 정해진 마감 시간 내에 모두 처리할 수 있는지를 분석하는 실시간성 보장 분석 문제는 실시간 내장형 시스템에서 가장 중요한 문제들이다.
단일 코어에서의 실시간 스케줄링 연구는 1960년대부터 왕성하게 진행되어 왔으며, 어느 정도 이론이 잘 정립되어 있는 상태이다. 이에 반해, 멀티 코어에서의 실시간 스케줄링 연구는 지난 수년 동안 활발히 연구되고 있으나 아직 해결해야할 문제들이 많이 남아있다. 단일 코어의 경우에는 EDF(Earliest Deadline First)[3]와 RM(Rate Monotonic)[3]등 최적의 스케줄링 알고리즘들도 개발되었고, 이미 상용화 시스템들(예, VxWorks[4], RTLinux[5] 등)에 구현되어 많이 사용되고 있다. 하지만, 멀티 코어의 경우에는 EDF와 RM이 더 이상 최적의 스케줄링 알고리즘이 아니며, 그 성능이 현저하게 떨어진다. 이에 따라, 멀티코어의 특성을 효율적으로 활용한 다양한 스케줄링 알고리즘들이 이론적으로 개발되었다[6]-[11]. 경쟁 회피 스케줄링 기법[9]은 대표적인 멀티코어용 스케줄링 기법으로서, 기존 스케줄링 알고리즘에 추가적으로 적용 가능한 기법이다. 경쟁 회피 스케줄링 기법은 무경쟁 타임 슬롯이라는 개념을 활용한다. 하나의 타임 슬롯은 실시간 작업들이 동작하는 최소한 시간 단위를 나타낸다. 무경쟁 타임 슬롯의 가장 큰 특성은 실시간 작업들이 해당 슬롯에서 실행되는 동안은 경쟁 없이 모두 실행되는 것이 보장 된다는 것이다. 실시간 작업들은 태스크(Task)라는 작업 단위와 더 하위 작업 단위인 잡(Job)이라는 작업 단위를 가지며, 태스크는 잡을 주기적으로 반복 생성 하게 된다. 경쟁 회피 스케줄링 기법은 각각의 태스크가 잡을 생성해 낼 때마다 각 잡이 실행 하는 동안 겪을 수 있는 최소한 무경쟁 타임 슬롯의 개수를 계산한다. 그 후, 잡이 실행을 수행하는 도중 남은 실행시간과 남은 무경쟁 슬롯의 개수가 같아질 때 해당 잡의 우선순위를 최하위로 만듦으로써 다른 잡들의 실행 우선순위를 상대적으로 높게 만든다. 최하위의 우선순위를 부여 받은 잡은 남은 무경쟁 슬롯에서 경쟁 없이 실행 가능하므로 마감 시간의 준수가 보장되며, 다른 잡들은 상대적으로 우선순위가 상승하게 되므로, 전체적인 스케줄링 성능이 향상 되게 된다.
이러한 경쟁 회피 스케줄링 기법은 최신 연구를 통해 성능이 더욱 향상 되게 되었다. 앞서 말한 바와 같이, 경쟁 회피 스케줄링 기법은 무경쟁 시간 슬롯의 최소 개수를 계산하게 되는데, 이때 모든 실행 가능한 작업들의 실행 량을 예측하고 이용 가능한 시간 슬롯의 개수와의 비교를 통해 이를 계산하게 된다. 최신 연구에서 제안 된 다중 계층 경쟁 회피 스케줄링 기법[12]을 통해 실행 량의 예측에 있어서 더욱 정확한 계산이 가능해 졌으며, 이를 통해 더욱 많은 무경쟁 시간 슬롯의 확보가 가능해 졌다. 이는 곧 더욱 많은 실시간 작업들이 무경쟁 상태에서 실행이 가능해짐을 의미하므로, 스케줄링 알고리즘의 성능이 더욱 향상 되게 된다. 다중 계층 경쟁 회피 스케줄링 기법은 그 우수한 성능에도 불구하고 오직 EDF에만 적용되었다.
본 논문에서는 다중 계층 경쟁 회피 스케줄링 기법을 RM 스케줄링 알고리즘에 적용하고 이를 위한실시간성 분석 기법을 제안한다. 또한, 자체 개발한 자바(Java) 기반의 시뮬레이터를 이용하여 프로세서의 개수와 다중 계층 회피 기법의 계층 높이에 따른 RM의 성능 향상 정도를 분석한다. 2장에서는 본 연구에서 가정하는 시스템 모델과 기본 개념들을 설명한다. 3장에서는 다중 계층 회피 스케줄링 기법이 적용 된 RM에 대해 설명하고, 4장에서는 이를 위한 실시간성 분석 기법을 제안한다. 5장에서는 자체개발한 시뮬레이터를 통해 제안된 기법의 성능을 분석하며, 6장에서는 결론을 맺는다.
Ⅱ. 시스템 모델
본 논문은 태스크 집합 τ={τi}을 고려한다[11]. 태스크 τi 는 잠재적으로 무한히 많이 발생할 수 있는 일련의 잡들을 표현한다. 각 태스크 τi는 (Ti, Ci, Di)로 표현할 수 있고, 양의 부호 실수 (Positivereal Number) Ti 는 잡들 간의 최소 분리 시간(혹은 주기(Period))을, 양의 실수 Ci 는 하나의 잡의 최대 실행시간, 양의 실수 Di 는 하나의 잡의 생성시간과 마감시간의 간격을 의미한다. 본 논문에서는 각 태스크의 잡 생성 시간에 대한 상대적인 마감시간은 주기와 동일하고(즉, Ti=Di), 멀티 프로세서 환경을 가정한다. 시간 슬롯은 잡들이 동작하는 최소한 시간 단위를 나타내며, 하나의 잡은 하나의 시간 슬롯에서 최대 하나의 프로세서에서만 동작함을 가정한다.
본 논문에서는 RM 스케줄링 알고리즘을 고려한다. RM 스케줄링 알고리즘은 주기가 짧은 태스크에게 높은 우선순위를 부여하며, 동일한 태스크로부터 생성된 잡들은 동일한 실행 우선순위를 가지게 된다. RM에 N계층의 경쟁 회피 스케줄링 기법이 적용 되었을 경우 RM-CFN로 나타낸다. 무경쟁 시간 슬롯은 프로세서의 개수(m)보다 현재 실행 대기 중인 잡들의 개수가 작거나 같은 시간 슬롯으로 정의된다. 해당의 정의에 의해 모든 실행 대기 중인 잡들은 실행이 보장 되게 된다.
Ⅲ. RM을 위한 다중 계층 경쟁 회피 스케줄링기법 적용
3.1 알고리즘
먼저 RM의 스케줄링 패턴에 대해 설명 한 후 다중 계층 경쟁 회피 기법이 적용된 RM의 스케줄링방법에 대해 설명 한다.
그림 1은 세 개의 태스크 τ1(9, 4, 8), τ2(9, 3, 8), τ3(23, 14, 22)가 두개의 프로세서를 가지는 시스템에서 RM에 의해 스케줄링 되는 패턴을 나타낸다. RM은 짧은 주기를 가지는 태스크에게 높은 실행 우선순위를 부여하므로 τ1 와 τ2 는 τ3 보다 높은 실행 우선순위를 가지게 된다. 따라서 τ1 와 τ2 가 생성해 내는 모든 잡들은 τ3 가 생성해 내는 모든 잡들보다 높은 우선순위를 가지게 된다. 그림에서 볼 수 있듯이 0부터 3 사이의 시간 슬롯에서 τ1 와 τ2 의 첫 번째 잡들이 실행이 되며, τ2 의 잡이 실행을 끝난 후에 τ3 의 잡이 실행을 시작하게 된다. 12 이후의 시간 슬롯부터는 τ1 와 τ2 의 두 번째 잡들이 생성되어 우선순위를 가지며 실행을 하게 되며, τ3 의 잡은 15 이후의 시간 슬롯에서 실행을 재개하여 자신의 마감시간 이전에 실행을 끝마치게 된다.
다중 계층 경쟁 회피 기법은 각각의 테스크들이 생성해 내는 잡들을 다루기 위해 N+1개의 큐를 사용한다. 각각을 QN, QN-1, ... , Q1, Q0으로 표기한다. 이 큐들은 잡들의 우선순위를 계층화 시키는 용도로 사용되는데, QN에 존재하는 잡들은 QN-1에 존재하는 잡들보다 항상 높은 우선순위를 가지게 된다. 그리고 하나의 잡이 생성 될 때 마다 그 잡의 마감시간 전에 존재할 수 있는 무경쟁 시간 슬롯의 개수를 계산하게 되는데, 이것은 N개의 계층을 가지게 된다. 태스크 τi 로부터 생성된 잡들이 가지는 N개의 서로 다른 계층의 무경쟁 시간 슬롯의 개수를 로 나타낸다. 하나의 잡이 시간 슬롯에서 실행을 하게 되면 요구되어진 실행시간이 감소하게 되는데, 해당 시간 t에서 남아 있는 실행시간을 Ci(t)로 표기한다. 무경쟁 시간 슬롯에서 실행될 경우 최초 계산 된 무경쟁 시간 슬롯의 개수에서 1만큼 차감 되게 되는데, 해당 시간 t에서의 남아 있는 무경쟁 시간 슬롯의 개수를 로 표기한다.
그림 2는 다중계층 경쟁 회피 스케줄링 기법의 동작을 나타낸다. 각각의 시간 슬롯에 대해 하나의 테스크 τi 가 하나의 잡을 생성할 때, 이 잡을 QN에 넣는다. 그리고 해당 잡에 해당되는 N개의 서로 다른 계층의 무경쟁 시간 슬롯()을 구하고, 잔여 실행시간 Ci(t)과 잔여 무경쟁 시간 슬롯()의 개수를 각각 Ci 와 로 초기화 시킨다(라인 1~3). N 개의 서로 다른 큐에 존재하는 잡들에 대해 해당 잔여 실행시간 Ci(t)과 잔여 무경쟁 시간 슬롯()을 비교한다. 만약 시간 t에서 Qx(N≥x≥1)에 존재하는 잡의 잔여 실행시간 Ci(t)이 보다 작거나 같다면 해당 잡을 Qx-1로 이동시킨다(라인 4~10). 각각의 잡들에 대해 현재 시간 슬롯이 x계층(N≥x≥1) 무경쟁 시간 슬롯이면, 을 1만큼 감소시킨다(라인 11-15).
마지막으로 각각의 큐에 존재하는 잡들 중 m개 만큼 선택하여 RM 스케줄링을 이용하여 실행시키게 되며, 선택 된 잡들의 잔여 실행시간 Ci(t)은 1만큼 차감된다. 이때, 앞서 말한 바와 같이 QN에 존재하는 잡들은 QN-1에 존재하는 잡들보다 높은 우선순위를 가지게 되므로, 높은 우선순위 큐에 존재하는 잡들이 우선적으로 선택되어 RM으로 실행 되게 된다.
3.2 무경쟁 시간 슬롯 계산
앞서 살펴본 바와 같이 다중 계층 경쟁 회피 스케줄링 기법은 생성 된 잡들의 잔여 실행시간과 잔여 무경쟁 시간 슬롯의 개수를 비교하여 우선순위를 한 단계씩 낮추면서 다른 잡들의 실행 우선순위를 높이게 된다. 이번 장에서는 왜 그러한 기법이 우선순위가 낮아진 잡들의 마감시간준수를 보장하는지와 N개의 서로 다른 계층의 무경쟁 시간 슬롯을 구한 방법에 대해 알아본다. 먼저 단일 계층에 대한 무경쟁 슬롯 개수의 계산 방법을 설명 한 뒤 다중 계층으로 확장 되는 방법을 설명한다.
잡마다 고유한 무경쟁 슬롯의 개수를 가지게 되며, 잡이 해당 태스크로부터 생성 될 때마다 계산되어 지게 된다. 기본적인 방법은 하나의 잡이 생성되는 시간과 그 잡의 마감시간 사이에 얼마나 많은 실행 로드들이 존재할 것인지 분석하고, 활용 가능한 시간 슬롯에 모든 실행 로드들이 최대한 실행을 위해 경쟁을 한다고 가정하여, 잡들이 실행을 위해 경쟁해야 하는 최대한의 시간 슬롯을 구하는 것이다. 우리는 이 시간 슬롯을 경쟁 시간 슬롯이라고 하며, 존재 하는 시간 슬롯에서 최대한의 경쟁 시간 슬롯을 제외시키면 최소한의 무경쟁 시간 슬롯의 양을 구할 수 있다.
그림 3은 태스크 τk 가 생성한 잡의 생성시간과 마감시간 사이에 태스크 τi 가 생성한 잡들의 최대 실행 로드가 발생할 수 있는 시나리오를 나타낸다[14]. 즉, 태스크 τk 가 생성한 잡의 생성시간과 마감시간 사이의 간격은 Dk 이므로 Dk 의 길이를 가지는 구간사이에서 발생 가능한 최대 실행 로드이다.
그림 3에서 보는 바와 같이 가장 왼쪽 잡의 실행은 Dk 구간의 시작에서 시작되며, 해당 잡의 마감시간에 종료된다.
가장 오른쪽 잡의 실행은 해당 잡의 생성 시간에서 시작되며 대기시간 없이 계속 실행 되게 된다. 그림 3을 통해 Dk 구간 안에서 Ci 만큼 실행하는 테스크 τi 가 생성한 잡들의 개수는 다음과 같이 계산 가능하다.
| (1) |
그림 3의 시나리오를 예로 들 경우, 식 (1)에 의해 계산된 값은 2가 되며, 가장 왼쪽의 잡과 중간의 잡이 Ci 만큼 실행하는 태스크 τi 가 생성한 잡들이다. 이를 값을 이용하고 더불어 Ci 만큼 실행하지 못하는 잡(그림 3의 가장 오른쪽 잡)의 최대 실행 로드는 계산하면 다음식과 같이 Dk 구간에서의 최대 실행 로드 Wi(Dk)를 계산할 수 있다
| (2) |
우리는 m개의 프로세서를 가정하므로 Dk 구간 안에는 m∙Dk 크기의 실행 가능한 시간 공간이 존재한다. 식 (2)를 이용하여 m∙Dk 크기의 공간 안에 모든 잡들의 최대 실행 로드들을 밀어 넣음으로써 최대한의 경쟁 시간 슬롯을 구할 수 있다. 이를 바탕으로 존재 가능한 시간 슬롯에서 구해진 경쟁 시간 슬롯을 제외시키면 최소한의 무경쟁 시간 슬롯을 계산 할 수 있다. 하나의 시간 슬롯에 m개의 잡들이 실행을 위해 존재한다면 추가적인 잡들은 불가피 하게 m개의 잡들과 경쟁을 하게 된다. 따라서 Dk 구간에서의 경쟁 시간슬롯은 다음과 같이 구할 수 있다.
| (3) |
이를 이용하여 태스크 τk 가 생성한 잡의 생성시간과 마감시간 사이에 존재하는 최소한의 무경쟁 시간 슬롯의 개수 Φk는 다음과 같이 계산 가능하다.
| (4) |
식 (4)에서 태스크 τk의 경우 식 (3)을 적용 시키지 않고 대신 Ck 만큼만 실행됨을 가정함으로써 식 (4)의 계산을 더욱 유리하게 만들었다. 이는 다른 잡들과는 다르게 태스크 τk 가 생성한 잡의 경우 Dk 구간은 해당 잡의 생성시간과 마감시간을 의미하므로, 이 구간에서 하나의 잡만이 생성되는 것이 항상 보장되기 때문이다.
식 (4)를 다중 계층 경쟁 회피 스케줄링 기법에 적용하기 위하여 단일 계층 경쟁 회피 스케줄링 기법에서의 잡들의 동작을 살펴보자. 단일 계층 경쟁 회피 스케줄링 기법에서는 두 개의 큐 Q1, Q0가 사용되며, 각 잡의 잔여 실행시간 Ci(t)이 잔여 무경쟁 시간 슬롯의 개수보다 작거나 같아지는 순간 Q1에서 Q0로 이동 되게 된다. 이때, Q1에 있는 작업은 Q0에 있는 잡들보다 높은 우선순위를 가지게 된다. τi 가 생성한 잡이 t′의 시간에 Q1에서 Q0로 이동하였다고 가정하자. 식 (4)에 의해 태스크 τi 가 생성한 잡의 생성시간과 마감시간 사이에 최소한 Φi개의 무경쟁 타임 슬롯에 존재 하므로, τi가 생성한 잡은 Q1에서 Q0로 이동하기 전 Φi - Φi(t′) 만큼의 무경쟁 슬롯에서 실행되었다. 또한, 잔여 실행시간 Ci(t)이 잔여 무경쟁 시간 슬롯의 개수보다 작거나 같아지는 순간 Q1에서 Q0로 이동하므로 남은 실행 량은 Φi(t′)보다 작거나 같다. 따라서 단일 계층 경쟁 회피 스케줄링 기법 하에서는 적어도 τi 가 생성한 잡의 Φi 만큼의 실행 량은 Q1에 존재하는 다른 잡들을 방해 하지 않게 된다.
이중 계층 경쟁 회피 스케줄링 기법은 단일 계층 경쟁 회피 스케줄링의 이러한 특성을 활용하여, 경쟁 시간 슬롯의 계산 시에 모든 잡들의 실행 로드에서 Φi 만큼 차감하여 계산하게 된다. 이러한 특성은 더 높은 계층의 경쟁 회피 스케줄링에 반복적으로 적용할 수 있으며, N계층의 경쟁 회피 스케줄링의 기법의 적용 시에는 각 잡들의 실행 로드에 대해 만큼의 차감시켜 경쟁 시간 슬롯의 개수를 구하게 된다. 즉, 를 구하기 위해서는 의 순으로 N번의 계산을 거쳐야 한다. 이것을 식으로 나타내면 다음과 같다.
| (5) |
여기서 는 를 나타낸다(N≥x≥1). 따라서 식 (2), (3), (4)도 아래와 같이 확장되게 된다.
| (6) |
| (7) |
| (8) |
Ⅳ. 다중 계층 경쟁 회피 스케줄링 기법이적용된 RM을 위한 실시간성 분석 기법
이전 장에서는 다중 계층 회피 스케줄링 기법이 적용된 RM의 동작 방법을 제안하였다. 이 장에서는 다중 계층 회피 스케줄링 기법이 적용된 RM을 위한 실시간성 분석 기법을 제안한다. 실시간성 분석 기법은 시스템이 해당 스케줄링 알고리즘에 의해 동작할 때 모든 작업들이 마감시간 내에 동작을 끝마칠 수 있는지 설계단계에서 수학적으로 분석하는 기법이다. 수많은 실시간성 분석 기법 중 방해 시간 기반 실시간성 분석 기법[12]을 제안한다. 방해 시간 기반 실시간성 분석은 각각의 태스크에 대해 이루어지며, 먼저 각 태스크가 생성하는 잡이 겪을 수 있는 최대 방해시간을 계산한다. 구해진 최대 방해시간에 자신의 최대 실행시간(Ci)을 더한 후 이 값이 태스크의 마감시간(Di)보다 작다면, 생성 될 모든 잡들이 항상 마감시간 내에 종료됨을 보장하게 된다. 이 작업을 모든 태스크에 대해 한번씩 수행하게 되며, 모든 태스크가 자신이 생성한 모든 잡들이 마감시간 내에 종료됨을 보장하게 된다면, 시스템 자체에서 마감시간의 위반이 없음을 보장하게 된다.
먼저, 각 태스크 τk가 생성하는 잡들이 실행 중에 겪을 수 있는 최대 방해 시간을 구해야 하는데, 이는 2.2장에서 유도 하였던 최대 실행 로드의 계산 값을 이용한다. Wi(Dk)는 Dk구간에서 발생 가능한 τi가 생성한 잡들의 최대 실행 량이다.
그림 4에서 볼 수 있는 바와 같이, 이중 최대 Dk-Ck+1 만큼만 계산하게 된다. 나머지는 τk와 같은 시간에 실행되므로, τk를 방해 할 수 없기 때문이다. 또한, RM에 의해 τk는 높은 우선순위를 가지는 태스크들로부터만 실행의 방해를 받으므로 높은 우선순위를 가지는 태스크들로 부터의 실행 량만 계산하게 된다. 이 논문에서는 N계층의 경쟁 회피 스케줄링 기법을 고려하고 있으므로, 식 (7)을 확장하여, τk 가 생성하는 잡들이 겪을 수 있는 최대 방해 시간을 다음과 같이 구할 수 있다.
| (9) |
여기서, τhp(k)는 τk보다 높은 우선순위를 가지는 태스크 집합을 나타낸다. 그림 4에서 볼 수 있듯이, 식 (9)의 값이 Dk-Ck+1보다 크게 되면 Dk 구간 내에서 τk가 생성한 잡이 Ck만큼 실행함을 보장 할 수 없게 된다. 따라서 아래의 식을 만족하면 τk가 생성하는 모든 잡들은 N계층 경쟁 회피 스케줄링 기법이 적용 된 RM에 의해 마감시간이 준수됨을 보장 받게 된다.
| (10) |
Ⅴ. 실 험
이번 장에서의 본 논문에서 제안한 다중 계층 경쟁 회피 스케줄링 기법이 적용된 RM의 실시간성 분석 기법의 성능과 기존에 제안 되었던 다중 계층 경쟁 회피 스케줄링 기법이 적용된 EDF[12]의 성능을 비교 평가 한다. 성능의 평가를 위해 자체 개발 한 Java 기반의 시뮬레이터를 사용하며, 기존에 널리 알려진 태스크 집합 생성기법[15][16]을 바탕으로 임의로 생성 된 태스크 집합을 이용한다.
이 태스크 집합 생성 기법은 태스크 집합 τ에 대해 두개의 입력 인자, 프로세서 개수 m∈{2, 4, 8, 16}, 태스크의 프로세서 이용률(Ci/Ti) 분산 (입력인자 p∈{0.1, 0.3, 0.5, 0.7, 0.9}를 갖는 이봉분포 또는 지수분포)을 고려한다. 또한, 각각의 태스크 τi에 대해 다음과 같은 입력 인자를 갖는다. Ti는 1과 1000사의 수중 임의의 값으로 결정되며, Ci는 태스크 집합의 입력인자에서 정해진 이봉분포 또는 지수분포를 따른다. 마지막으로 Di는 Ti와 정해진 Ci사이의 값 중 임의의 수로 결정 된다. 성능 지표로서 임의로 100,000개의 태스크 집합 중 식 (10)을 만족하는 태스크 집합의 개수를 파악한다. 다중 계층 회피 스케줄링 기법의 계층에 따른 RM의 실시간성 분석 기법의 향상 정도를 분석하기 위해 RM, RM-CF1, RM-CF5를 고려하고 기존 기법인 EDF, EDF-CF1, EDF-CF5과의 비교를 통해 본 논문에서 제안한 기법을 통한 성능 향상에 대해 분석한다.
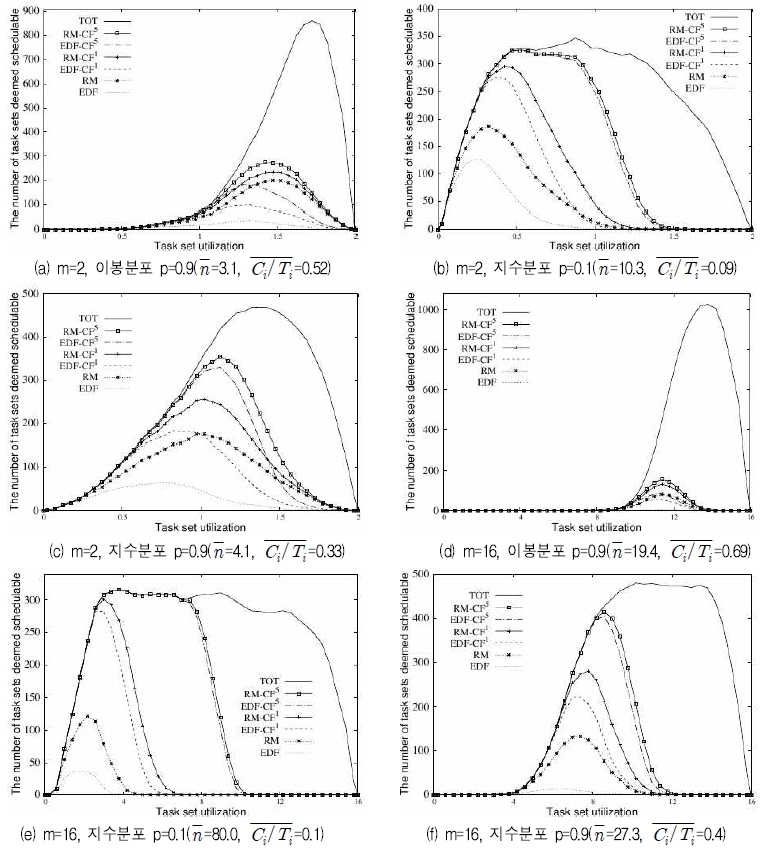
그림 5는 서로 다른 프로세서 개수 (m=2, 16)와 서로 다른 태스크의 프로세서 이용률 분산에 대한 각 실시간성 분석 기법의 성능 평가 결과를 나타낸다. 각각의 생성한 태스크의 프로세서 이용률을 가지는 태스크 집합들에 대해 각 실시간성분석 기법들이 얼마나 많은 태스크 집합들의 실시간성을 보장 하는지 측정 하였다. 그림에서 TOT는 해당 태스크의 프로세서 이용률에 해당 되는 총 생성 된 태스크 집합 개수를 나타낸다. 서로 다른 태스크의 프로세서 이용률 분산에 따라 생성된 각각의 태스크 집합은 서로 다른 평균 태스크 개수와 태스크의 프로세서 이용률 평균을 가지게 되는데, 이를 각각 와 로 나타낸다.
실험결과에서 볼 수 있듯이 모든 경우에 대해, 경쟁 회피 스케줄링 기법의 계층이 상승 할수록 성능도 상승함을 알 수 있다. 특히, p = 0.1의 입력인자를 가지는 지수 분포의 경우 (그림 5(b)와 그림 5(e)) 다중 계층 경쟁 회피 스케줄링 기법에 의한 성능 향상이 가장 높음을 볼 수 있다. 이는 태스크의 평균 프로세서 이용률이 가장 낮기 때문에 각 태스크가 가지는 무경쟁 시간 슬롯의 개수가 많으며, 이로 인하여 다중 계층 경쟁 회피 스케줄링 기법의 성능이 향상되기 때문이다. 반대로, p = 0.9의 입력인자를 가지는 이봉 분포의 경우 태스크의 평균 프로세서 이용률이 가장 높으며 다중 계층 회피 스케줄링 기법에 의한 성능 향상이 가장 낮음을 볼 수 있다.
또한, 동일한 태스크의 프로세서 이용률 분산 (즉, 동일한 와 )과 동일한 경쟁 회피 스케줄링 기법의 계층 (예를 들어, RM-CF1 vs. EDF-CF1 또는 RM-CF5 vs. EDF-CF5)에 대해 RM이 EDF보다 항상 높은 성능을 보인다는 것을 알 수 있다. 이것은 적용된 경쟁 회피 스케줄링 기법의 계층 높이와 상관없이 RM의 실시간성 분석기법은 하나의 태스크에 대한 분석을 수행할 때 그 태스크의 우선순위보다 낮은 태스크는 계산에서 제외시키는 반면 (식 (9)에서 볼 수 있듯이), EDF의 경우 우선순위와 상관없이 모두 포함시키기 때문이다.
하지만 이러한 이점은 적용 된 경쟁 회피 스케줄링 기법의 계층이 상승 할수록 작아지게 되어 RM와 EDF의 성능 차이가 줄어들게 된다.
예를 들어 그림 5(f)의 경우 RM-CF1과 EDF-CF1는 상대적으로 큰 성능 차이를 보이는 반면, RM-CF5과 EDF-CF5는 매우 근사한 성능을 보인다. 이것은 RM 고유의 실시간성 분석 기법에서는 오는 이점보다 높은 계층의 경쟁 회피 스케줄링 기법에서 오는 이점이 커지기 때문이다.
마지막으로 관찰 할 수 있는 것은, 프로세서의 개수가 작을수록, 동일한 계층의 경쟁 회피 스케줄링 기법이 적용 되었을 때 RM과 EDF의 성능차이가 커진다는 것이다. 이것은 프로세서의 개수가 커질 경우 많은 수의 무경쟁 시간 슬롯이 존재하여 다중 계층 경쟁 회피 스케줄링 기법의 성능이 향상되어 RM과 EDF간의 성능차이가 줄어 들기 때문이다. 예를 들어 그림 5(c)와 그림 5(f)에서 볼 수 있듯이, 동일한 태스크의 프로세서 이용률 분산 (지수분포 p=0.9)이 적용 되었음에도 불구하고 그림 5(c)의 경우 (m=2)에서 RM과 EDF가 더 큰 성능차이를 보인다. 그림 5(c)의 경우 RM-CF1은 41942개의 태스크 집합에 대해 실시간성을 보장 한 반면, EDF-CF1는 27363개의 태스크 집합의 실시간성을 보장하였고(약, 53.2%상승) 그림 5(f)의 경우 (m=16) RM-CF1은 21339개의 태스크 집합에 대해 실시간성을 보장 한 반면, EDF-CF1는 15090개의 태스크 집합의 실시간성을 보장하였다(약, 41.3%상승)
Ⅵ. 결론 및 향후 과제
실시간 시스템은 한정 된 자원으로 마감시간을 가지는 작업들을 동시에 실행하여야 하므로, 작업들의 우선순위를 효율적으로 결정하는 실시간 스케줄링 기법과 시스템이 해당 실시간 스케줄링 기법으로 실행되었을 때 마감시간 위배 여부를 설계 단계에서 분석하는 실시간성 분석 기법은 필수적인 요소이다. RM 스케줄링 알고리즘은 우선순위의 결정 방법이 매우 간단하면서도 높은 성능을 내는 강력한 스케줄링 알고리즘으로서 그 성능 향상을 위해 많은 연구들이 진행 되어져 왔다. 본 논문에서는 최신 스케줄링 성능 향상 기법인 다중 계층 경쟁 회피 스케줄링 기법을 RM에 적용하고, 이를 지원하는 실시간성 향상 기법을 제안하였다. 자체 개발한 Java 기반의 시뮬레이터를 이용한 실험을 통해, 경쟁 회피 스케줄링 기법의 계층 변화에 따른 성능 변화를 확인함으로써, RM의 성능이 비약적으로 향상 될 수 있음을 검증 하였다. 후속 연구로서 새로운 실시간성 분석 기법을 적용함으로써 성능을 향상 시키는 방향이 있을 것이다.
Acknowledgments
이 논문은 2016년도 정부(교육과학기술부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. NRF-2016R1A6A3A11930688)
References
- Y. S. Kim, "Feasibility Study of Real-Time Programs in Linux", Journal of KIIT, Vol. 10(No. 8), p127-134, Aug.), (2012.
-
J. H. Lee, and J. K. Choe, "A Study on Self-localization for Autonomous Mobile Robot", Journal of KIIT, Vol. 11(No. 12), p29-34, Dec.), (2013.
[https://doi.org/10.14801/kiitr.2013.11.12.29]

-
C. Liu, and J. Layland, "Scheduling algorithms for multiprogramming in a hard-real-time environment", Journal of the ACM, Vol. 20(No. 1), p46-61, Jan.), (1973.
[https://doi.org/10.1145/321738.321743]

- VxWorks, "http://www.windriver.com/products/vxworks/" [Accessed: Dec. 01, 2017].
- RTLinux, "http://www.rtlinuxfree.com/" [Accessed: Dec. 01, 2017].
- S. K. Lee, "On-line multiprocessor scheduling algorithms for real-time tasks", Region 10's Ninth Annual International Conference, IEEE, p607-611, Aug.), (1994.
-
S. Baruah, N. K. Cohen, C. G. Plaxton, and D. A. Varvel, "Proportionate progress: a notion of fairness in resource allocation", Algorithmica, Vol. 15(No. 6), p600-625, Jan.), (1996.
[https://doi.org/10.1007/s004539900032]

-
J. Y.-T. Leung, "A new algorithm for scheduling periodic, real-time tasks", Algorithmica, Vol. 4, p209-219, Jan.), (1989.
[https://doi.org/10.1007/bf01553887]

-
Hoon Sung Chwa, Hyoungbu Back, Sanjian Chen, Jinkyu Lee, Arvind Easwaran, Insik Shin, and Insup Lee, "Extending Task-level to Job-level Fixed Priority Assignment and Schedulability Analysis Using Pseudo-deadline", Real-Time Systems Symposium, IEEE, San Juan, Puerto Rico, Dec.), (2012.
[https://doi.org/10.1109/rtss.2012.58]

-
Hyeongboo Baek, Hoon Sung Chwa, and Jinkyu Lee, "Beyond Implicit-Deadline Optimality: A Multiprocessor Scheduling Framework for Constrained-Deadline Tasks", Real-Time Systems Symposium, Paris, IEEE, France, Dec.), (2017.
[https://doi.org/10.1109/rtss.2017.00038]

-
Jinkyu Lee, Arvind Easwaran, and Insik Shin, "Contention-Free Executions for Real-Time Multiprocessor Scheduling", Transactions on Embedded Computing Systems, ACM, Vol. 13(No. 2s), Article 69 p1-25, Jan.), (2014.
[https://doi.org/10.1145/2494530]

-
Hyeongboo Baek, Jinkyu Lee, and Insik Shin, "Multi-Level Contention-Free Policy for Real-Time Multiprocessor Scheduling", Journal of Systems and Software, Vol. 137, p36-49, Mar.), (2018.
[https://doi.org/10.1016/j.jss.2017.11.027]

- A. Mok, "Fundamental design problems of distributed systems for the hard-real-time environment", Ph. D. thesis, Massachusetts Institute of Technology, May), (1983.
-
M. Bertogna, M. Cirinei, and G. Lipari, "Schedulability analysis of global scheduling algorithms on multiprocessor platforms", Transactions on Parallel and Distributed Systems, IEEE, Vol. 20(No. 4), p553-566, Jul.), (2009.
[https://doi.org/10.1109/tpds.2008.129]

- T. P. Baker, "Comparison of empirical success rates of global vs. partitioned fixed-priority EDF scheduling for hard real-time", Technical report, TR–050601, Department of Computer Science, Florida State University, Tallahassee, Aug.), (2005.
-
B. Andersson, K. Bletsas, and S. Baruah, "Scheduling arbitrary-deadline sporadic task systems on multiprocessor", International Conference on Embedded and Real-Time Computing Systems and Applications, IEEE, p197-206, Dec.), (2008.
[https://doi.org/10.1109/rtss.2008.44]


2010년 2월 : 건국대학교 컴퓨터공학과(공학사)
2012년 2월 : 한국과학기술원 전산학과(공학석사)
2016년 8월 : 한국과학기술원 전산학과(공학박사)
2016년 8월 ~ 현재 : 성균관대학교 박사 후 연구원
관심분야 : 실시간 시스템, 사이버 물리 시스템