모폴로지 특성 분석 방법을 이용한 충돌성 잡음 제거 기법


초록
본 연구에서는 모폴로지 특성 분석 방법을 이용하여 충돌성 잡음이 섞인 음성으로부터 잡음을 제거하는 알고리즘을 제안한다. 음성신호를 정상신호라고 가정하면, 충돌성 잡음은 음성 신호보다 그 지속시간이 매우 짧은 신호이다. 모폴로지 성분 분석은 두 종류의 신호가 혼합된 신호에 대해서 한쪽 신호만을 스파스 공간으로 하고, 다른 신호는 비스파스 공간으로 표현하는 두 종류의 기저계를 이용하여 신호를 분리하는 방법이다. 그러나 충돌성 잡음은 그 지속 시간만을 가지고 특정한 기저계로 정의하는 것은 불가능하다. 따라서 기저계를 변형하여 시작 시간이 다르고, 또한 지속 시간이 짧은 신호의 부분 공간을 복수개로 정의한 다음, 잡음을 근사화하고, 음성 신호는 DFT 기저계를 이용하여 근사화를 수행한다. 신호는 DFT 기저와 잡음 신호의 부분 공간에 관한 스파스 코스트 함수로 분해한다. 컴퓨터 시뮬레이션에서는 여러 종류의 충돌성 잡음에 대하여 제안한 방법을 적용하여 그 유효성을 확인하였다.
Abstract
In this paper, we propose a separation method using Morphological Component Analysis(MCA) for mixtures which consist of speeches and impact noises. We assume that the speech is stationary within a short period of time and the duration of the noises is shorter than the period. MCA is a separation method for signal mixtures using a pair of dictionary which can yield a sparse representation for signal but not appropriate for other. However, it is difficult for impact noises to define specific base because the only assumption of noises if that its durations are relatively short. Then, we represented impact noises with subspaces that consists of signals whose durations are restricted. Speeches are represented with DFT bases. Signals are separated by imposing a cost function of sparsity on coefficients of DFT and choice of subspace for noises. In a computer based simulation, we demonstrate the noise reduction capability of the proposed method for various impact noises.
Keywords:
noise reduction, impact noise, morphological component Analysis, DFT, speech signal processingⅠ. 서 론
잡음이 중첩된 음성신호에서 잡음을 제거하는 기술은 신호처리 분야에 있어서 매우 중요한 기술이다. 따라서 지금까지 많은 잡음 제거 알고리즘들이 제안되고 있다[1]-[3]. 이들 방법 중, 거의 대부분은 잡음 신호를 정상 신호라고 가정하여 처리하고 있다. 예를 들면, 음성 강조의 대표적인 방법인 스펙트럼 감산법(Spectral Subtraction)[1][4]은 잡음의 스펙트럼을 추정한 다음, 이것을 입력 신호의 스펙트럼에서 감산하여 잡음을 제거하고 있다. 그러나 이 방법은 잡음의 스펙트럼을 추정하기 위해서 잡음을 정상 신호라고 가정하여 처리함으로, 지속 시간이 짧은 충돌성 잡음(Impact Noise)에는 적용하기 어렵다. 따라서 충돌성 잡음을 제거하기 위한 방법들이 제안되고 있다[5]-[7]. 그러나 제안된 방법들은 잡음의 진폭 변화가 작은 것에서만 유효하고, 잡음의 지속 시간이 긴 충돌성 잡음을 제거하는 것은 어렵다고 알려져 있다.
이와 같은 충돌성 잡음을 제거하기 위하여 참고문헌[5][6][8]에서는 충돌성 잡음의 발생 구간을 추정하고 잡음이 발생한 구간에서 신호를 제거한 다음, 주위의 음성을 보간하고 있다. 그러나 이 방법은 음성이 시작될 때, 잡음이 발생할 경우, 음성이 더욱 열화된다는 문제점을 갖고 있다.
한편, 영상 신호처리 분야에서 성질이 다른 신호가 서로 혼합된 경우, 각 신호별로 분리하는 모폴로지 성분 분석(MCA, Morphology Component Analysis) 알고리즘이 제안되었다[8][9]. MCA 알고리즘에서는 분리 대상이 되는 신호를 최소한의 기저(Base)로 표현할 수 있도록 기저계를 분리 대상 별로 준비하고, 혼합된 신호를 이들 기저계를 이용하여 가능한 적은 수의 벡터의 선형 결합으로 표현함으로서 신호를 분리하고 있다[7][10]. Stark[6] 등은 이 방법을 기초로 성질이 다른 두 개의 영상이 겹친 신호에 대하여 각 영상을 스파스(Sparse)로 나타내는 두 개의 직교 기저 행렬을 이용하여 영상을 분리하는 방법을 제안하고 있다.
따라서 본 연구에서는 이와 같은 MCA 알고리즘을 이용하여 충돌성 잡음과 음성을 분리하는 방법을 제안하고자 한다. 일반적인 MCA 알고리즘은 분리 대상이 되는 신호를 스파스로 선택하는 것이 매우 중요하다. 그러나 충돌성 잡음의 경우에는 그 지속 시간만 가정할 수 있으므로 특정한 기저계를 정의하기는 매우 어렵다. 따라서 충돌성 잡음의 지속시간을 고려한 부분 공간에서 각 공간의 벡터 합으로 표현하고, 이것을 갱신시켜, 특정한 기저를 선택하지 않고, 또한 잡음이 존재하는 구간을 추정하지 않는 신호 분리 방법을 제안한다.
Ⅱ. 모폴로지 성분 분석
분리 대상이 되는 음성 신호 및 잡음 신호를 s,n∈RN이라고 할 때, 관측 신호 f∈RN는 다음식과 같이 표현할 수 있다.
| (1) |
식 (1)에서 신호 s와 n은 각각 기저 행렬 T1 및 T2을 이용하여 표시하면 다음식과 같이 된다.
| (2) |
여기서 T1 및 T2은 n × m 행렬이고, m ≥ n이라고 가정한다. 또한 식 (2)를 만족하는 c1, c2중에서 영이 아닌 요소가 희박한 벡터가 얻어졌을 때, 이것을 스파스라고 한다.
MCA 알고리즘은 s가 스파스 신호이고, n이 스파스가 아닌 T1과 n이 스파스 신호이고, s가 스파스 신호가 아닌 T2 을 알고 있다는 조건에서 관측 신호 f 에서 음성 신호 s와 잡음 n을 추정하는 방법이다. 즉, MCA 알고리즘에서는 T1과 T2를 이용하여 다음식의 해를 구하는 것이다.
| (3) |
신호 및 잡음의 추정 계수 벡터를 , 라고 하면, 식 (4)을 이용하여 s와 n의 추정 벡터를 구할 수 있다[8].
| (4) |
식 (3)에서 ∥[]T∥o 는 벡터 []T의 norm을 나타내고, 벡터 []T 의 값은 “0”이 아닌 요소 수의 최솟값과 같다. T 는 전치를 나타낸다.
이 norm을 최소화시키는 방법으로 코스트 함수로 신호를 분리하는 BP(Basis Pursuit) 알고리즘이 널리 사용되고 있다[8]. BP 알고리즘에서는 식 (3)의 []T norm을 식 (5)에 나타낸 것과 같이 c1의 norm을 이용하여 구한다.
| (5) |
실제 처리에서는 계산 코스트를 저감하기 위하여 식 (5)와 식 (6)을 이용하여 구하고 있다[6][8].
| (6) |
Ⅲ. 충돌성 잡음을 제거하기 위한 모폴로지 성분 분석
3.1 기저계와 코스트 함수
음성 신호는 정현파들의 선형적인 결합으로 표현할 수 있고, 또한 주파수 영역에서 국소적 신호라고 가정할 수 있다. 반면 지속 시간이 긴 음성에 비해, 충돌성 잡음은 지속 시간이 짧기 때문에 시간 영역에서 국소적인 신호이다. 따라서 잡음을 지속 시간이 짧은 부분 신호의 합으로 표현하면, 다음식과 같이 표현할 수 있다.
| (7) |
| (8) |
여기서 T1은 DFT의 기저이고, 이며, n(i)은 n(i) = []∈RN, 은 j ≤ (i - 1)K, j ≻ iK 에서 = 0이다. 즉, n(i)는 (i - 1)K + 1번째 샘플에서 시작해서 K 샘플의 지속 시간만 갖는 신호이다. 이 부분 신호에 스파스 성질을 도입하기 위하여 식 (5)에 대응한 목적 함수는 다음식과 같이 나타낼 수 있다.
| (9) |
식 (9)을 이용하여 s와 n을 분리한다. 단, 여기서 ∥a∥0는 벡터 a의 “영”이 아닌 요소수를 나타내고, α는 코스트 함수의 가중치를 나타내고 있다. 이것을 BP 알고리즘과 같은 방법으로 각 norm을 합하면, 다음 식이 얻어진다.
| (10) |
3.2 분리 알고리즘
본 연구에서는 식 (10)의 해를 구하기 위해 BP 알고리즘의 근사 해를 구하는 방법인 BCR(Block Coordinate Relaxation) 알고리즘을 이용하였다[6].
이 알고리즘은 우선 일정한 반복 회수를 설정하고, 반복 과정에서 λ 값이 거의 “0”이 될 때까지 식 (10)의 해를 구하는 것이다. 즉, 반복 회수를 R로 하고, λ의 초기값을 λ0로 하였을 때, 다음과 같은 과정을 반복 수행한다.
(1) 추정 벡터 n(i)에서 오차 신호를 계산한다.
| (11) |
(2) 추정 벡터 을 계산하고, j번째의 요소를 다음 식을 이용하여 갱신한다.
| (12) |
(3) 갱신된 추정 벡터 c1을 이용하여 오차신호를 재계산한다.
| (13) |
(4) 잡음의 추정 벡터 을 다음 식을 이용하여 구한다.
이 추정 벡터의 norm은 다음 식과 같이 역치 처리 방식을 이용하여 갱신한다.
| (14) |
(5) 마지막으로 λ를 λ - λ0/I로 갱신한 다음, 재귀적으로 처리한다.
실제 잡음 제거 처리 알고리즘에서는 입력 신호를 프레임 별로 분리하고, 각 음성 프레임에 이 알고리즘을 적용한다. 기존의 스펙트럼 감산법과 동일하게 프레임은 프레임 길이의 1/2씩 쉬프트 시켜 오버랩하였다. 또한 스펙트럼 감산 방법에서는 창함수를 건 다음, 잡음 제거 처리를 하고 있지만, 이와 같이 하면 DFT의 주파수 분해능을 저하시켜 잡음 제거 성능을 악화시킬 위험성이 있다. 그러므로 본 연구에서는 각 프레임 사이에서 발생하는 주파수 파형의 불연속성을 피하기 위하여 처리 후에 Hanning 창을 적용하고, 전 프레임 출력과 가산시켜 처리하였다.
3.3 파라메타 값 추정
제안한 방법에서 사용하는 몇 가지 파라메타가 있다. 그것은 잡음 신호의 부분공간에 대한 지속 시간을 결정하는 파라메타 K, 음성의 푸리에 기저와 잡음의 부분 신호 선택에 대한 가중치 파라메타 α이다. 만약 이 파라메타 중, K 값이 크면, 충돌성 잡음 성분이나 음성 성분도 지속 시간이 긴 성분의 부분 공간으로 표현되기 때문에 오히려 음성의 열화가 발생하게 된다. 또한 α 값이 너무 작으면, 음성의 스파스 표현을 너무 중시하는 것이 되기 때문에 음성 열화가 발생된다.
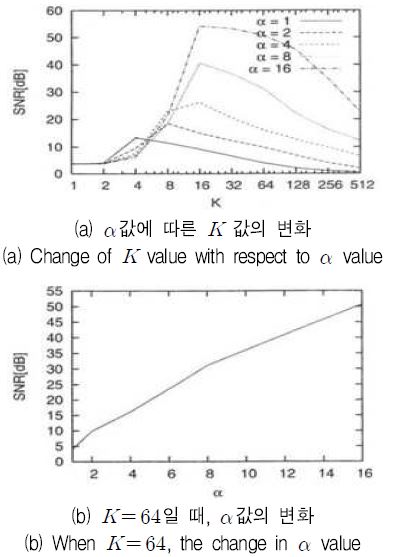
따라서 음성의 열화 정도를 확인하기 위하여 잡음이 전혀 섞여 있지 않은 깨끗한 음성에 대하여 K와 α 값을 변화시켜 가며 알고리즘을 실행하였을 때의 SNR의 변화 값을 그림 1에 제시하였다. 시뮬레이션이 사용한 음성의 샘플링 주파수는 16kHz이고, 처리하는 프레임 길이는 N = 1024이며, 초기 추정 벡터는 최소제곱법을 이용하여 λ0를 초기 추정 벡터 요소의 절대 값의 평균으로 설정하였고, R = 50회 반복 실행하였다.
잡음 제거 능력에 따라 각 파라메타의 값을 선정하기 위하여 음성 열화가 SNR 20dB에서 K 값은 가능한 크게, α 값은 가능한 작은 값을 선택하여야 한다. 컴퓨터 시뮬레이션 결과, K = 64, α = 6일 때, 음성 열화가 최소가 되었다.
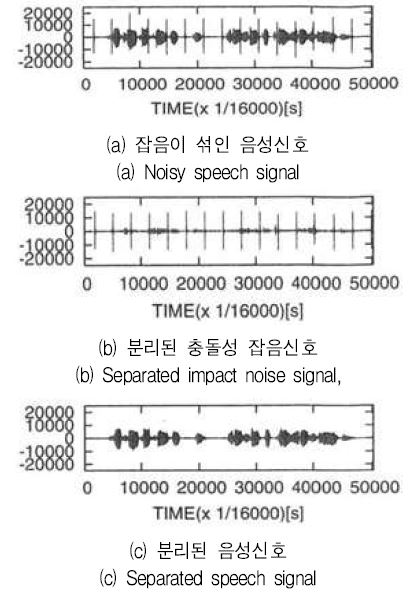
이 값을 이용하여 돌발성 잡음의 제거를 실행한 결과를 그림 2에 제시하였다.
시뮬레이션에 사용한 음원은 샘플링 주파수가 16kHz, 16비트, 모노 음원으로 윈도우 PCM 형식으로 “Norah Jones - Turn Me On" 노래의 일부분이다. 또한 잡음 신호는 음성신호와 동일한 조건의 음성 데이터베이스에 수록되어 있는 손뼉 음(Clap)을 0.2초의 일정한 간격으로 SNR이 9dB가 되도록 반복 중첩하였다. 그림 2에서 가로축은 시간을 나타내고, 세로축은 크기를 나타낸다. 또한 그림의 제일 위는 잡음이 중첩된 신호, 가운데는 제안한 알고리즘을 적용하여 분리한 잡음 신호를 나타내었고, 마지막 그림은 음성 신호를 나타내었다. 이 결과를 보면, 신호와 잡음이 적절하게 분리되고 있음을 확인할 수 있다.
Ⅳ. 시뮬레이션 및 결과 고찰
제안한 방법으로 돌발성 잡음의 분리 효과를 확인하기 위하여 음성에 여러 가지 종류의 잡음을 중첩하여 시뮬레이션 하였다.
표 1에 실험에 사용된 잡음을 제시하였다. 잡음의 지속시간이 0.2초 이하인 신호 4종류와 지속시간이 0.5초 이상인 신호 5종류이다. 여기서 지속 시간이라는 것은 발생한 신호 진폭이 최대 –40dB까지 감소할 때까지를 말한다.
처리 결과 평가는 SNR, SNR(SegSNR), 대수 스펙트럼 왜곡(LSD) 3개를 사용하였다. 즉, 이상적인 값을 x, 추정 값을 , 신호 길이를 L로 하였을 때, SNR은 다음 식을 이용하였다.
| (15) |
또한, SegSNR은 다음 식을 이용하였다.
| (16) |
충돌성 잡음은 짧은 시간에 발생 소멸하기 때문에 심하게 변화하는 신호이다. 따라서 충돌성 잡음을 제거하는 성능을 평가하기 위해서는 SegSNR의 한 프레임 길이 L을 잡음 발생 시간과 동일하게 설정하여 평가하는 것이 좋다. 따라서 평가 구간에서 SNR은 T(x) = min[max(x,- 10),35]로 하였다.
LSD는 주파수 영역에서 다음 식을 이용하였다.
| (17) |
여기서 Cl(k)는 max[|Xl(k)|2,δ]이고, δ는 10-50/10maxk,l|Xl(k)|2이다. X는 x의 스펙트럼을 나타낸다.
표 2에 각 잡음을 중첩한 신호들의 처리 전후의 SNR, SegSNR, LSD을 평균값으로 나타내었다. 잡음의 발생 간격은 0.2초이고, 전체의 SNR이 9dB가 되도록 중첩하였다. 또한 표 3에 동일한 9dB SNR, 잡음 발생 간격을 0.5초로 하였을 경우의 결과를 제시하였다.
표 2의 실험 결과를 보면, 지속 시간이 짧은 잡음의 경우, SNR이 5~9dB, SegSNR에서도 동일하게 5~9dB, LSD는 2dB 정도 향상되었다. 따라서 제안한 방법이 충분한 잡음 제거 효과가 얻어졌다는 것을 알 수 있다.
반면, 표 3과 같이 지속 시간이 긴 잡음에 관하여는 유효할 만큼 향상이 보이지 않는 잡음도 있다. 그 원인은 잡음의 지속 시간이 긴 협대역 신호가 DFT 기저에 의해 표현되어 스파스가 최대화되었기 때문이라고 생각되고, 중첩된 잡음의 파워가 작아 제거되지 않았던 잡음의 영향 때문이라고 생각된다.
또한 표 3을 보면, 발생 간격을 짧게 변화시켜도 잡음 제거 결과가 거의 변화가 없었으나, 지속 시간이 0.2초 이하인 잡음에는 더욱 제거 효과가 있음을 확인하였다.
기존의 방법과 제안한 방법의 성능을 비교하기 위하여 동일한 신호에 대해서 실제적으로는 불가능하지만 잡음의 주파수 스펙트럼이 알고 있다고 가정한 다음, 대표적인 알고리즘인 스펙트럼 감산법에 의한 잡음제거 결과를 표 4에 제시하였다.
제안한 방법의 결과인 표 2와 이상적인 스펙트럼 감산법에 의한 결과인 표 4를 비교하여 보면, 충돌성 잡음의 경우, 이상적인 스펙트럼 감산법과 비교할 때, 제안한 방법은 대략 SNR이 3dB~7dB 이하로 잡음 억제 효과에 있어서는 이상적인 결과에 접근하고 있는 것을 확인할 수 있다.
Ⅴ. 결 론
본 연구에서는 모폴로지 특성 분석 방법을 이용하여 충돌성 잡음이 섞인 음성으로부터 잡음을 제거하는 알고리즘을 제안하였다. 모폴로지 성분 분석 시, 기저계를 변형하여 시작 시간이 다르고, 지속시간이 짧은 신호의 부분 공간을 복수개로 정의한 다음, 잡음과 음성 신호를 DFT 기저계를 이용하여 근사화하였다. 따라서 지속 시간의 차에 따라 음성을 DFT 기저로 잡음을 그 지속 시간만을 고려한 부분 공간 벡터의 합으로 표현함으로서 각각의 스파스 표현을 얻었다. 시뮬레이션을 통하여 여러 가지 잡음이 중첩된 신호에 대해서 제안한 방법을 실험하였고, 지속 시간이 짧은 잡음에 대하여 제안한 방법의 유효성을 확인하였다. 금후에는 잔향이 있는 환경에서 제안한 방법의 유효성을 확인하고, 계산 비용을 저감시키는 방법에 관하여 연구하고자 한다.
Acknowledgments
이 논문은 2016~2018학년도에 청주대학교 산업과학연구소가 지원한 학술연구조성비(특별연구과제)에 의해 연구되었음.
References
-
S. F. Boll, "Suppression of acoustic noise in speech using spectral subtraction", IEEE Trans. ASSP, 27(2), p113-120, Apr), (1979.
[https://doi.org/10.1109/tassp.1979.1163209]

-
S. Sardy, A. G. Bruce, and P. Tseng, "Block coordinate relaxation methods for nonparametric wavelet denoising", Journal of Computational Graphical Statistics, 9(2), p361-379, (2000).
[https://doi.org/10.2307/1390659]

-
P. J. Wolfe, and S. J. Godsill, "Efficient alternatives to the Ephraim and Malah suppression rule for audio signal enhancement", EURASIP Journal on Applied Signal Process-ing, 2003(10), p1043-1051, Oct), (2005.
[https://doi.org/10.1155/s1110865703304111]

- T. Choi, and S. Kim, "A Speech Segregation Technique for Speech Quality Enhancement on Noise Environment", Journal of KIIT, 10(10), p47-53, Oct), (2012.
-
S. Gazor, and W. Zhang, "Speech enhancement employing Laplacian-Gaussian mixture", IEEE Trans. on Speech and Audio Peocessing, 13(5), p896-904, Sep), (2005.
[https://doi.org/10.1109/tsa.2005.851943]

- J. I. Stark, M. Elad, and D. L. Donoho, "Image decomposition via the combination of sparse representation and a variational approach", IEEE Trans. on Image Process., 14(10), p1570-1582, Oct), (2005.
-
C. Han, and H. Y. Kim, "An Efficient Filtering Method for Dynamic Trans-aural Systems", Journal of KIIT, 13(1), p31-38, Jan), (2015.
[https://doi.org/10.14801/jkiit.2015.13.1.31]

-
S. S. Chen, D. L. Donoho, and M. A. Saunders, "Atomic Decomposition by Basis Pursuit", SIAM Journal on Scientific Computing, 20(1), p35-61, Jan), (1998.
[https://doi.org/10.1137/s1064827596304010]

-
T. Lotter, and P. Vary, "Speech enhancement by MAP spectral amplitude estimation using a Super Gaussian speech model", EURASIP Jurnal on Applied Signal Processing, 2005(7), p1110-1126, Jul), (2005.
[https://doi.org/10.1155/asp.2005.1110]

-
Y. Zhao, X. Zhao, and B. Wang, "A speech enhancement method based on sparse reconstruction of power spectral density", CEE, 40(4), p1080-1089, May), (2014.
[https://doi.org/10.1016/j.compeleceng.2013.12.007]


1996년 3월 : 동북대학교(일본), 정보과학연구과(공학박사)
1997년 ~ 현재 : 청주대학교 전자공학과 교수
관심분야 : 음향신호처리, 3차원 입체음향, 전기음향