[ Article ]

The Journal of Korean Institute of Information Technology - Vol. 16, No. 1, pp.145-153

ISSN: 1598-8619 (Print) 2093-7571 (Online)

Print publication date 31 Jan 2018

Received 11 Oct 2017 Revised 02 Jan 2018 Accepted 05 Jan 2018

DOI: https://doi.org/10.14801/jkiit.2018.16.1.145

Effect of Chessboard Image Noise on Camera Calibration

Yeon-Serk Yu^*

*Dept. of Laser & Optical Information Engineering, Cheongju University

Correspondence to: Yeon-Serk Yu Dept. of Laser & Optical Information Eng., Cheongju University, 298, Daeseong-ro, Cheongwon-gu, Chungcheongbuk-do, 373-765, Korea Tel.: +82-43-229-8501, Email: yuys@cju.ac.kr

Abstract

Camera calibration is based on the calculation of camera parameters that are based on characteristic point coordinates found by using one dimensional lines, 2 dimensional planes, or three-dimensional sequencing of a target. The accuracy of camera calibration depends on the accuracy of the characteristic point coordinate measurements. This research studied the relation between characteristic point extraction accuracy with image noise using a black and white chessboard pattern typically used as two-dimensional pattern targets. The black and white chessboard pattern, used as the reference image, was added with Gaussian noise and Speckle noise each at different intensity levels to understand how optical noise influenced characteristic point extraction, focal length error, principal point error, radial distortion coefficients, tangential distortion coefficients, mean reprojection errors and other camera calibration parameters. The results of the study indicated that Gaussian noise produced greater errors than Speckle noise having a mean reprojection error increase ratio that was approximately 1.14 times greater.

초록

카메라 보정은 기준이 되는 1차원 선분이나 2차원 평면 배열 또는 3차원 배열 표적들을 사용하여 구한 특성점 좌표들로부터 카메라 변수 들을 계산한다. 카메라 보정의 정확도는 특성점 좌표 측정의 정확도에 의존하게 된다. 본 연구에서는 2차원 배열 표적으로서 흔히 사용되는 체스보드 흑백 무늬 패턴을 사용하여 영상 잡음과 특성점 추출 정확도의 관계를 다루었다. 기준 이미지인 체스보드 흑백 무늬 패턴에 가우시안 영상 잡음과 스페클 영상잡음을 각각 다른 세기 수준으로 추가하여 광학적 잡음이 특성점 추출과 초점거리 에러, 주요점 에러, 방사 왜곡계수, 탄젠셜 왜곡계수, 평균 재투영 에러 등 카메라 보정 변수들에 미치는 영향을 실험적으로 분석하였다. 결과적으로 보면 가우시안 영상 잡음이 스페클 영상잡음 보다 더 크게 에러를 발생 시켜 평균 재투영 에러의 증가 비율이 약 1.14배 더 크게 영향을 끼침을 알 수 있었다.

Keywords:

camera calibration, Gaussian noise, Speckle noise, mean reprojection error

Ⅰ. Introduction

The results of camera calibration influence the measurement accuracies of image measurements and because of this, it is considered an important subject of machine vision and photogrammetry. The use of camera calibration makes it possible to determine intrinsic parameters that differ according to camera optical characteristics and composition as well as extrinsic parameters regarding object position, camera bearings, and reference coordinate systems [1]-[3]. Depending on the measured subject and purpose of measuring, camera calibration systems can be classified into systems requiring automation and quick measurement speeds, and systems requiring greater precision than quick measurement speeds. In most cases, precision is more important than measurement speeds and the measurement precision of typical image measurement systems depend on the precision of camera calibration. The process of camera calibration first requires an understanding of the reference coordinate system and characteristic point coordinates within an image plane. Characteristic points are found and calculated by taking photographs of a target object from multiple angles in reference to one dimensional lines, two-dimensional planar patterns, or three-dimensional patterns. After then camera parameters are calculated using such characteristic points [4][5]. Therefore the accuracy of camera calibration depends on the accuracy of characteristic point coordinates. To find the characteristic points several types of two-dimensional image patterns such as rectangular chessboard patterns, centroids of circular shapes, maximum strength points of Sin2D patterns, binary lattice structure corner points, and centroids of Gaussian point grids have been studied [6]-[8]. Also, according to the two-dimensional image pattern types, characteristic point extraction algorithms found in image phase-extraction interpretation methods [9], centroid methods to find peak locations, corner location finding methods conic fitting methods [10], and orthogonal complex moment methods have been studied [11][12]. However, due to the fact that two-dimensional target reference planes that have regular patterns are easy to produce and require less costs, methods of finding characteristic points based on four corner locations or the sides or center of two-dimensional planar image patterns are generally used [13]-[15].

Using a two-dimensional black and white chessboard patterned plate added with different intensity ratios of Gaussian noise and Speckle noise, the effects of the addition of optical noise to the reference image on characteristic point extraction, camera intrinsic parameters, and calibration were analyzed through experimentation.

Ⅱ. Camera Calibration

2.1 Camera Model

There are several methods of camera calibration. Of these methods, the goniometer method makes use of a very precise grid plate placed on the image plane of a camera and the angles responding to the grid intersection from an object are measured through the goniometer, which in turn are compared to nominal and real values to find the distortion values. In the collimator method, a collimator set-up with many defined yet different angles is used to project the test patterns on an image plane. The camera focus is set to infinity and the measured nominal values and real values are compared to find the parameters of interior orientation. Compared to such methods, a simpler and generally used method is the camera calibration model studied by Zhang [5] and Tsai [13], which applies the image forming principles of pinhole cameras. In this model, a three-dimensional object point is projection a two-dimensional image plane of the camera.

Let the three-dimensional object points as P_o = (X_o,Y_o,Z_o) in the world frame. And their projection on the two-dimensional image plane of the camera as P_c = (X_c,Y_c,Z_c) in the camera frame. Between the P_o and P_c are related to the location of the image points geometrically rotates and moves translationally. Because of this, the translational vector T and rotation matrix R can be used to represent such changes using the rigid body motion equation P_c = R +P_o +T. The relation between the image points P_c = (X_c,Y_c,Z_c) of the camera sensor plane and the object points P_o = (X_o,Y_o,Z_o), can be represented as[5][13]

x i y i = X c / Z c Y c / Z c = f Z o X o Y o

(1)

where (x_i, y_i) are the normalized coordinates of P in the image sensor frame, f is the effective focal length. However, actual cameras in use do not form images like a pinhole camera using the rectilinearly of light rays but rather forms images using a lens system, which results in the representation of lens-induced aberrations on the image. In particular, distortions between the plane- based camera image recording sensors and the image forming properties between the object and the lens, are the main reason behind changes of an entire image. Distortions are classified into radial distortions that present radial displacements of image points on the image plane and tangential distortions, a type of de-centering distortion, that results when the center of curves of lens surfaces of the lens system are not accurately on top of the same optical axis. An approximation of the coordinate system based on radial distortion can be represented as [4].

x r d y r d = 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 x i y i

(2)

where k₁, k₂, k₃ refer to the radial distortion coefficients and r² = x² + y². Tangential distortion can be represented as

x t d y t d = 2 k 4 x i y i + k 5 r i 2 + 2 x i 2 k 4 r i 2 + 2 y i 2 + 2 k 5 x i y i x i y i

(3)

where k₄ and k₅ refer to the tangential distortion coefficients. For simple use, the coordinate system of the distorted image points including both radial and tangential distortions was represented as (x_d, y_d) and in consideration that images form on camera sensor device surfaces in pixel units, the pixel coordinates [ u,v ] within the sensor surface were rewritten as

u v 1 = f u α c x 0 f v c y 001 x d y d 1

(4)

where c_x and c_y refer to the coordinates of the principle points, α refers to the aspect ratio, and a f_u and f_v refer to the focal lengths in pixel units found by dividing the lens focal length by the size of the image sensor. Thus, this model includes internal parameters such as f, α, x_o and y_o distortion coefficients k₁, k₂, k₃, k₄ and k₅ as its parameters. The goal of the camera calibration process is the determination of the optimal values of such parameters based on the known two-dimensional or three-dimensional observed target image.

2.2 Chessboard Pattern Characteristic Point Extraction and Image Noise

Chessboard patterns are composed of small black and white squares and the corner points of each square become the characteristic points. The corner points of the squares are detected using the Harris corner detection method [16].

R x, y = det M x, y - k ⋅ t r a c e 2 M x, y

(5)

where [M (x,y)] refers to local autocorrelation function related matrices and det[M ] and trace [M ] refer to the trace and determinant values of each matrix [M ], respectively. Should the R (x,y) value of a point exceeds the predetermined limit value, the point is perceived as a corner. In general, precision of the Harris detection method is at the pixel level.

Optical noise of images refers to the random distribution of light according to the frequency and intensity added to signal intensity. At this point, should the noise present within the rectangular grid-type sample, given from within the image, have a normal distribution with a zero average, such noise is considered to be Gaussian noise or white noise. In addition, speckle noise refers to a type of optical image noise that multiplies equally distributed random noise having an average value of zero that randomly changes in intensity with an optical image having an intensity distribution of I [17][18].

Ⅲ. Experiment and results

3.1 Camera Distortion Correction Measurement System

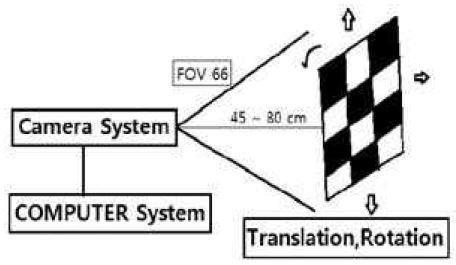
A two-dimensional chessboard pattern was used as the reference coordinate system that formed the image. The used black and white chessboard pattern was square-shaped having a side length of approximately 15.9 mm and 10 × 14 sequences were printed and used. The Microsoft HD5000, used for the experiment, had a CMOS sensor still image pixel resolution of 1280 × 800, an optical lens system having a diagonal field of view of 66^o, and a device that automatically adjusts exposure and focus. The chessboard pattern was used to capture various images at a distance of 45 cm ∼ 80 cm at various angle and slope rotations and tilts as well as left and right movements. Also, for each condition, approximately 11 ∼ 13 different angles of photos were used. Image capturing was undertaken using a computer, and Fringe Processor (Bias Co.) software and camera calibration was undertaken using the camera calibration toolbox [19] developed by Jean-Yves Bouguet at Matlab (Mathworks company). For the purpose of measuring the effects that the image noise added to the chessboard pattern target, which is the reference of the coordinate points, had on camera calibrations, several measurements of the optical images added with Gaussian noise and Speckle noise. The noise of each levels having zero average values according to noise intensity at different noise distribution changes were taken. Fig. 1 presents a schematic diagram of the measurement system.

Fig. 1.

Camera calibration measurement system

Fig. 2 presents the chessboard patterns applied with different intensity levels of Gaussian noise and Speckle noise. The added noise levels between levels of 0.001 and 0.25 were categorized into 7 levels.

Fig. 2.

Chessboard patterns added with the noise used for calibration, (a) Gaussian noise level: 0.001, (b) Speckle noise level: 0.001, (c) Gaussian noise level: 0.1, (d) Speckle noise level: 0.1

Table 1 presents the standard deviation values of each noise intensity level for each of the noises.

Table 1.

Standard deviation values of different noise intensity levels added to the chessboard pattern

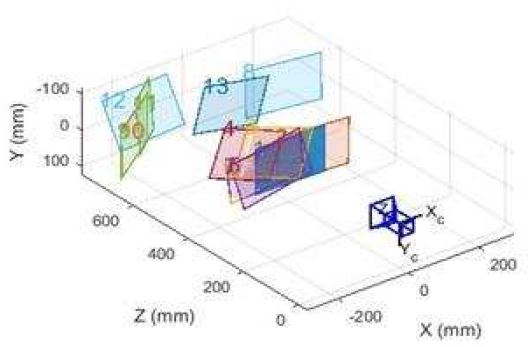
Fig. 3 presents the locations of the chessboard patterns during the camera calibration process and the camera capturing process according to different rotating angles. The camera and captured chessboard pattern locations were changed as shown in the figure. However, increased noise levels resulted in cases in which the corner points of the squares of the chess patterns were not perceived. Because of this, chessboard patterns having different locations and rotation displacements were used in the calibration.

Fig. 3.

Camera and chessboard pattern arrangement diagram to capture the image

Fig. 4 compares the standard deviation values of the Gaussian noise and speckle noise with different intensity levels and distributions as the data in Table 1. As shown in the figure, since the standard deviation of the two noise distributions is similar, the standard deviation value is used for the comparison of the experimental data.

Fig. 4.

Relationship between the noise intensity level and the standard deviation values of each of the two types of noise

Fig. 5, presents the reprojection error values within the plane of the characteristic points of the parameters found through the camera calibration process based on chessboard pattern images added with different intensity levels of two types of noises. Through this, the effects of Gaussian noise and Speckle noise on reprojection coordinates according to increases in noise intensity levels were observed.

Fig. 5.

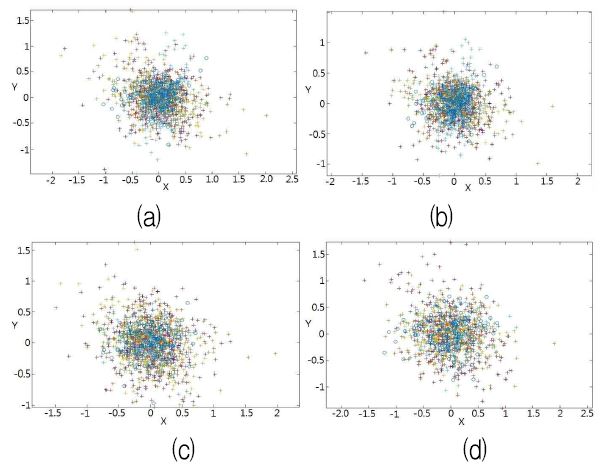
Gaussian noise and Speckle noise intensity level induced changes of reprojection error values, (a) Gaussian noise level: 0.001, (b) Speckle noise level: 0.001, (c) Gaussian noise level: 0.1, (d) Speckle noise level: 0.1

During the process of camera calibration, intrinsic parameters such as focal length, principle point, and skew as well as extrinsic parameters such as lens system-based distortion, rotation matrices, and translation vectors can be calculated. Fig. 6 presents changes in average values of focal length errors and principle point errors due to Gaussian noise and Speckle noise.

Fig. 6.

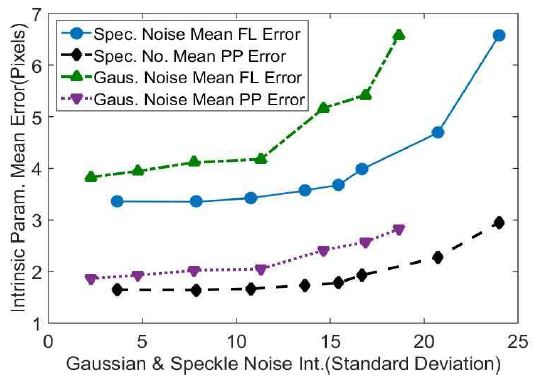
Changes in focal length error and principle point error average values (pixel units) due to Gaussian noise and Speckle noise

The standard deviation values presented in Table 1 were used as the noise intensity level values during this process. As shown in the figure, in the case of Gaussian noise, when the noise intensity standard deviation increased by 7.93 times from 2.35 to 18.65, average focal point length error increased by approximately 2.76 from 3.35 pixels to 6.57 pixels and the ratio between focal length error increases and noise increases was found to be ΔFLE/ΔNoise = 2.76/7.93 = 0.35. The average principle point error was found to increase by 1.52 times from 1.86 pixels to 2.82 pixels and the ratio between principle point error increases and noise increases was found to be ΔMPLE/ΔMNSD = 1.52/7.93 = 0.19. In the case of Speckle noise, average focal length error was found to increase by 1.96 times from 3.35 pixels to 6.57 pixels when the noise intensity level standard deviation increased by 9.8 times from 2.11 to 20.7 and the ratio between focal length error increases and noise increases was found to be ΔFLE/ΔNoise = 1.96//9.8 = 0.2. Average principle point error was found to increase by approximately 1.79 times from 1.64 pixels to 2.94 pixels and the ratio between principle point error increases and noise increases was found to be ΔMPLE/ΔMNSD = 1.79/9.8 = 0.18. When examining the results regarding error increase ratios of focal lengths based on increases in intensity of noise, it was found that Gaussian noise resulted in 0.35/0.2 = 1.75 times greater error than Speckle noise. In the case of principle point error, Gaussian noise was found to result in 0.19/0.18 = 1.05 times greater error than Speckle noise.

Through lens distortions, the radial distortion values and tangential distortion values were found. Fig. 7 presents a comparison of the changes in the 3 coefficients of radial distortion k₁, k₂ and k₃ presented in equation (2). The results indicated that coefficient k₁ was found to have almost no change regarding increases in noise intensity levels of both types of image noises. In the case of the coefficient k₂ and k₃ Gaussian noise was found to have small effects in noise intensity level standard deviation values higher than 15 whereas Speckle noise was found to have a large effect at noise intensity level standard deviation values equal to or greater than 11.

Fig. 7.

Comparison of the effects of Gaussian noise and Speckle noise on radial distortion coefficients

Fig. 8 presents a comparison of the changes in errors of the 3 coefficients of radial distortion, k₁, k₂ and k₃ , according to the two types of noises. In the case of Gaussian noise, the error of radial distortion coefficients did not present significant changes up to the noise intensity level standard deviation value of 18. However, in the case of Speckle noise, the coefficients were found to be largely affected at noise intensity level standard deviation values equal to or greater than 20.

Fig. 8.

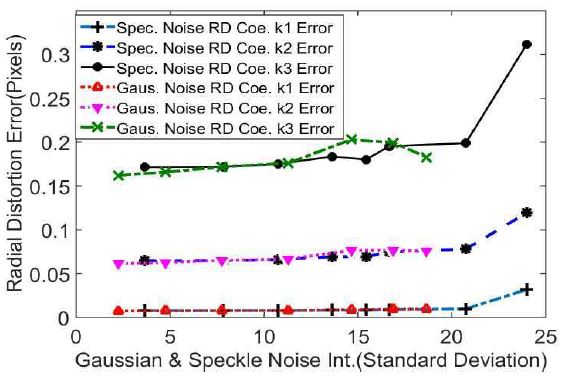
Comparison of the effects of Gaussian noise and Speckle noise on radial distortion coefficient errors

Fig. 9 and 10 presents the comparison between changes in error values and the two coefficients of tangential distortion, k₄ and k₅, presented in equation (3) according to the two types of noises. The results indicated that the values of coefficients k₄ and k₅ have a small value of 10^-3 pixels, and that k₄ has a negative value and is largely affected at noise intensity level standard deviation values of 10 and higher according to the two types of image noises. k₅ was found to be influenced at very small levels according to the different noise intensity levels of both Gaussian noise and Speckle noise. An examination of the changes in tangential distortion errors as presented in Fig. 10, indicated that the coefficient had a very small value of 10^-4 pixels yet changed according to noise increases.

Fig. 9.

Comparison of the effects of Gaussian noise and Speckle noise on tangential distortion coefficients

Fig. 10.

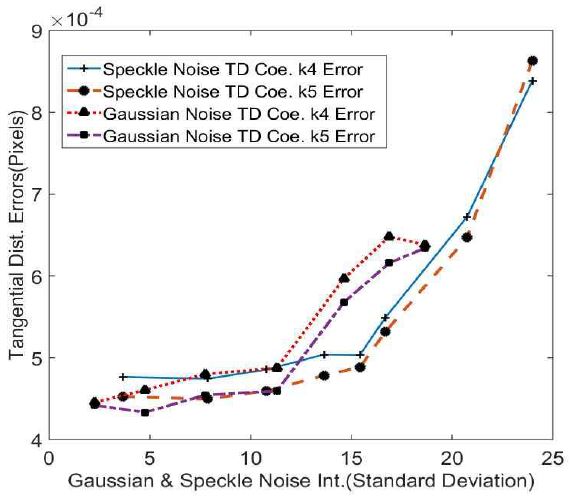
Comparison of the effects of Gaussian noise and Speckle noise on errors of tangential distortion coefficients

Fig. 11 presents the average reprojection error values found during the camera calibration process based on the addition of different intensity levels of Gaussian noise and Speckle noise to the image. The results indicated that Gaussian noise rather than Speckle noise had a greater effect under the same image noise intensity levels. In the case of Gaussian noise, mean reprojection error increased by approximately 1.31 times from 0.384 pixels to 0.504 pixels when the noise intensity level standard of deviation increased by 7.93 times from 2.35 to 18.65 and the ratio between mean reprojection error increases and noise intensity increases was found to be ΔMRPE/ΔNoise = 1.31/7.93 = 0.16.

Fig. 11.

Comparison of the effects of Gaussian noise and Speckle noise on mean reprojection error

In the case of Speckle noise, when the noise intensity level standard deviation increased by approximately 9.8 times from 2.11 to 20.7, average reprojection error was found to increase by approximately 1.42 times from 0.344 pixel to 0.49 pixel, and the ratio between mean reprojection error increases and noise intensity increases was found to be ΔMRPE/ΔNoise = 1.42/9.8 = 0.14. A comparison of the mean reprojection error increase ratios found based on increases in Gaussian and Speckle noise, indicated that Gaussian noise-induced effects were 0.16/0.14 = 1.14 times greater than Speckle noise-induced effects.

Ⅳ. Conclusion

The precision of general optical profilometry systems using the optical images, depends on the precision of calibration. Chessboard patterns are typically used as the target reference object, and the reference image captured through a camera includes optical image noise that affects corner point extraction. This study analyzed how the different types and intensities of image noises such as Gaussian noise and Speckle noise added to the target image affects camera parameters through experimentation. Quantitative optical image noise including chessboard patterns were used to undertake camera calibration, and camera intrinsic parameters such as focal length, principle point, and skew as well as extrinsic parameters such as distortion due to the lens system, rotation matrices, and translation vectors were found. The intensity levels of the optical image noises were presented through a standard deviation function and camera parameters and error values were presented in pixel units. When examining the results regarding error increase ratios of focal lengths based on increases in noise intensity, it was found that Gaussian noise resulted in 1.75 times greater error than Speckle noise. In the case of principle point error, Gaussian noise was found to result in 1.05 times greater error than Speckle noise. Through lens distortions, the radial distortion values and tangential distortion values were found. Of the three coefficients of radial distortion, k₁, k₂ and k₃, coefficient k₁ was found to have almost no change when subjected to increases in noise levels of the two types of image noises. In the case of coefficients k₂ and k₃, Gaussian noise was found to have at least small effects up to the noise intensity level standard deviation value of 18 whereas Speckle noise was found to have an effect at noise intensity level standard deviation values equal or greater to 11. An examination of the ratio between increases in noise intensity and increase of mean projection errors indicated that Gaussian noise had approximately a 1.14 times greater effect than Speckle noise.

Acknowledgments

This work is supported by Industrial Science Research of Cheongju University during School Year 2016 to 2017

References

F. Remondino, and C. Fraser, "Digital camera calibration methods: considerations and comparisons", ISPRS commission V symposium, Image Engineering and Vision Metrology, 36, p266-272, Jan), (2006.
D. C. Brown, "Close-range camera calibration", Photogrammetric Engineering, 37(8), p855-866, Aug), (1971.
J. H. Yoo, and Y. S. Yu, "A Study on precalibration techniques in fringe reflection profilometry", Journal of KITT, 11(12), p59-69, Dec), (2013. [https://doi.org/10.14801/kiitr.2013.11.12.59]
Alexander Hornberg, "Handbook of machine vision", Wiley-VCH, p333-358, Aug), (2006.
Z. Zhang, "A flexible new technique for camera calibration", IEEE Trans. on Pattern Analysis and Machine Intel., 22(11), p1330-1334, Nov), (2008. [https://doi.org/10.1109/34.888718]
X. Meng, H. Li, and Z. Hu, "A new easy camera calibration technique based on circular points", Pattern Recognition, 36(5), p1155-1164, May), (2003. [https://doi.org/10.1016/s0031-3203(02)00225-x]
Y. Liu, and X. Su, "Camera calibration with planar crossed fringe patterns", Optik-International Journal for Light and Electron Optics, 123, p171-175, (2012). [https://doi.org/10.1016/j.ijleo.2011.02.026]
L. Li, W. Zhao, F. Wu, Y. Liu, and W. Gu, "Experimental analysis and improvement on camera calibration pattern", Optical Engineering, 53(1), p0131041-0131047, Jan), (2014. [https://doi.org/10.1117/1.oe.53.1.013104]
L. Kruger, and C. Wohler, "Accurate chequer board corner localization for camera calibration", Pattern Recognition Letters, 32, p1428-1435, Apr), (2011.
B. F. Alexander, and K. Chew, "Elimination of systematic error in sub-pixel accuracy centroid estimation", Optical Engineering, 30(9), p1320-1331, Sept), (1991.
G. Xu, X. Zhang, X. Li, J. Su, and Z. Hao, "Global calibration method of a camera using the constraint of line features and 3D world points", Measurement Science Review, 16(4), p190-196, Aug), (2016. [https://doi.org/10.1515/msr-2016-0023]
S. Ghosal, and R. Mehrotra, "Orthogonal moment operators for sub-pixel edge detection", Pattern Recognition, 26(2), p295-306, Feb), (1993. [https://doi.org/10.1016/0031-3203(93)90038-x]
R. Y. Tsai, "A versatile camera calibration technique for high accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses", IEEE Journal of Robotics and Autom., 3(4), p323-344, Aug), (1987. [https://doi.org/10.1109/jra.1987.1087109]
L. Li, W. Zhao, F. Wu, and Y. Liu, "Flat mirror tilt piston measurement based on structured light reflection", Optics Express, 22(22), p27707-27716, Nov), (2014.
S. Kay, "Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter/reverberation", IEEE Journal of Selected Topics in Signal Processing, 1(1), p31-41, Jun), (2007.
C. Harris, and M. Stephens, "A combined corner and edge detector", Alvey Vision Confere., K.D. Baker Ed., 10, p147-151, Oct), (1988. [https://doi.org/10.5244/c.2.23]
M. V. Sarode, and P. Deshnukh, "Reduction of speckle noise and image enhancement of images using filtering technique", International Journal of Advancements in Technology, 2(1), p30-38, Jan), (2011.
Y. S. Yu, "A study on image noise effect to the phase error in phase shifting profilometry", Journal of KITT, 14, p45-52, Jan), (2016. [https://doi.org/10.14801/jkiit.2016.14.1.45]
Camera calibration toolbox for Matlab: http://www.vision.caltech.edu/bouguetj/calib_doc/, [Accessed: Feb. 05, 2017]

Author

Yeon-Serk Yu

1979 : BS degree in Science Ed. ChungBuk National University

1982 : MS degrees in Physics Ed., Chungbuk National University.

1988 : PhD degree in Physics in Soongsil University.

1988 ~ 2017 : University Professor, Cheongju University.

Research interests : Optical Metrology, 3-D Metrology, Optical Measurement, Optical Thin Films Design.

Noise Level	N. L. Standard Deviation Value
Noise Level	Gaussian Noise	Speckle Noise
0.001	2.35	2.11
0.01	4.75	6.74
0.025	7.75	10.69
0.05	11.30	13.58
0.075	14.64	15.36
0.1	16.89	16.63
0.25	18.65	20.70