CUDA와 OpenMP를 이용한 NEC-2 코드 속도 향상

Ⅰ. 서 론

항공기나 선박과 같은 대형 표적에 대해서 실제 RCS(Radar Cross Section) 및 EMI(Electro Magnetic Interference) / EMC(Electro Magnetic Compatibility)를 측정 하는 것은 실내 측정 환경을 구축하는데 어려움이 있으며 실외 측정의 경우에도 다중경로 문제 등으로 인해 여러 가지 문제가 있다. 하지만 컴퓨터의 발전과 전파 해석 소프트웨어의 발전으로 RCS 및 EMI/EMC를 시뮬레이션을 통해 획득하는 것이 가능하게 되었다[1].

CPU(Central Processing Unit)의 발전은 싱글코어의 클럭 속도를 높이거나 성능을 향상시키는 방향이었다. 하지만 CPU 제조의 한계에 부딪침에 따라 싱글코어에서 코어 수를 늘리는 멀티코어 방식으로 발전하였다. 기존의 순차적인 프로그램은 싱글코어로 구현되어 있어 멀티코어를 가진 하드웨어라도 순차적인 코드의 성능은 향상되지 않았다. 따라서 순차적인 코드가 멀티코어에서 병렬화로 동작시키기 위해 OpenMP(Open Muti-Processing)가 개발되었고 프로그램의 병렬화를 위한 표준이 되었다[2].

GPU(Graphics Processing Unit)는 프로세서의 연산 효율을 향상시키는 방향으로 발전하게 되었다. GPU 코어를 대량으로 증가 시키고 빠른 메모리를 채택하여 GPU와 메모리 간 데이터 전송 격차를 줄였으며 대용량 데이터를 병렬처리 하는데 좋은 해결 방안이 되었다. CUDA(Compute Unified Device Architecture)는 강력해진 GPU의 성능을 이용하여 GPGPU의 통합 개발 환경을 제공한다. GPGPU는 ‘General Purpose Graphics Processing Unit’의 약자이며, 강력해진 GPU의 성능을 그래픽 처리뿐만 아니라 일반적인 데이터 처리에도 사용하는 것을 의미한다[3]-[5].

본 논문에서는 모멘트법 기반의 전파수치해석 코드인 NEC-2를 병렬코어 기반의 OpenMP와 CUDA기반의 cuBLAS를 이용하여 병렬처리 알고리즘을 제안하였다. NEC-2는 포트란 언어를 기반으로 개발된 32bit 코드이다[6]. 32bit 코드로 개발된 NEC-2 코드는 OS(Operating System)에 의한 메모리 제한이 있어서 큰 구조물에 대하여 해석이 불가능하다. 따라서 32bit 코드를 64bit 코드로 변경하여 메모리의 제한을 해결하고 전파 해석 하는데 시간이 많이 소요되는 부분에 대하여 병렬처리 기법을 적용하여 성능을 대폭 향상 시켰다. 또한 기존의 NEC-2 코드와 개발된 코드 그리고 상용화 툴인 FEKO를 이용하여 해석 결과를 검증하고 성능 비교를 하였다.

Ⅱ. NEC-2 코드의 병렬처리 구현

2.3 NEC-2 코드의 병렬화

NEC-2 코드는 모멘트법을 이용함에 따라 모멘트 산란 행렬 계산이 필요하다. 모멘트 산란 행렬 계산부는 다소 복잡한 제어 연산이 필요함에 따라 병렬코어 기반의 OpenMP를 적용하였다. 행렬을 생성시에 OpenMP를 적용하여 성능을 향상시켰으며, 산란 행렬 생성은 원소별 독립 계산이 가능함으로써 매우 큰 와이어 메쉬에 대해서도 병렬 코어 개수에 비례하는 연산 가속화가 가능하다.

NEC-2에서 표면의 전류 분포 I를 구하기 위한 행렬 연산은 다음과 같다.

$\[ ZI=V\to I=Z^{-1}V \]$

(1)

이때 I 는 우리가 구하고자 하는 미지수인 I_m을 원소로 갖는 벡터이며 V 는 주어진 전압 벡터이다.

이 행렬 계산은 가우스 소거법을 통해서 해결되는데 기본 단계는 가우스 소거법을 조금 변형시켜 LU분해를 적용하여 행렬 Z를 식 (2)와 같이 상 삼각 행렬U와 하 삼각 행렬L의 곱으로 분해를 한다[6]-[8].

$\[ Z=\left[L\right]\left[U\right] \]$

(2)

그러면 식 (1)은 식 (3)과 같이 된다[6][8].

$\[ \left[L\right]\left[U\right]\left[I\right]=\left[V\right] \]$

(3)

행렬 I 를 구하기 위해서는 다음과 같이 두 단계로 계산된다[6][8].

$\[ \left[L\right]\left[F\right]=\left[V\right] \]$

(4)

식 (4)와 같이 전진대입법을 사용하여 [F ] 를 구한다[6][8].

$\[ \left[U\right]\left[I\right]=\left[F\right] \]$

(5)

식 (5)와 같이 역대입법을 사용하면 [I ]에 대하여 풀리게 된다[8].

표면 전류 도출을 위한 가우스 소거법은 순차적 연산이 주를 이루기 때문에 OpenMP를 이용한 병렬화는 효용성이 떨어진다. 이에 따라 고속 병렬화를 구현하기 위해 CUDA 기반의 cuBLAS를 적용하여 NEC-2 코드의 해석 속도를 개선하였다. cuBLAS는 CUDA로 가속화 된 BLAS(Basic Linear Algebra Subroutines) 기능을 제공하는 가장 보편적인 라이브러리 중 하나이다[5]. BLAS는 벡터 및 행렬 연산의 문제를 효율적으로 구하기 위한 수학적 소프트웨어 패키지이다.

CUDA 기반의 cuBLAS는 LU분해를 위한 라이브러리를 제공하며 함수명은 zgetrf()와 zgetrs()으로 구현되어 있다. zgetrf()는 행렬의 LU 인수분해를 수행하기 위하여 사용되며, zgetrs()는 전진대입법과 역대입법을 해주는 루틴이다. cuBLAS를 이용한 LU분해의 코드 구현은 표 1과 같다[9].

Table 1.

Code of LU decomposition using cuBLAS

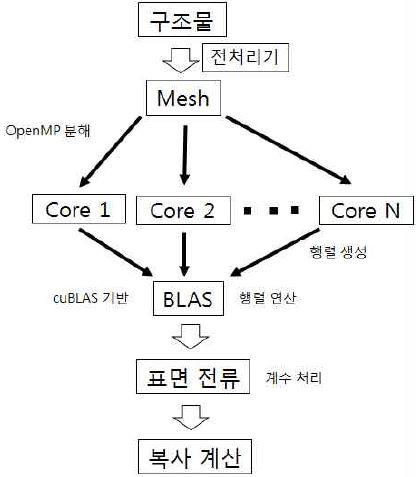
그림 1은 NEC-2 코드 병렬화 과정을 보여준다. 구조물에 대한 매쉬의 입력이 들어오면 OpenMP를 통해 코어 수만큼 분해하여 들어가고 행렬를 생성 후 표면 전류를 도출하기 위한 행렬 연산은 cuBLAS 기반의 BLAS를 통하여 계산된다.

Fig. 1.

Parallelizing for NEC-2 code

Ⅲ. 시뮬레이션 결과 및 분석

기존의 NEC-2코드와 병렬처리를 구현한 NEC-2(OpenMP+CUDA)코드 그리고 상용화 해석 툴인 FEKO를 사용하여 같은 표적에 대한 해석 결과를 검증하고 해석 시간 및 메모리 사용량 비교하였다.

3.1 실험 환경

표적에 대한 검증 및 해석 시간 측정을 위한 컴퓨터와 그래픽 카드의 구성은 표 2와 표 3과 같다.

Table 2.

Environment of simulation computer

Table 3.

Environment of graphic card

3.2 RCS 정확도 검증

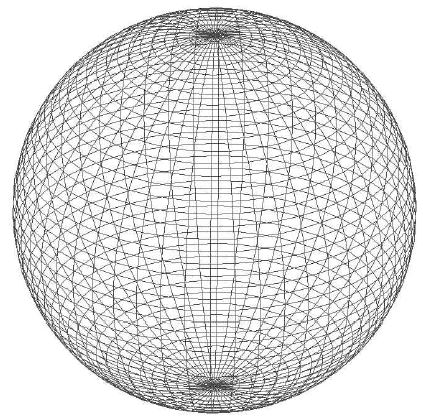
RCS에 대한 정확도 검증을 위하여 와이어 메쉬를 가지는 구를 모델링하였다[10]. 구에 대한 RCS는 정확한 이론적인 해를 구할 수 있으며, 상용화 툴인 FEKO를 이용한 구의 RCS 값은 이론적인 해와 잘 일치한다[10]. 따라서 상용화 해석 툴인 FEKO와 기존의 NEC-2코드, openMP와 CUDA 기반의 cuBLAS를 적용한 NEC-2(OpenMP+CUDA)코드를 사용하여 구에 대한 RCS를 해석하고 정확도 및 계산속도를 검증하였다[11]. 모델링한 구는 그림 2와 같다.

Fig. 2.

Sphere modeled by wire mesh

실험에 사용된 주파수는 VHF대역으로[11] 30MHz에서 300MHz까지 55포인트 간격이며, 구의 반지름은 0.5m이다. 메쉬를 나누는 기준은 300MHz를 기준으로 λ/20로 계산하였으며 와이어의 총 개수는 4950개이며, 삼각형 총 개수는 4022개이다.

Fig. 3.

RCS of the sphere wire mesh

Table 4.

Calculation time and memory usage for RCS analysis of 4950 wire mesh sphere

3.3 Far-field와 Near-field 정확도 검증

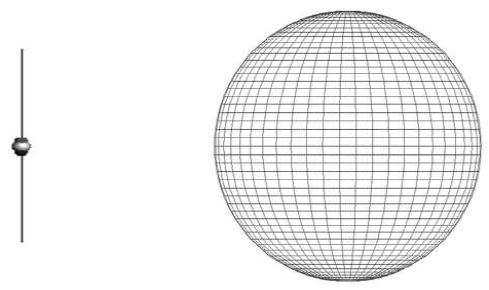
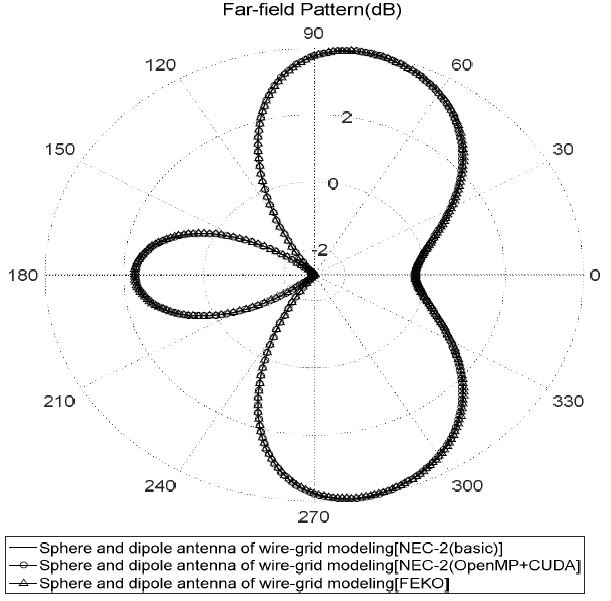
Far-field의 정확도 검증을 위하여 와이어 메쉬를 가지는 구를 모델링하고 다이폴 안테나를 와이어 메쉬로 모델링하였으며, 다이폴 안테나에 전원을 공급하고 다이폴 안테나의 방사된 전자파가 구에 미치는 영향을 확인하기 위하여 Far-field 영역에 대하여 방사 패턴을 통해 정확도를 검증하였다.

Fig. 4.

Sphere and dipole antenna modeled by wire mesh

Fig. 5.

Far-field pattern of Fig. 4

구의 반지름은 0.5m이고 구의 중심은 (0, 0, 0)이다. 다이폴 안테나 길이는 (1.2, 0, - 0.375)에서 (1.2, 0, 0.375)까지 0.75m이며, 반지름 0.0001m이다.

Near-field는 다이폴 안테나에 전원을 공급하고 방사되는 전자파가 구로부터 산란되는 결과를 통해 검증하였으며, 구의 중심(0, 0, 0)을 기준으로 구 좌표계를 사용하여 r=0.6m, θ = 90˚ , ϕ = 0 ∼ 360˚로 1˚ 간격으로 측정하였다. 측정 위치는 그림 6과 같다.

Fig. 6.

Near-field measurement point

Fig. 7.

Near-field pattern of Fig, 6 when the distance is 0.1m from sphere surface

Table 5.

Calculation time and memory usage of Far-field and Near-Field cases

Ⅳ. 결 론

본 논문에서는 대용량 행렬 연산이 필요한 모멘트법 기반의 기존의 NEC-2코드에 OpenMP와 CUDA 기반의 cuBLAS를 프로그래밍 하여 성능을 향상시켰다. NEC-2 코드는 모멘트법을 이용함에 따라 모멘트 산란 행렬 계산이 필요하다. 모멘트 산란 행렬 계산부는 다소 복잡한 제어 연산이 필요함에 따라 병렬코어 기반의 OpenMP를 적용하였으며, 또한 NEC-2코드의 행렬 연산은 가우스 소거법을 통해 계산되는데, 가장 많은 시간이 걸리는 부분이다. 시간이 많이 걸리는 행렬 연산의 가우스 소거법을 고속 병렬화가 가능하도록 하는 CUDA기반의 cuBLAS를 구현하여 성능을 향상시켰다. 성능 향상이 된 NEC-2(OpenMP+CUDA) 코드는 상용화 툴인 FEKO와 RCS/Far-field/Near-Field의 계산 결과를 비교하였을 때, 매우 잘 일치하는 것을 확인 하였다. 또한 NEC-2(OpenMP+CUDA) 코드는 NEC-2코드 보다 약 12배, FEKO보다 몇배 이상 해석 속도가 향상이 되었다.

다양한 해석 기법에도 병렬처리기법을 적용하면 성능이 향상 할 것으로 예상됨에 따라 추가적인 연구가 진행되어야 한다.

Acknowledgments

본 연구는 국방과학연구소의 지원(계약번호:UD170002DD)을 받아 수행하였으며, 이에 감사드립니다.

References

• S. W. Oh, "The Performance Analysis of Wire Grid and RWG Model in MoM", Postech Master’s Thesis, (2003).
• R. Chandra, "Parallel programming in OpenMP", Morgan kaufmann, (2001).
• Kirk, David B., and Wen-mei W. Hwu, "Programming Massively Parallel Processors: A Hands-on Approach", Morgan Kaufmann Publishers, (2010).
• Y. K. Ko, "Designing and Implementing parallel processing software for high-speed calculating process based on CUDA", Chungnam National University Master’s Thesis, (2013).
• Y. H. Jung, "CUDA parallel programming – NVIDIA parallel computing architecture CUDA using high performance GPGPU", FREELEC, (2011).
• G. J. Burke, and A. J. Poggio, "Numerical Electromagnetics Code (NEC) Method of Moments Part II: Program Description-Code", Lawrence Livermore Laboratory, Jan), (1981.
• E. Lezar, and D. B. Davidson, "GPU-based LU decomposition for large method of moments problems", Electronics letters, 46(17), p1194-1196, Sep), (2010. [https://doi.org/10.1049/el.2010.1680]
• Gibson, Walton C., "The method of moments in electromagnetics", CRC press, (2014). [https://doi.org/10.1201/9781420061468]
• NVIDIA, Cublas library – User Guide, NVIDIA Corporation, (2017).
• J. S. Jung, H. J. Kwon, and I. S. Choi, "A Study on the Analysis of Sphere RCS Using Time – Frequency Analysis", Journal of KIIT, 15(4), p89-94, Apr), (2017. [https://doi.org/10.14801/jkiit.2017.15.4.89]
• S. H. Im, S. J. Lee, and I. S. Choi, "A Study on Calculation and Comparison for VHF, UHF, L-Band RCS", Journal of KIIT, 14(5), p59-66, May), (2016. [https://doi.org/10.14801/jkiit.2016.14.5.59]