페이딩 환경에서의 딥러닝 기반 고성능 자동 변조분류 기법
초록
본 논문에서는 무선 통신 시스템에서 변조 방식을 딥러닝을 이용하여 자동으로 분류하는 방법을 제안하였다. 기존의 자동변조분류 기법들이 대부분 가우시안 채널에 대해서 설계되어 있는 반면 이러한 기법들은 페이딩 환경에서 잘 동작하지 않는 경향이 있다. 본 논문에서 제안하는 기법은 데이터로부터 먼저 다양한 종류의 통계적 특징값을 추출하고 이를 입력 데이터로 하여 완전 연결 계층으로 이루어진 딥뉴럴네트워크를 사용하여 디지털 변조 신호를 분류한다. 페이딩 채널에서의 제안하는 자동변조분류 기법을 적용하기 위해 페이딩 환경을 고려하여 훈련 데이터를 생성하였고 이를 이용하여 딥뉴럴네트워크를 훈련하였다. 제안하는 기법을 BPSK, QPSK, 8-PSK, 16-QAM, 64-QAM의 다섯 가지 종류의 변조 분류에 적용해 본 결과 페이딩 환경에서 기존의 방법에 비해 분류 정확도 측면에서 더 우월한 결과를 얻을 수 있었다.
Abstract
In this paper, we propose a deep learning-based method for automatically classifying modulation formats in wireless communication systems. While existing automatic modulation schemes are mostly designed for Gaussian channels, these techniques tend not to work well in fading environments. The proposed method extracts various kinds of statistical feature values from the data and classifies the modulation class using the deep neural network consisting of fully connected layers. In order to apply the proposed automatic modulation classification scheme in the fading channel, the training data is generated considering the fading environment and the deep neural network is trained by using it. As a result of applying the proposed method to the five kinds of modulation classifications of BPSK, QPSK, 8-PSK, 16-QAM and 64-QAM, we obtained better results in terms of classification accuracy than the existing methods in the fading environment.
Keywords:
automatic modulation classification, blind modulation recognition, deep neural network, fading channelⅠ. 서 론
무선 통신에서 디지털 신호에 대한 자동 변조 인식 기술은 시스템에 대한 사전 정보 없이 수신 신호의 변조 방식을 예측하는 것이다[1]-[4]. 보통 일반적인 디지털 통신 시스템에서는 송신 신호에 대한 변조 방식을 수신부에서 알고 있다고 가정하지만 가령 군용 통신에서 상대방의 통신정보를 분석하는 경우나 셀룰러 통신 환경에서 인접 셀의 신호를 제거해야 하는 경우에는 수신신호만을 이용하여 변조방식을 암묵적으로 분류하는 자동 변조 분류기술이 필요하게 된다.
변조 방식 인식을 위한 기존의 기술은 크게 두 가지 방법으로 분류할 수 있다. 첫 번째 방법은 수신신호의 통계적 모델을 기초로 우도함수(Likelihood Function)를 최대화 하는 방향으로 변조 방식을 분류하는 것이다. 이 방법은 변조 분류를 통계적으로 최소의 검출 오류 확률을 갖도록 설계할 수 있다. 하지만 실제 환경에서 생기는 오차나 채널의 특성에서 변화가 있는 경우 모델의 오차가 발생하여 좋지 않은 성능을 얻게 되는 단점이 있다. 그리고 다양한 종류의 상황에 대한 모델을 가정하게 되면, 알고리즘의 계산이 매우 복잡해지고 계산양도 많아지게 된다. 두 번째 방법은 기계학습 기법을 사용하는 방법이다. 이 방법은 훈련데이터를 이용해 기계학습 모델이 변조방식을 분류할 수 있도록 훈련을 시키는 방법이다. 이러한 방법은 훈련데이터가 실제 데이터의 비슷한 분포를 갖는다고 가정하면 다양한 환경에서 잘 동작할 수 있으며 계산량도 첫 번째 방법에 비해 낮은 편이다. 따라서 본 논문에서는 기계학습에 기반한 자동변조분류 방법을 다루고자 한다.
기계학습에 기반한 자동변조분류 방법은 두 가지 단계를 거치는 데 먼저 수신신호로부터 변조방식의 특성을 나타내는 특징값을 추출하는 특징값 추출단계가 있고 추출된 특징값을 이용해 변조방식을 분류하는 분류단계로 나뉘게 된다. 기존의 자동변조분류 기술에서 자주 사용하는 특징값으로는 고차통계값인 큐뮬런트(Cumulant), 신호의 크기, 주파수, 위상의 분산, 웨이블릿 계수 등이 사용된다[5]-[8]. 한편 기존에 사용되는 분류기로는 검출 트리 기법[5][7][9]이 SVM(Support Vector Machine)을 이용한 방법들[8][10][11] 그리고 ANN(Artificial Neural Network)[12][13] 등이 있다. 기존에 제안된 자동변조분류 기법은 대부분 AWGN(Additive White Gaussian Noise) 환경에 대해서 설계가 되었기 때문에 채널이 시간에 따라서 변화하는 페이딩 채널에서는 잘 동작하지 않게 된다. 현재까지 이러한 페이딩 채널을 고려하여 설계된 자동변조분류 기법은 많지 않다.
본 논문에서는 수신신호로부터 다양한 종류의 통계적 특징값을 추출하고 이를 DNN(Deep Neural Network) 구조의 분류기의 입력으로 사용하여 변조방식을 분류하는 기법을 제안한다. DNN은 다양한 데이터부터 복잡한 구조를 학습할 수 있는 능력이 있어 최근 다양한 기계학습문제에 대해 좋은 성능을 보여주었다[14]. 특히 데이터 혹은 특징값의 차수가 높은 경우에도 기존의 방법과 달리 좋은 성능을 얻을 수 있어 영상 데이터와 같이 차수가 높은 입력에 대해서도 좋은 결과를 낼 수 있다. 이러한 DNN의 특성을 활용하기 위해 제안한 기법에서는 수신 데이터로부터 다양한 종류의 통계적 특징값들을 추출하고 이를 DNN 분류기의 입력으로 사용하였다. 먼저 정보이론적 기준을 사용하여 페이딩 채널 환경에서 다양한 통계값에 대한 상관도를 분석하였다. 그 결과 레일리 페이딩 환경에서 좋은 특성을 갖는 특징값은 가우시안 채널에서의 경우와 다른 것을 확인하였다. 해당 페이딩 환경에서 자동변조분류를 수행하기 위해서 페이딩 채널에 대한 수신신호 생성하고 이를 훈련신호로 사용하여 4개의 완전 연결 계층으로 이루어진 DNN을 훈련하였다. 이를 통하여 성능을 측정한 결과 기존의 방법에 비해 매우 높은 분류 정확도를 보이는 것을 확인할 수 있었다.
Ⅱ. 제안한 기법의 특징값 추출
본 장에서는 제안한 기법에 사용하는 특징값을 소개한다. 먼저 기존에 사용했던 다양한 특징값들과 함께 새로 정의한 특징값들을 포함하여 28개의 특징값을 고려하였다. 기존 방식에서는 6~8개의 특징값을 이용해 자동 변조방식 분류에 적용하였지만, 제안한 방법에서는 DNN의 장점을 이용하기 위해 다양한 종류의 28개 특징값을 추출하였다. 이러한 특징값 계산 방법을 제시하기 위해 필요한 변수는 다음과 같다. 먼저 식 (1)에서 rI[i]는 베이스밴드 수신신호 샘플의 실수 부분의 값, rQ[i]는 허수 부분의 값을 나타내며 r[i]는 i번째 베이스밴드 신호샘플을 나타낸다.
| (1) |
이러한 베이스밴드 신호 샘플로부터 얻을 수 있는 값들을 정의하면 다음과 같다.
| (2) |
| (3) |
| (4) |
여기서 와 같이 정의되고 N은 특징값 계산에 사용된 신호의 샘플 수를 나타낸다. 한편, 식 (5)와 식 (6)에서의 ψ[i] 는 신호의 샘플 r[i] 의 위상을 나타낸다.
| (5) |
| (6) |
랜덤 변수의 큐뮬런트 통계값은 다음과 같이 정의된다.
| (7) |
π는 {1,...,n}에서 어떤 부분집합들을 잘 정하여, 처음의 집합의 각 원소가 한 부분 집합에 속하고, 그 외의 부분집합에는 속하지 않도록 하는 모든 집합의 분할을 의미한다[15]. 한편, Joint 고차 모멘트의 정의는 다음과 같다.
| (8) |
마지막으로 식 (9)에서 fc(i)는 기존 주파수 값에서 주파수의 평균값을 뺴준 값을 나타낸다.
| (9) |
위에서 정의된 변수를 통해서 먼저 설명할 12개의 특징값을 표현하면 다음과 같다.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
식 (14)는 신호의 크기의 절대값의 표준편차이고 (15)는 혼합차수 모멘트의 비를 나타낸다. (16)과 (17)은 신호의 크기의 첨도(Kurtosis)와 비대칭도 (Skewness)를 나타내고 식 (18), 식 (19)은 피크값 대비 평균값과 피크 파워값 대비 평균 파워비이다. 식 (20)은 신호의 표준화 된 값의 절대값의 표준편차이고 식 (21)에서 fN(i)은 식 (9)의 fc(i)를 심볼률로 나누어서 정규화를 시킨 주파수 값이다. 위의 12개 특징값 외에 나머지 16가지의 특징값은 고차 통계값인 큐뮬런트 특징값이다. Cnm은 Cnm = cum(x,..., x, x*, ..., x*)로 정의되는데, 여기서 x는 n-m번 사용되고 x*는 m번 사용된다[15].
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
| (35) |
| (36) |
| (37) |
제안한 기법에서는 위에서 살펴본 28개의 통계적 특징값을 변조분류에 사용하였다.
Ⅲ. 상호정보를 이용한 특징값 분석
본 장에서는 앞 장에서 살펴본 28가지의 특징값의 페이딩 환경에서의 특성을 정보이론적인 기준을 이용하여 분석하고자 한다. 또한 분류기의 연산량을 줄이기 위하여 신뢰성이 높은 특징값을 선택하는 기법도 제시하고자 한다.
먼저 변조 분류를 위한 특징값의 공헌도를 평가하기 위해서 주어진 채널 환경에서 특징값과 분류하고자 하는 변조방법 정보간의 상호 정보값을 비교해 볼 수 있다. 송신기에서 사용된 변조 방식 정보를 이산확률변수 c로 나타내면 i번째 특징값과 모듈 c에 대한 상호 정보값은 다음과 같이 정의된다[16].
| (38) |
이때, P(xi,c)는 xi와 c의 공통확률분포를 의미한다. 높은 상호 정보값은 해당 특징값이 c라는 모듈에 대한 정보를 많이 담고 있으므로 변조분류를 하는 데 더 유용하게 사용될 수 있다. 실제로 P(xi,c)의 확률밀도함수를 정확하게 알지 못하기 때문에, 다양한 변조분류 방법에 대한 특징값 샘플들을 생성한 후 두 변수간의 공통확률분포를 Parzen 윈도우 방법을 통해서 추정한다.
본 논문에서는 AWGN환경에서 SNR이 5dB인 경우 1과 레일리 페이딩 환경에서 SNR이 5dB이고 도플러 주파수를 50Hz로 설정한 경우 2와 같은 레일리 페이딩 채널에 SNR이 5dB이고 도플러 주파수가 100Hz인 경우 3을 고려하였다. 표 1에서는 가우시안 채널과 레일리 페이딩 채널에서도 28개의 통계적 특징값을 상호정보가 큰 순으로 제시하였다. 표에서 보는 바와 같이 가우시안 채널에서 좋은 특징 값과 페이딩 채널에서 강한 특징값이 차이가 나는 것을 확인할 수 있다. 페이딩 환경에서는 채널의 이득값이 시간에 따라 변하기 때문에 변조 방법에 대한 상관도가 가우시안 채널에 비해 상대적으로 떨어지는 특징값도 있었다.
한편, 위의 28개의 특징값으로부터 L개의 최적의 특징값을 선택할 경우도 있다. 예를 들면 28개의 모든 특징값을 쓰기에는 요구되는 연산량이 높은 경우에는 변조분류 성능에 가장 공헌이 큰 특징값을 선택해주어야 한다. 위의 상호 정보가 큰 L개의 특징값을 선택할 수도 있으나 이런 경우 특징값간의 상관도를 고려하지 않기 때문에 불필요하게 중복된 정보를 가진 특징값을 선택할 수 가 있다. 최적의 선택은 모든 L개의 특징값 조합에 대해 상호정보를 비교하여 최적의 특징값 그룹을 찾는 것이 되겠지만 이는 많은 계산량이 따르기 때문에 실제로 수행이 어렵다. 따라서 변조 방식과의 상관도가 크면서도 이미 뽑힌 특징값과 상관도가 낮은 특징값을 찾을 수 있도록 하는 목적함수가 [16]에서 사용되었다. 이는 다음과 같이 표현된다.
| (39) |
여기서 I(xj;c)는 해당 특징값과 해당 모듈사이의 상호 정보값을 의미한다. 그리고 Sm은 m번 수행까지 선택된 특징값들의 집합을 나타내고, X ={xi,i = 1,2,3,...28}는 28개의 모든 특징값 집합을 나타낸다. 위 식에서 첫 번째 항은 모듈과 하나의 특징값 사이의 상관도를 나타내는 항이고, 두 번째 항은 특징값끼리의 상관도를 나타낸다. 따라서 두 번 째 항을 빼는 것은 중복되는 특징값을 선택하지 않기 위해서이다. 즉, 이 전체 과정은 특정 모듈에 대하여 가장 관련성이 높은 특징값을 선택하면서 동시에 다른 특징값과 기능면에서 중복을 피하는 방식이다. 본 연구에서는 위의 목적함수를 최대로 하는 특징값을 차례로 하나씩 선택하여 L개의 특징값을 찾는 탐욕적 검색 방법(Greedy Forward Search)을 사용하였다.
표 2는 위의 검색 방법을 적용하여 차례로 선택된 특징값을 나열하고 있다. 즉, 주어진 L값에 대하여 앞에 있는 특징값부터 L개의 특징값을 선택하면 된다. 표에서 보는 바와 같이 위의 목적함수를 적용하는 경우 상호정보 순으로 나열한 특징값 순서와 다른 순으로 특징값이 선택되는 것을 알 수 있다.
Ⅳ. 자동 변조분류를 위한 DNN 구조
그림 1은 제안한 방법의 구조를 나타낸다. 먼저 수신안테나를 통하여 수신신호를 취득한 후 정합필터를 이용하여 베이스밴드 샘플을 얻는다. 2,000개의 심볼을 포함하는 구간의 신호샘플을 얻어 이를 평균이 0, 분산이 1이 되도록 정규화한 후에 이를 L개의 특징값으로 변환하게 된다. 특징값들을 각각 정규화하고 이를 DNN 분류기에 입력하여 변조 분류 결과를 출력으로 얻게 된다.
4.1 DNN 구조
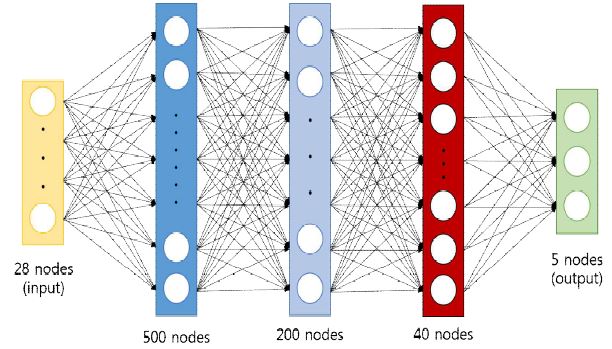
본 논문에서 제안한 DNN구조는 전체적으로 그림 2와 같으며 기본적인 완전 연결 계층 구조가 사용되었다. 입력 데이터가 들어가기 전에 앞서 설명된 전처리 과정과 특징값 선택 과정이 이루어진다. 그림 2는 제안한 방법에서 사용한 DNN의 구조를 보여준다.
28가지 전체 또는 선택된 수의 특성 값이 들어가는 입력 층을 시작으로 4개의 층으로 구성된다. 첫 번째 층은 500개의 노드 수로 이루어지며, 두 번째 층은 200개, 세 번째 층은 40개 그리고 마지막 층은 5개의 디지털 변조신호를 구분하므로 5개의 노드로 이루어져있다[14].
이 DNN구조에서 각각의 층에서는 활성함수로서, 표 3에 표현된 ReLU(Rectified Linear Unit)를 사용하였고, 마지막 층인 출력 단에서의 활성함수는 Sotfmax를 이용하였다. Softmax를 이용하게 되면 출력 값을 확률로 받아볼 수 있어 각 분류된 신호의 정확도가 어느 정도인지 알 수 있다.
4.2 DNN 트레이닝
DNN에서는 다수의 네트워크의 계수들을 훈련 데이터를 통해 업데이트 하는 트레이닝 과정이 필요하다. 트레이닝 과정의 최종적인 목적은 비용함수를 최소로 하는 DNN의 가중치 계수들을 찾는 것이다. DNN의 효과적인 훈련을 위해서는 목적에 맞는 비용함수를 정해야 한다. 제안한 방법에서는 음의 로그 우도(Negative Log-likelihood)를 비용함수로 사용하였다.
| (40) |
DNN의 목적함수는 복잡한 비선형 함수이므로 최적의 가중치 계수를 한 번의 계산으로는 알아내기 힘들다. 그러므로 계수를 기울기하강(Gradient Descent) 방식에 기반하는 역전달 기법(Back Propagation Algorithm)을 사용하였다[17]. 제안한 방법에서는 오버슈팅을 막으면서 트레이닝 시간을 절약하기 위해 몇 개의 학습율(Learning Rate)을 테스트를 했고, 그 결과로 0.001로 정하였다. 그리고 유효성 에러가 더 이상 감소하지 않으면 학습율을 반씩 줄여가는 방법을 이용하였다. 계수를 갱신할 때 미니 배치(Mini-batch) 사이즈는 50으로 하였다. 트레이닝에 사용된 피쳐벡터들 중 20%는 유효성 검사에 사용하였다. 성능 평가는 테스트를 위한 특징값 벡터를 생성하여 변조 분류 에러율을 계산하였다.
Ⅴ. 시뮬레이션 결과
5.1 시뮬레이션 결과 소개
컴퓨터 시뮬레이션을 통해서 제안한 알고리즘의 성능을 평가하였다. 우선 시뮬레이션에서 제안하는 방법을 사용해 BPSK, QPSK, 8PSK, 16QAM, 64QAM의 5개의 모듈을 분류하였다. 이를 위해 수신기에서는 롤-오프율(Roll-off Factor)가 0.2인 Root raised cosine 필터를 이용하였고 심볼률은 10 ksym/sec으로 하였다. 한 심볼당 샘플 수인 오버 샘플링 비율을 10으로 하였다. 하나의 특징값 벡터를 얻기 위해 총 2,000개의 심볼(즉 20,000개의 수신 샘플)을 이용하였다. 이러한 수신샘플을 이용하여 28개의 통계적 특징값을 계산하였다. 제안한 방법에서는 28개의 특징값을 모두 사용한 방법(제안한 방법 1)과 위에서 언급한 특징값 선택 방법을 적용하여 선택된 14개의 특징값만을 사용하는 방법(제안한 방법 2)을 사용하였다. 트레이닝을 위해 총 30,000 개의 특징값 벡터를 사용하였고 이 중 6,000개의 특징값 벡터는 유효성 검사를 위해 사용되었다. 제안한 방법의 성능 평가는 10,000개의 (각 변조방식 마다 2,000개의) 특징값 벡터를 생성하여 변조분류 정확도를 위한 테스트에 사용되었다.
제안한 방법의 성능을 몇 가지 대조군 방법과 비교하였다. 대조군으로는 기존에 제안된 ANN 분류기를 사용하는 두 방법 ANN1[12], ANN2[13]과 SVM 사용하는 방법[10]을 선택하였다.
먼저, 첫 번째 실험 결과는 AWGN환경에서 이루어졌는데, 제안한 방법 1, 제안한 방법 2, ANN1, ANN2, SVM에서 모두 완벽하게 변조방식을 분류하였다.
표 4는 레일리 페이딩 채널에서 SNR은 5dB 환경에서의 제안한 방법 변조분류 정확도를 나타낸다. 도플러 주파수는 50Hz로 설정하였다. 이때 제안한 방법 2에서는 β, C20, C40, C41, C60, C61, C62, C10,2, σap, σaa, v20, PA, K, σaf의 14개의 특징값이 선택되었다.

Results based on various structures in rayleigh fading channel with SNR = 5dB, doppler frequency = 50Hz(scale : %)
표 4에서 보는 바와 같이 제안한 방법이 기존의 방법보다 월등히 좋은 분류 성능을 나타내는 것을 확인할 수 있었다. 또한 제안한 방법 2가 제안한 방법 1에 가까운 성능을 달성하는 것을 확인할 수 있다. 제안한 방법 1이 더 좋은 성능을 나타내는 것은 DNN이 높은 차수의 특징값 벡터로부터 변조 분류를 잘 수행할 수 있는 능력이 있다는 것을 나타낸다.
표 5에서는 같은 환경에서 도플러 주파수가 100Hz 일 때의 실험 결과를 제시하고 있다. 이 환경에서 제안한 방법 2에서는 도플러 주파수가 50Hz일 때와 비슷한 β, C20, C40, C41, C42, C61, C62, C10,2, σap, σaa, v20, K, PA, σaf의 14개의 특징값이 선택되었다. 표에서는 도플러 주파수가 높아지면서 전체적으로 변조분류 성능이 저하되는 것을 확인할 수 있지만 제안한 방법이 기존의 방법에 비해 높은 성능 이득을 유지하는 것을 확인할 수 있었다.
Ⅵ. 결 론
본 논문에서는 DNN에 기반한 고성능 디지털 신호의 자동 변조 인식 기법을 제안하였다. 기존의 제시된 특성 값들과 분류하는데 있어 좋은 특성 값들을 새로 제시하여 총 28가지의 특성 값을 입력 데이터로 사용하였다. 정보이론적인 접근을 통하여 페이딩 채널 환경에서의 특징값의 특성과 성능을 분석하였고 페이딩 환경에서 변조분류에 효과적인 특징값을 선택하였다. 이러한 다양한 특징값을 입력으로 하여 DNN 분류기를 사용하여 변조방식을 분류하였다. 시뮬레이션을 통하여 페이딩 채널 환경에서 제안하는 기법이 기존의 방법에 비해 월등히 좋은 분류성능을 나타내는 것을 확인하였다.
Acknowledgments
이 연구는 방위사업청 및 국방과학연구소의 재원에 의해 설립된 신호정보 특화연구센터 사업의 지원을 받아 수행되었음.
References
- Z. Zhu, and A. K. Nandi, "Automatic modulation classification: principles, algorithms and applications", 1st ed., UK, John Wiley & Sons, (2015).
-
O. A. Dobre, A. Abdi, Y. Bar-Ness, and W. Su, "Blind modulation classification: A concept whose time has come", in Proc. IEEE/Sarnoff Symposium on Advances in Wired and Wireless Communication, Princeton, NJ, USA, 18-19, p223-228, Apr. 2005.
[https://doi.org/10.1109/sarnof.2005.1426550]

- A. M. Hazza, S. Alshebeili, and A. Fahad, "An overview of feature-based methods for digital modulation classification", in Proceedings of the 1st International Conference on Communications Siganl Processing and Their Applications, Sharjah, UAE, 12-14, p1-6, Feb. 2013.
-
E. Azzouz, and A. K. Nandi, "Automatic Modulation Recognition of Communication Signals", Springer & Business Media, New York, NJ, USA, (2013).
[https://doi.org/10.1007/978-1-4757-2469-1]

-
O. A. Dobre, A. Abdi, Y. Bar-Ness, and W. Su, "The classification of joint analog and digital modulations", Military Commun. Conf. 2005. MILCOM 2005. IEEE, p3010-3015, Oct. 2005.
[https://doi.org/10.1109/milcom.2005.1606121]

- N. An, B. Li, and M. Huang, "Modulation classification of higher order MQAM signals using mixed-order moments and Fisher criterion", in Proc. of 2nd IEEE International Conference on Computer and Automation Engineering 2010 (ICCCA 2010), Singapore, p150-153, Feb. 2010.
-
F. Q. Huang, Z. M. Zhong, Y. T. Xu, and G. C. Ren, "Modulation recognition of symbol shaped digital signals", in Proc. ICCCAS, Fujian, p328-332, May 2008.
[https://doi.org/10.1109/icccas.2008.4657787]

- X. Xin, W. Ying, and Y. Bin, "Signal classification method based on support vector machine and high-order cumulants", Wireless Sensor Network, 2(1), p48-52, Jan), (2010.
-
A. Swami, and B. M. Sadler, "Hierarchical digital modulation classification using cumulants", IEEE Trans. Commun, 48(3), p416-429, Mar), (2000.
[https://doi.org/10.1109/26.837045]

-
P. Li, Z. Zhang, X. Wang, N. Xu, and Y. Xu, "Modulation recognition of communication signals based on high order cumulants and suppport vector machine", J. China Univ. Posts Telecommun., 19, p61-65, Jun), (2012.
[https://doi.org/10.1016/s1005-8885(11)60468-8]

- G. Han, J. Li, and D. Lu, "Study of modulation recognition based on HOCs and SVM", in Proc. VTC, 2, p898-902, May), (2004.
- J. J. Popoola, and R. V. Olst, "Automatic recognition of analog modulated signals using artificial neural networks", JCTA, 2(1), p29-35, Jan), (2011.
-
J. J. Popoola, and R. V. Olst, "Effect of training algorithms on performance of a developed automatic modulation classification using artificial neural network", AFRICON, 2013. IEEE, p1-6, Sep), (2013.
[https://doi.org/10.1109/afrcon.2013.6757676]

- Y. LeCun, Y. Bengio, and G. Hinton, "Deep learning", Nature, 521, p436-444, May), (2015.
-
V. Orlic, and M. Dukie, "Automatic modulation classification: Sixth-order cumulant features as a solution for real-world challenges", 20th Telecommunication forum TELFOR, Nov), (2012.
[https://doi.org/10.1109/telfor.2012.6419230]

- H. Peng, F. Long, and C. Ding, "Feature election based on mutual information: criteria of maxdependency, max-relevance, and min-redundancy", IEEE Trans. Pattern Anal. and Machine Intel., 27(8), p1226-1238, Aug), (2006.
- D. E. Rumelhart, and G. E. Hinton, "Learning Internal Representations by error propagation", in Parallel Distributed Processing, ch. 8, MIT Press, Cambridge, MA, p318-362, (1986).

2017년 2월 : 한양대학교 전기공학과(공학사)
2017 3월 ~ 현재 : 한양대학교 전기공학과(공학석사)
관심분야 : 신호처리, 딥러닝

2016년 2월 : 한양대학교 전기공학과(공학사)
2016년 3월 ~ 현재 : 한양대학교 전기공학과(공학석사)
관심분야 : 신호처리, 딥러닝

2016년 2월 : 한양대학교 전기공학과(공학사)
2016년 3월 ~ 현재 : 한양대학교 전기공학과(공학석사)
관심분야 : 신호처리, 딥러닝

1989년 2월 : 한양대학교 전자통신공학과(공학사)
1992년 2월 : 한양대학교 전자통신공학과(공학석사)
1995년 8월 : 한양대학교 전자통신공학과(공학박사)
2004년 3월 ~ 현재 : 한양대학교 융합전자공학부 교수
관심분야 : 무선통신, 위성 및 우주통신, 신호정보

2000년 2월 : 서울대학교 전기공학부(공학사)
2002년 2월 : 서울대학교 전기및컴퓨터공학부(공학석사)
2010년 8월 : 어바나샴페인 일리노이 주립대 전기 및 컴퓨터공학부(공학박사)
2010년 8월 ~ 2013년 8월 : 시니어 엔지니어, 퀄컴 (샌디에고)
2013년 9월 ~ 현재 : 한양대학교 전기생체공학부 조교수
관심분야 : 머신러닝, 압축센싱, 통계신호처리, 자율주행