Asymptotic BER Performance Comparison of MRC and SC Diversity Techniques with Binary Signaling over Rayleigh Fading Channels

Ⅰ. Introduction

Various diversity combining techniques, such as Maximal Ratio Combining(MRC), Equal-Gain Combining(EGC), Selection Combining(SC), Switch-and-Stay Combining(SSC), etc., have been widely employed in wireless communications to exploit space diversity offered by multi-branch antenna elements and thus to effectively combat the detrimental effects of fading channels[1]-[4]. Among the several diversity combining techniques, the most popular diversity techniques are MRC and SC. In particular, MRC is known to be the optimum combining scheme and to provide the best performance, but it requires high complexity due to the Channel State Information(CSI) estimation for all diversity branches[1]. Meanwhile, SC is a simple diversity technique where the signal from the branch with the highest Signal-to-Noise Ratio(SNR) is selected[2]. Thus, the performance evaluations of MRC and SC diversity techniques have been extensively carried out in the literature for various fading statistical models, including Rayleigh, Rician, Nakagami-m, Weibull, lognormal distributions, assuming independent or correlated fading[5]-[13].

While most of the research on the performance achieved by various diversity techniques has been based on investigating the Bit Error Rate(BER) independently for several modulation schemes, [8] presented an effective BER performance analysis for the different diversity techniques, including MRC and SC, by applying the unified approach devised by Wojner in [5]. The unified approach can simplify the formulation of conditional BER of various binary modulation schemes in terms of the well-known gamma function as well as the incomplete gamma function, which enables us to derive concise and exact formulas of the average BER for MRC and SC diversity techniques with binary signaling over Rayleigh fading environments. Therefore, by judiciously exploiting the existing BER expressions given in [8], the aim of this paper is to derive simple but efficient asymptotic BER formulas for L-branch MRC and SC diversity techniques with binary signaling, and the corresponding asymptotic coding gains and diversity orders achieved by the MRC and SC schemes. Then, we further formulate the asymptotic SNR performance loss[10]-[13] induced by the SC diversity with respect to (w.r.t.) the MRC diversity, which can quantitatively compare the BER performance gap between the two diversity techniques adopting various binary modulation and detection schemes over Rayleigh fading channels. In particular, we obviously present the SNR performance gap in dB between MRC and SC techniques is only the function of the number of diversity branch, regardless of detection and modulation parameters.

This paper is organized as follows. In Section 2, a general formula of conditional BER of binary signaling and exact BER expressions for L-branch MRC and SC are presented. In Section 3, we provide comprehensive asymptotic performance evaluations including asymptotic BER formulas, coding gain, diversity order, and relative SNR performance loss of SC w.r.t. MRC over Rayleigh fading environments. Several numerical results are provided and discussed in Section 4. Then, some concluding remarks are drawn in Section 5.

Ⅱ. Exact BER Performance Analysis

According to the previous works in [1] and [8], a general formula for conditional BER of binary signaling for a given instantaneous SNR γ can be written as

where Γ(x,y) stands for the incomplete gamma function[14][15], Γ(x) is the gamma function, and p and q denote the parameters that define the types of detection and modulation, respectively, as (p, q) = (1, 0.5) for non-coherent binary frequency shift keying (NCBFSK), (p, q) = (1, 1) for differential binary phase shift keying (DBPSK), (p, q) = (0.5, 0.5) for coherent binary phase shift keying (CBPSK), and (p, q) = (0.5, 1) for binary phase shift keying (BPSK)[1][8].

Thus, the average BER can be obtained by integrating Eq. (1) w.r.t. the probability density function (pdf) or cumulative distribution function (cdf) of γ (i.e., f_γ(γ) or F_γ(γ)) as

where $$ P_b^{\prime }\left(\gamma \right)$$ is the first derivative of P_b(γ).

For L-branch MRC diversity in i.i.d. Rayleigh fading channels, the pdf of SNR γ is expressed by $$ f_{\gamma }^{\mathrm{M}\mathrm{R}\mathrm{C}}\left(\gamma \right)={\gamma }^{L-1}{\mathrm{e}}^{-\gamma /\overline{\gamma }}/\left(L-1\right)!{\overline{\gamma }}^L$$ with γ ≥ 0. Then, we can have the average BER expression as[8]

where ₂F₁(a,b;c;z) is the Gauss hypergeometric function, the definition of which is given in Eq. (07.23.02.0001.01)[15].

For L-branch SC diversity, the cdf of γ is given by $$ F_{\gamma }^{\mathrm{M}\mathrm{R}\mathrm{C}}\left(\gamma \right)={\left(1-e^{-\gamma /\overline{\gamma }}\right)}^L=\sum _{k=0}^L\left(\genfrac{}{}{0pt}{}{L}{k}\right){\left(-1\right)}^k{e}^{-k\gamma /\overline{\gamma }}$$ with γ ≥ 0, and the corresponding average BER expression of SC is given as[8]

ⅡI. Asymptotic BER Performance Analysis

3.2 Asymptotic SNR performance loss analysis

The asymptotic error rate is known to be expressed as $$ {\overline{P}}^{\mathrm{\infty }}={\left(G^{\mathrm{\infty }}\cdot \overline{\gamma }\right)}^{-d^{\mathrm{\infty }}}$$at high SNR, where G^∞ and d^∞ are the asymptotic coding gain and the asymptotic diversity order, respectively[1]. More specifically, G^∞ represents the horizontal shift in the error rate performance relative to the benchmark curve $$ {\overline{P}}^{\mathrm{\infty }}={\left(G^{\mathrm{\infty }}\cdot \overline{\gamma }\right)}^{-d^{\mathrm{\infty }}}$$, and d^∞ reflects the diversity contribution from the adopted transmit and receive techniques, represented by the magnitude of the slope of the average BER versus SNR on a log-log scale in the high SNR regime. Thus, the asymptotic coding gain and diversity order of L-branch MRC can be given as

$\[ \begin{array}{c}{G}^{\mathrm{M}\mathrm{R}\mathrm{C},\mathrm{\infty }}={\left[\frac{\Gamma \left(L+q\right)}{2L{p}^L\Gamma \left(L\right)\Gamma \left(q\right)}\right]}^{-\frac{1}{L}}\\ d^{\mathrm{M}\mathrm{R}\mathrm{C},\mathrm{\infty }}=L\end{array} \]$

(7)

and the asymptotic coding gain and diversity order of L-branch SC is also given by

$\[ \begin{array}{c}{G}^{\mathrm{S}\mathrm{C},\mathrm{\infty }}={\left[\frac{\Gamma \left(L+q\right)}{2p^L\Gamma \left(q\right)}\right]}^{-\frac{1}{L}}\\ d^{\mathrm{S}\mathrm{C},\mathrm{\infty }}=L\end{array} \]$

(8)

From Eqs. (7) and (8), it is obvious that L-branch MRC and SC diversity schemes achieve the full diversity orders of L, and different values of coding gains. Therefore, we can finally compare the asymptotic relative BER performances between MRC and SC over Rayleigh fading channels by formulating the following asymptotic SNR loss [10]-[13] in dB, which is induced by the SC diversity w.r.t. the MRC diversity, with the help of some simple arithmetic manipulations, as

$\[ \begin{array}{c}{\mathrm{S}\mathrm{N}\mathrm{R}\_\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}}_{\mathrm{S}\mathrm{C}\mathrm{ }\mathrm{w}.\mathrm{r}.\mathrm{t}.\mathrm{ }\mathrm{M}\mathrm{R}\mathrm{C}}^{\mathrm{\infty }}\\ =10{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left[\frac{G^{\mathrm{M}\mathrm{R}\mathrm{C},\mathrm{\infty }}}{G^{\mathrm{S}\mathrm{C},\mathrm{\infty }}}\right]\\ =\frac{10}{L}{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left[\frac{\left(\frac{\Gamma \left(\mathrm{L}+\mathrm{q}\right)}{2{\mathrm{p}}^{\mathrm{L}}\Gamma \left(\mathrm{q}\right)}\right)}{\left(\frac{\Gamma \left(\mathrm{L}+\mathrm{q}\right)}{2\mathrm{L}{\mathrm{p}}^{\mathrm{L}}\Gamma \left(\mathrm{L}\right)\Gamma \left(\mathrm{q}\right)}\right)}\right]\\ =\frac{10}{L}{\log }_{10}\mathrm{L}\Gamma \left(\mathrm{L}\right)\left[\mathrm{d}\mathrm{B}\right]\end{array} \]$

(9)

Eq. (9) apparently shows that the SNR performance loss is the function of the number of diversity branch (i.e., L), regardless of detection and modulation parameters (i.e., p and q). More specific asymptotic SNR loss for various L is presented in Table 1, where we can see that the increase of L leads to the increase of the performance degradation of SC over MRC in the high SNR regime.

Table 1.

SNR_LoSSSC w.r.t. MRC∞ for various L

IV. Numerical Results

In this section, we attempt to investigate and compare the average BER performances achieved by L-branch MRC and SC diversity techniques adopting binary signaling (e.g., NCBFSK, CBFSK, DBPSK, and BPSK) over Rayleigh fading environments.

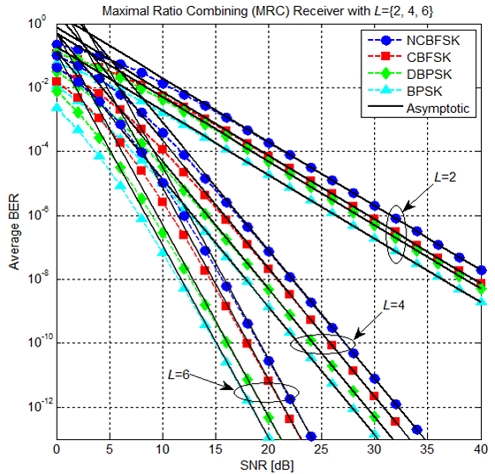
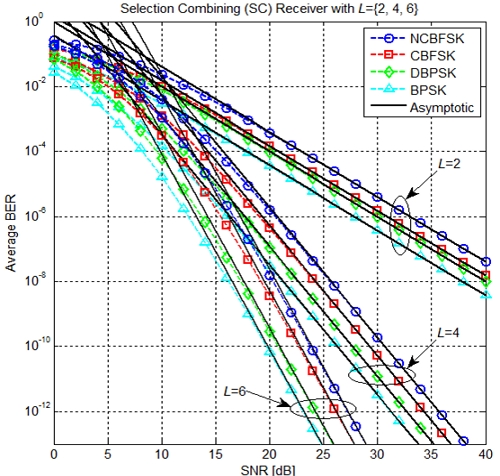
Figs. 1 and 2 show the average BER performances as a function of the average SNR $$ \overline{\gamma }$$ of MRC and SC diversity schemes, respectively, especially with different diversity branches L, over Rayleigh fading environments. For comparison purpose, we present the curves obtained from the exact BER expressions (i.e., Eq. (3) for MRC in Fig. 1, and Eq. (4) for SC in Fig. 2) together with the lines from our derived asymptotic BER formulas (i.e., Eq. (5) for MRC in Fig. 1, and Eq. (6) for SC in Fig. 2). From the figures, it is evident that the asymptotic lines show an excellent agreement with the curves from the exact BER formulas in the mid and high SNR regions.

Fig. 1.

Average BER vs. SNR of MRC with binary signaling and L = {2,4,6} over rayleigh fading channels

Fig. 2.

Average BER vs. SNR of SC with binary signaling and L = {2,4,6} over rayleigh fading channels

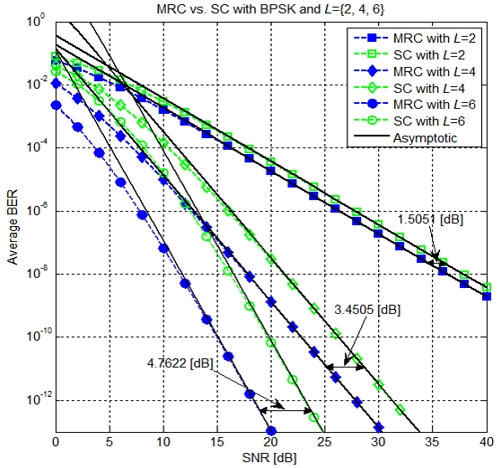
For the L-branch MRC and SC diversity schemes employing BPSK, the average BER vs. the average SNR $$ \overline{\gamma }$$ is depicted in Fig. 3. From this figure, we can first observe that the lines obtained from Eqs. (5) and (6) still very tightly converge to the curves from the exact BER expressions (i.e., Eqs. (3) and (4)) at high SNR. In addition, focusing on the asymptotic BER performance comparison between L-branch MRC and SC, which quantitatively depends on the number of L, as in Eq. (9), the figure obviously demonstrates that the asymptotic SNR losses for L = {2,4,6} is $$ {\text{SNR\_Loss}}_{\mathrm{S}\mathrm{C}\text{w.r.t.}\mathrm{M}\mathrm{R}\mathrm{C}}^{\mathrm{\infty }}=\left\{\mathrm{1.1501,3.4505,4.7622}\right\}$$, respectively, which exactly match with the values calculated from Eq. (9), also given in Table 1.

Fig. 3.

Average BER vs. SNR of MRC and SC with BPSK and L = {2,4,6} over rayleigh fading channels

V. Conclusions

We have first derived the asymptotic closed-form formulas of the average BER for MRC and SC diversity schemes adopting binary signaling over Rayleigh fading channels. Then, by judiciously exploiting the derived asymptotic BER expressions for MRC and SC, we have further obtained the corresponding asymptotic coding gains and diversity orders, and also formulated the asymptotic SNR performance loss of SC w.r.t. MRC in the high SNR region, which apparently shows that the asymptotic SNR loss is only dependent on the number of diversity branch. Finally, we have provided extensive numerical results to corroborate the exactness of our derived expressions.

Acknowledgments

This research was financially supported by Hansung University

References

• M. K. Simon and M.-S. Alouini, "Digital Communications over Fading Channels: A Unified Approach to Performance Analysis", 2nd ed. Hoboken, NJ, USA: John Wiley & Sons, 2005.
• G. L. Stüber, "Principles of Mobile Communications", Boston, MA, USA: Kluwer Academic Publishers, 1996.
• N.-S. Kim, "Performance of DOT relay system with MRC/GSC receiver in Rayleigh fading channels", Journal of IIBC, Vol. 12, No. 5, pp. 11-16, Oct. 2012. [https://doi.org/10.7236/JIWIT.2012.12.5.11]
• N.-S. Kim, "Performance of Opportunistic incremental NOMA relay systems in fading channels", Journal of IIBC, Vol. 16, No. 5, pp. 69-76, Oct. 2016. [https://doi.org/10.7236/JIIBC.2016.16.5.69]
• A. H. Wojnar, "Unknown bounds on performance in Nakagami channels", IEEE Trans. Commun., Vol. 34, No. 1, pp. 22-24, Jan. 1986. [https://doi.org/10.1109/TCOM.1986.1096424]
• J. Luo, J. R. Zeidler, and S. McLaughlin, "Performance analysis of compact antenna arrays with MRC in correlated Nakagami fading channels", IEEE Trans. Veh. Technol., Vol. 50, No. 1, pp. 267-277, Jan. 2001. [https://doi.org/10.1109/25.917940]
• G. K Karagiannidis, D. A. Zogas, N. C Sagias, S. A. Kotsopoulos, and G. S. Tombras, "Equal-gain and maximal-ratio combining over nonidentical Weibull fading channels", IEEE Trans. Wireless Commun., Vol. 4, No. 3, pp. 841-846, May 2005. [https://doi.org/10.1109/TWC.2005.846982]
• S. N. Datta, C. Bose, and A Chandra, "Unified analysis of error performance for binary signalling over Rayleigh fading channels", Electron. Lett., Vol. 43, No. 17, pp. 934-935, Aug. 2007. [https://doi.org/10.1049/el:20070732]
• S. Baek, S. Han, S. Lim, D. Kang, H. S. Oh, and C. Song, "Novel MRC packing channel estimation scheme for PER enhancement of IEEE 802.11p", Journal of KIIT, Vol. 16, No. 1, pp. 69-78, Jan. 2018. [https://doi.org/10.14801/jkiit.2018.16.1.69]
• X. Song, J. Cheng, and N. C. Beaulieu, "Asymptotic analysis of different multibranch diversity receivers with arbitrarily correlated Rician channels", IEEE Trans. Wireless Commun., Vol. 13, No. 10, pp. 5676-5689, Oct. 2014. [https://doi.org/10.1109/TWC.2014.2328993]
• X. Song, F. Yang, J. Cheng, and M.-S. Alouini, "Asymptotic SER performance comparison of MPSK and MDPSK in wireless fading channels", IEEE Wireless Commun. Lett., Vol. 4, No. 1, pp. 18-21, Feb. 2015. [https://doi.org/10.1109/LWC.2014.2359465]
• B. Zhu, "Asymptotic performance of composite lognormal-X fading channels", IEEE Trans. Commun., Vol. 66, No. 12, pp. 6570-6585, Dec. 2018. [https://doi.org/10.1109/TCOMM.2018.2863361]
• B. Zhu and Z. Zhang, "Asymptotic analysis on diversity receptions over fading channels with correlated shadowing", IEEE Trans. Veh. Technol., Vol. 68, No. 8, pp. 8275-8278, Aug. 2019. [https://doi.org/10.1109/TVT.2019.2926536]
• I. S. Gradshteyn and I. M. Ryzhik, "Table of Integrals, Series, and Products", 5th ed. San Diego, CA, USA: Academic, 1994.
• Wolfram functions site, http://functions.wolfram.com, . [accessed: Dec. 17, 2024]