고속 목표물 실시간 추적을 위한 FPGA를 이용한 병렬적 Huber 기반 확장 칼만 필터링

Ⅰ. 서 론

현대 유도무기에서 종말 호밍 유도 단계에서 탐색기 정보를 활용해 고속으로 이동하는 표적을 추적하고 요격하기 위해서는 시선 각속도를 정확히 추정해야 한다. 이를 위해 표적의 상태를 추정하는 필터의 성능이 매우 중요하며, 최근까지 고속 표적 추정 필터의 성능 향상을 위한 다양한 연구는 진행 중이다.

고속 표적 추정 필터의 성능을 개선하는 두 가지 방법이 있다. 첫째, 시스템 모델의 비선형성을 해결하여 성능을 향상시키는 방법[1]-[4], 둘째, 측정치의 비정규(Gaussian) 분포 오차에 대한 강건성을 높이는 방법[5[-[7]이다. 비선형성 문제를 해결하기 위해 다양한 접근법이 존재한다. 비선형 시스템을 1차 Taylor 급수를 이용해 선형화하는 확장 칼만 필터(EKF)[1], 샘플링 기반의 Unscented 칼만 필터(UKF)[2], Cubature 칼만 필터(CKF)[3] 등이 대표적이다. UKF는 Sigma 포인트를 이용해 Unscented 변환을 수행하며, CKF는 Sigma 포인트 대신 Cubature 포인트를 사용한다. 또한, 특정 경우에 한해 비선형 모델을 선형 모델로 변환하여 적용하는 변환 측정 칼만 필터(CMKF)[4]도 존재한다. 그러나 이러한 연구들은 시스템 모델의 비선형성을 다루는 데 집중되어 있으며, 대부분 필터의 비용 함수(Cost function)로 l2-norm을 사용하기 때문에 비정규 분포를 포함한 잡음(예: Impulsive 잡음, 혼합-Gaussian 잡음)에 대한 강건성이 부족하다. 이를 해결하기 위해 최근 연구에서는 l1-norm 또는 l2-norm과 l1-norm이 결합된 Huber 함수를 비용 함수로 적용하는 필터 기법이 제안됐다[5]-[7].

Huber 함수를 비용 함수로 사용하는 필터는 비정규 분포 잡음 환경에서도 기존 필터 대비 뛰어난 성능을 보인다[5]. 실제 시스템에서는 Gaussian 잡음만 존재하지 않기 때문에 필터의 강건성 확보가 필수적이다. 그러나 l2-norm이 아닌 다른 비용 함수를 사용하는 필터는 최적화 문제를 해결하기 위해 반복 계산을 수행하며, 수렴된 비용을 기준으로 상태변수를 추정한다. 이러한 반복 계산은 기존 l2-norm 기반 필터보다 연산량이 많아 실시간 처리가 어려운 단점이 있다.

이러한 실시간성 문제를 해결하기 위해 FPGA(Field Programmable Gate Array)나 GPU(Graphics Processing Unit)를 활용한 병렬 처리 기법이 연구가 진행됐다. GPU는 대규모 데이터를 병렬로 처리하여 연산 성능을 크게 향상시킬 수 있으며[8][9], FPGA는 하드웨어 수준에서 병렬 구조를 최적화하여 전력 효율성이 높고, 특정 연산에 최적화된 설계를 통해 실시간성이 요구되는 응용에 적합하다[10][11]. GPU는 연산 성능이 우수하지만 전력 소모가 크며, 반면 FPGA는 낮은 전력 소비가 가능하여 전력 제한 환경에서 활용된다[12].

본 연구에서는 Huber 기반 확장 칼만 필터(EKF)의 실시간성을 보장하기 위해 Huber 함수 계산 과정 일부를 FPGA에서 병렬화하는 기법을 설계하였으며, 알고리즘 수행시간을 분석하고 검증하였다.

2장에서는 Huber 함수 기반 EKF의 수행 구조와 실시간성 문제를 정의하며, 3장에서는 제안한 FPGA 기반 병렬화 기법의 전체 구조와 연산 최적화 방법을 설명한다. 마지막으로, 4장에서는 Huber 기반 EKF 알고리즘의 시뮬레이션 결과를 제시하고, 수행시간 분석 및 자원 사용량 평가를 통해 성능을 검증한다.

Ⅱ. 문제점 기술

탐색기 정보를 이용한 유도무기의 고속 표적 추정 필터의 교전 기하, 시스템 모델, 측정치 모델은 참고 문헌[13]을 참고하여 설명하고, Huber function 기반으로 하는 유도필터 구조에 대해서 추가하였다.

2.1 교전 기하

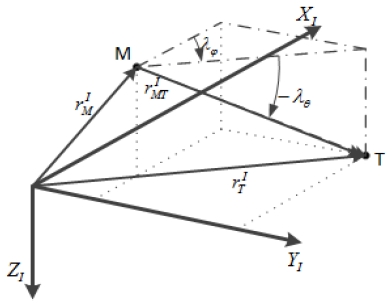
그림 1과 같이 관성좌표계(I)를 기준으로 하는 3차원 교전기하를 고려하자[13]. X_I, Y_I, Z_I 는 관성좌표계 축이고, $$ r_M^I{,r}_T^I$$ 각각은 관성좌표계를 기준으로 유도탄과 표적의 위치이다. $$ r_{MT}^I$$는 관성좌표계에서 표현된 유도탄에서 표적으로의 상대위치벡터를 의미하고, λ_φ는 X_I, Y_I 평면에서 표현된 유도탄과 표적 사이의 시선각, λ_θ는 X_I, Y_I 평면과 Z_i축이 이루는 면에서 표현된 유도탄과 표적 사이의 시선각을 나타낸다.

Fig. 1.

Engagement Geometry

2.4 Huber-based Extended Kalman Filter

본 절에서는 Huber function을 cost로 하는 HEKF(Huber based EKF)에 대해서 설명한다. 이를 위해 앞에서 설명한 시스템 모델 측정치 모델을 일반화된 형태로 나타내고 HEKF 적용에 필요한 변수들을 유도하였다. 유도된 변수들을 가지고 HEKF가 어떻게 적용되는지 Pseudo code 형태로 표현하였다.

식 (1), (6)의 시스템 및 측정치 모델을 일반화하여 표현하면 식 (7), (8)과 같다.

$\[ x_k=\Phi \left(t_k,t_{k-1}\right)x_{k-1}+w\left(t_k,t_{k-1}\right) \]$

(7)

$\[ z_k=h\left(x_k\right)+v_k \]$

(8)

$$ w\left(t_k,t_{k-1}\right)\sim N\left(0,Q\left(t_k,t_{k-1}\right)\right)$$, $$ v_k\sim N\left(0,R_k\right)$$는 각각 시스템 모델 불확실성과 측정치 잡음 오차이다. 추정 상태 변수의 오차와 분산을 $$ {\delta }_k=x_k-{\overline{x}}_k$$, $$ {\overline{P}}_k$$로 정의하고 측정치 모델을 추정 상태 변수 $$ {\overline{x}}_k$$에서 선형 근사화 하고 기존 상태 변수와 합치면 새로운 상태 변수를 얻을 수 있다.

$\[ \begin{array}{c}h\left(x_k\right)\approx h\left({\overline{x}}_k\right)+H_k\left(x_k-{\overline{x}}_k\right)\hfill \\ H_k={\frac{\partial h}{\partial x}\left|\mathrm{ }\right.}_{x=x_k}\hfill \end{array} \]$

(9)

$\[ \left[\begin{array}{c}{y}_k-h\left({\overline{x}}_k\right)+H_k{\overline{x}}_k\\ {\overline{x}}_k\end{array}\right]=\left[\begin{array}{c}{H}_k\\ I\end{array}\right]x_k+\left[\begin{array}{c}{v}_k\\ -{\delta }_k\end{array}\right] \]$

(10)

Whitening과 정규화를 위해 추가적으로 변수를 정의하였다.

$\[ T_k=\left[\begin{array}{cc}{R}_k& 0\\ 0& P_k\end{array}\right] \]$

(11)

$\[ d_k=T_k^{-1/2}\left[\begin{array}{c}{z}_k-h\left({\overline{x}}_k\right)+H_k{\overline{x}}_k\\ {\overline{x}}_k\end{array}\right] \]$

(12)

$\[ G_k=T_k^{-1/2}\left[\begin{array}{c}{H}_k\\ I\end{array}\right] \]$

(13)

$\[ {\xi }_k=T_k^{-1/2}\left[\begin{array}{c}{v}_k\\ -{\delta }_k\end{array}\right] \]$

(14)

$\[ d_k=G_k{x}_k+{\xi }_k \]$

(15)

여기서 T_k는 추정 오차와 측정치의 오차가 함께하는 분산 행렬, 제곱근은 Cholesky decomposition을 통해 획득 가능하다. d_k는 whitening, 정규화된 추정 상태 변수를 포함하는 측정치로 단위 분산 오차(ξ_k ~ N(0,1)) 특성을 가진다. G_k는 새롭게 정의된 측정치 행렬이다[5].

위 과정을 통해 도출된 상태변수는 아래의 Huber function기반의 cost를 최소로 해야 한다.

$\[ \begin{array}{c}J\left(x_k\right)=\sum _{p=1}^l\rho \left({\xi }_{k,p}\right)\hfill \\ \rho \left({\xi }_{k,p}\right)=\left\{\begin{array}{ccc}\frac{1}{2}{\xi }_{k,p}^2\hfill & \hfill & if\left|{\xi }_{k,p}\right|\le \gamma \hfill \\ \gamma \left|{\xi }_{k,p}\right|-\frac{1}{2}{\gamma }^2\hfill & \hfill & otherwise\hfill \end{array}\right.\hfill \end{array} \]$

(16)

ρ(•)는 Huber function, γ는 설계 파라미터이다. 위 cost function을 최소로 하는 상태변수를 찾기 위해서는 다음의 조건을 충족해야 한다.

$\[ \begin{array}{c}\sum _{p=1}^l{\rho }^{\prime }\left({\xi }_{k,p}\right)\frac{\partial {\xi }_{k,p}}{\partial x_k}=0\hfill \\ {\rho }^{\prime }\left({\xi }_{k,p}\right)=\Theta \left({\xi }_{k,p}\right)=\left\{\begin{array}{ccc}{\xi }_{k,p}\hfill & \hfill & if \left|{\xi }_{k,p}\right|\le \gamma \hfill \\ \gamma \cdot sign\left({\xi }_{k,p}\right)\hfill & \hfill & otherwise\hfill \end{array}\right.\hfill \\ \psi \left({\xi }_{k,p}\right)=\frac{\Theta \left({\xi }_{k,p}\right)}{{\xi }_{k,p}}\hfill \\ =\left\{\begin{array}{ccc}1\hfill & \hfill & if \left|{\xi }_{k,p}\right|\le \gamma \hfill \\ \frac{\gamma }{{\xi }_{k,p}}\cdot sign\left({\xi }_{k,p}\right)\hfill & \hfill & otherwise\hfill \end{array}\right.\hfill \end{array} \]$

(17)

ψ(ξ_k,p)의 대각 행렬을 Ψ라고 정의하면, 식 (17)은 식 (18)과 같이 행렬 연산 형태로 표현 가능하다. 이때의 최적 해는 식 (19)와 같다.

$\[ G_k^T\Psi \left(G_k{x}_k-d_k\right)=0 \]$

(18)

$\[ {\hat{x}}_k^{\left(j+1\right)}={\left(G_k^T{\Psi }^{\left(j\right)}{G}_k\right)}^{-1}{G}_k^T{\Psi }^{\left(j\right)}{d}_k \]$

(19)

이를 Pseudo code형태로 나타내면 표 1과 같다.

Table 1.

Huber-based extended Kalman Filter

Ⅲ. 제안하는 기법

3.1 전체 구조

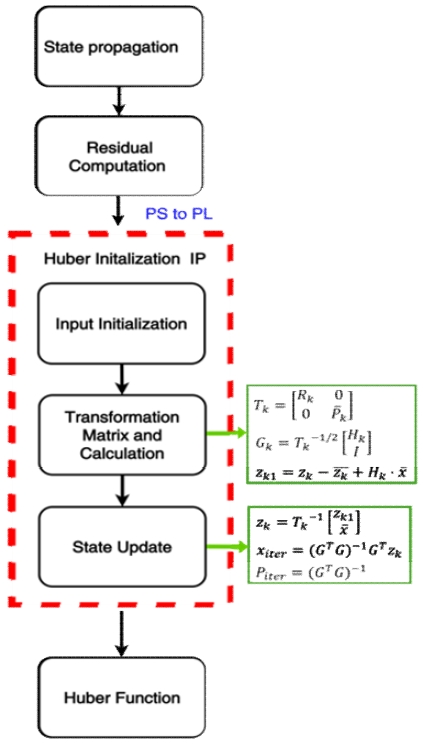
그림 2는 FPGA 기반으로 가속화된 Huber 기반 확장 칼만 필터의 전체 구조를 나타낸다. 이 구조는 PS(Processing System)와 PL(Programmable Logic) 간의 데이터 전송 및 병렬 연산을 통해 계산 효율을 극대화하도록 설계되었다. Huber Initialization의 주요 연산은 입력 데이터 초기화, 변환 행렬 계산, 상태 갱신으로 구성된다. Input Initialization 단계에서는 입력 데이터를 초기화하여 데이터를 BRAM에 저장한다. Transformation Matrix and Calculation 단계에서는 T_k의 Cholesky 분해를 통해 하삼각 행렬을 계산하고, 이를 기반으로 변환 행렬 𝐺를 생성한다. State Update 단계에서는 z_k, x_iter, P_iter를 계산하여 상태를 갱신한다. 갱신된 값은 Huber Fuction의 입력값으로 전달하여 PS와 PL 간의 상호 데이터 교환을 통해 동작한다.

Fig. 2.

Structure of Huber Initialization IP

3.2 연산시간 프로파일링

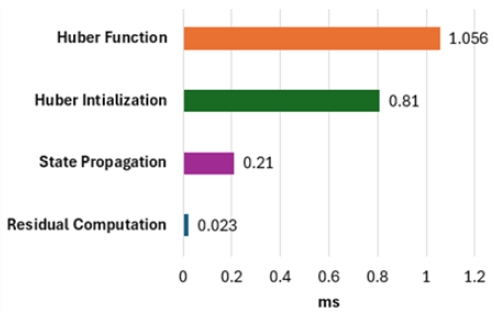
그림 3은 Huber 기반 확장 칼만 필터에서 각 연산이 차지하는 수행시간을 나타낸다. 가장 많은 시간을 차지하는 연산은 Huber Function으로, 약 1.056ms 가 소요되며 전체 연산의 주요 병목으로 작용한다.

Fig. 3.

Profiling of Huber-based EKF algorithm

두 번째로 높은 비중을 차지하는 연산은 Huber Initialization 계산으로, 약 0.81ms 가 소요된다. 그 외의 연산으로는 State propagation이 약 0.21ms로 상대적으로 낮은 비중을 차지하며, 상태 예측 과정에서 수행된다. 마지막으로 Residual 계산은 약 0.023ms로 전체 연산 중 가장 낮은 비중을 차지한다. 본 연구에서는 수행시간이 두 번째로 높은 Huber Initilization 계산에 병렬화 기법을 적용하였다. 이를 통해 FPGA 내부에서 Cholesky 분해 및 역행렬 계산과 같은 복잡한 연산과 행렬곱셈을 병렬적으로 수행하도록 설계하였다. 이러한 병렬화 작업은 Huber Initialization 계산에 드는 시간을 단축하여 전체 알고리즘의 실시간성을 크게 향상시킨다.

3.3 FPGA 기반 행렬곱셈 병렬화

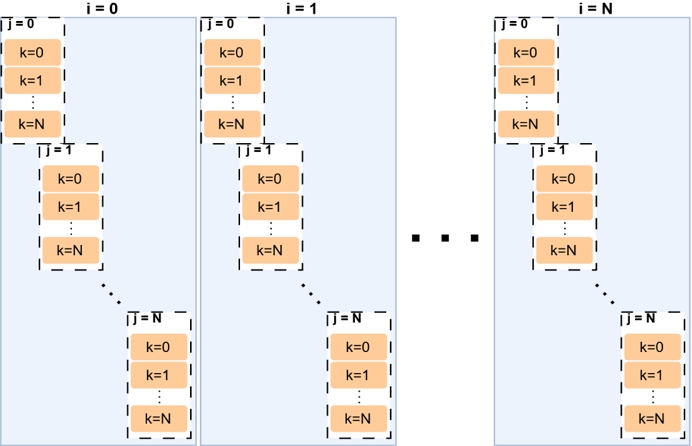
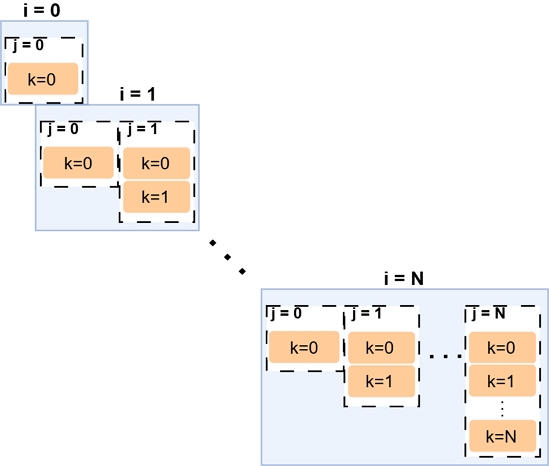
그림 4는 기존 행렬 곱셈에서 사용하는 3중 루프 구조를 나타내며, 그림 5는 이를 개선한 병렬화된 행렬 곱셈 구조를 보여준다. 기존 방식인 그림 4에서는 𝑖루프, 𝑗루프, 𝑘루프가 순차적으로 실행되며, 각 단계의 연산이 순차적으로 수행하여 연산 수행시간이 느리다. 특히 𝑘루프는 가장 많은 반복으로 수행되기 때문에 연산 병목이 발생하며, 행렬 크기가 커질수록 수행시간이 비효율적으로 증가한다.

Fig. 4.

Original matrix multiplication structure

Fig. 5.

Parallelized Matrix Multiplication Structure

반면 그림 5에서는 이러한 3중 루프를 병렬화 기법을 통해 최적화했다. 𝑘루프를 언롤링 기법으로 풀어서 각 요소를 동시에 계산하도록 설계했다. 이를 통해 반복적으로 수행되던 𝑘루프의 연산을 병렬적으로 처리하여 수행시간을 크게 단축했다. 또한 𝑗루프는 파이프라이닝 기법을 적용하여 각 반복을 한 사이클마다 처리했다. 이 방식은 𝑗루프 사이의 데이터 흐름을 최적화해 각 연산이 병렬적으로 실행되도록 한다.

결과적으로, 𝑖루프는 최상위 루프로써 순차적으로 진행되지만, 내부의 𝑗루프와 𝑘루프는 병렬 연산이 가능하다.

3.4 FPGA 기반 Cholesky 분해 병렬화

Cholesky 분해에서 사용하는 반복문 구조는 연산의 효율성을 크게 좌우한다. 그림 6은 기존의 3중 루프 구조를 기반으로 한 Cholesky 분해 방식을 나타낸다. 이 구조에서는 가장 바깥쪽 루프인 𝑖루프가 순차적으로 실행되며, 그 안에서 𝑗루프와 𝑘루프가 반복적으로 수행한다. 𝑖루프가 증가할수록 k와 j의 루프 반복도 증가한다. 특히, 𝑘루프는 반복 횟수가 가장 많아 연산 병목 현상이 발생하며, 행렬의 크기가 커질수록 수행시간이 비효율적으로 증가하는 문제가 있다. 이는 𝑘루프가 연산 대부분을 차지하며 순차적으로 실행되기 때문이다.

Fig. 6.

Original Cholesky decomposition loop structure

반면, 그림 7은 병렬화 기법을 통해 최적화된 Cholesky 분해 구조를 보여준다. 이 구조에서는 기존의 𝑘루프를 언롤링(Unrolling)하여 각 반복을 병렬 수행했다. 이를 통해 반복적으로 수행되던 𝑘루프의 연산을 동시에 처리하여 전체 수행시간을 크게 단축했다. 또한 𝑗루프에는 파이프라이닝 기법을 적용하여 각 반복을 한 사이클마다 처리할 수 있도록 최적화했다. 이를 통해 𝑗루프 내의 데이터 흐름을 개선하고, 연산이 병렬적으로 실행되도록 했다. 최적화된 구조에서는 𝑖루프는 여전히 순차적으로 진행되지만, 내부의 𝑗루프와 𝑘루프는 병렬화 및 파이프라이닝 기법을 적용해 효율적으로 실행된다.

Fig. 7.

Parallelized Choleky decomposition loop structure

Ⅳ. 결 과

4.1 환경 셋업

제안된 방법은 ARM Coretex-A53 프로세서 및 FPGA를 포함하는 Xilinx UltraScale+ MPSoC ZCU104 Evaluation Kit 보드 개발 환경에서 진행하였다. 제안한 기법의 성능을 비교하기 위한 시뮬레이션 조건은 다음 표와 같다.

사거리는 미사일과 표적의 초기 상대 거리를 의미한다. 이러한 시뮬레이션 구성을 통해 추적 필터를 이용하여 미사일과 표적의 상대위치 및 상대속도를 추정했다. 추정 결과를 바탕으로 표적 요격을 위한 미사일의 비례항법유도에 필요한 시선각속도를 산출하여 미사일이 표적을 요격할 수 있도록 시뮬레이션을 진행했다.

Table 2.

Simulation conditions

4.2 결과 및 분석

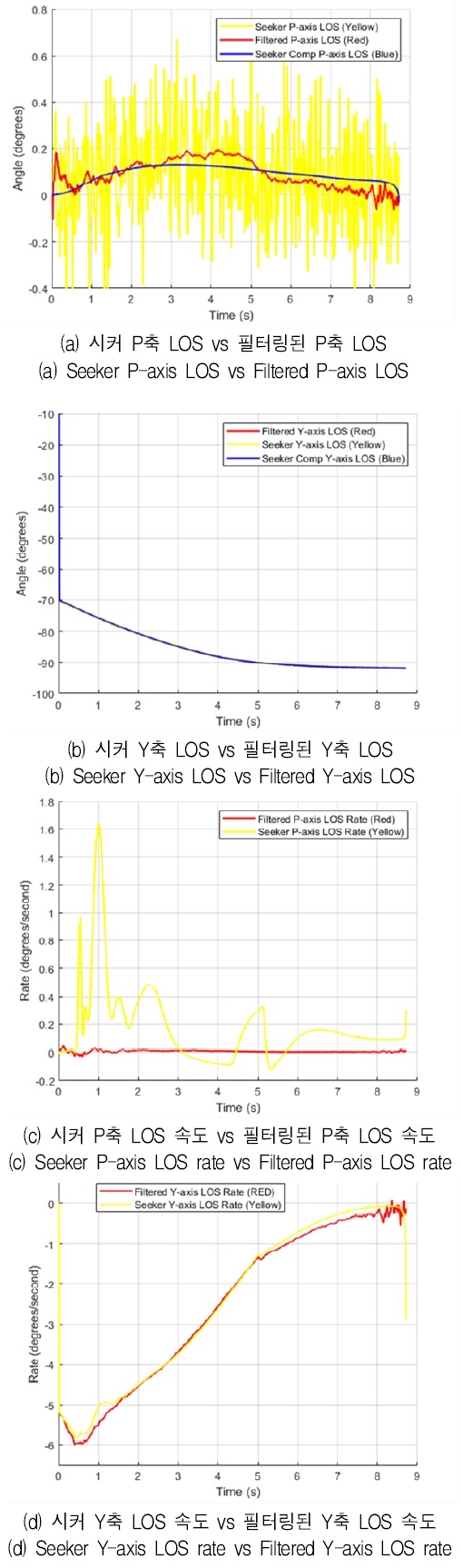
그림 8은 Huber 기반 확장 칼만 필터를 적용한 시뮬레이션의 결과를 보여준다. (a), (b)는 시선각 측정치(노란색)와 시선각 추정치(빨간색) 및 시선각 참값(파란색)을 보여주고 있다. (c), (d)는 시선각속도 추정치(빨간색)과 시선각속도 참값(노란색)을 보여준다.

Fig. 8.

Results of the proposed Huber-based EKF

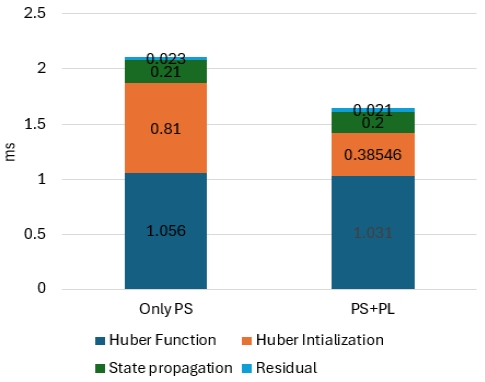
그림 9에서는 PS 단독으로 실행한 경우와 PS+ PL 구조로 연산을 수행한 경우의 수행시간를 비교한 그래프이다. PS만으로 연산을 수행한 결과 총 연산 시간이 2.099ms 소요되었고, 제안하는 PS+PL 구조를 통해 연산 시간이 1.674ms로 단축되었다.

Fig. 9.

Execution time comparison (Only PS vs. PS+PL)

이는 약 20.2%의 시간 절약을 의미한다. 특히, Huber Initialization 연산에서 수행시간이 0.81ms에서 0.385ms로 효과적으로 단축되었다. 이는 FPGA 기반 병렬화와 최적화된 하드웨어 구조가 연산 효율성을 크게 향상시켰음을 나타낸다. 결론적으로, 제안된 방법은 PS 단독 방식과 비교하여 계산 속도를 향상하며 동일한 수준의 필터링 성능을 유지하는 데 성공하였다.

자원적인 측면에서 표 3는 FPGA 자원 사용량을 나타내며 Look-Up Table (LUT)은 30.34%로 가장 높은 사용률을 기록하며, FPGA 내 연산 처리를 위한 주요 논리 요소로 활용되었다. LUTRAM은 10.14%, Flip-Flop (FF)는 12.79%로 사용되며 데이터 저장 및 동기화를 지원하였다. Block RAM (BRAM)은 1.92%로 메모리 저장, Digital Signal Processor (DSP)는 10.30%로 복잡한 연산 수행에 사용되었고, Global Buffer (BUFG)는 1.29%로 클럭 분배에 활용되었다. 이 결과는 FPGA 자원이 효율적으로 활용되었음을 보여준다.

Table 3.

FPGA resource utilization

Ⅴ. 결 론

본 연구에서는 Huber 기반 확장 칼만 필터의 실시간 처리를 개선하기 위해 FPGA 기반의 병렬 처리 기법을 적용한 하드웨어 구조를 제안하였다. 복잡한 연산인 행렬 연산을 병렬적으로 처리했다. 이러한 접근은 연산 과정에서 발생하는 병목 현상을 줄이고 실시간성을 크게 개선했다. 그 결과 기존 방식 대비 수행시간을 약 20.2% 개선했다. 제안하는 방법은 기존 방식과 비교하여 동일한 수준의 노이즈 제거 성능과 추정 정확도를 유지하면서, FPGA 기반 병렬화를 통해 연산 효율성을 높였다. 특히 Huber Initialization 연산 시간은 기존 PS를 통한 수행시간인 0.81ms에서 PS+PL을 통해 0.385ms로 단축되었다. 즉, 0.425ms의 수행시간 단축을 통해 약 52.47%의 감소를 달성했다. 향후 Huber Function 부분을 현재 IP 구조에 통합하고, Huber Filter 전 과정을 처리할 수 있는 단일 IP를 개발하는 방향으로 확장할 예정이다.

Acknowledgments

이 연구는 2025년도 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(No. KRIT-CT-22-024, 무장데이터링크/탐색기 종합 유도조종장치 모의기 설계 기술)

References

• D. Simon, "Optimal State Estimation-Kalman, H∞, and Non-linear Approaches", New Jersey, Jan. 2006. [https://doi.org/10.1002/0470045345]
• S. J. Julier and J. K. Uhlmann, "New extension of the kalman filter to nonlinear Systems", SPIE Proceeding, Orlando, FL, United States, Vol. 3068, pp. 182-193, Jul. 1997. [https://doi.org/10.1117/12.280797]
• I. Arasaratnam and S. Haykin, "Cubature Kalman filters", IEEE Transactions on Automatic Control, Vol, 54, No. 6, pp. 1254-1269, Jun. 2009. [https://doi.org/10.1109/TAC.2009.2019800]
• T. S. Schei, "A finite-difference approach to linearization in nonlinear estimation algorithms", Proc. American Control Conference Seattle, Seattle, WA, USA, pp. 114-118, Jun. 1995. [https://doi.org/10.1109/ACC.1995.529219]
• W. Li, M. Liu, and D. Duan, "Improved robust Huber-based extended Kalman filtering", Journal of Aeronautics, Astronautics and Aviation, Vol. 47, No. 1, pp. 41-48, May 2015.
• L. Chang, B. Hu, G. Chang, and A. Li, "Huber-based novel robust unscented Kalman filter", IET Science Measurement and Technology, Vol. 6, No. 6, pp. 502-509, Nov. 2012. [https://doi.org/10.1049/iet-smt.2011.0169]
• C. Tseng, S. Lin, and D. Jwo, "Robust Huber-based cubature Kalman filter for GPS navigation processing", Journal of Navigation, Vol. 70, No. 3, pp. 524-546, Oct. 2016. [https://doi.org/10.1017/S0373463316000692]
• J. Park, M. Lee, H. Lee, Y. Hwang, W. Choi, and B. Jeong, "Parallelized Monte Carlo Optimization With GPU for Real-time Ballistic Target Tracking", Journal of Institute of Control, Robotics and Systems, Vol. 29, No. 8, pp. 607-619, Aug. 2023. [https://doi.org/10.5302/J.ICROS.2023.23.0061]
• S. Lee, H. Lee, Y. Kim, J. Kim, and W. Choi, "GPU-Accelerated PD-IPM for Real-Time Model Predictive Control in Integrated Missile Guidance and Control Systems", Sensors, Vol. 22, No. 12, pp. 1-20, Jun. 2022. [https://doi.org/10.3390/s22124512]
• D. Kim, H. Lee, H. H. Kwon, Y. Hwang, and W. Choi, "Parallelized Particle Filter With Efficient Pipelining on FPGA for Real-Time Ballistic Target Tracking", IEEE Access, Vol. 11, pp. 104830-104838, Sep. 2023. [https://doi.org/10.1109/ACCESS.2023.3317896]
• J. Park, H. Lee, H.-H. Kwon, Y. Hwang, and W. Choi, "Parallelized Particle Swarm Optimization on FPGA for Realtime Ballistic Target Tracking", Sensors, Vol. 23, No. 20, pp. 1-18, Oct. 2023. [https://doi.org/10.3390/s23208456]
• Y. Ma, N. Suda, Y. Cao, J. Seo, and S. Vrudhula, "Scalable and Modularized RTL Compilation of Convolutional Neural Networks onto FPGA", Proceedings of the 26th International Conference on Field Programmable Logic and Applications (FPL), Lausanne, Switzerland, pp. 1-8, Sep. 2016. [https://doi.org/10.1109/FPL.2016.7577356]
• J. S. Park, Y. Y. Kim, S. H. Park, and Y. H. Kim, "Asynchronous guidance filter design based on strapdown seeker and INS information", Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 48, No. 11, pp. 873-880, Nov. 2020. [https://doi.org/10.5139/JKSAS.2020.48.11.873]
• A. K. Madsen, M. S. Trimboli, and D. G. Perera, "An Optimized FPGA-Based Hardware Accelerator for Physics-Based EKF for Battery Cell Management", Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, pp. 1-5, Oct. 2020. [https://doi.org/10.1109/ISCAS45731.2020.9181073]
• Z. Fan, K. Wang, M. Bao, and R. Li, "A Real-Time Hardware-Accelerator-Aided MJ-EKF SLAM Algorithm for Large-Scale Map Based on Heterogeneous Multi-Core SoC", Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, Singapore, 2023, pp. 1-7, Oct. 2023. [https://doi.org/10.1109/IECON51785.2023.10312111]
• D. T. Tertei, J. Piat, and M. Devy, "FPGA Design and Implementation of a Matrix Multiplier Based Accelerator for 3D EKF SLAM", Proceedings of the International Conference on ReConFigurable Computing and FPGAs (ReConFig14), Cancun, Mexico, pp. 1-6, Dec. 2014. [https://doi.org/10.1109/ReConFig.2014.7032523]
• Z. Dai and L. Jing, "Real-Time Attitude Estimation of Sigma-Point Kalman Filter via Matrix Operation Accelerator", Proceedings of the IEEE 13th International Symposium on Embedded Multicore/Many-core Systems-on-Chip (MCSoC), Singapore, pp. 342-346, Oct. 2019. [https://doi.org/10.1109/MCSoC.2019.00055]