소량의 정적 시험 데이터를 이용한 MEMS IMU 불량 검출 및 잔여 유효 수명 예측
초록
관성측정장치(IMU)는 이동체의 위치 추적 및 방향 감지 등에 필요한 핵심 부품으로 불량 혹은 성능 저하 시 관성항법시스템의 정확도를 크게 떨어뜨린다. 본 연구는 무인 이동체에 탑재된 MEMS IMU에 대해 정적 시험을 통해 얻은 시계열 데이터를 기반으로 항법 값의 드리프트를 일으키는 불량을 검출하고, IMU의 잔여유효수명(RUL)을 예측하는 방법을 제시한다. 제안 방법은 불량 검출의 정확도와 신뢰성을 높이기 위해 통계 기반 및 시계열 기반의 검출 모델을 사용한다. 특별히, IMU에 대한 시험 데이터를 지속적으로 수집하기 어려운 상황에서 소량의 다시점 시험 데이터를 활용하여 항법 드리프트 열화 모델을 구축하고 이를 기반으로 한 RUL 예측 방법을 제안한다. 성능 평가 결과 제안 기법은 우수한 불량 검출 정확도를 보였고, 딥러닝 기반 드리프트 열화 모델과 RUL 예측 모델은 양호한 결과를 나타내, IMU 예지 보전에의 적용 가능성을 보였다.
Abstract
Inertial Measurement Units(IMUs) are key components required for position tracking and direction sensing of a moving object, and their failure or performance degradation significantly reduces the accuracy of the inertial navigation system. This study presents a method to detect faults that cause navigation value drift and to predict the Remaining Useful Life(RUL) of an IMU based on time series data obtained through static tests for a MEMS IMU mounted on an unmanned vehicle. The proposed method uses statistical-based and time series-based detection models to increase the accuracy and reliability of fault detection. In particular, in situations where it is difficult to continuously collect test data for the IMU, a navigation drift degradation mode is constructed using a small amount of multi-time-point test data and an RUL prediction method based on that model is proposed. The performance evaluation results show that the proposed method exhibits excellent fault detection accuracy, and the deep learning-based drift degradation model and RUL prediction model delivered promising results, demonstrating the possibility of application to IMU predictive maintenance.
Keywords:
inertial measurement unit, fault detection, predictive maintenance, remaining useful life, degradation modelsⅠ. 서 론
센서는 사물인터넷(IoT), 헬스케어, 자율주행, 웨어러블 디바이스, 스마트 팩토리 등 다양한 산업 분야에서 물리적, 화학적, 생물학적 정보를 디지털 데이터로 변환하는 핵심 부품이다. 최근 센서 기술은 소형화, 고정밀화, 다기능화, 저전력화를 중심으로 발전하여 고성능 센서 개발을 가능하게 했으며, 이는 산업 전반의 시스템 성능 향상에 기여하고 있다. 특히, 반도체 공정을 기반으로 전자 및 기계적 구조를 융합한 MEMS(Micro-Electro-Mechanical Systems)[1] 기술은 초소형 센서의 대량 생산을 가능하게 함으로써 소형화와 비용 절감에 크게 기여하였으며, 이를 통해 다양한 환경에서 정밀한 데이터를 수집할 수 있는 고효율 시스템을 구현할 수 있게 되었다. 또한, 센서를 통해 수집된 대량의 정밀 데이터는 빅데이터 및 인공지능 기술과 결합하여, 시스템의 상태를 실시간으로 모니터링하고 데이터 분석을 통해 잠재적인 문제를 사전에 예측하는 예지 보전(Predictive maintenance) 등의 자동화 관리 기술에 기반을 제공하고 있다.
관성측정장치(IMU, Inertial Measurement Unit)는 가속도계(Accelerometer)와 각속도계(Gyroscope)를 통합하여 물체의 움직임과 자세를 측정하는 장치로 자율주행, 로봇, 항공, 방위 산업 등 다양한 산업에서 이동체의 위치 추적, 방향 감지, 속도 측정 등에 사용된다[2]. MEMS 기반 IMU는 소형화, 경량화, 저전력 소비 및 내구성의 장점으로 인해 다양한 소형 이동 장치에 널리 탑재되고 있다. 그러나 소형화와 비용 절감을 위한 설계로 인해 상대적으로 정확도가 떨어질 수 있다는 단점이 있다[3]. IMU는 제조 공정과 환경 요인의 영향을 받아 측정 오차가 발생할 수 있으며 이러한 오차를 보정하기 위해 오프셋 보정, 온도 보정 등 다양한 보정 기법이 적용된다. 그러나 IMU는 운용 과정에도 환경 조건 변화로 인해 바이어스 드리프트 증가와 같은 성능 저하 문제가 발생할 수 있다. 이러한 성능 저하는 센서 측정값의 정확도를 감소시켜 관성 항법 시스템(INS, Inertial Navigation System)의 성능을 떨어뜨릴 수 있다. IMU의 성능 유지는 정확한 측정값 확보를 위해 필수적이나, 이동체에 내장된 센서를 주기적으로 시험하고 보정하는 것은 높은 비용이 소요된다. 따라서 IMU의 상태를 확인하고 성능 저하를 예측할 수 있는 효율적인 오류 분석과 예지 보전 기술의 개발이 요구된다.
본 연구는 무인 이동체에 탑재된 MEMS IMU에 대해 정적 시험을 통해 얻은 데이터를 기반으로 항법 값의 드리프트(Drift)를 일으키는 불량을 검출하고, IMU의 잔여 유효 수명을 예측하는 방법을 제시한다. MEMS IMU의 상태를 평가하기 위해 이동체의 실제 동작 데이터를 사용하는 동적 시험은 이동체의 운용 데이터를 확보해야 하며, 높은 시험 비용과 복잡한 환경 조건이 요구된다. 반면, 이동체를 고정한 상태에서 센서 데이터를 수집하는 정적 시험은 비교적 저렴한 비용으로 안정적인 데이터를 확보할 수 있는 장점이 있다. 그러나 정적 시험은 수집할 수 있는 데이터의 범위가 제한적이며 신호 대비 잡음 비율이 높아 데이터 분석을 위한 정교한 모델 설계가 필요하다. 본 연구에서는 항법 드리프트를 일으키는 불량 IMU의 검출과 잔여 유효 수명 예측을 위해 다양한 예측 모델의 성능을 평가하고, 적은 횟수의 정적 시험을 이용해 IMU의 상태 관리와 예지 보전을 수행하는 방안을 제안하고자 한다.
본 논문은 다음과 같이 구성된다. Ⅱ절에서 본 연구의 주요 기술에 대한 기본 개념과 최근 연구 동향을 소개한 다음, Ⅲ절에서 제안 기법의 전체 구조 및 세부 내용을 설명한다. Ⅳ절에서는 제안 기법의 구현 방법과 학습 과정을 설명하고 Ⅴ절에서 성능 평가 결과를 고찰한 후 Ⅵ절에서 결론을 맺는다.
Ⅱ. 관련 연구
본 절에서는 본 연구와 관련된 주요 연구 동향을 IMU의 불량 특성 분석, 불량 진단 및 예지 보전 분야로 나누어 살펴보고 이를 본 연구에 활용할 가능성과 적용 방안 등을 검토한다.
2.1 IMU의 불량 특성
IMU 측정값은 일반적으로 센서 노이즈, 온도에 따른 스케일 팩터(Scale factor) 및 바이어스 변화와 같은 다양한 오류 원인에 의해 오염된다.
IMU 측정을 내비게이션 알고리즘에 통합하면 이러한 오류가 누적되어 위치 및 속도 출력에서 상당한 드리프트를 초래한다. IMU의 오류는 일정한 바이어스, 축 비직교성(Axis non-orthogonality), 축 정렬 불량 등으로 인해 발생하는 결정론적 오류와 노이즈와 같은 확률적 오류로 나눌 수 있다. 관성 센서의 확률적 노이즈를 모델링하기 위해 적응형 칼만 필터[4], 스펙트럼 밀도를 이용한 주파수 도메인 접근[5], 그리고 Allan Variance 기법[6] 등 다양한 방법이 개발되었다. 신호 처리 단계에서는 더 정확한 측정값을 얻기 위해 이러한 노이즈를 제거할 수 있는 웨이블릿(Wavelet) 디노이징[7]과 같은 스무딩 필터를 사용한다. 측정 각속도율(Measured angular rate) 와 측정 선형 가속도(Measured linear acceleration) , 이에 따른 정적 상태에서의 자세(Attitude) 오차 θerr와 속도 오차 Verr는 다음과 같다[8].
| (1) |
| (2) |
| (3) |
| (4) |
식 (1)~(4)에서 wt와 at는 각각 실제 각속도율과 실제 선형 가속도, bg와 ba는 시변(Time-varing) 바이어스, bg0와 는 각각 초기 바이어스 오차와 시변 바이어스 항, ηg와 ηa는 랜덤 가우시안 노이즈, k는 스케일 팩터, g는 중력가속도, ARW와 VRW는 각각 각도 및 속도 랜덤워크를 의미한다.
그동안 MEMS IMU의 항법 드리프트를 모델링하고 이를 동적으로 보상하기 위해 많은 연구가 수행되어왔다. 최근 Y.-H. Tu와 C.-C. Peng[9]은 MEMS 각속도계가 실리콘 구조로 온도변화에 민감한 문제를 해결하기 위해 온도 모델링 기술과 ARMA(Auto-Regressive Moving Average)를 이용한 실시간 드리프트 사전 보정 기술을 제안하였다. Y. Liu et al.[10]은 저비용 MEMS IMU 각속도계의 성능 향상을 위해 데이터 기반의 노이즈 제거 기법을 제안하였다. 이들은 어텐션(Attention) 메커니즘을 가지는 CNN(Convolutional Neural Networks)-LSTM(Long Short-Term Memory)을 이용하여 각속도 데이터에서 노이즈를 제거하여 바이어스 불안정성과 각도 랜덤워크를 감소시켰다.
한편, MEMS 장치는 보통 두꺼운 필름 및 얇은 필름을 포함하며, 실리콘, 금속, 유리 등 서로 다른 재료를 접합하여 제작하며 이 과정에서 발생하는 잔류 응력(Residual stress)은 MEMS 구조의 성능과 신뢰성에 크게 영향을 미친다[11]. N. Gupta et al.[12]은 잔류 응력이 질화 알루미늄 박막 기반 압전(Piezoelectric) MEMS 가속도계 구조에 미치는 영향을 분석하였다. 이 연구는 잔류 응력이 가속도계 구조의 모드 주파수를 크게 감소시켰으며, 구조 감도와 감쇄 계수(Damping factor)가 변경되고, 주파수 응답 대역폭이 감소하였음을 보였다. M. Hosseini-Pishrobat et al.[13]은 MEMS 링 각속도계에서의 응력에 따른 강성 분포의 변화를 수학적으로 설명하는 분석 모델을 제시하였다. 이러한 연구들은 장기 드리프트의 원인을 분석하고 응력이 유발하는 오류를 보정할 수 있는 기반을 제공하였다.
2.2 IMU 불량 진단
본 연구는 항법 값의 드리프트 오차를 유발하는 IMU의 불량에 대한 진단을 목표로 한다. 항법 값은 항법 시스템의 운용을 통해 얻을 수 있으나 IMU 외에 다른 측정장치를 사용하지 않을 경우, 동적 상황에서 불량 유무를 확인하기는 어렵다. 이를 해결하기 위해 최근 센서 데이터를 기반으로 한 불량 진단 기법이 제안되고 있다.
Y. Zhang et al.[14]은 심층신경망 비행체 IMU 센서의 불량 검출하는 방법을 제안하였다. 저자들은 다양한 비행 조건을 시뮬레이션할 수 있는 데이터 세트를 구성하고 CNN-LSTM 결합 모델에 비행 데이터를 입력하여 20가지 고장 사례에 대해 높은 검출 정확도를 달성하였다.
M. Crispoltoni et al.[15]은 퍼지 간격 모델(FIM, Fuzzy Interval Models)과 신경망을 결합한 IMU의 불량 검출 기법을 제안하였다. 제안 기법은 신경망을 센서 응답의 중앙값 예측에, FIM은 중앙 예측값 주변의 불확실성 포착에 활용하고 이를 선형 행렬 부등식의 최적화 문제로 구성하여 예측을 수행한다.
G. Xiang et al.[16]은 딥러닝 모델을 통한 IMU 불량 검출 성능을 향상하기 위해 시계열 데이터뿐 아니라 STFT(Short-Time Fourier Transform)을 이용한 주파수 성분 데이터를 사용하고 데이터 증강을 수행하는 데이터 전처리 기법을 제안하였다. T. Gao et al. [17]은 양방향 LSTM 기반의 EMD(Empirical Mode Decomposition)를 사용하여 IMU 센서 데이터를 힐버트(Hilbert) 스펙트럼으로 변환하는 EMD(Empirical Mode Decomposition) 기법을 제안하였다.
2.3 IMU 예지 보전 연구
시스템의 이상 징후를 사전에 파악하여 최적 시점(Optimal time)에서 유지보수를 수행할 수 있도록 하는 예지 보전 기술은 예측의 정확성을 확보하기 위해 RTF(Run-To-Failure) 또는 결함 진행 데이터가 필요하다. 그러나 이동체의 INS에서 IMU의 센서 데이터를 지속적으로 수집하는 것은 상당한 비용이 요구되므로 IMU에 대한 예지 보전 연구는 매우 제한적으로 이루어지고 있다. 예지 보전의 핵심 기술이라고 할 수 있는 잔여 유효 수명(RUL, Remaining Useful Life) 예측을 위해 필요한 데이터가 부족할 경우 시스템의 성능 저하 또는 열화(Degradation) 모델을 활용할 수 있지만, IMU 센서의 열화 모델에 관한 연구도 매우 부족한 상황이다.
V. Muthusamy와 K. D. Kumar[18]는 위성의 제어 모먼트 각속도계(control moment gyroscopes, 이하 CMG)의 고장 및 RUL 예측을 위해 위성 동역학의 CMG 스핀 모터에 결함을 유도하여 시스템의 RTF 데이터를 생성하였다. 또한 시스템의 고장 경로를 모델링하여 이를 사전 정보로 활용하고 베이지안(Bayesian) 업데이트 기법을 통해 실시간 RUL을 추정하였다. L. Tian과 Z. Wu[19]는 CMG의 운용 과정에서의 열화 단계를 통계적 프로세스 제어(Statistical process control)를 사용해 분석하고 Wiener 프로세스 기반 열화 모델을 제안하였다. 또한 열화 모델의 매개변수를 통해 열화 진행 상황을 정량화하고 이를 기반으로 RUL을 예측하였다. 그런데 이러한 방법들은 시험 데이터가 충분히 확보되었을 때 사용 가능하므로 본 연구에서와 같이 데이터가 부족할 때는 다른 접근 방법이 필요하다.
Ⅲ. 제안 기법
본 절에서는 IMU에 대한 소량의 정적 시험 데이터를 이용해 항법 값 드리프트 오류를 발생시키는 불량 검출 및 IMU의 RUL을 예측하는 방법을 제안한다.
3.1 전체 구조
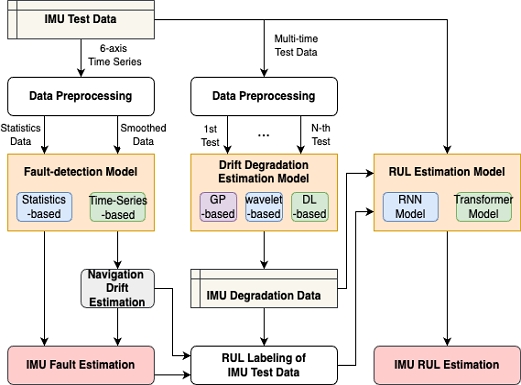
제안 기법은 그림 1과 같이 불량 검출 모델, 드리프트 열화 예측 모델 및 RUL 예측 모델을 중심으로 한 연계 구조로 이루어져 있다. 불량 검출 모델은 IMU 시험 데이터로부터 IMU의 불량을 예측하기 위한 모델이고, 드리프트 열화 예측 모델은 IMU의 RUL 라벨 생성을 위해 실제 시험 데이터로부터 항법 드리프트 열화를 예측하는 모델이다. 마지막 RUL 예측 모델은 IMU의 시험 데이터로부터 RUL을 예측하기 위한 모델이다.
IMU 시험 데이터는 정지 상태에서 일정 시간 동안 측정된 3축 가속도 및 각속도 데이터로 구성된다. 먼저, IMU 시험 데이터는 불량 검출 모델에 사용하기 위해 통계 데이터와 스무디드(Smoothed) 데이터로 전처리된다. 통계 데이터는 각 IMU의 6종 시계열 데이터에 대한 평균, 표준편차, 최댓값, 최솟값, 중앙값, IQR(Inter-Quantile Range), DC Offset 등의 통계 정보로 구성된다. 스무디드 데이터는 IMU 시계열 데이터의 노이즈 성분을 감소시키기 위해 각 시계열 데이터에 EWMA(Exponential Weighted Moving Average)를 적용한 값이다. 불량 검출 모델로는 통계 기반 모델과 시계열 기반 모델을 사용하는데, 각각 통계 데이터와 스무디드 데이터를 학습한다. 통계 기반 모델은 직접 IMU의 불량 여부를 예측하고, 시계열 기반 모델은 먼저 시계열 데이터로부터 항법 값의 드리프트를 예측한 후 이를 기반으로 IMU의 불량을 예측한다.
IMU의 항법 드리프트 열화를 예측하기 위해서는 단일 IMU에 대한 다시점(Multi-time-point) 시험 데이터가 필요하다. 본 연구는 가상 열화 데이터 생성을 위해 가우시안 프로세스(GP, Gaussian Process) 모델, 웨이블릿 기반 보간(Interpolation) 기법, 딥러닝 기반 열화 예측 모델을 데이터 상황에 따라 선택하여 사용한다. 열화 예측 모델에 의해 생성된 열화 정보를 이용해 IMU의 실제 시험 데이터에 RUL 라벨을 부여한다. 마지막으로, RUL 라벨이 부여된 각 IMU 시계열 데이터를 딥러닝 회귀 모델로 학습하여 RUL 예측을 수행하게 된다.
3.2 IMU 불량 검출
본 연구에서는 정지 상태의 시험 데이터를 사용하므로 IMU의 불량을 정지 상태에서의 6축(Roll, Pitch, Yaw, North, East, Down) 항법 값 드리프트 오차가 특정 문턱값 이상인 경우로 한정한다. 식 2와 4에서 IMU의 항법 드리프트를 유발하는 주된 요인은 가속도 및 각속도 값의 바이어스와 각도 및 속도 랜덤워크(ARW, VRW)이다. 이러한 항법 드리프트를 유발하는 특징을 포착하기 위해 데이터 학습 모델로 통계 기반 모델과 시계열 기반 모델을 사용한다.
통계 기반 모델은 6종 시계열 데이터로부터 바이어스와 랜덤워크 특징을 포착하는 통계 정보를 추출하고 이를 머신러닝 모델로 학습하여 불량을 예측한다. 바이어스는 시불변 바이어스 오프셋과 시변 바이어스로 나눌 수 있는데 시불변 성분은 시계열의 평균값과 중앙값으로, 시변 성분은 표준편차와 IQR을 이용해 그 성질을 파악할 수 있다. 랜덤워크 성분은 일종의 노이즈 성분으로 볼 수 있는데 통계 모델에서는 이에 대한 정보를 구체적으로 반영하기 어려우므로 노이즈를 감소시키기 위한 전처리를 수행하지 않고 원래의 측정 데이터로부터 통계 데이터를 생성한다. 추가로 랜덤워크의 주파수적 특징을 포착하기 위해 푸리에 분석을 수행하였는데 DC 성분을 제외하고 나머지 주파수 영역에서는 거의 고른 진폭을 보여 드리프트에 따른 주파수 스펙트럼에서 특이 사항을 발견하지 못하였다. 이에 학습 대상 통계 정보로 IMU 별로 다른 값을 보이는 DC 오프셋 값을 추가하였다.
통계 정보를 학습하여 불량 여부를 분류하는 모델로는 비교적 간단한 머신러닝 모델을 사용하였다. 표 형식(Tabular)의 데이터에서는 트리 기반 모델이 딥러닝 모델보다 우수한 성능을 보여준다는 연구 결과[20]를 바탕으로 머신러닝 모델로 결정 트리(Decision tree) 모델을 사용하였다. 통계 기반 모델은 학습을 통해 우수한 분류 성능을 보여줄 수 있으나 데이터가 충분치 않을 경우, 과적합 될 수 있다. 특히 트리 기반 모델은 입력 데이터를 특정 경곗값을 기준으로 나누기 때문에 예측 대상 데이터가 학습 데이터로 설정한 경곗값 근처에 있는 경우 성능이 불안정해질 수 있는 위험이 있다. 이를 보완하기 위해 본 연구에서는 추가로 시계열 기반 불량 예측 모델을 사용하였다.
시계열 기반 불량 예측 모델은 6종의 IMU 시계열 데이터를 입력받아 6축 항법 드리프트 오차를 예측하는 모델이다. 6축 항법 값은 시계열 데이터의 각 시점(Time point)에서 계산되나, 계산식을 사용하지 않고 매 시점의 항법 값을 예측하는 것이 많은 학습 데이터를 요구하기 때문에, 본 연구에서는 시험 데이터의 드리프트 오차 계산에 필요한 정보인 각 축에 대한 항법 값의 시작 값과 종료 값만을 예측하도록 하였다.
드리프트 오차를 직접 예측 대상으로 하지 않은 이유는, 비슷한 드리프트 오차 값을 가지는 시험 데이터들의 시작값이 서로 크게 차이가 나는 경우가 많아 이러한 특성을 학습할 수 있도록 하기 위함이다. 시계열 기반 불량 예측 모델로는 다양한 딥러닝 기반 시계열 데이터 회귀 모델의 성능을 평가하여 테스트하여 가장 우수한 예측 성능을 보인 모델을 LSTM 기반 모델을 사용하였다. 식 (5)는 시계열 기반 불량 예측 모델 Dθ의 수식을 보여준다.
| (5) |
식 (5)에서 fxyz(t)와 wxyz(t)는 각각 시험 시점 t에서의 가속도 및 각속도 시계열 데이터를, di(t)와 de(t)는 각각 시험 시점 t에서의 6축 항법 드리프트 시작값과 종료값 벡터를 의미한다.
3.3 드리프트 열화 예측
IMU 제품의 열화 모델을 구성하기 위해 RTF 데이터가 존재하지 않으면 센서 데이터의 시간적 변화 추이를 포착하기 위해 최대한 많은 시점에서의 시험 데이터가 필요하다. 그러나 주기적으로 시험 데이터를 수집하는 것은 현실적으로 어렵기 때문에 주어진 소량의 다시점 시험 데이터로부터 상황에 따라 선택할 수 있는 복수의 열화 모델을 제안한다.
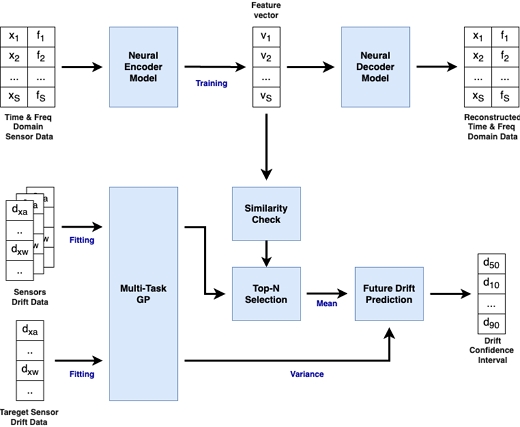
첫 번째 열화 모델은 전통적으로 열화 모델로 많이 사용되어 온 GP 모델로, 다시점 시험 데이터를 이용해 센서 데이터의 변화에 대한 예측과 불확실성을 포착한다. 다만 GP 모델은 커널 함수와 매개변수의 최적화가 쉽지 않고 시험 데이터의 수행 시점이 다양하지 않을 때 불확실성이 너무 커져 정확한 예측이 어려워지는 문제가 있다. 본 연구에서는 6축 항법 값에 대한 결합 예측을 위해 Muti-Task GP(이하 MTGP)를 사용하고, 미래 시점의 특성 예측 시 유사한 열화 특성의 IMU 데이터를 사용하기 위해 시계열 및 주파수 데이터의 특징 벡터를 이용한 유사도 분석 정보를 예측에 활용하였다. 본 연구에서 사용한 GP 기반 IMU 항법 드리프트 열화 예측 과정은 그림 2와 같다.
시계열 및 주파수 데이터의 특징 벡터를 구하기 위해서 시계열 데이터용 오토 인코더를 사용하였다. 시계열 데이터와 주파수 데이터를 동시에 사용하기 위해 STFT를 사용하여 시계열 데이터와 동일한 크기의 주파수 데이터를 생성하였다. 각 IMU 제품은 생산 과정에서의 편차 및 보정 등으로 인해 개별적인 특성을 가지게 되는데, 전체 IMU 시험 데이터를 통합하여 사용하면 전체 IMU에 대한 통계적 특성만 학습되므로 개별적 특성에 따른 예측이 불가능해진다. 따라서 GP 기반 열화 예측에서는 개별 IMU에 대해 학습 모델을 구축하고 대상 IMU와의 유사성을 기반으로 예측 모델을 가중 선택한다. 일정 시점 이후의 예측 드리프트 오차의 평균(gpmean)과 표준편차(gpstd)를 구하는 수식은 식 (6)과 같다.
| (6) |
식 (6)에서 gp(i)와 gp(t)는 각각 기존 IMU와 대상 IMU의 가우시안 프로세스 모델을, s(t,i)는 기존 IMU와 대상 IMU의 시험 데이터 유사도를 의미한다. 단, 기존 IMU는 전체 N개의 IMU 중 유사도가 높은 NS(≪N)개를 선택하여 사용한다.
만약 각 IMU에 대해 가용한 시험 데이터의 수행 시점이 매우 적을 경우, 다른 성능 저하 모델을 사용할 수 있다.
본 연구에서는 웨이블릿 기반 시계열 보간 기법과 딥러닝 모델 기반 드리프트 오차 예측을 추가로 사용한다. 웨이블릿 기반 시계열 보간 기법은 IMU 시험 데이터를 사용하여 내삽(Interpolation) 또는 외삽(Extrapolation)을 통해 새로운 시계열 데이터를 생성하되 웨이블릿 변환을 이용해 다양한 주파수 대역을 보간에 반영하여 보다 자연스러운 시계열을 생성하는 방법이다. 보간 방법은 선형, 로그형, 지수형, S자형 등에서 선택하여 사용한다. 보간을 통해 생성된 특정 시점의 시계열 데이터에 3.2절의 불량 예측 모델을 적용하면 해당 시점에서의 드리프트 열화 정보를 얻을 수 있다.
딥러닝 모델 기반 드리프트 오차 예측 기법은 3.2절에서 제안된 시계열 기반 불량 예측 모델을 미래 시점의 드리프트 오차를 예측하는 모델로 확장한 것이다. 딥러닝 기반 드리프트 오차 예측 모델 D′θ은 식 (7)과 같이 표현될 수 있다.
| (7) |
식 (7)에서, Δt는 시험 시점 t 이후의 경과시간을 의미하고 di(t + Δt)와 de(t + Δt)는 각각 시점 t + Δt에서의 6축 항법 드리프트 시작 값과 종료 값 벡터를 의미한다.
딥러닝 기반 드리프트 오차 예측 모델은 시계열 데이터와 경과시간 정보를 함께 입력받는 멀티 모달 데이터 학습 모델이다. 본 연구에서는 기존 LSTM 기반 불량 예측 모델을 확장하여, LSTM 출력 표현에 Δt 데이터 입력에 대한 FC(Fully Connected) 계층의 출력 표현을 결합하여 예측을 수행한다. 식 (8)은 딥러닝 기반 드리프트 오차 예측 모델 D′θ의 모델 구성을 보여준다.
| (8) |
식 (8)에서, LSTM과 MLP는 각각 LSTM 모델과 MLP 모델을 의미하고, ∥는 벡터의 연결(Concatenation) 연산자이다.
3.4 RUL 예측
특정 IMU IMUi에 대해 시험 시점 t의 시계열 데이터로부터 일정 시간 Δt 후의 시계열 데이터를 생성하거나 직접 드리프트 열화 정보를 예측할 수 있으면 이를 이용해 t 시점에서의 가상 RUL 라벨 RUL(IMUi,t)을 생성할 수 있다. 생성 방법은 단순히 RUL의 시간 단위를 기준으로 Δt를 1부터 계속 증가시키면서 드리프트 예측 오차 가 불량 판정 문턱값 th을 초과하는 시점을 찾으면 된다. 즉, IMUi의 t 시점에서의 가상 RUL 값은 식 (9)와 같이 구할 수 있다.
| (9) |
식 (9)에서 는 t + Δt 시점에서 예측된 6축(nr, np, ny, nn, ne, nd) 항법 드리프트 예측 오차 중 하나를 의미한다. 불량 판정 기준 thi은 항법 값의 한 축에 대한 불량 판정 문턱값을 의미하며, 어느 축에 대해서라도 드리프트 예측 오차가 불량 판정 문턱값보다 커지는 최소 시간 Δt가 RUL이 된다.
RUL 예측 모델은 특정 시점에서의 IMU 시계열 데이터를 입력받아 그 시점의 RUL 값을 예측하는 모델로 일반적인 시계열 데이터 회귀 모델을 사용할 수 있다. RUL 예측 모델 학습을 위해 필요한 IMU의 시험 데이터가 부족할 경우, 3.3절에서 제시한 웨이블릿 기반 시계열 보간 기법 또는 TimeVAE[21]나 Diffusion-TS[22] 등과 같은 시계열 생성 모델을 활용하여 데이터 증강을 시도해 볼 수 있다. RUL 예측 모델로 실제 시험 데이터에 대해 가상 RUL 라벨을 예측할 수 있다면, 실제 시험 데이터에 해당 RUL 값을 예측할 수 있는 정보가 포함되어 있음을 의미하기 때문에 3.3절의 드리프트 열화 모델과 가상 RUL 라벨의 유효성을 간접적으로 보여줄 수 있을 것이다.
Ⅳ. 구현 방법
4.1 데이터 수집 및 전처리
수집된 IMU 시험 데이터는 총 12,228개로 미국 허니웰(Honeywell) 사의 MEMS IMU 10,597개로부터 얻어진 것이다. 각 시험 데이터는 IMU를 특정한 방향으로 정렬한 후 정지된 상태에서 100초간 100Hz 빈도로 수집하였으며, 가속도 3축, 각속도 3축으로 구성된 (10,001 시퀀스, 6 특징) 모양의 시계열 데이터이다. 수집된 데이터에는 하나의 IMU에 대해 최대 3번 시험 데이터가 존재하는데, IMU 기준 시험 데이터 수집 횟수의 분포는 표 1과 같다. 표 1에서 시험 횟수 산출 시 비숫한 시기에 여러 번 시험한 데이터는 제외하고 최소 1개월 이상의 간격으로 시험한 것만 다른 횟수로 간주하였다.
표 1의 통계에서 사용된 수집 횟수를 기준으로 IMU의 시험 시점 간 평균 기간은 32.8개월, 표준편차는 4.7개월로, 시험 시점 간의 시간 간격이 비교적 큰 데 비해 편차는 상대적으로 작은 편이라고 볼 수 있다.
정지 상태에서의 항법 드리프트 오차 기준 불량 판정 문턱값 th은 항법 6축 (nr, np, ny, nn, ne, nd)에 대해 각각 (3.33, 3.33, 3.33, 32.11, 32.11, 14.88)이다. 12,228개의 시험 데이터는 항법 드리프트 오차가 부여되어 있는데 173개의 시험 데이터가 불량에 해당하여 1.4%의 불량률을 보였다. IMU 기준으로는 33개의 IMU가 불량으로 판정되어 불량률이 0.3%로 매우 낮게 나타났다.
통계 데이터는 각 시험 데이터로부터 1차로 평균, 표준편차(σ), 최댓값, 최솟값, 중앙값, IQR(Inter-Quantile Range), DC Offset을, 2차로 2σ, 3σ 범위와 10%, 25%, 75%, 90% 분위값 및 시험 자세(Position) 정보를 추출하였다. 시계열 데이터의 스무딩에는 50 크기 윈도우의 EWMA를 사용하여, 원 시계열 데이터와 동일 크기를 가지는 스무디드 데이터를 생성하였다.
4.2 모델 구현 및 학습
시험의 통계 데이터를 사용하는 불량 검출 모델로 결정 트리(Decision tree)를 scikit-learn[23] 기반으로 구현하여 시험하였다. 결정 트리는 분류 방법에 대한 설명이 가능한 트리 기반 모델 중 가장 단순한 모델로 과적합을 피하는 데 도움이 된다. 12,228개의 시험 데이터를 학습 70%, 시험 30%로 분할하여 학습을 진행하였고, 5겹 교차검증을 수행하여 평균값을 사용하였다. 또한, 시계열 데이터 기반의 불량 검출 모델로 시계열 데이터를 학습할 수 있는 LSTM 모델을 tsai[24] 기반으로 구현하여 시험하였다. 12,228개의 시험 데이터 중 항법 드리프트 처음 값과 종료 값이 존재하지 않는 데이터를 제외한 총 11,509개의 시험 데이터를 7:3으로 나누어 학습과 시험에 사용하였다.
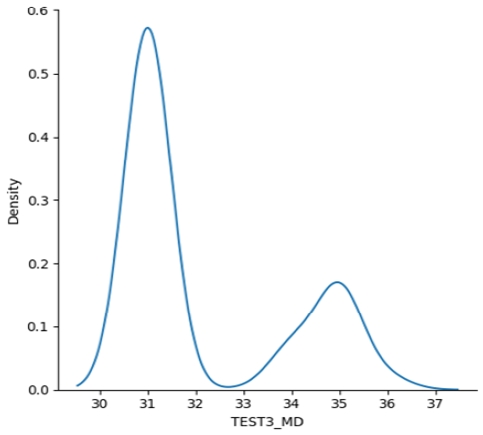
드리프트 열화 예측을 위해서는 다시점 시험 데이터를 사용해야 하는데 수집 데이터에는 다시점 데이터가 IMU 기준으로 6.7%밖에 되지 않았다. 이 중에서 시험 데이터의 드리프트 오차 라벨에 시작 값과 종료 값 정보가 없는 데이터와 시계열 및 드리프트 라벨에 이상치가 들어있는 데이터를 제외하고 최종 624쌍의 2회 시험 데이터를 학습 데이터로 선정하였다. 열화 모델 학습을 위해 선별한 2회 시험 데이터의 시험 간 시간 간격 분포는 그림 3과 같다. 각 열화 모델의 학습에는 전체 데이터의 70%를 사용하였고 나머지 30%로 성능을 평가하였다.
GP 기반 열화 예측 모델은 gpytorch 패키지[25]를 사용하여 구현하였고, MTGP 구현을 위해 다중 태스크 다변량 정규 분포와 촐레스키 변분 분포(Cholesky variational distribution) 및 마턴(Matern) 커널을 사용하였다. 한편, 시계열 시험 데이터의 특징을 추출하기 위한 시계열 오토 인코더에서는 200차원의 특징 벡터를 사용하였다.
보간 기반 열화 예측 모델에서 웨이블릿 변환에는 pywt 라이브러리[26]를 사용하였고, 보간 함수로는 선형 함수를 사용하였다. 딥러닝 기반 열화 예측 모델은 tsai를 기반으로 구현하였다.
RUL 예측 모델 구현에는 tasi 패키지를 사용하였고, RNN(Recurrent Neural Networks) 기반 모델과 Transformer 기반 모델을 시험하였다. 단, 학습 성능과 RUL 예측 값의 신뢰성을 높이기 위해 학습에 사용되는 손실함수를 기존 MSE(Mean Square Error) 또는 MAE(Mean Average Error) 대신 WMAE(Weighted MAE)와 AL(Asymetric Loss)를 정의하여 사용하였다. WMAE는 예측값이 정답 값 평균에 가깝게 있을 때 페널티를 부여하여 예측값이 고루 분포하도록 만들며, AL은 RUL 예측 이전에 정비가 이루어지도록 RUL 예측값이 정답 값보다 클 때 페널티를 부여한 것이다. 하나의 예측값 yi에 대한 WMAE 손실과 여기에 AL 손실을 적용한 최종 손실은 각각 식 (10), (11)과 같다. 식 (10)과 (11)에서, yi와 는 각각 정답 값과 예측값을, 는 정답 값의 평균을 의미한다.
| (10) |
| (11) |
RUL 예측 모델의 학습을 위해서는 RUL 라벨이 달린 시계열 시험 데이터가 필요한데, RUL 라벨링은 열화 예측 모델을 통해 수행되므로 RUL 예측 모델 학습에 사용된 1,248개의 시계열 데이터만 가상 RUL 라벨이 부여되었다. 학습 데이터가 충분하지 않지만, 별도의 데이터 증강은 사용하지 않고 시계열 데이터를 7:3으로 나누어 각각 RUL 예측 모델의 학습 및 시험 데이터로 사용하였다.
Ⅴ. 성능 평가
제안된 IMU 불량 검출 및 RUL 예측 기법에 대한 성능은 불량 검출 모델의 분류 정확도, 드리프트 열화 예측 모델의 예측 정확도, RUL 예측 모델의 예측 정확도를 기준으로 평가하였다.
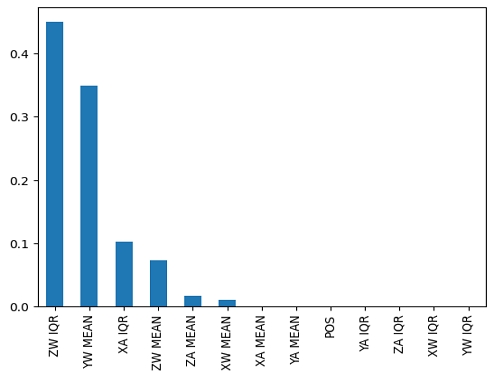
불량 검출 모델의 성능은 이진 분류 결과에 대한 정확도(Accuracy), 정밀도(Precision) 및 재현율(Recall)로 평가하였다. 또한, 평가지표 계산 시 불량을 양성(Positive)으로 놓고 평가하였다. 불량 검출을 위해 다양한 모델을 비교 평가하여 통계 기반 모델로는 가장 우수한 결과를 보인 결정 트리 모델을 사용하였고, 시계열 기반 모델로는 LSTMPlus[27]를 사용하였다. LSTMPlus는 LSTM 구조를 가지는 회귀 모델로 3계층 스택형 양방향 구조로 설정하였고, 각 계층의 은닉 노드 수는 200, 100, 50이다. 표 2는 통계 기반 모델과 시계열 기반 모델의 성능 평가 결과를 보여준다. 표 2의 결과에서 통계 기반 모델이 시계열 기반 모델보다 우수한 불량 검출 성능을 보여주었다. 이진 분류 환경에서 클래스 간 불균형이 매우 심해, 딥러닝 모델 학습에 필요한 불량 클래스 데이터가 충분하지 못하기 때문으로 판단된다. 통계 기반 모델은 과적합이 발생하지 않도록 모델 용량을 줄이기 위해 결정 트리 모델의 깊이를 10으로 제한하고, 학습에는 시험 데이터에 대한 통계 데이터 중 6축(XA, YA, ZA, XW, YW, ZW) 센서 데이터의 평균값(MEAN), IQR 및 자세 정보(POS)만 사용하였다.
그림 4는 통계 기반 모델의 학습 특징 중요도를 도시한 것이다. 전체 통계 정보 중 6개의 특징이 모델 구성에 사용된 것을 볼 수 있다. 시계열 기반 모델은 통계 기반 모델보다 성능이 떨어지지만, 과적합 가능성이 상대적으로 작으므로 학습 데이터가 충분할 경우 보조 모델 또는 앙상블 모델로 활용이 가능할 것이다.
드리프트 열화 모델 중 웨이블릿 변환 기반 보간 기법은 학습을 사용하지 않으므로 평가 대상에서 제외하였다. GP 기반 및 딥러닝 기반 열화 예측 모델의 성능 평가는, 학습할 수 있는 다시점 데이터가 두 개의 시점 데이터만 존재하는 상황이라 첫 시점의 드리프트 데이터만 학습에 이용해 두 번째 시점의 드리프트 오차를 예측하는 방식으로 진행하였다. 딥러닝 기반 열화 예측 모델은 LSTMPlus[27]를 사용하였다. LSTMPlus는 은닉 노드 수 200, 100을 가지는 2계층 스택형 양방향 구조로 설정하였다. 예측 정확도를 평가하는 기준은 식 (12)와 같은 NRMSE(Normalized Root Mean Square Error)를 사용하였다.
| (12) |
식 (12)에서, yi, 는 각각 정답 값과 예측값을, N은 시험 샘플 수를 의미한다. 표 3은 GP 기반 및 딥러닝 기반 열화 예측 모델의 성능 평가 결과를 비교한 것이다. 표 3의 평가 결과에서 딥러닝 기반 모델은 GP 기반 모델보다 우수한 열화 예측 성능을 보여주었다. GP 기반 모델의 성능이 떨어지는 것은 다시점 데이터가 단지 두 개의 시점 데이터로 구성되어 있기 때문에 예측 불확실성이 매우 커서 IMU 간 유사도를 활용하더라도 정확도 향상에 한계가 있기 때문으로 판단된다. nd축이 다른 축에 비해 예측 오차가 큰 것은 정지 상태에서 드리프트 변동이 거의 없어서 작은 예측 변동에도 오차가 커지기 때문이다.
다음으로 드리프트 열화 예측 모델에서 사용한 1,248개 학습 데이터에 대해 각 열화 예측 모델과 식 3-5를 사용하여 RUL을 생성하였다. 딥러닝 기반 열화 예측 모델을 이용한 RUL 예측에서는 추가로 Δt를 입력해야 하므로 시계열 데이터와 테이블형 데이터를 함께 사용할 수 있는 tsai의 MultiInputNet[28]을 사용하였다. 표 4는 열화 예측 모델이 예측한 RUL 값의 평균과 표준편차를 비교해 보여준다. 표 4에서 GP 기반 및 딥러닝 기반 열화 예측 모델이 예측한 RUL 값은 비교적 유사하지만, 웨이블릿 변환 기반 보간 기법은 RUL 값을 매우 크게 예측하였다. 웨이블릿 변환 기반 보간 기법은 개별 IUM에 대해 두 개의 측정값만으로 예측을 수행하므로 전체 IMU에 대한 통계적인 RUL 특성을 파악할 수 없어 예측 정확도가 낮은 것으로 보인다.
산업용 고정밀 IMU의 신뢰 수명이 10년 내외로 알려져 있는데 GP 기반 및 딥러닝 기반 모델이 예측한 수명은 비교적 이와 부합하는 예측값을 보여주었다. 본 연구에서는 드리프트 열화 예측에서 더욱 우수한 성능을 보여준 딥러닝 기반 열화 모델을 이용해 시험 데이터의 RUL 예측값을 부여하였다.
RUL 예측의 평가 지표로는 RUL 예측 오차와 함께 통상적으로 RUL 예측 정확도 평가에 사용하는 RUL 스코어 예측 오차의 정규화 식을 사용하였다. RUL 예측 오차와 RUL 스코어 예측 오차는 각각 식 (12)와 (13)을 사용하여 계산하였다.
| (13) |
식 (13)에서, yi와 각각 정답 값과 예측값을 N은 시험 샘플 수를 의미한다. RUL 예측 모델로는 tasi의 딥러닝 모델 중 RNN 기반 회귀 모델인 MGRU_FCNPlus[29]와 Transformer 기반 회귀 모델인 TSTPlus[30]를 선택하였다. MGRU_FCNPlus는 컨볼루션 계층과 Squeeze 및 Excitation 블록[31]이 포함된 GRU 기반 회귀 모델로 단일 GRU 계층과 은닉 노드 수 100개로 설정하였다. TSTPlus는 Transformer 기반 다변수 시계열 회귀 모델로 헤드 수는 4개, 모델의 차원 수는 32개로 설정하였다. RUL 예측 모델의 성능 평가 결과는 표 5와 같다.
Ⅵ. 결론 및 향후 과제
본 논문은 다양한 이동체에 탑재되어 항법 기능을 가능하게 하는 MEMS IMU 기기에 대해 정지 상태의 시험 데이터를 사용해 항법 드리프트 불량 여부와 RUL을 예측하는 방법을 제안하였다. 특별히, IMU에 대한 시험 데이터를 지속적으로 수집하기 어려운 상황에서 소량의 다시점 데이터를 활용하여 드리프트 열화 모델을 구축하고 이를 기반으로 RUL을 예측하는 방법론을 제시하였다. IMU의 열화 특성은 제품의 모델마다 다를 수 있으므로 제안된 방법을 활용하기 위해서는 단일 모델의 제품에 대해 충분한 양의 다시점 시험 데이터를 확보하는 것이 필요하다.
본 논문에서 제시된 열화 모델과 RUL 예측 모델을 실제 산업 분야에서 IMU의 예지 보전에 적용하기 위해 다음의 후속 연구를 진행할 예정이다. 먼저 MEMS IMU의 제조 과정에서 발생하는 응력 등 항법 드리프트 오차를 유발할 수 있는 요소에 대해 물리적 특성을 정확히 파악하여 이를 열화 모델 설계에 반영할 예정이다. 또한, 다양한 접근 방법을 통해 개발된 예측 모델을 앙상블하여 예측 성능과 신뢰성을 확보할 것이다. 추가로 다시점 시험 데이터가 부족한 상황에서, 상대적으로 데이터가 풍부한 단일 시점 데이터를 열화 모델 개발에 활용할 수 있는 방안을 모색할 것이다.
Acknowledgments
본 연구는 국방기술진흥연구소에서 지원하는 방산특화개발연구소 구축 및 운영 (No.DC2023SD)사업의 연구 수행으로 인한 결과물임
References
- K. J. Gabriel, "Microelectromechanical Systems (MEMS)", IEEE Transactions on Electron Devices, Vol. 43, No. 10, pp. 1626-1636, 1995.
-
J. Lee and W. C. Lee, "Position Calibration and Navigation of Mobile Robot Using Inertial Sensor and Fuzzy Rules", Journal of KIIT, Vol. 11, No. 5, pp. 25-31, May 2013.
[https://doi.org/10.14801/kiitr.2013.11.5.25]

-
J. Xuan, T. Zhu, G. Peng, F. Sun, and D. Dong, "A Review on the Inertial Measurement Unit Array of Microelectromechanical Systems", Sensors, Vol. 24, No. 22, pp. 7140, Nov. 2024.
[https://doi.org/10.3390/s24227140]

-
A. H. Mohamed and K. P. Schwarz, "Adaptive Kalman Filtering for INS/GPS", Journal of Geodesy, Vol. 73, No. 4, pp. 193-203, May 1999.
[https://doi.org/10.1007/s001900050236]

-
K. Draganová, P. Lipovský, and M. Šmelko, "IMU Accelerometer and Magnetometer Calibration Using Spectral Analysis", International Scientific Conference - New Trends in Aviation Development, Košice, Slovakia, pp. 41-45, Aug. 2018.
[https://doi.org/10.1109/NTAD.2018.8551682]

-
N. El-Sheimy, H. Hou, and X. Niu, "Analysis and Modeling of Inertial Sensors Using Allan Variance", IEEE Transactions on Instrumentation and Measurement, Vol. 57, No. 1, pp. 140-149, Jan. 2008.
[https://doi.org/10.1109/TIM.2007.908635]

-
I. M. Johnstone and B. W. Silverman, "Wavelet Threshold Estimators for Data with Correlated Noise", Journal of the Royal Statistical Society: Series B (Statistical Methodology), Vol. 59, No. 2, pp. 319-351, 1997.
[https://doi.org/10.1111/1467-9868.00071]

- VectorNav, "Inertial Navigation Primer", Vectronav Library, 2024.
-
Y.-H. Tu and C.-C. Peng, "An ARMA-Based Digital Twin for MEMS Gyroscope Drift Dynamics Modeling & Real-Time Compensation", IEEE Sensors Journal, Vol. 21, No. 3, pp. 2712-2724, Oct. 2021.
[https://doi.org/10.1109/JSEN.2020.3028140]

-
Y. Liu, J. Cui, and W. Liang, "Ahybrid learning-based stochastic noise eliminating method with attention-Conv-LSTM network for low-cost MEMS gyroscope", Front. Neurorobot., Vol. 16, Dec. 2022.
[https://doi.org/10.3389/fnbot.2022.993936]

-
S. Dutta and A. Pandey, "Overview of residual stress in MEMS structures: Its origin, measurement, and control", Journal of Materials Science: Materials in Electronics. Vol. 32. pp. 6705-6741, Mar. 2021.
[https://doi.org/10.1007/s10854-021-05405-8]

-
N. Gupta, et al., "Influence of residual stress on performance of AlN thin film based piezoelectric MEMS accelerometer structure", Microsyst Technol, Vol. 25, pp. 3959-3967, Feb. 2019.
[https://doi.org/10.1007/s00542-019-04334-1]

-
M. Hosseini-Pishrobat, D. Erkan, and E. Tatar, "Analytical and experimental study of stress effects in a MEMS ring gyroscope", Sensors and Actuators A: Physical, Vol. 362, pp. 114639, Nov. 2023
[https://doi.org/10.1016/j.sna.2023.114639]

-
Y. Zhang, H. Zhao, J. Ma, Y. Zhao, Y. Dong, and J. Ai, "A Deep Neural Network-Based Fault Detection Scheme for Aircraft IMU Sensors", International Journal of Aerospace Engineering, pp. 1-13, Sep. 2021.
[https://doi.org/10.1155/2021/3936826]

-
M. Crispoltoni, M. L. Fravolini, F. Balzano, S. D’Urso, and M. R. Napolitano, "Interval Fuzzy Model for Robust Aircraft IMU Sensors Fault Detection", Sensors, Vol. 18, No. 8, pp. 2488, Jul. 2018.
[https://doi.org/10.3390/s18082488]

-
G. Xiang, J. Miao, L. Cui, and X. Hu, "Intelligent Fault Diagnosis for Inertial Measurement Unit through Deep Residual Convolutional Neural Network and Short-Time Fourier Transform", Machines, Vol. 10, No. 10, pp. 851, Sep. 2022.
[https://doi.org/10.3390/machines10100851]

-
T. Gao, W. Sheng, M. Zhou, B. Fang, F. Luo, and J. Li, "Method for Fault Diagnosis of Temperature-Related MEMS Inertial Sensors by Combining Hilbert–Huang Transform and Deep Learning", Sensors, Vol. 20, No. 19, pp. 5633, Oct. 2020.
[https://doi.org/10.3390/s20195633]

-
V. Muthusamy and K. D. Kumar, "Failure Prognosis and Remaining Useful Life Prediction of Control Moment Gyroscopes Onboard Satellites", Advances in Space Research, Vol. 69, No. 1, pp. 718-726, Jan. 2022.
[https://doi.org/10.1016/j.asr.2021.09.016]

-
L. Tian and Z. Wu, "Degradation Modeling and Remaining Useful Life Prediction of Control Moment Gyroscope", Global Reliability and Prognostics and Health Management Conference (PHM-Hangzhou), Hangzhou, China, pp. 1-5, Oct. 2023.
[https://doi.org/10.1109/PHM-Hangzhou58797.2023.10482442]

- L. Grinsztajn, E. Oyallon, and G. Varoquaux, "Why do tree-based models still outperform deep learning on typical tabular data?", The 36th International Conference on Neural Information Processing Systems (NIPS), New Orleans LA USA, No. 37, pp. 507-520, Nov. 2022.
- A. Desai, C. Freeman, Z. Wang, and I. Beaver, "TimeVAE: A Variational Auto-Encoder for Multivariate Time Series Generation", arXiv preprint arXiv:2111.08095, , Nov. 2021.
- X. Yuan and Y. Qiao, "Diffusion-TS: Interpretable Diffusion for General Time Series Generation", The International Conference on Learning Representations (ICLR), Vienna Austria, pp. 1-29, Mar. 2024.
- F. Pedregosa, et al., "Scikit-learn: Machine learning in Python", Journal of Machine Learning Research, Vol. 12, pp. 2825-2830, Nov. 2011.
- I. Oguiza, "TSAI - A state-of-the-art deep learning library for time series forecasting, classification, and regression tasks", https://github.com/timeseriesAI/tsai, [accessed: Jan. 01, 2025]
- J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger, and A. G. Wilson, "GPyTorch: Blackbox matrix-matrix Gaussian process inference with GPU acceleration", The 32nd International Conference on Neural Information Processing Systems (NeurIPS), Montréal Canada, pp. 7587-7597, Dec. 2018.
-
G. R. Lee and J. P. Hespanha, "PyWavelets: A Python package for wavelet analysis", Journal of Open Source Software, Vol. 4, No. 36, Apr. 2019.
[https://doi.org/10.21105/joss.01237]

- tsai, "LSTMPlus", https://timeseriesai.github.io/tsai/models.rnnplus.html#lstmplus, [accessed: Jan. 01, 2025]
- tsai, "MultiInputNet", https://timeseriesai.github.io/tsai/models.multiinputnet.html, [accessed: Jan. 01, 2025]
- tsai, "MGRU_FCNPlus", https://timeseriesai.github.io/tsai/models.rnn_fcnplus.html#mgru_fcnplus, [accessed: Jan. 01, 2025]
- tsai, "TSTPlus", https://timeseriesai.github.io/tsai/models.tstplus.html, [accessed: Jan. 01, 2025]
- J. Hu, L. Shen, and G. Sun, "Squeeze-and-Excitation Networks", IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, pp. 7132-7141, Jun. 2018.

1995년 8월 : 연세대학교 전기전자공학과(공학석사)
2001년 2월 : 연세대학교 전기전자공학과(공학박사)
2002년 9월 ~ 현재 : 국립금오공과대학교 인공지능공학과, 컴퓨터공학과 교수
관심분야 : 딥러닝모델, 시계열분석, 스마트팩토리

2017년 3월 ~ 현재 : 국립금오공과대학교 수리빅데이터학과 학부과정
관심분야 : 머신러닝, 데이터분석

2021년 3월 ~ 현재 : 국립금오공과대학교 컴퓨터공학과 학부과정
관심분야 : 데이터분석, 딥러닝

2023년 3월 ~ 현재 : 국립금오공과대학교 인공지능공학과 학부과정
관심분야 : 데이터분석, 언어모델

2023년 3월 ~ 현재 : 국립금오공과대학교 컴퓨터공학과 학부과정
관심분야 : 생성모델