임피던스 경계 조건을 가진 SSPE 기법의 안정성 개선과 계산 가속화
초록
장거리 전자파 전파 모형화에 주로 사용되는 DMFT SSPE의 안정성을 개선하기 위해, 임피던스 경계 조건을 표현하는 미분 방정식에 대칭 차분을 도입하였다. 주어진 임피던스 경계 조건의 양끝점으로 일반해 계수를 도출함으로써, 고도 방향의 모든 표본을 합산하는 기존 기법을 단순화하였다. 진행 거리 방향에 대한 일반해 계수의 갱신 방정식을 새롭게 유도하여, 제안한 SSPE가 기존 방법에 비해 안정적으로 계산되도록 하였다. 본 연구에서 제시된 방법론은 기존 DMFT SSPE와 유사한 결과를 만들면서, 일반해 계수의 공식화가 기존에 비해 단순하며 효율적이다. 또한 DMFT를 FFT로 구현하는 수치 알고리즘을 제안하여 계산 속도를 높였다. DMFT와 대응하는 역변환을 FFT로 구현 가능한 이산 사인 및 코사인 변환으로 공식화하였다. FFTW와 cuFFT로 구현한 결과를 비교하면 cuFFT 기반 DMFT SSPE가 계산 시간 관점에서 2–3배 정도 빠르다.
Abstract
To improve the stability of Discrete Mixed Fourier Transform(DMFT) Split-Step Parabolic Equation(SSPE), commonly used for modeling long-range electromagnetic propagation, a symmetric difference scheme is introduced for the differential equations representing Impedance Boundary Conditions(IBCs). Utilizing the edge points of given IBCs to generate the coefficients of the general solution simplifies the conventional method, which requires summation of all samples along the height direction. By deducing new update equations for the coefficients of the general solution in the range direction, the proposed SSPE offers improved computational stability compared to the conventional method. The methodology presented in this work yields numerical results comparable to the conventional DMFT SSPE, while offering a simpler and more effective approach for the formulation of general solution coefficients. Additionally, a numerical algorithm is proposed that implements the DMFT using the FFT to accelerate computational speed. The DMFT and its corresponding inverse transform are formulated using discrete sine and cosine transforms, which can be implemented through the FFT. A comparison with results obtained using FFTW and cuFFT shows that the cuFFT-based DMFT SSPE is 2 to 3 times faster in terms of computation time.
Keywords:
electromagnetic propagation, parabolic equation, PE, difference equation, impedance boundary condition, DFT, FFTⅠ. 서 론
수치 해석 기법의 발전에 따라 맥스웰 방정식(Maxwell's equations)을 전체 공간에서 이산화해 수치 해석으로 다양한 안테나와 수동 소자의 복사 및 산란 결과를 얻고 있다. 하지만 장거리 범위에서 전자파의 전송 특성을 분석할 때는 포물형 방정식(PE, Parabolic Equation) 기법이 거의 유일한 방법론이다[1]. 왜냐하면 수십 km의 계산 범위로 인해 소요 메모리와 계산 시간이 많이 증가하며, 장거리 전송으로 인해 대기의 복잡한 굴절률 영향이 더해지기 때문이다. 따라서 PE 개념을 이용해 진행 거리를 큰 범위로 이산화할 수 있는 푸리에 변환(Fourier transform) 기반 알고리즘인 분할 단계 PE(SSPE, Split-Step PE)가 유용하다. 해수면이나 지표면은 이상적인 도체가 아니므로, 전기장과 자기장의 비율인 임피던스를 써서 높이 방향으로 푸리에 변환을 적용하는 이산 혼합 푸리에 변환(DMFT, Discrete Mixed Fourier Transform) SSPE도 많이 쓰인다[1][2]. SSPE는 많이 연구되어 왔기 때문에, 다양한 PE 방법론의 장단점에 대한 비교가 제시되어 있다[3]. 2차원 스칼라 파동(Scalar wave)을 쓰는 PE를 3차원 벡터로 확장하는 기법도 제안되었다[4]. DMFT SSPE를 써서 장거리 레이다의 탐지 오차를 보정하는 방식도 쓸모있다[5]. 최근에는 푸리에 변환 대신 웨이블릿 변환(Wavelet transform)을 PE에 적용하고 있다[6].
본 논문에서는 DMFT SSPE의 안정성을 개선하기 위해 경계면을 표현하는 미분 방정식을 대칭 차분으로 이산화한다. DMFT에 필수적인 일반해(General solution) 추가를 위해, 전체 표본의 합산(Summation) 대신 높이 방향 표본의 양끝점(Edge points) 혹은 표면점(Surface point)으로 미정 계수를 결정하는 기법을 제안한다. 일반해를 위한 미정 계수를 진행 거리(Range) 방향으로 갱신하는 방정식도 새롭게 유도해 제시한다. 또한 DMFT SSPE의 가속화를 위해 DMFT를 FFT의 표현식으로 변경하는 방식을 소개한다. FFT는 CPU용 FFTW[7]와 GPU용 cuFFT[8]를 선택한다. 본 연구를 바탕으로 해수면과 지표면의 매질 특성을 반영하고 장거리 범위의 연산 능력이 있는 DMFT SSPE의 안정성과 계산 속도를 개선한다. 여기에 더해 지형(Terrain)의 구조와 매질 종류까지 효과적으로 입력받아, 범용 및 특수 목적용 레이다 특성을 예측하는 SSPE 기반 M&S(Modeling and Simulation) 도구의 계산 엔진을 개발할 수 있다.
Ⅱ. SSPE의 안정성 개선
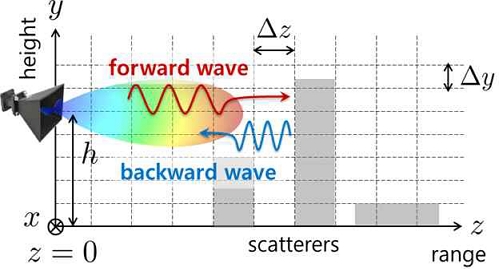
해수면 혹은 지표면을 따라 진행하는 전자파를 장거리에 걸쳐 분석할 때는 SSPE[1]를 주로 채택한다. SSPE 중에서 정확도가 높은 넓은 각 공식(Wide-angle formulation)을 그림 1의 좌표계를 기준으로 표현한다[1][3].
| (1) |
여기서 ym = mΔy, zs = sΔz, k0 = 2π/λ0; 안테나는 z = 0과 y = h에 놓이며, pk는 높이인 y방향으로 푸리에 변환한 연속 파수(Continuous wavenumber) p의 k번째 이산 파수(Discrete wavenumber), F[⋅]와 F-1[⋅]는 경계 조건을 고려한 푸리에 변환 및 역변환, 계산 표본의 색인(Index)은 m = 0,1,⋯,M-1, s = 0,1,⋯,L-1 범위에서 변하며, neff는 대기 특성과 지구 곡률을 반영한 유효 굴절률(effective refractive index)[1]이다. 식 (1)에 등장하는 u(z,y)는 표본 위치 (z,y)에서 계산한 정규화 장(Normalized field)이다. 수평 편파(HP, Horizontal Polarization)와 수직 편파(VP, Vertical Polarization)에 따라 u(z,y)는 각각 전기장 및 자기장에 연결된다.
| (2: HP) |
| (3: VP) |
여기서 HP와 VP는 지표면에 대해 전기장이 향하는 방향으로 정한다.
해수면이나 지표면에 대한 이상적인 모형화를 위해서는 해양이나 지각 전체에 대한 유전율 분포를 포함한 SSPE를 사용해야 한다. 하지만 현실적으로 계산 메모리와 시간에 한계가 존재하므로, 구조의 표면에 해당하는 해수면과 지표면을 임피던스 경계 조건(IBC, Impedance Boundary Condition)으로 근사해서 SSPE를 처리한다. 임의의 3차원 영역을 경계 임피던스(Boundary impedance)를 가진 2차원 표면으로 바꾸는 IBC[9]는 전자파의 입사각 영향을 받는 근사 기법이지만 표면 계산만으로 영역의 반사 특성을 얻는 효율적인 방법이다. IBC를 고려해 식 (1)에 나온 푸리에 변환을 이산적으로 변형한 기법은 DMFT SSPE가 된다[1]. 푸리에 변환을 차분한 DMFT는 전방 차분(Forward difference), 후방 차분(Backward difference), 중앙 차분(Central difference) 등으로 구현할 수 있다. 수치 미분 관점에서 정밀도가 높은 방식은 중앙 차분 Δc이지만[2, 식 (16)], 표본 색인 위치에서 1/2인 지점을 원래값으로 추정하므로, 이용하려는 표본값에 오차가 존재한다. 이를 극복하기 위해 DMFT에 대칭 차분(Symmetric difference) Δs를 도입한다.
| (4: 중앙 차분) |
| (5: 대칭 차분) |
여기서 fm은 m번 위치의 표본값이다. 중앙 차분과 다르게 대칭 차분은 표본 위치의 함수값을 그대로 사용하기 때문에 중앙 차분에 비해 정확도가 높아진다. 중앙 차분으로 만든 DMFT를 바꾸어서 대칭 차분 Δs를 활용한 DMFT를 제안한다.
| (6) |
여기서 pk = kπ/ymax, ymax = (M-1)Δy; α는 편파에 따라 IBC에서 접선과 법선 경계 조건을 섞어주는 혼합 계수(Mixed coefficient)이다. 식 (6)의 급수 안에 담긴 항은 IBC를 표현하는 미분 방정식의 이산화이며, 급수는 이산 사인 변환(DST, Discrete Sine Transform)의 모양을 가진다. 식 (6)에 식 (5)를 대입하고 간략화를 위해 M을 짝수라 가정한다.
| (7) |
여기서 , tanc(x) = tanx/x; Σ'은 이산 코사인 변환(DCT, Discrete Cosine Transform)에 주로 사용되는 으뜸 합산(Prime summation) 기호[2]이다. 으뜸 합산은 양끝점인 m = 0과 M-1인 항에 가중치 1/2을 곱해 더하며 나머지 항은 원래 Σ 연산으로 합한다. 그림 1에서 높이 방향의 간격 Δy를 매우 작게 줄이면, 식 (7)은 통상적인 DMFT[2]로 환원된다.
| (8) |
여기서 , tanc(x) ≈ 1, tan(x) ≈ 0이다. 따라서 식 (6) 혹은 (7)은 기존 DMFT에 수렴하는 효율적인 대체 관계식이 된다. 왜냐하면 식 (8)은 DCT와 DST로 처리하지만, 식 (6)은 DST만으로 계산 가능하기 때문이다. DMFT는 역변환(IDMFT, Inverse DMFT)에 결함이 있어서 차분 방정식(Difference equation)의 일반해(General solution)로 보정을 해야만 원래 함수 fm을 오차없이 얻을 수 있다[1]. 이에 따라 식 (6)의 역변환 IDMFT를 다음처럼 공식화한다.
| (9) |
여기서 fm,p 및 fm,g는 fm용 차분 방정식의 특수해(Particular solution) 및 일반해; Sa(x) = sinx/x,
| (10) |
| (11) |
| (12) |
상수 c1,c2는 IBC로 정하는 차분 방정식의 계수이다. 기존 DMFT에서는 기저 함수의 직교성을 적용해서 표본 fm의 전체 합(Summation)으로 c1,c2를 결정한다[1].
| (13) |
| (14) |
반면에 IBC의 양끝점(Edge points)인 m = 0과 M-1에서 함수값은 0이라는 조건과 식 (10)을 사용해서 식 (13)을 단순화할 수 있다.
| (15) |
또한 M을 충분히 키우면 가장 높은 고도인 y = ymax에 있는 함수값 fM-1의 크기는 매우 작아진다. 그래서 m = 0의 표면점(Surface point)만 포함하도록 식 (15)를 더욱 간략화한다.
| (16) |
수렴하는 급수인 식 (10)에 m = 0을 대입해서 f0,p만 정하므로, rm의 고차 항까지 합산하는 식 (13)에 비해 식 (15)는 안정적으로 c1,c2를 연산할 수 있다. 여기서 Fk는 식 (1)과 같은 SSPE 절차에서 이미 주어져 있다. SSPE의 다음 단계에서도 c1,c2가 필요해서, 이전 zs에서 얻은 c1,c2로 다음 zs+1 위치의 c1,c2도 다음과 같은 갱신 방정식(Update equation)으로 새롭게 추정한다.
| (17) |
여기서 제곱근 함수 는 복소 영역에서 다가성(Multi-valuedness)을 가지므로 수렴성을 위해 제곱근의 허수부가 항상 양수가 되도록 제곱근의 부호를 뽑는다.
Ⅲ. SSPE의 계산 가속화
SSPE의 계산 속도를 높이려면 이산 푸리에 변환(DFT, Discrete Fourier Transform)을 빠르게 처리하는 고속 푸리에 변환(FFT, Fast Fourier Transform)이 필수적이다. 많이 사용되는 FFT 패키지로 FFTW[7]와 cuFFT[8]가 있다. FFTW는 CPU, cuFFT는 CUDA (Compute Unified Device Architecture) 기반으로 GPU[10]에서 실행된다. 그렇지만 FFTW와 cuFFT는 DMFT를 지원하지 않기 때문에, FFT를 바탕으로 새롭게 DMFT를 구현해야 고속으로 푸리에 변환과 역변환을 계산할 수 있다. 이 개념을 바탕으로 식 (6)과 (10)을 DST와 DCT로 표현한다.
| (18) |
| (19) |
여기서 DST[⋅]과 DCT[⋅]는 각각 이산 사인 및 코사인 변환이다. 다음 단계로 DST와 DCT를 FFT로 연결한다.
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
여기서 FFT는 FFTW나 cuFFT를 이용, trunc[⋅]는 sym[⋅]과 asym[⋅] 연산자로 증가시킨 벡터 차원을 다시 원래 크기로 자르는 절단자(Truncator), rem(m,M)은 m을 M으로 나눈 나머지(Remainder), ⌊x⌋는 바닥 함수(Floor function)이다.
Ⅳ. 수치 계산 및 검증
식 (1)에 필요한 푸리에 변환 F[⋅]와 역변환 F-1[⋅]을 식 (6)과 (9)에 정의한 DMFT와 IDMFT로 각각 치환하여 SSPE를 처리한다. 이때 고속 연산을 위해 CPU와 GPU의 FFT 알고리즘을 포함한 식 (18)과 (19)로 빠르게 계산한다.
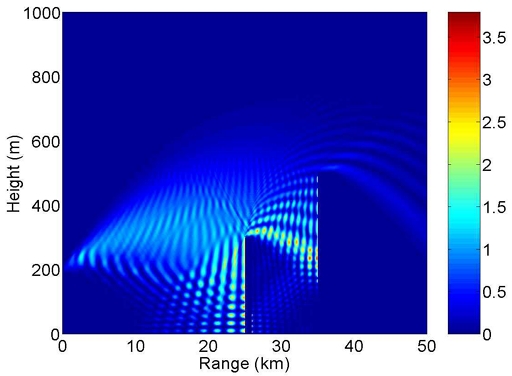
그림 1과 같은 SSPE 좌표계에서 안테나가 수평 편파(HP, Horizontal Polarization)로 전방파(Forward wave)를 복사할 때 장애물에 의해 발생하는 산란(scattering)을 표현하는 정규화 장 u(z,y)의 크기 분포를 그림 2에 가시적으로 보인다. 안테나의 빔폭(Beamwidth) θbw는 1°, 주빔(Main beam) 각도 θm도 표면 기준으로 1°에 둔다. 장애물은 z = 25 km에서 길이 1 km 및 높이 300 m로 배치되며, 추가적으로 길이 2 km 및 높이 500 m를 가진 장애물이 z = 35 km에도 존재한다. 여기서 장애물의 구성 물질은 석회석(ϵr = 7.5, σ = 0.03 S/m)을 가정한다. 지면 y = 0의 경계 조건은 땅바닥(ϵr = 30, σ = 0.02 S/m)으로 설정한다. HP에 대한 혼합 계수 αh는 프레넬 방정식(Fresnel equation)으로 설정한다.
| (24) |
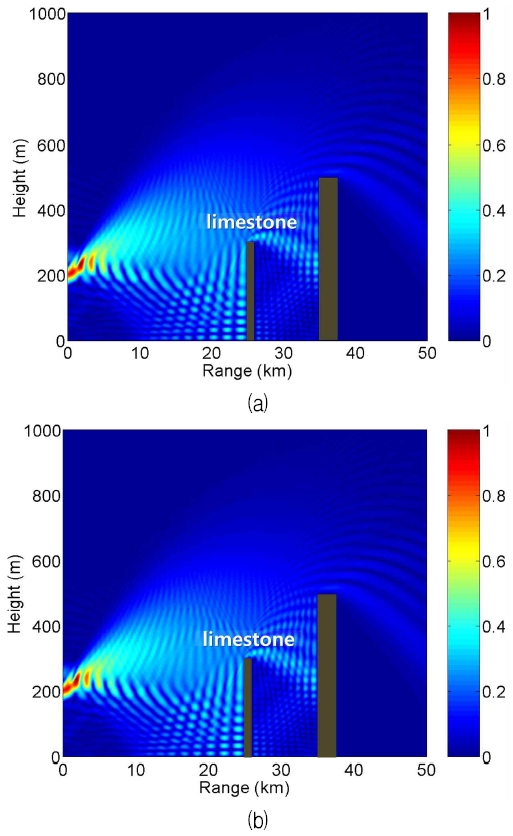
Magnitude distributions of normalized field u(z,y) computed using DMFT SSPE for horizontal polarization (a) Conventional DMFT (b) Simplified DMFT by Eqn. (16)
여기서 ϵrc는 표면의 복소 유전 상수(complex dielectric constant), 는 복소 굴절률(Complex refractive index)이다. DFT의 성질로 인해 y = ymax에도 y = 0과 동일한 경계 조건이 부여된다. 이에 따라 최고 고도에서 불필요한 반사가 생기므로, y > ymax를 벗어난 영역에 완충(Buffer)과 필터(Filter) 영역을 두어서[1] 전자기장이 높이에 따라 감쇠하도록 한다. 그림 2의 계산에는 한 창 함수(Hann window function)를 써서 감쇠 필터를 구현한다. 대기의 유효 굴절률은 제곱근 함수로 근사한다[1].
| (25) |
여기서 a0은 대기층 도관 현상(Ducting)을 조절하는 굴절률 매개변수이다. 식 (25)에 의해 높이 y가 올라갈수록 굴절률이 작아지기 때문에, 장거리로 전자파가 전파될 때 파동은 지면 방향으로 휘어진다. 장애물에 의한 전자파 반사를 고려하려고 그림 1에 표시한 후방파(Backward wave)도 추가한다. SSPE 과정에서 전방파와 후방파를 차례로 계산하는 반복수는 D로 표기한다. 그림 2는 양방향(2-way) 계산 회수를 D = 3로 설정해 반복 합산한 최종 결과를 보여준다. 반복 회수 D를 3보다 더 높여도 그림 2와 거의 비슷한 분포가 나온다. 그림 3은 그림 2와 동일한 조건에서 수직 편파(VP, Vertical Polarization)로 얻은 u(z,y)의 크기 분포를 보여준다. VP의 혼합 계수 αv는 식 (24)에서 변형된다.
전체적인 특성은 HP와 비슷하지만, 전기장과 자기장의 반사도 특성이 반영되어 석회석 산란체 가까이에서는 분포가 서로 다르다.
| (26) |
그림 3에 보인 정규화 장의 크기 분포로 전자파의 장거리 전파 특성을 예측할 때는 전파 인자(PF, Propagation Factor)를 활용한다[1][11]. PF의 정의에 식 (2) 혹은 (3)을 대입해 공식을 만든다.
| (27) |
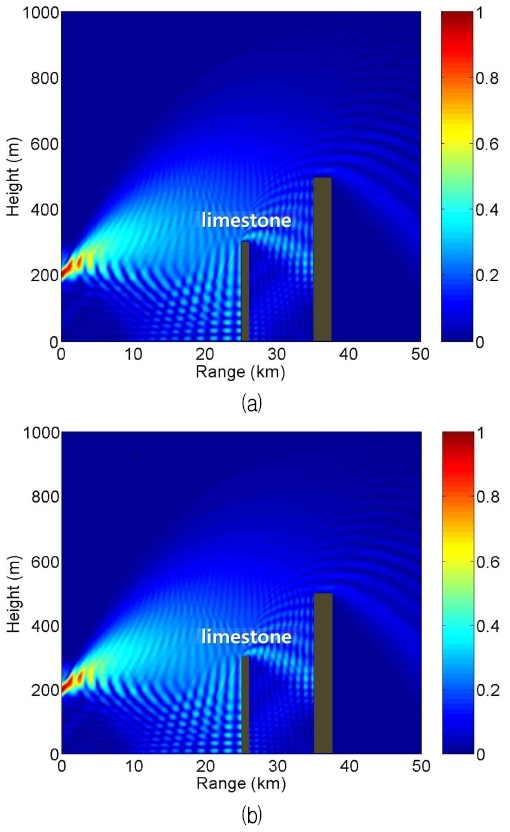
Magnitude distributions of normalized field u(z,y) computed using DMFT SSPE for vertical polarization (a) Conventional DMFT (b) Simplified DMFT by Eqn. (16)
여기서 ; neff ≈1로 가정, Pr은 (zr,yr)에서 계산한 수신 전력, P0은 PF의 기준 전력이다. 그림 4를 보면 입사파와 반사파가 공존하는 산란체 근방에서 PF는 다소 크게 나온다. 특히 첫째와 둘째 장애물 사이에는 식 (24)의 a0에 의한 도관 현상이 관찰된다. 전체 계산 영역에서 전파 인자의 최대값은 max(PF) = 3.79 = 5.79 dB이다. 그림 4에서 높이를 y = 200 m로 고정하고 진행 거리 z에 대한 PF의 특성을 분석한 결과는 그림 5에 있다. PF를 계산할 때 DMFT의 계수 c1,c2는 식 (13), (15), (16)으로 얻으며, 그 결과들은 그림 5에 각각 summation, edge points, surface point로 표기한다. 세 가지 결과는 PF 관점에서 거의 비슷하다.
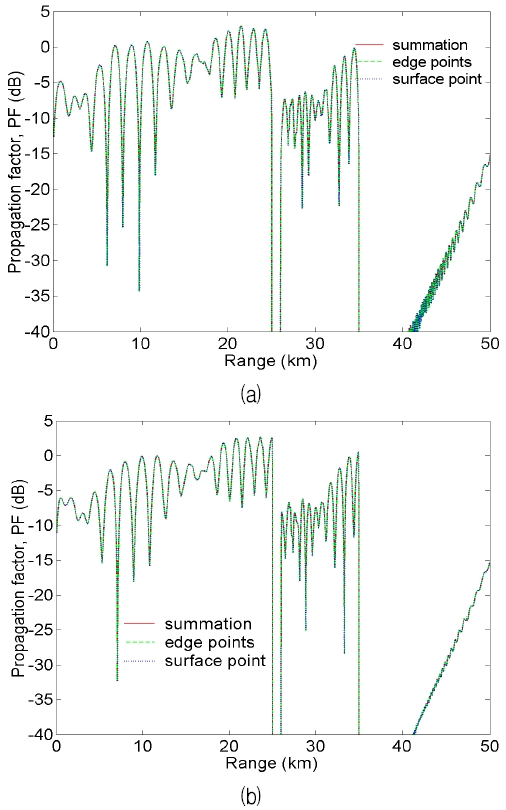
Variations of propagation factor versus range for DMFT constants c1,c2 at height y = 200 m (a) Horizontal polarization (b) Vertical polarization
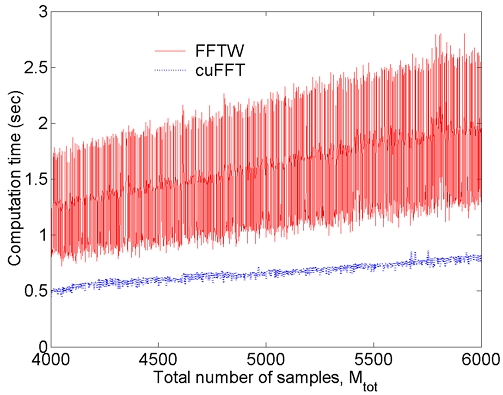
그림 6은 식 (18)–(21)로 공식화한 FFTW와 cuFFT로 구현한 DMFT SSPE의 계산 속도 특성을 보여준다. FFT 속도를 비교하기 위해, 그림 3의 조건과 다르게 진행 거리를 zmax = 10 km로 제한하고 D = 1로 둔 단방향(1-way) 계산만 한다. SSPE에 쓰는 y방향의 전체 표본수는 Mtot = M+Mb+Mf이다. 여기서 Mtot는 M외에 감쇠 필터를 만드는 완충 영역 개수 Mb와 필터 영역 개수 Mf를 포함한다. SSPE의 단순화를 위해 Mb = Mf로 둔다. FFTW와 cuFFT 처리에는 각각 3.7GHz의 10개 코어와 128GB RAM을 가진 CPU 및 5,888개 코어와 8GB RAM을 쓰는 GPU를 사용한다. 선택한 모든 Mtot에 대해 cuFFT가 FFTW 대비 2–3배 정도 빠른 계산 속도를 보여준다. 또한 FFTW는 Mtot에 대한 속도 변동성이 2배 정도 존재하지만, cuFFT의 계산 시간은 Mtot에 비례하여 조금 증가한다. 그래서 FFTW를 쓰려면 계산 시간이 짧은 Mb 혹은 Mf를 선택하여야 한다.
Ⅴ. 결 론
대기 굴절률을 고려한 전자파의 장거리 전송 특성을 분석하는 DMFT SSPE의 안정성을 개선하기 위해 대칭 차분을 도입하고 DMFT의 일반해 계수를 양끝점만으로 계산한다.
계산 고도를 충분히 높인 경우, 일반해 계수를 양끝점 대신 표면점에서만 얻어도 기존 DMFT와 동일한 결과를 얻을 수 있다. 또한 DMFT SSPE의 계산을 가속하려고 FFTW와 cuFFT로 DMFT와 그 역변환을 구현한다. 높이 방향으로 표본수를 변화시키면서 계산한 시간을 비교하면, FFTW에 비해 cuFFT가 모든 경우에서 2–3배 정도 우수하다. 본 연구를 바탕으로 표면 매질의 종류와 계산 고도 및 진행 거리에 대한 수렴 특성을 분석하여, DMFT SSPE를 더욱 현실적인 전파 분석 알고리즘으로 발전시킬 예정이다.
Acknowledgments
본 연구는 2024년 국방과학연구소의 지원(과제 번호: UI220077JD)을 받아 수행되었습니다
References
-
G. Apaydin and L. Sevgi, "Radio Wave Propagation and Parabolic Equation Modeling", Hoboken, NJ, USA: John Wiley & Sons, pp. 53-64, Aug. 2017.
[https://doi.org/10.1002/9781119432166]

-
J. R. Kuttler and R. Janaswamy, "Improved Fourier transform methods for solving the parabolic wave equation", Radio Science, Vol. 37, No. 2, pp. 5-1–5-11, Apr. 2002.
[https://doi.org/10.1029/2001RS002488]

-
P. Zhang, L. Bai, Z. Wu, and L. Guo, "Applying the parabolic equation to tropospheric groundwave propagation: A review of recent achievements and significant milestones", IEEE Antennas and Propagation Magazine, Vol. 58, No. 3, pp. 31-44, Jun. 2016.
[https://doi.org/10.1109/MAP.2016.2541620]

-
X. Zhang and C. D. Sarris, "Statistical modeling of electromagnetic wave propagation in tunnels with rough walls using the vector parabolic equation method", IEEE Transactions on Antennas and Propagation, Vol. 67, No. 4, pp. 2645-2654, Apr. 2019.
[https://doi.org/10.1109/TAP.2019.2894285]

-
J. Heo, J. Yang, J. Kim, D.-Y. Na, and Y. B. Park, "Propagation analysis using discrete mixed Fourier transform-based parabolic equation method for long range radar detection error correction", IEEE Access, Vol. 11, pp. 119436-119445, Oct. 2023.
[https://doi.org/10.1109/ACCESS.2023.3327429]

-
A. Rocha, D. Parada, D. Tami, D. Guevara, and C. G. Rego, "An efficient and accurate algorithm for electromagnetic wave propagation modeling based on wavelet transforms", Journal of Microwaves, Optoelectronics and Electromagnetic Applications, Vol. 23, No. 1, Mar. 2024.
[https://doi.org/10.1590/2179-10742024v23i1279458]

- M. Frigo and S. G. Johnson, "C Subroutine Library for Computing the DFT", FFTW 3.3.10, 2022.
- "cuFFT Library User's Guide: cuFFT API Reference", NVIDIA Corp., California, USA, pp. 25-36, 2022.
-
J.-H. Nam and I.-S. Koh, "Implementation of zero-thickness impedance boundary condition for method of moments and application to microstrip antennas", Journal of Electromagnetic Engineering and Science, Vol. 22, No. 3, pp. 386-388, May 2022.
[https://doi.org/10.26866/jees.2022.3.l.4]

-
Y.-J. Choi and I.-S. Choi, "Dynamic RCS calculation of wind turbine blade using GPU-based TSM-RT", The Journal of Korean Institute of Electromagnetic Engineering and Science, Vol. 31, No. 3, pp 245-252, Mar. 2020.
[https://doi.org/10.5515/KJKIEES.2020.31.3.245]

-
K.-S. Kim, J.-H. Youn, H.-G. Yang, Y.-S. Chung, W.-W. Lee, and K.-B. Bae, "M&S tool for analyzing the detection performance in bistatic radar", The Journal of Korean Institute of Electromagnetic Engineering and Science, Vol. 22, No. 6, pp 631-640, Jun. 2011.
[https://doi.org/10.5515/KJKIEES.2011.22.6.631]


1998년 2월 : 경북대학교 전자공학과(공학사)
2000년 2월 : KAIST 전자전산학과(공학석사)
2002년 8월 : KAIST 전자전산학과(공학박사)
2002년 9월 ~ 2003년 2월 : 한국전자통신연구원 선임연구원
2003년 3월 ~ 현재 : 목원대학교 게임SW공학과 교수
관심분야 : 수치 해석, 광선 추적, 병렬 처리

1988년 2월 : 경북대학교 전자공학과(공학사)
1990년 2월 : 경북대학교 전자공학과(공학석사)
1990년 3월 ~ 현재 : 국방과학연구소 수석연구원
관심분야 : Radar target signature prediction and measurement, platfom RCS reduction, synthetic aperture radar target recognition, aircraft & ship susceptibility modeling & simulation