다채널 DenseNet을 이용한 뇌 MRI의 QQ 기반 OEF 예측 방법

Ⅰ. 서 론

현대 사회에서 뇌와 관련된 질환은 다양한 형태로 나타나고, 높은 사망률을 기록하는 주목받는 질환 중 하나이다[1]. 이러한 질환을 진단하고 치료하기 위해서는 질환의 원인을 빠르게 파악하고 조치하는 것이 중요하다[2]. 이를 위해서 뇌 조직의 활성화 상태를 분석하여 뇌의 상태를 파악하는 방법이 있으며, 이 과정에서 컴퓨터 단층촬영 기법, 자기공명영상(MRI, Magnetic Resonance Imaging) 기법 등의 다양한 기술이 활용되고 있다. 특히 MRI는 비침습적으로 뇌의 구조 및 기능 상태를 상세하게 확인할 수 있어서 뇌 이상 탐지에 널리 사용된다.

뇌 MRI를 이용하여 뇌 관련 질환을 진단하기 위해서는 뇌 조직에서 혈액 내 산소 소모량을 파악할 필요가 있다. 이는 뇌 조직에서 산소추출률(OEF, Oxygen Extraction Fraction)을 계산하여 파악할 수 있고, OEF는 뇌의 활동을 반영하는 중요한 지표로 뇌 질환의 조기 진단에 활용되기 때문에 정확한 측정을 위한 기술이 필요하다[3].

이를 위해 다양한 OEF 측정 연구들이 진행되었고, Turbo QUIXOTIC[4], 15O-O2 단시간 흡입을 이용한 PET[5], qBOLD(quantitative Blood Oxygenation Level Dependent) 모델[6], QQ 모델[7]과 같은 방법들이 제안되었다. 각각 모델들은 다양한 제약사항들을 가지고 있으나 QQ 모델은 제약사항이 가장 느슨하며, QSM(Quantitative Susceptibility Mapping)과 qBOLD를 결합한 모델로 MRI 데이터에서 얻어진 정보를 기반으로 더 나은 OEF 예측 성능을 제공한다. 최근 연구들에서도 QQ 모델을 활용한 연구 및 딥러닝 모델을 활용하는 연구가 지속적으로 진행되고 있다[8]-[12].

뇌 MRI 데이터를 활용한 QQ 모델을 기반으로 OEF 예측의 정확도를 향상하기 위해 본 논문에서는 다채널 DenseNet 모델을 이용한 QQ 모델의 파라미터 추정과 OEF 예측하는 방법을 제안한다. QQ 모델의 파라미터는 정맥 산소포화도 Y, 정맥 혈액량 v, 조직의 가로 이완 R2, 에코 타임 0에서의 신호 강도 S0, 비혈류 물질의 자화율 χnb가 있다. 각 파라미터 중 Y 값을 통해 OEF 예측이 수행되기에 파라미터에 대한 정확한 예측이 필요하다. 기존 방법들과 다르게 QQ 모델의 각 입력 채널에 대하여 DenseNet 모델을 적용하였고 이를 통합하여 최종 출력을 계산한다. 각 DenseNet 모델은 하나의 입력 계층, 네 개의 밀집 블록과 세 개의 Transition 계층, 하나의 출력 계층으로 구성되어 있으며 1차원 데이터를 다루기 위해 1D 컨볼루션 계층을 사용하였다. 제안한 모델은 17명 환자의 MRI 데이터를 사용하여 학습 및 검증을 진행하였다.

본 논문은 다음과 같이 구성되어 있다. 2장에서 관련 연구를 요약하고, 3장에서는 제안하는 다채널 DenseNet 모델 기반 방법에 대해서 설명한다. 4장에서는 실험 결과 및 분석을 제시하고, 5장에서 결론과 향후 연구 과제에 대해 논의한다.

Ⅱ. 관련 연구

뇌의 질환을 판단하는 데에 있어 각 조직에서 산소 소모량은 중요한 역할을 한다. 이를 위해 MRI를 통해 OEF 계산을 위한 다양한 연구들이 진행되고 있다. QUIXOTIC, qBOLD 등 모델이 제시되었으나 OEF 계산에 특정한 가정이 요구된다. QUIXOTIC은 VSSL(Velocity-Selective Spin Labeling)을 사용하여 PCV(Postcapillary Venular) 혈액 신호를 분리할 수 있다고 가정한 후 이를 통해 순수 혈액 신호를 얻을 수 있다고 가정한다. qBOLD는 혈액의 산소 포화도 변화를 통해 OEF를 계산한다. 이때 혈류와 대사 상태를 가정하고, 일정한 생리학적 상태를 가정한다. 이러한 가정 때문에 두 모델은 가정이 다른 경우 올바른 계산 결과를 얻기 어렵다[7]-[9].

QSM은 조직 내 자기 감수성 변화를 측정하여 뇌 조직의 철분 농도나 혈류 동역학을 평가하는 데 사용되며, qBOLD는 혈액의 산소 포화도 변화를 통해 뇌의 대사 상태를 평가한다. QQ 모델은 QSM과 qBOLD를 결합함으로써 각 방법이 갖는 제약사항을 상호 보완하였고, 특정한 가정을 하지 않고도 OEF를 효율적으로 계산할 수 있다. 그러나 자기 감수도 변화에 민감한 QSM과 혈액 산소 포화도 변화에 민감한 qBOLD를 결합하는 과정에서 QQ 모델도 잡음에 의한 영향이 커질 수 있다. 특히, MRI 데이터가 내재하고 있는 잡음에 대하여 QQ 모델이 민감하여 정확한 OEF 계산에 어려움이 있다[7]-[9].

이와 같은 잡음에 대한 민감성을 개선하기 위해 시간에 따른 MRI 데이터 변화를 분석하고 잡음 영향을 감소시키는 CAT(Cluster Analysis of Time evolution) 방법[8]과 클러스터링을 통하여 잡음에 대한 영향을 줄이는 CCM(Cluster-based Classification and Matching) 방법[9]도 연구되었다. 최근에는 QQ 모델에 대하여 딥러닝 모델들과 결합하여 기존 방법보다 간단하게 OEF를 계산하기 위한 연구들이 진행되고 있다[11][12].

Ⅲ. 다채널 DenseNet 모델을 이용한 QQ 기반 OEF 예측 방법

본 절에서는 뇌 MRI에 기반하는 QQ 모델에 대하여 다채널 DenseNet 모델을 사용해서 파라미터를 추정하고 OEF를 예측하는 방법에 대해 제안한다.

3.1 DenseNet 모델 및 구조 설계

DenseNet은 주로 이미지 처리 분야에서 우수한 성능을 보이는 딥러닝 모델 중 하나이다. 기본적으로 CNN(Convolutional Neural Network)의 한 종류로 합성곱 계층을 기반으로 하지만 특별한 형태의 네트워크 구조를 통해 CNN에서의 제약이 해소되는 다소 다른 특징들을 가지고 있다.

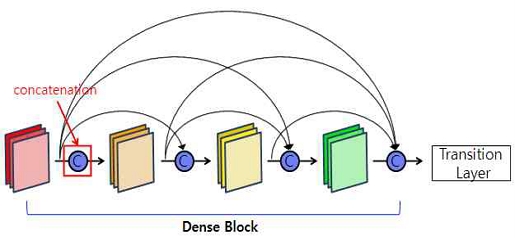
DenseNet의 주요 특징 중 하나인 밀집 연결 구조에 대해 그림 1에 나타내었다. Dense Block 내의 각 계층이 이전 모든 계층의 출력을 입력으로 받는 밀집 연결 구조는 정보의 흐름을 최대화하고 기울기 소실 문제를 완화하여 줌으로써 특징 재사용을 촉진하여 준다. 각 Dense Block은 Batch Normalization, Activation, Convolution으로 구성되며 이전 계층의 출력과 현재 계층에 대한 Concatenate 연산을 통해 특징을 결합한다. 또한, 밀집 연결로 인해 입력 특징맵 수가 증가할 수 있으나 Growth Rate를 통해 특징맵의 채널 수를 조절하고, 특징 재사용을 통해 파라미터를 공유하여 모델의 크기와 메모리 사용량을 감소시켜 모델 성능을 향상시킨다.

Fig. 1.

Structure of dense block

Dense Block 이후 Transition 계층을 통해 특징맵의 크기를 감소시키고 모델의 깊이를 조정한다. 이러한 Dense Block과 Transition 계층의 반복으로 DenseNet을 구성하여 특징 재사용, 효율적인 파라미터 사용, 기울기 소실 완화 등의 장점이 있다.

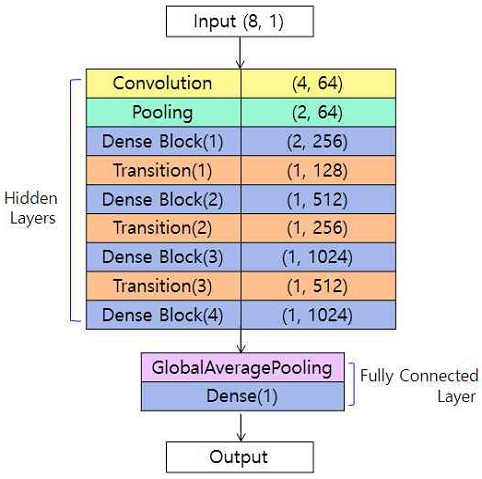
그림 2에 본 논문에서 각 채널에 적용하기 위해서 설계한 DenseNet 모델의 구조를 나타내었다. 이 모델은 총 8개의 입력값에 대응하는 입력 계층 1개와 Dense Block 4개, 차원 감소를 위한 Transition 계층 3개, QQ 모델의 각 파라미터에 대응되는 1개 노드의 출력 계층으로 구성하여 깊이를 증가시키고 특징 추출 능력을 강화하였다. 입력 계층은 8개의 노드를 가지고, 각 노드는 뇌 MRI 데이터의 특정한 특징을 나타낸다. Dense Block이 입력 데이터를 받아 특징을 추출하고, 이를 통해 각각의 QQ 모델 파라미터에 대응되는 출력을 생성한다. 출력 계층은 QQ 모델의 파라미터에 대해 적절히 특징을 학습할 수 있도록 하고 이를 통해 OEF 예측을 수행한다.

Fig. 2.

Structure of 1 channel DenseNet model

해당 모델은 DenseNet 121 모델과 유사한 구조를 가지도록 설계하였다. 각 Dense Block은 이전 층의 출력을 입력으로 받아들이며, Bottleneck 구조를 6번 반복한다. 초기에는 6회 반복으로 시작하며, 이후에는 각 Dense Block에서 두 배씩 증가하는 계층을 포함하도록 설계하였다.

Transition 계층은 Dense Block 이후에 위치시켜 모델의 복잡도를 줄이고 연산량을 감소시켜 과적합을 방지하였다. 이를 통해 블록 간의 채널 수를 조절하고 공간 차원을 감소시키도록 하였다. 또한, 모델의 마지막 부분에 Global Average Pooling Layer를 배치하여 공간 정보를 감소시키도록 하였다.

이러한 모델 구조를 통해 모델의 학습 및 성능을 향상시키고 효과적인 특성 추출이 가능하도록 하였으며 DenseNet 121과 유사한 구조를 적용함으로써 이전에 검증된 딥러닝 아키텍처를 활용하여 모델의 성능을 향상시켰다.

3.2 다채널 DenseNet 모델을 이용한 QQ 기반 OEF 예측 모델

제안하는 다채널 DenseNet 모델에서는 QQ 모델 파라미터 추정의 정확도 개선을 위해 각 파라미터에 대해 1개의 출력 노드로 결과가 출력되도록 개별 DenseNet 모델을 수립한 후에 개별 학습을 진행하도록 구성하였다.

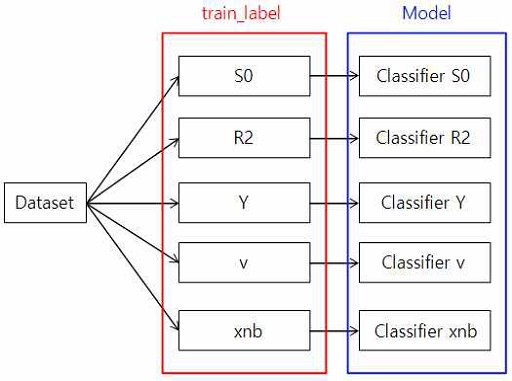
그림 3에는 이와 같은 방법에 대하여 특정 라벨별로 학습을 진행할 수 있도록 학습 데이터에 대한 라벨을 분할하여 모델 학습을 진행하는 모습을 도식화하였다. 다양한 특징과 관련 라벨들이 포함된 데이터셋에 대해 특정 라벨에 대한 학습 및 예측이 가능하도록 S0, R2, Y, v, χnb에 대한 데이터를 포함하는 train_label을 생성한다. 이후 학습하고자 하는 라벨을 train_label에서 선택하여 해당 데이터에 대한 학습을 수행한다. 이를 통해 원하는 라벨에 대한 특징을 적절하게 학습한 모델을 생성하여 정확도를 개선하였다.

Fig. 3.

Individual learning of each DenseNet by label

이와 같은 다채널 학습 방식을 통해 각 라벨에 대해 독립적으로 최적화된 모델을 생성하여 전체적인 성능을 향상시킨다.

제안하는 모델에서 각 DenseNet의 학습 파라미터로 학습률은 적절한 학습 속도 유지를 위해 1e-4로 설정하였고, 손실 함수는 큰 차이가 나는 값에 주목하기 위해 평균 제곱근 오차(Root Mean Square Error, RMSE), 최적화 함수는 Huber를 사용하였다. 학습은 메모리 효율 및 학습 속도를 고려하여 512 배치 사이즈로 설정하여 최대 100 에포크로 진행하였다. 또한, 모델의 과적합 방지 및 학습 시간 관리를 위해 학습 과정에서 7회까지 검증 데이터의 손실 값이 개선되지 않으면 학습을 종료하도록 조기 멈춤을 설정하였다.

Ⅳ. 실험 결과 및 성능 분석

제안하는 방법은 Intel i9-11900(8C 16T) CPU 및 64GB RAM, NVIDIA RTX 3090 GPU 하드웨어 및 Windows 10 Pro 운영체제 환경에서 개발 및 RMSE 정확도 분석을 수행하였다. 또한 다채널 DenseNet 모델의 구현은 Tensorflow의 Keras를 이용하였다.

4.1 학습과 검증 정확도

제안하는 방법의 학습 및 검증은 코넬대학교 의과대학에서 구축한 데이터셋을 사용하여 진행하였다. 해당 데이터셋은 17명의 환자로부터 얻은 뇌 MRI 신호 값과 자화율 데이터 정보가 포함된 4차원 데이터(3차원 데이터 + 측정시간)로 구성되어 있다. 또한 모델의 출력으로 사용된 QQ 모델의 파라미터 값인 정맥 산소포화도 Y, 정맥 혈액량 v, 조직의 가로 이완 R2, 에코 타임 0에서의 신호 강도 S0, 비혈류 물질의 자화율 χnb에 대한 값이 포함되어 있다[8][9]. 각 3차원 데이터는 스캔 파라미터 설정에 따라서 512x512x70, 512x512x46, 512x512x66, 512x512x60 등 크기로 구성되어 있고, 이 중에서 뇌영역에 해당하는 총 30,679,201개 샘플을 제안하는 모델의 입력으로 사용하기 위해 1차원으로 변형한 후에 학습, 검증, 평가 데이터로 분할하여 사용하였다. 17명의 환자 데이터 중 6명의 환자 데이터(P1, P2, P10, P14, P15, P17)을 학습 및 검증에 8 : 2 비율로 분할하여 사용하였다. 그 외 11명의 환자 데이터를 제안하는 방법의 평가에 사용하였다.

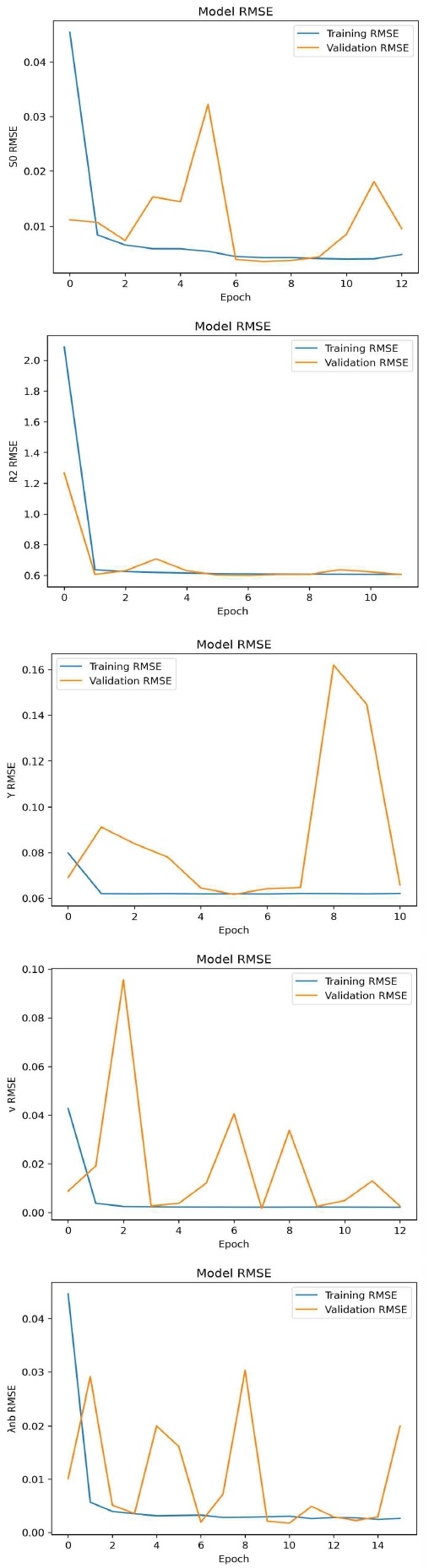
그림 4에 학습 및 검증 데이터를 사용한 다채널 DenseNet의 훈련 과정에서 각 DenseNet 출력데이터에 대한 RMSE 경향을 에포크 단위로 그래프로 나타내었다. 이 출력데이터는 OEF 예측에 사용되는 Y를 포함하여 QQ 모델을 구성하고 있는 5개 파라미터(Y, v, R2, S0, χnb)이다.

Fig. 4.

RMSE tendency of model learning

이 그래프를 통해 학습 에포크가 증가함에 따라 RMSE가 감소하며 특정 값에 수렴하는 것을 볼 수 있다. 전반적으로 각 모델의 학습 RMSE는 초기 에포크에서 급격히 감소한 후 안정화되는 경향을 보인다. 검증 데이터는 학습 데이터에 비해 몇몇 에포크에서 튀는 경우가 발생하지만, 전반적으로 유사한 형태를 보이며 에포크가 증가함에따라 수렴하는 경향을 확인할 수 있다. 이는 검증 데이터의 다양성과 복잡성에 의한 것일 수 있다. 이러한 수렴 양상을 통해 모델들이 안정적인 예측 성능을 보이고 있음을 의미한다. 이를 통해 각 모델들이 데이터에 대해 적절하게 학습하여 OEF 예측을 효과적으로 수행할 수 있음을 확인할 수 있다.

4.2 평가 정확도

제안하는 다채널 DenseNet 기반의 모델에서 학습과 검증에 사용하지 않은 11명의 환자 데이터를 사용하여 평가를 진행하였고 평균 RMSE 및 MAE를 계산하여 성능을 비교하였다.

제안하는 모델의 출력은 OEF 계산에 사용되는 정맥 산소포화도 Y 값을 포함한 QQ 모델의 5개의 파라미터로 개별 구성하였다. Y 값만이 OEF 예측에 직접 사용되지만, QQ 모델을 구성하는 모든 파라미터가 다양한 질환 분석에 활용될 수 있기 때문에 5개의 파라미터를 모델의 출력으로 구성하였다[7]. 해당 값들에 대해 성능을 비교하기 위해 에코 타임 0에서 신호 강도 S0, 조직의 가로 이완 R2, 정맥 산소포화도 Y, 정맥 혈액량 v, 비혈류 물질의 자화율 χnb에 대한 Ground Truth와 추정 결과 데이터의 비교를 수행한 평균 RMSE 값을 표 1에 나타내었고, MAE 값을 표 2에 나타내었다.

Table 1.

RMSE of Multi-Channel DenseNet models for evaluation data

Table 2.

MAE of Multi-Channel DenseNet models for evaluation data

이와 같은 결과를 기존 연구들과 비교하기 위하여 동일한 데이터셋을 기반으로 하는 DNN 모델 기반 방법[11]과 LSTM 모델 기반 방법[12]에 대하여 평균 RMSE를 계산하였고 정리한 결과를 표 3에 나타내었다.

Table 3.

RMSE comparison of existing methods and proposed methods

제안하는 다채널 DenseNet 모델은 DNN 모델과 비교했을 때, S0, R2, Y, v, χnb의 모든 지표에서 성능이 개선되었다. 특히, R2와 χnb에서 크게 개선되었고 그 외의 값들에 대해서도 유의미한 성능 개선이 있는 것을 알 수 있다. 또한, LSTM 모델과 비교하였을 때 다채널 DenseNet 모델은 S0, v, χnb에서 더 낮은 오차로 예측되었고 R2, Y에서 상대적으로 조금 높은 오차를 보였다. 비록, OEF 계산에 직접 적용되는 Y의 경우 정확도가 향상되지 않았지만, 그 외의 값들이 전체적으로 개선되었으며 특히, χnb가 크게 개선되었다.

기존 방법들과 비교하였을 때 본 논문에서 제안하는 각 채널을 독립적으로 분리하여 처리하는 다채널 DenseNet 모델이 QQ 모델 파라미터 추정에서 유의미한 결과를 나타내고 있음을 알 수 있고, 그 외의 개선되지 못한 요소는 향후 모델 구조를 개선하거나 각 채널에 대한 DenseNet 모델을 LSTM 모델로 대체하여 오차를 줄일 수 있을 것으로 예상된다.

OEF 예측은 식 (1)과 같이 정맥 산소포화도 Y를 사용하여 계산할 수 있다. 여기서 Ya는 동맥 산소화 값으로 동맥에서의 산소화에 대한 실험을 통해 일반적으로 사용되는 값인 0.98로 가정하였다[9].

$\[ OEF=1-\frac{Y}{Y_a} \]$

(1)

위 식을 사용하여 계산한 환자별 실제 OEF 값과 예측 OEF 값에 대한 비교 결과를 표 4에 나타내었다. 실제 OEF 값과 예측 OEF 값을 보았을 때 전체적으로 원본과 유사한 값으로 예측한 것을 볼 수 있다.

Table 4.

Comparison of Actual OEF and Predicted OEF

기존에 연구되었던 DNN 모델 기반 방법[11], LSTM 모델 기반 방법[12], 본 논문에서 제안하는 다채널 DenseNet 모델을 활용한 방법들의 OEF 예측 결과 평균 RMSE 값을 표 5에 나타내었다. 각 방법들은 비교를 위해 모두 동일한 코넬대학교 의과대학의 데이터셋을 사용하여 진행하였고, 비록 LSTM 모델 기반 방법과 비교하였을 때 좋은 성능을 보이지 못하였으나 충분히 개선이 가능한 수치임을 볼 수 있다. 그러나 S0, v, χnb에서 더 높은 정확도를 나타내어 유의미하다고 할 수 있다.

Table 5.

OEF RMSE of existing methods and proposed methods

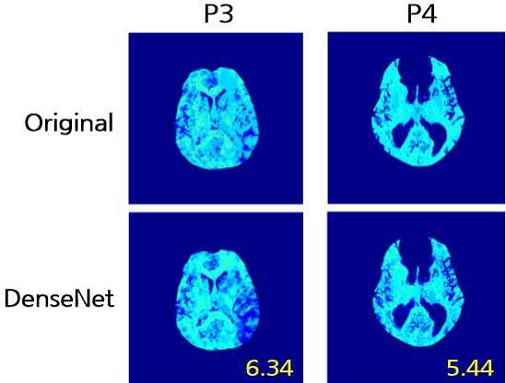
Ground Truth와 제안하는 다채널 DenseNet 모델을 통한 OEF 결과를 비교하여 그림 5에 도시하였고, 제안하는 방법을 통해 예측한 OEF 결과가 Ground Truth 이미지를 비교하였을 때 큰 차이가 없음을 볼 수 있다. 비교적 RMSE 값이 큰 데이터의 경우 일부 영역에서 차이가 있으나, 평균 RMSE인 5.44보다 낮은 데이터의 결과를 비교하였을 때 Ground Truth와 거의 유사한 수준의 결과를 확인할 수 있다. 이를 통해 제안하는 방법의 OEF 예측 결과가 유의미한 정확도를 보임을 알 수 있다.

Fig. 5.

OEF of ground truth and multi-channel DenseNet

Ⅴ. 결론 및 향후 과제

뇌 질환의 높은 사망률과 이에 따른 진단 기법의 다양한 발전으로 환자의 뇌 상태를 정확하게 판단하는 것이 중요해지고 있다. 특히, 뇌 혈액의 산소 소모량을 측정하여 뇌 조직의 활성화 정도를 파악하여 뇌의 상태를 파악할 수 있다.

산소 소모량 계산을 위하여 OEF를 정확하게 예측할 필요가 있으며, 다양한 방법으로 OEF 계산의 정확도를 높이는 방법이 제안되었다.

딥러닝을 활용한 연구도 점진적으로 증가하고 있으며, 본 연구에서는 다채널 DenseNet 모델을 통해 뇌 MRI 영상에서 얻은 데이터를 활용하여 QQ 모델에 기반한 파라미터를 추정하여 유의미한 정확도로 OEF를 예측하는 방법에 대해 제안하였다.

또한, 17명의 환자 데이터를 사용하여 다채널 DenseNet 모델의 학습 및 검증을 수행하였고, OEF 예측에 대한 5.44의 RMSE 정확도로 해당 모델을 통한 OEF 예측이 유의미하다는 것을 보였다.

그러나, LSTM 모델과 비교하였을 때 상대적으로 낮은 정확도를 보인 조직의 가로 이완 R2와 OEF 계산에 사용되는 Y 값에 대해 성능 개선할 필요가 있어서, 향후 연구에서는 새로운 형태의 딥러닝 모델을 적용하거나, 각 채널에 적용한 DenseNet 모델을 LSTM 모델로 교체하여 성능 향상을 모색할 예정이다.

Acknowledgments

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No. RS-2023-00242116)

References

• F. B. Ahmad and R. N. Anderson, "The leading causes of death in the US for 2020", Jama, Vol. 325, No. 18, pp. 1829-1830, Mar. 2021. [https://doi.org/10.1001/jama.2021.5469]
• S. J. X. Murphy and D. J. Werring, "Stroke: causes and clinical features", Medicine, Vol. 48, No. 9, pp. 561-566, Sep. 2020. [https://doi.org/10.1016/j.mpmed.2020.06.002]
• D. Jiang and H. Lu, "Cerebral oxygen extraction fraction MRI: Techniques and applications", Magnetic Resonance in Medicine, Vol. 88, No. 2, pp. 575-600, May 2022. [https://doi.org/10.1002/mrm.29272]
• J. N. Stout, E. Adalsteinsson, B. R. Rosen, and D. S. Bolar, "Functional oxygen extraction fraction (OEF) imaging with turbo gradient spin echo QUIXOTIC (Turbo QUIXOTIC)", Magnetic Resonance in Medicine, Vol. 79, No. 5, pp. 2713-2723, Oct. 2017. [https://doi.org/10.1002/mrm.26947]
• N. Hattori, et al, "Accuracy of a Method Using Short Inhalation of 15O-O2 for Measuring Cerebral Oxygen Extraction Fraction with PET in Healthy Humans", Journal of Nuclear Medicine, Vol. 45, No. 5, pp. 765-770, May 2004.
• X. He, M. Zhu, and D. A. Yablonskiy, "Validation of oxygen extraction fraction measurement by qBOLD technique", Magnetic Resonance in Medicine, Vol. 60, No. 4, pp. 882-888, Sep. 2008. [https://doi.org/10.1002/mrm.21719]
• J. Cho, Y. Kee, P. Spincemaille, T. D. Nguyen, J. Zhang, A. Gupta, S. Zhang, and Y. Wang, "Cerebral metabolic rate of oxygen (CMRO2) mapping by combining quantitative susceptibility mapping (QSM) and quantitative blood oxygenation level-dependent imaging (qBOLD)", Magnetic Resonance in Medicine, Vol. 80, No. 4, pp. 1595-1604, Mar. 2018. [https://doi.org/10.1002/mrm.27135]
• J. Cho, S. Zhang, Y. Kee, P. Spincemaille, T. D. Nguyen, S. Hubertus, A. Gupta, and Y. Wang, "Cluster analysis of time evolution (CAT) for quantitative susceptibility mapping (QSM) and quantitative blood oxygen level-dependent magnitude (qBOLD)-based oxygen extraction fraction (OEF) and cerebral metabolic rate of oxygen (CMRO2) mapping", Magnetic Resonance in Medicine, Vol. 83, No. 3, pp. 844-857, Sep. 2019. [https://doi.org/10.1002/mrm.27967]
• H. Y. Lee, "OEF Calculation Method through Cluster-based Classification and Matching of QQ Model on Brain MRI Images", The Journal of Korean Institute of Information Technology, Vol. 18, No. 10, pp. 15-23, Oct. 2020. [https://doi.org/10.14801/jkiit.2020.18.10.15]
• S. Hubertus, S. Thomas, J. Cho, S. Zhang, Y. Wang, and L. R. Schad, "Using an artificial neural network for fast mapping of the oxygen extraction fraction with combined QSM and quantitative BOLD", Magnetic Resonance in Medicine, Vol. 82, No. 6, pp. 2199-2211, Jul. 2019. [https://doi.org/10.1002/mrm.27882]
• H. S. Kim and H. Y. Lee, "DNN-based Oxygen Extraction Fraction Prediction Method for QQ Model of Brain MRI", The Journal of Korean Institute of Information Technology, Vol. 21, No. 6, pp. 35-41, Jun. 2023. [https://doi.org/10.14801/jkiit.2023.21.6.35]
• W. T. Kim and H. Y. Lee, "Oxygen Extraction Rate Prediction based on LSTM Deep Learning Model using Brain MRI", The Journal of Korean Institute of Information Technology, Vol. 22, No. 6, pp. 143-151, Jun. 2024. [https://doi.org/10.14801/jkiit.2024.22.6.143]
• S.-H. Choi, G.-J. Park, and K.-S. Kim, "Algorithm Implementation of DNN-based Blood Glucose Management Dietary", The Journal of the Institute of Internet, Broadcasting and Communication, Vol. 23, No. 4, pp. 73-78, Aug. 2023. [https://doi.org/10.7236/JIIBC.2023.23.4.73]
• J. Oh and S. Kum, "A Study on Estimating Geomagnetic Azimuth using LSTM", The Journal of the Institute of Internet, Broadcasting and Communication, Vol. 22, No. 6, pp. 137-141, Dec. 2022. [https://doi.org/10.7236/JIIBC.2022.22.6.137]