DSSS 시스템에서 변형 오류 허용 BM 알고리즘 기반 향상된 확산 부호 추정 기법

Ⅰ. 서 론

원래의 신호에 확산부호를 곱하여 신호의 전송대역폭을 확산시키는 직접 시퀀스 대역 확산(DSSS, Direct Sequence Spread Spectrum) 신호는 다중 경로 보상 및 항재밍과 같은 특성을 갖기 때문에 상용 및 군용 통신 시스템에서 널리 사용되고 있다[1]-[3]. 비협력 통신 상황에서 DSSS 시스템이 사용된 경우, 메시지를 복원하기 위해서는 DSSS 신호에 대한 탐지[4] 및 동기화[5], 그리고 DSSS에 사용된 확산부호의 추정이 필요하다.

확산부호의 추정 방법으로 여러 방식의 알고리즘들이 제시되어 왔다[6]-[10]. [6]과 [7]에서는 최적화 기법을 이용하여 효율적으로 최대 우도를 갖는 확산부호를 추정하는 알고리즘을 제시하였다. [8]과 [9]에서는 확산 신호를 이용하여 공분산 행렬의 고유값 분석(EVD, Eigenvalue Decomposition)을 통해 가장 높은 고유값을 갖는 고유벡터를 확산부호로 추정하는 기법을 제시하였다. 최근에는 메시지와 확산부호의 정보를 반복적으로 교대로 반복 추정하며 확산부호를 추정하는 방법이 제시되었다[10].

DSSS 시스템에서는 이상적인 자기상관과 낮은 상호상관을 갖는 선형부호가 확산부호로서 널리 사용된다. 그러나 낮은 신호 대 잡음비(SNR, signal-to-Noise)에서는 효율적으로 확산부호의 선형성을 확인하는 것이 어렵기 때문에 앞에서 언급한 기존 확산부호 추정 알고리즘들은 확산부호의 선형성과 관계없이 확산 신호의 주기성에 기반하여 잡음의 영향을 완화하는 방식으로 확산부호를 추정해 왔다. 따라서, 확산부호를 추정할 때, 확산부호의 선형성을 추가적으로 고려할 수 있다면 추정 정확도를 향상시킬 수 있다.

일반적으로, 수열의 선형성을 고려하기 위해서 입력된 수열을 생성하는 가장 작은 차수의 생성 다항식을 출력하는 BM(Berlekamp-Massey) 알고리즘이 널리 사용된다[11]. 그러나 최초에 제시된 BM 알고리즘은 오류가 없는 수열에만 적용 가능하기 때문에, 이를 보완하기 위해 오류가 있는 수열에도 적용 가능한 오류 허용 BM 알고리즘이 제시되었다[12][13].

본 논문에서는 보다 향상된 확산부호 추정을 위해 오류 허용 BM 알고리즘의 내부 갱신 과정을 변형한 새로운 변형 오류 허용 BM 알고리즘을 제안하고 이를 확산부호 추정에 적용하여 성능을 분석한다. 이를 위해 먼저, 임의의 기존 확산부호 추정 알고리즘을 이용하여 확산부호를 1차 추정한 뒤, 제안하는 변형 오류 허용 BM 알고리즘에 적용한다. 확산부호의 생성 다항식의 차수가 n, 확산부호 길이가 2ⁿ - 1, 최대 허용 오류가 γ로 주어졌을 때, 변형 오류 허용 BM 알고리즘은 내부 재귀 및 입력 수열 갱신을 통하여 입력과 최대 γ의 해밍 거리를 갖는 모든 수열의 생성 다항식 차수가 n인지 확인한 후, 이 중에 n차 생성 다항식을 갖는 선형 수열을 최종 확산부호로 출력한다. 제안하는 기법의 계산복잡도를 살펴보고 컴퓨터 모의실험을 통해 제안한 방법이 높은 추정 성능으로 확산부호를 추정할 수 있음을 검증한다.

본 논문의 구성은 다음과 같다. 2장에서는 시스템 모델과 오류 허용 BM 알고리즘을 소개한다. 3장에서는 확산부호를 추정할 수 있도록 변형된 오류 허용 BM 알고리즘을 제안하며 이를 이용한 확산부호 추정 기법을 제시한다. 4장에서 컴퓨터 모의실험을 통해 제안된 기법의 추정 성능을 검증하며 5장에서 결론을 맺는다.

Ⅱ. 시스템 모델 및 오류 허용 BM 알고리즘

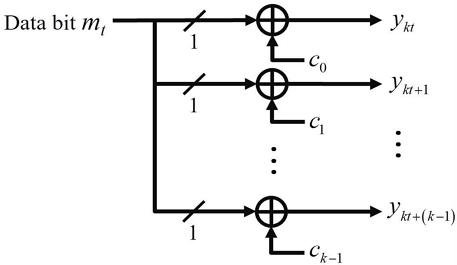
간략화된 DSSS 시스템 모델을 그림 1에 도시하였다.

Fig. 1.

Simplified block diagram of spreader for DSSS system

그림 1과 같이 DSSS 시스템에서 데이터 비트 m_t는 k-비트 확산부호 $$ {\left(c_i\right)}_{i=0}^{k-1}$$에 의해 $$ {\left(y_j\right)}_{j=kt}^{kt+\left(k-1\right)}$$로 확산된다. 이 수열에 잡음이 더해졌을 때, 비협력 상황에서, 송신자는 확산부호에 대한 사전정보 없이 확산부호를 추정해야 한다. 그러나 일반적으로 잡음에 의한 오류로 인해 확산 신호로부터 직접 확산부호를 찾는 것은 매우 도전적이며 어려운 작업이다.

서론에서 언급한바와 같이 DSSS 시스템에서는 선형부호가 확산부호로서 널리 사용된다. 그러나 낮은 SNR에서는 효율적으로 확산부호의 선형성을 확인하는 것이 어렵기 때문에 기존 확산부호 추정 알고리즘들은 확산부호의 주기성에 기반하여 공분산 행렬을 생성함으로써 잡음에 의한 오류의 영향을 완화하는 기법을 주로 사용하며, 공분산 행렬에 최대 우도 기반 방법이나 고유값 분석 등을 적용하여 확산부호를 추정해 왔다. 확산부호를 추정할 때, 확산부호가 선형 부호인 경우, 주기성 외에 확산부호의 선형성을 추가적으로 고려한다면 추정 정확도를 향상시킬 수 있을 것이다. 이를 위해 본 논문에서는 변형 오류 허용 BM 알고리즘을 제시하고 확산부호를 추정하는 방법을 제안한다.

BM 알고리즘은 수열이 주어졌을 때, LFSR(Linear Feedback Shift Register)을 통해 수열을 생성할 수 있는 가장 작은 차수의 생성 다항식을 출력한다. 이 과정에서 BM 알고리즘은 매 입력되는 원소마다 내부 상태를 반복적으로 갱신한다. 이를 설명하기 위해 입력되는 2n-비트 길이 이진 수열을 $$ {\left(s_i\right)}_{i=0}^{2n}$$이라 하자. 그리고 부분수열 $$ {\left(s_i\right)}_{i=0}^j$$을 생성할 수 있는 가장 작은 차수의 생성 다항식을 $$ f\left(x\right)=f_0{x}^a+f_1{x}^{a-1}+\cdots +f_a$$라 하자. 만약 f(x)가 부분수열 $$ {\left(s_i\right)}_{i=0}^{j+1}$$에 대해서도 이를 생성하는 가장 작은 차수의 생성 다항식이라면 추가된 비트 s_{j + 1}에 대해서 a + 1-비트 길이 부분수열 $$ {\left(s_i\right)}_{i=j+1-a}^{j+1}$$은 다음을 만족해야 한다.

여기서 “•”은 내적을 의미한다. 식 (1)에서 d가 0인 경우, f(x)를 이용하여 부분수열을 모두 생성할 수 있으므로 f(x)를 갱신할 필요가 없다. 그러나, d가 1인 경우에는 f(x)가 $$ {\left(s_i\right)}_{i=j+1-a}^{j+1}$$를 생성하지 못하므로 갱신된다. 그리고 f(x)가 갱신되는 경우, 현재 다항식의 차수 a에 대하여 입력된 수열의 길이 j + 1이 2a를 초과한다면 갱신 과정에서 생성 다항식의 차수는 증가하고, 그렇지 않은 경우 동일한 차수의 다른 생성 다항식으로 갱신된다. 이 과정을 반복함으로써 BM 알고리즘은 입력 수열을 생성할 수 있는 가장 작은 차수의 생성 다항식을 출력한다. 그러나 최초에 제시된 BM 알고리즘은 오류가 없는 수열에만 적용 가능하기 때문에, 이를 보완하기 위해 오류가 있는 수열에도 적용 가능한 오류 허용 BM 알고리즘이 제시되었다.

오류 허용 BM 알고리즘은 BM 알고리즘에서 생성 다항식의 차수가 증가하는 경우, 오류가 있는 상황을 가정함으로써 차수가 유지되는 경우를 추가로 고려한다. 생성 다항식의 차수가 증가하는 경우란 구체적으로 a차 생성 다항식과 부분수열 $$ {\left(s_i\right)}_{i=j+1-a}^{j+1}$$에 대해서 (1)의 d가 1이 되면서 동시에 j + 1 > 2a가 되는 경우를 의미한다. 이 때 s_{j + 1}에 오류가 있다고 가정하고 $$ s_{j+1}\leftarrow s_{j+1}\oplus 1$$로 정정하면, $$ d\leftarrow d\oplus 1=0$$이 되면서 생성 다항식이 갱신되지 않아 차수에 변화가 없게 된다. 오류 허용 BM 알고리즘은 그대로의 s_{j + 1}과 정정된 s_{j + 1} 두 경우 모두에 대해 내부 재귀 과정을 수행하고 각각 생성 다항식을 출력한다.

단, 모든 경우에 위와 같이 오류가 있는 경우를 추가하여 고려하는 것은 아니다. 최대 허용 오류 γ를 설정하여 오직 최대 γ개의 오류만 정정하도록 허용한다. 즉, 수열에 이미 γ 개의 오류가 정정된 원소들이 존재한다면 그 이후에는 추가로 오류를 정정하지는 않는다.

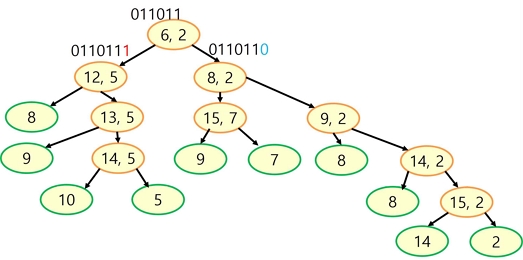
마지막으로, 오류로 정정된 원소가 γ개 이하인 모든 분화된 경우에 대해 얻은 생성 다항식 중에 가장 작은 차수의 생성 다항식을 올바른 생성 다항식으로 출력한다. 그림 2에는 생성 다항식이 $$ x^8+x^6+x^5+x^4+x+1$$ 일 때 생성된 수열 0110111101110101을 γ = 4인 오류 허용 BM 알고리즘에 입력된 경우의 예를 나타내었다.

Fig. 2.

Error-resilient BM algorithm example (γ = 4)

그림 2에서 타원은 식 (1)의 d가 1이 나오고 동시에 j + 1 > 2a가 되어 생성 다항식의 차수가 증가하는 경우들이다. 타원 안의 두 값은 각각 차수가 증가하는 원소 위치와 갱신되기 전의 차수를 의미한다. 예를 들어, 가장 위의 타원에서 (6, 2)란 입력 수열 $$ {\left(s_i\right)}_{i=0}^j$$에서 s₆에 의해 차수가 증가한다는 것을 의미한다. 구체적으로, 6비트 길이 수열 011011을 생성하는 생성 다항식은 2차이고 7비트 길이 수열 011011를 생성하는 경우 더 높은 차수의 생성 다항식으로 갱신되는 것을 나타낸다. 더불어, 왼쪽 화살표와 오른쪽 화살표는 각각 입력 수열의 원소를 갱신하지 않은 경우와 갱신한 경우를 나타낸다. 이에 따라 오른쪽 화살표로 이동하는 경우 수열의 원소가 바뀌고, 생성 다항식의 차수는 유지되는 것을 확인할 수 있다. 그리고 종단에 위치하는 타원들은 수열이 모두 입력되었을 때 출력되는 생성 다항식의 차수들을 의미한다.

III. 변형 오류 허용 BM 알고리즘 및 이에 기반한 확산부호 추정 기법

본 장에서는 변형 오류 허용 BM 알고리즘을 제안하고 이를 이용한 확산부호 추정 방법을 소개한다. 서론에서 언급한대로 이 논문에서는 우선, 임의의 기존 확산부호 추정 알고리즘을 이용하여 2ⁿ - 1-비트 길이의 확산부호 $$ {\left(c_i\right)}_{i=0}^{2^n-2}$$를 1차 추정한다. 이후, 1차 추정된 확산부호를 변형 오류 허용 BM 알고리즘에 적용하여 1차 추정된 확산부호로부터 최대 γ 이하의 해밍 거리를 가지면서 n차 생성 다항식으로부터 생성된 선형 수열을 올바른 확산부호로 추정한다. 이때, 확산부호 추정에 기존 오류 허용 BM 알고리즘 대신에 이를 개선한 새로운 변형 오류 허용 BM 알고리즘이 필요한 이유는 다음과 같다.

첫째, 오류 허용 BM 알고리즘은 언제나 가장 낮은 차수의 생성 다항식을 찾는데 본 논문에서 제안하는 확산부호 추정 기법은 기존 알고리즘으로부터 추정된 초기 확산부호를 이용하기 때문에 이미 확산부호의 생성 다항식의 차수를 알고 있다고 가정할 수 있다. 따라서 가장 낮은 차수의 생성 다항식을 찾는 대신 특정 차수의 생성 다항식을 찾도록 알고리즘을 변형하는 것이 보다 합리적이다. 둘째, 오류 허용 BM 알고리즘은 수열에 있는 오류에 무관하게 차수가 증가하는 경우에만 입력 원소를 갱신한다. 이 경우, 입력 원소에 오류가 존재함에도 생성 다항식의 차수가 증가하지 않으면 원소를 갱신하지 않아 오류가 있는 상황을 고려하지 못하며, 결과적으로 올바른 생성 다항식을 찾지 못하게 된다.

이러한 문제를 해결하기 위하여 확산부호의 올바른 생성 다항식의 차수 n에 대하여 초기 2n 길이의 부분수열에 대해서 모든 가능한 γ 이하의 오류가 있는 경우들을 고려하도록 오류 허용 BM 알고리즘을 변형하여 확산부호 추정에 적용한다. 즉, 기존 확산부호 추정 알고리즘으로부터 1차 추정된 2ⁿ - 1-비트 길이 확산부호 $$ {\left(c_i\right)}_{i=0}^{2^n-2}$$가 주어져 있을 때, 변형 오류 허용 BM 알고리즘에 초기 확산부호를 입력하면 제일 앞 2n-비트 부분수열 $$ {\left(c_i\right)}_{i=0}^{2n-1}$$에 대해서 최대 γ개의 원소를 정정한 모든 가능한 수열들을 고려하여 생성 다항식을 추정한다. 만약 1차 추정된 확산부호에 γ개 이하의 오류가 있다면, 2n-비트 수열 $$ {\left(c_i\right)}_{i=0}^{2n-1}$$에도 γ개 이하의 오류가 있을 것이므로 변형 오류 허용 BM 알고리즘 내에서 오류가 모두 정정된 올바른 2n-비트 길이 부분수열을 고려하여 반드시 올바른 생성 다항식을 얻게 된다.

한편, $$ {\left(c_i\right)}_{i=0}^{2n-1}$$에 오류가 없고 c_i, i > 2n에 오류가 있다면 해당 원소 위치에서 d는 반드시 1이 될 것이다. 이 경우 입력된 부분수열의 길이는 2n을 초과하기 때문에 생성 다항식의 차수는 증가하게 된다. 하지만 이미 올바른 생성 다항식의 차수 n이 주어져 있으므로 갱신된 생성 다항식이 n차를 초과하는 경우 더 이상 생성 다항식을 고려할 필요가 없다.

따라서 변형 오류 허용 BM 알고리즘은 n차를 초과하는 생성 다항식이 등장하는 경우 재귀 과정을 조기 종료한다.

이러한 과정을 바탕으로 제안하는 변형 오류 허용 BM 알고리즘을 나타내면 다음과 같다.

알고리즘 1.

변형 오류 허용 BM 알고리즘 MBMs,n,γ,Px,Tx,Λ,m,d',a,e

알고리즘 1에서 w_H(v)는 수열 v의 해밍 무게이다. 오류 허용 BM 알고리즘에서는 재귀함수를 통해 생성 다항식의 차수를 증가시키는 경우와 오류 수정을 통해 차수를 유지하는 두 가지 경우를 각각 모두 고려하여 재귀 과정을 수행한다. 그러나 알고리즘 1의 단계 4에서 생성 다항식의 차수가 증가하는 경우 차수가 n차보다 커지기 때문에 반드시 오류가 있음을 알 수 있다. 따라서, 이와 같은 경우에 차수가 증가하지 않도록 정정할 뿐 재귀 과정을 수행하지는 않는다.

이에 따라, 알고리즘 1은 단계 1에서 최대 $$ \sum _{i=0}^{\gamma }{}_{2n}{C}_i$$회의 재귀 과정을 수행하며, 나머지 과정은 BM 알고리즘과 같은 계산 복잡도 O(n²)을 갖는다. 일반적으로 m-시퀀스 수열에 대해 n은 확산부호 길이의 k에 대하여 log₂(k + 1)이 되며, 그러면 γ가 2n이라고 해도 최대 $$ 2^{2n}=2^{2{\mathrm{l}\mathrm{o}\mathrm{g}}_2\left(k+1\right)}={\left(k+1\right)}^2$$ 회만 반복되기 때문에 결국 알고리즘 1의 계산 복잡도는 $$ O\left(k^2{\left({\mathrm{l}\mathrm{o}\mathrm{g}}_2\left(k+1\right)\right)}^2\right)$$가 된다.

알고리즘 1을 이용하여 확산부호를 추정하는 과정은 다음과 같이 나타낼 수 있다.

알고리즘 2.

1차 추정된 확산부호에 오류가 γ를 초과하는 경우 올바른 확산부호 대신 틀린 확산부호가 추정되거나 올바른 확산부호를 찾지 못하게 된다. 이러한 경우 알고리즘 2의 단계 2에서는 기존의 1차 추정된 확산부호를 출력하여 추정 정확도가 낮아지는 것을 방지한다.

그리고 최대 허용 오류 γ가 확산부호들의 최소 해밍 거리보다 작아지는 경우, γ 이하의 해밍 거리를 갖는 선형 수열을 찾는 과정에서 알고리즘 1은 틀린 선형 수열을 출력할 수 있다. 따라서 최대 허용 오류는 최소 해밍 거리의 절반 이하로 설정하는 것이 적절하다.

알고리즘 2는 알고리즘 1과 같은 $$ O\left(k^2{\left({\mathrm{l}\mathrm{o}\mathrm{g}}_2\left(k+1\right)\right)}^2\right)$$의 계산 복잡도를 갖는다. 따라서 알고리즘 2를 적용함으로써 발생하는 추가적인 계산 복잡도는 기존의 잘 알려진 EVD 기반 확산부호 추정 알고리즘의 계산 복잡도 O(k³)와 비교할 때 크지 않음을 알 수 있다.

Ⅳ. 모의실험 및 추정 성능

본 장에서는 제안된 기법의 확산부호 추정 정확도 향상을 컴퓨터 모의실험을 통해 보인다. 기존 확산부호 추정 알고리즘으로 잘 알려진 EVD-기반 확산부호 추정 기법을 사용하며 이로부터 1차적으로 추정한 확산부호에 알고리즘 2를 적용한다.

확산되는 메시지 비트의 수는 100, 최대 허용 오류 γ는 5로 설정하여, 총 10,000 회의 모의실험을 수행하였다.

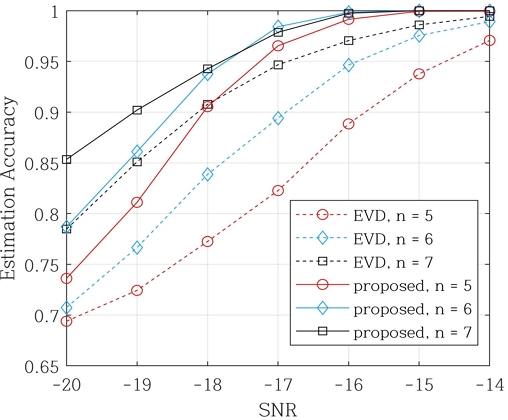
그림 3에는 확산부호의 길이 변화에 따른 확산부호 추정 정확도를 도시하였다. 그림 3에서 모든 확산부호 길이에 대해 제안된 기법이 추정 정확도를 향상시키는 것을 확인할 수 있다.

Fig. 3.

Estimation accuracy according to the degree of the generating polynomial n

1차 추정된 확산부호의 정확도가 높을수록 확산부호의 생성 다항식을 찾기가 쉽기 때문에 높은 SNR에서 더 추정 정확도가 향상됨도 확인 할 수 있다.

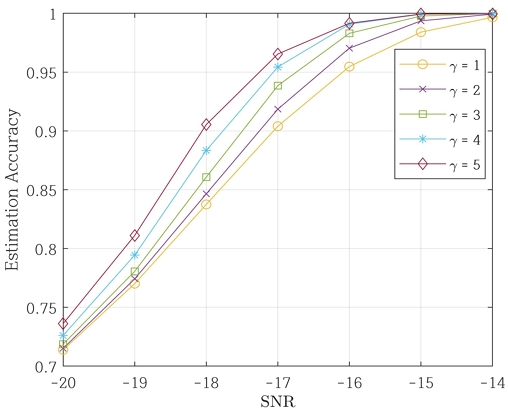
낮은 SNR에서 추정 정확도를 향상시키기 위해서는 허용 오류 수 γ를 높여야 한다. 이를 위해 그림 4에는 n = 5일 때, 최대 허용 오류 γ에 따른 추정 정확도를 도시하였다. 그림 4에서 γ가 증가함에 따라 추정 정확도가 점진적으로 향상되는 것을 확인할 수 있다.

Fig. 4.

Estimation accuracy according to γ

V. 결 론

본 논문에서는 DSSS 수신 신호의 낮은 신호 대 잡음비에서 보다 향상된 확산부호 추정을 위하여 BM 알고리즘의 내부 재귀 과정을 변형한 새로운 변형 오류 허용 BM 알고리즘을 제시하였다. 그리고 이에 기반하여 추정 성능을 향상시킨 확산부호 추정 기법을 제시하고 추정 성능을 분석하였다. 이를 위해 먼저, 임의의 기존 확산부호 추정 알고리즘을 이용하여 확산부호를 1차 추정한 뒤, 제안하는 변형 오류 허용 BM 알고리즘에 적용하였다. 확산부호의 생성 다항식의 차수가 n, 확산부호 길이가 2ⁿ - 1, 최대 허용 오류가 γ로 주어졌을 때, 제안하는 변형 오류 허용 BM 알고리즘은 내부 재귀 및 입력 수열 갱신을 통하여 입력과 최대 γ의 해밍 거리를 갖는 모든 수열의 생성 다항식 차수가 n인지 확인한 후, 이 중에 n차 생성 다항식을 갖는 선형 수열을 최종 확산부호로 출력하였다.

기존 확산부호 추정 알고리즘과 비교했을 때 상대적으로 낮은 추가적인 계산복잡도로 확산부호 추정이 가능함을 보였다. 제시한 알고리즘의 추정 성능을 검증하기 위해 컴퓨터 모의실험을 통해 잘 알려진 기존의 EVD 기반 확산부호 추정 방법과 비교하여 제안된 방법이 높은 추정 성능으로 확산부호를 추정하는 것을 확인하였다.

Acknowledgments

이 논문은 2022년도 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(No. KRIT-CT-22-021, 우주공간 신호정보 특화연구실)

References

• B. Sklar, "Digital Communications: Fundamentals and Applications, Englewood Cliffs", NJ, USA: Prentice-Hall, 2016.
• M. K. Simon, J. K. Omura, R. A. Scholtz, and B. K. Levitt, "Spread Spectrum Communications Handbook", New York, NY, USA: McGraw-Hill, 1994.
• R. L. Peterson, D. E. Borth, and R. E. Ziemer, "An Introduction to Spread-Spectrum Communications", 1st ed. Upper Saddle River, NJ, USA: Prentice-Hall, 1995.
• Y. Kim, G. Kim, H. Kang, J. Kim, and D. Yoon, "Reducing Detection Complexity of Direct Sequence Spread Spectrum Signal by Estimating Cyclic Frequencies", Journal of KIIT, Vol. 20, No. 1, pp. 129-139, Jan. 2022. [https://doi.org/10.14801/jkiit.2022.20.1.129]
• Y. Ju, Y. Kim, J. Kim, H. Kang, J. Song, and D. Yoon, "Blind Synchronization of DSSS Signal using M-Sequence Decimation Propert", Journal of KIIT, Vol. 19, No. 11, pp. 63-70, Nov. 2021. [https://doi.org/10.14801/jkiit.2021.19.11.63]
• S. Mehboodi, A. Jamshidi, and M. Farhang, "Spreading sequence estimation algorithms based on ML detector in DSSS communication systems", IET Signal Process., Vol. 12, No. 6, pp. 802-809, Aug. 2018. [https://doi.org/10.1049/iet-spr.2017.0129]
• Y. Choi, D. Kim, M. Jang, and D. Yoon, "Spreading Sequence Blind Estimation in DSSS System Using Gradient Ascent Method", 2023 33rd International Telecommunication Networks and Applications Conference, Melbourne, Australia, pp. 76-79, Nov. 2023. [https://doi.org/10.1109/ITNAC59571.2023.10368541]
• G. Burel and C. Bouder, "Blind estimation of the pseudo-random sequence of a direct sequence spread spectrum signal", in Proc. MILCOM, Los Angeles, CA, USA, pp. 967-970, Oct. 2000. [https://doi.org/10.1109/MILCOM.2000.904074]
• C. Bouder, S. Azou, and G. Burel, "Performance analysis of a spreading sequence estimator for spread spectrum transmissions", Journal of the Franklin Institute, Vol. 341, No. 7, pp. 595-614, Nov. 2004. [https://doi.org/10.1016/j.jfranklin.2004.07.006]
• H. Choi and H. Moon, "Blind estimation of spreading sequence and data bits in direct-sequence spread spectrum communication systems", IEEE Access, Vol. 8, pp. 148066-14807, Aug. 2020. [https://doi.org/10.1109/ACCESS.2020.3014884]
• J. Massey, "Shift-register synthesis and BCH decoding", IEEE Transactions on Information Theory, Vol. 15, No. 1, pp. 122-127, Jan. 1969. [https://doi.org/10.1109/TIT.1969.1054260]
• M. Stamp and C. R. Martin, "An algorithm for the k-error linear complexity of binary sequences with period 2n", IEEE Transactions on Information Theory, Vol. 39, No. 4, pp. 1398-1401, Jul. 1993. [https://doi.org/10.1109/18.243455]
• Y. Han and G. Yang. "On the k-Error Linear Complexity of p^m-Periodic Binary Sequences and Its Applications to Binary Cyclic Codes", Journal of KICIS, Vol. 31, No. 9C, pp. 846-852, Sep. 2006.