비선형 함수의 대규모 전역 최적화를 위한 Multi-Armed Bandit 기반의 협력 공진화 알고리즘
*국립금오공과대학교 컴퓨터공학과 교수초록
비선형 함수의 전역 최적해를 위한 협력 공진화 알고리즘에서 해 탐색 성능을 강화하기 위해서는 제한된 비용 내에서 목적 함수의 적합도 향상에 가장 큰 영향을 미치는 부분 문제를 발견하고, 해당 부분 문제에 대해 집중적으로 해 탐색을 수행하는 것이 가장 효과적이다. 동시에, 해 탐색의 다양성을 보장하고 조기 수렴을 예방하기 위해서는 여러 부분 문제에 대한 탐색 또한 주기적으로 병행해야 한다. 이에 따라, 본 논문에서는 협력 공진화(CC, Cooperative Coevolution) 알고리즘에서 부분 문제의 선택과 효과적인 최적해 탐색을 위해 MAB(Multi-Armed Bandit) 알고리즘을 활용하는 MAB 기반의 협력 공진화 알고리즘인 MABCC(MAB-based CC)를 제안한다. 실제 1000차원의 비선형 벤치마크 함수를 사용하여 실험을 진행한 결과, 제안하는 MAB 알고리즘 기반의 협력 공진화 알고리즘이 기존에 제안된 협력 공진화 알고리즘보다 더욱 우수한 최적해 탐색 성능을 가짐을 확인하였다.
Abstract
In the cooperative co-evolution(CC) algorithm to search the approximate global optimal solutions of non-linear functions, it is most effective to find the sub-problems with the most significant influence to improve the fitness of objective functions and optimize them intensively to enhance optimization performance. Simultaneously, it is necessary to search various sub-problems to maintain the diversity of solution search and prevent premature convergence problems. Therefore, we propose an MAB-based CC algorithm, i.e., MABCC, to select a significant sub-problem and search for an approximate global optimal solution effectively. We found that our proposed method achieved better solution searchability from the experiments with practical 1000 dimensional large-scale non-linear benchmark functions than the existing CC ones.
Keywords:
global optimization, non-linear optimization, cooperative co-evolution, intelligent optimization, large-scale computation, adaptive computationⅠ. 서 론
최적화이론(Optimization theory)에서 전역 최적화 문제(Global optimization problem)는 다수의 국소 최적점(Local minimum)을 갖는 목적 함수(Objective function)의 적합도(Fitness)를 최소화(또는 최대화)하는 전역 최적해(Global optimal solution)를 탐색하는 문제로 정의된다. 이때 전역 최적화 문제의 복잡성(Complexity)은 목적 함수를 구성하는 결정 변수(Decision variable)의 개수와 이들 간의 상호종속성(Interdependency)에 의해서 결정된다[1]. 특히 결정 변수의 개수가 많고, 이들 간에 복잡한 상호종속성이 존재하는 경우 해당 목적 함수가 생성(Span)하는 해 공간(Solution space)은 많은 수의 국소 최적점과 안장점(Saddle point)을 포함한 복잡한 표면(Surface)을 가지게 되며, 이는 곧 전역 최적해의 정확한 탐색을 어렵게 만드는 요인이 된다. 이러한 높은 복잡도를 갖는 최적화 문제의 경우 전통적인 분석적 또는 수치적 방법으로는 높은 품질의 해를 구하기 어려운 한계가 있다[2].
이에 따라, 전역 최적화 문제를 효과적으로 해결하는 방법의 하나로 진화 알고리즘(Evolutionary algorithm)이 널리 활용되고 있다[3][4][5]. 진화 알고리즘은 자연의 생태계에서 발견되는 적자생존과 진화의 원리를 모방하여 주어진 문제의 최적해를 탐색하는 메타 휴리스틱(Meta-heuristic) 계열의 알고리즘으로, 목적 함수가 생성하는 해 공간을 하나 이상의 개체(Individual)를 이용하여 적응적으로 탐색하면서 근사 전역 최적해를 발견한다[6]. 실제로, 진화 알고리즘은 기존의 전통적인 방법으로는 해결하기 어려웠던 최적화 문제, 특히 비선형 최적화 문제에 대해서 주목할 만한 해 탐색 능력을 갖추고 있음이 여러 연구를 통해서 입증된 바 있다.
그러나 진화 알고리즘을 이용하여 많은 수의 결정 변수로 구성된 비선형 목적 함수의 전역 최적해를 탐색하는 경우 계산적 오버헤드(Computational overhead)가 가중되는 문제점이 있다. 이를 극복하기 위한 방법의 하나로 협력 공진화(CC, Cooperative Coevolution) 알고리즘이 제안되었다[7]. 협력 공진화 알고리즘은 주어진 목적 함수를 더욱 적은 수의 결정 변수들로 구성되는 부분 문제들로 분할한 후, 진화 알고리즘[8]을 이용하여 각 부분 문제에 대한 부분 최적해를 탐색하고, 이들을 조합하여 완전한 근사 전역 최적해를 발견하는 분할 정복법(Divide-and-conquer) 기반의 진화 알고리즘이다.
협력 공진화 알고리즘은 주어진 문제를 작은 크기의 부분 문제로 분할하기 위해 목적 함수를 구성하는 결정 변수 간의 상호종속성을 식별하는 “문제분할 단계”와 진화 알고리즘을 이용하여 부분 문제의 최적해를 탐색하고 이들을 조합하여 전역 최적해를 발견하는 “최적화 단계”로 구성된다[7]. 문제분할 단계에서는 결정 변수 간에 존재하는 상호종속성에 따라 주어진 목적 함수를 하나 이상의 부분 함수로 분리한다. 최적화 단계에서는 각 부분 문제별로 진화 알고리즘을 이용하여 해 탐색을 수행한다. 이때, 대부분의 협력 공진화 알고리즘에서는 목적 함수의 최대 호출 횟수가 제한되어 있으므로 불필요하게 목적 함수를 빈번히 호출하는 경우 실제 최적화 단계 수행에 필요한 목적 함수의 최대 호출 횟수가 감소하게 되므로, 궁극적으로 해 탐색을 충분히 수행할 수 없는 문제점이 발생한다[9].
이처럼 최적화 단계에서 불필요한 목적 함수의 호출을 최소화하기 위해서는 각각의 부분 문제가 실제 전역 최적해 탐색에 얼마나 유의미하게 기여하는가를 평가하고, 이에 기반하여 전역 최적해 품질 향상에 높은 기여도를 갖는 부분 문제에 더 많은 해 탐색 기회를 할당하는 것이 바람직하다. 동시에 발견되는 해의 다양성(Diversity)을 보장하기 위해서는 기여도가 낮은 부분 문제라 할 지라도 해 탐색의 기회가 상실되지 않도록 부분 문제 선택 시 탐색과 활용을 정교하게 제어하는 방법 또한 필요하다. 결과적으로, 협력 공진화 알고리즘은 제한된 계산 자원(목적 함수의 최대 호출 횟수) 내에서 가장 우수한 근사 전역 최적해를 탐색할 수 있도록 각 부분 문제에 대한 해 탐색 기회, 즉, 계산 자원을 할당하는 CRA(Computational Resource Allocation) 문제로 귀결된다.
이에 따라, 본 논문에서는 대규모 차원에서 정의되는 비선형 함수에 대한 최적화(최소화) 문제에서 효과적인 전역 최적해 발견을 위한 MAB(Multi-Armed Bandit) 기반의 협력 공진화 알고리즘인 MABCC(MAB-based CC)를 제안한다. 구체적으로, 협력 공진화 알고리즘에서 부분 문제 선택을 위해 다양한 MAB 알고리즘을 활용하는 방법을 소개하고, 실제 해 탐색 성능에 미치는 영향에 대해 분석한다. 또한 협력 공진화 알고리즘에서 MAB 알고리즘의 활용 가능성과 유의점 그리고 한계점을 고찰한다.
본 논문의 구성은 다음과 같다. 제Ⅱ장에서는 협력 공진화 알고리즘과 MAB 알고리즘의 기본 개념을 설명한다. 제Ⅲ장에서는 MAB 기반의 협력 공진화 알고리즘을 소개하고 구체적인 구현 방법을 설명한다. 제Ⅳ장에서는 실제 협력 공진화 알고리즘에 MAB 알고리즘을 적용했을 때의 성능을 평가하고 그 결과를 분석한다. 마지막으로 제Ⅴ장에서는 본 연구의 결과를 정리하고 의의와 한계점 그리고 향후 연구 방향에 대하여 설명한다.
Ⅱ. 관련 연구
2.1 비선형 전역 최적화 문제의 정의
n차원의 유클리드 공간 Rn에서 정의되는 벡터 에 대해서 Rn에서 R로 사상시키는 비선형 함수 f가 다음과 같이 정의될 때, 함수 f를 목적 함수라 하며 f의 입력 를 구성하는 임의의 변수 xi(1 ≤ i ≤ n)를 결정 변수라 한다.
| (1) |
이때, 함수 f의 최적화 문제는 f를 최소화하는 전역 최적해 를 찾는 문제로 다음과 같이 정의된다.
| (2) |
예를 들면, 아래의 식 (3)은 R2에서 R로 사상하는 비선형 스칼라 함수로, (x1 = 0, x2 = 0)에서 적합도가 최소가 되므로(즉, f([x1,x2]T)= 0) 전역 최적해는 [0,0]T이다.
| (3) |
한편, 함수 f의 정의역 Rn에 속하는 벡터 를 구성하는 임의의 두 결정 변수 xi와 xj (i ≠ j)가 아래의 식 (4)에 정의된 조건을 만족한다면, xi와 xj는 함수 f에서 상호종속성을 갖는다[1][9].
| (4) |
따라서, 식 (4)를 사용하여 모든 변수 쌍 간의 상호종속성을 식별하고 같은 상호종속성을 갖는 변수끼리 클러스터링함으로써 주어진 목적 함수를 하나 이상의 독립적인 부분 문제로 분할할 수 있다.
한편, 식 (4)를 사용하여 n개의 결정 변수 간의 상호종속성을 식별하기 위해서는 O(n2)의 계산 복잡도가 소요된다. 이 경우 함수의 차원이 매우 큰 경우(e.g., 1000 차원 이상), 결정 변수 간의 상호종속성 식별을 위해 목적 함수를 과도하게 호출하게 되어 최적해 탐색에 사용되는 함수의 호출 횟수가 급격하게 감소하게 되고, 결과적으로 해의 품질이 저하되는 문제점이 발생한다. 이에 따라, 목적 함수 내 결정 변수 간의 상호종속성을 식별하는데 소요되는 계산 비용, 즉, 목적 함수의 호출 횟수를 감소시키기 위한 다양한 연구가 진행되었으며, 대표적으로 DG[1], GDG[10], EVIID[11] 등이 있다.
2.2 협력 공진화 알고리즘
1994년에 제안된 협력 공진화 알고리즘은 대규모 차원에서 정의되는 목적 함수의 근사 전역 최적해를 효율적으로 탐색하기 위해 개발된 진화 알고리즘 중 하나이다[8]. 표 1은 근사 전역 최적해의 탐색을 위한 협력 공진화 알고리즘의 의사코드를 보여준다. 표 1에 기술된 바와 같이 협력 공진화 알고리즘은 분할 정복법의 원리에 기반하여 주어진 문제를 더욱 작은 크기의 부분 문제로 분할하는 “문제분할 단계(Problem decomposition step)”와 각 부분 문제에 대한 부분 최적해의 탐색을 수행하여 전체 최적해를 발견하는 “최적화 단계(Optimization step)”로 구성된다.
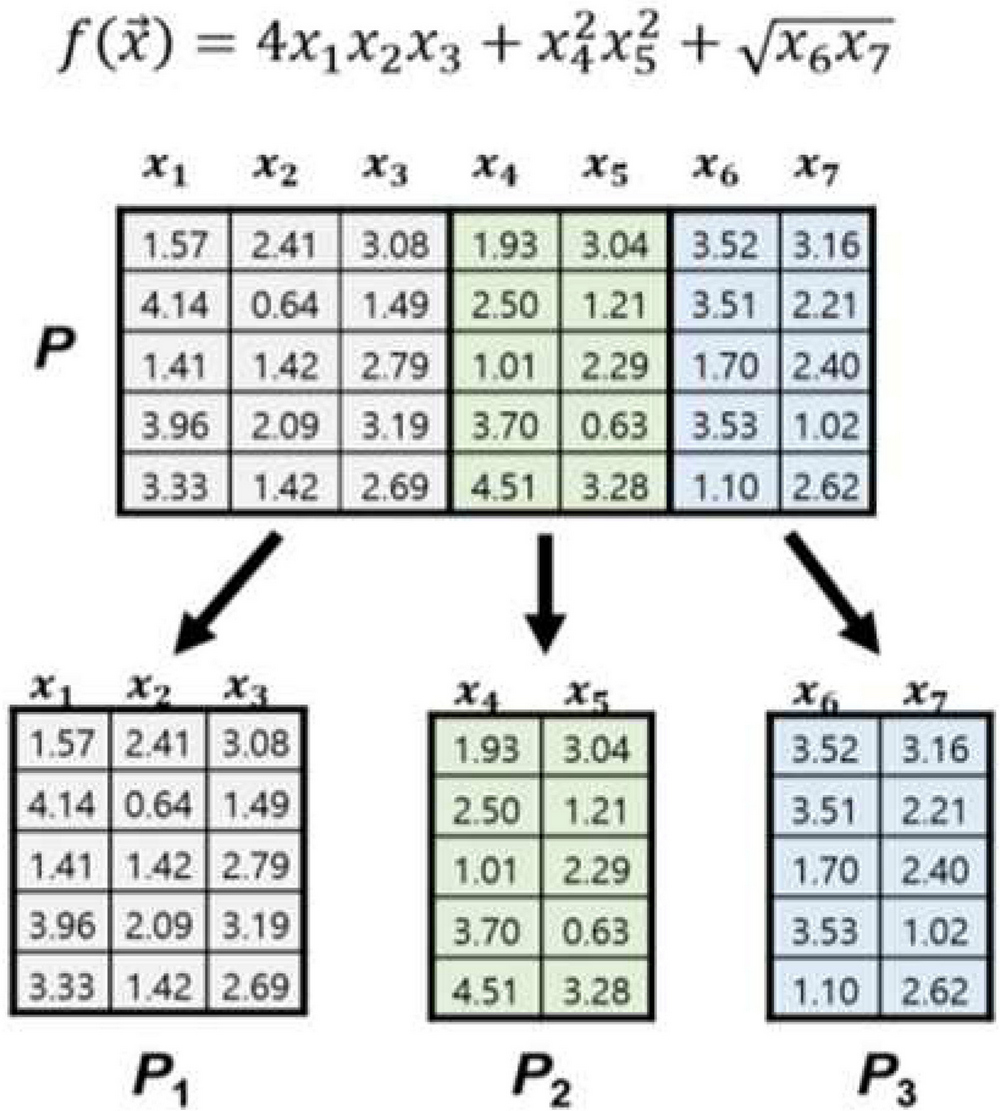
문제분할 단계에서는 2.1절에서 설명한 문제분할 방법에 따라 주어진 목적 함수를 하나 이상의 부분 문제로 분할한 후 각 부분 문제에 대한 부분 최적해를 탐색하고 이들을 조합하여 근사 전역 최적해를 발견한다. 이때, 목적 함수의 경우 사전에 구체적인 형태가 알려지지 않은 Black-Box Function으로 주어지는 것이 일반적이다. 이 경우, 각 부분 문제의 최적해를 탐색하기 위해서 먼저 해당 부분 문제를 구성하지 않는 변수(차원)의 값은 임의의 상수로 고정한다. 그다음, 해당 부분 문제를 구성하는 변수들에 대해서만 해 탐색을 진행한다. 예를 들면, 식 (5)의 함수는 식 (4)에 의해서 V1 = {x1,x2,x3}으로 구성되는 부분 문제 B1과 V2 = {x4,x5}로 구성되는 부분 문제 B2, 그리고 V3 = {x6,x7}로 구성되는 부분 문제 B3로 분할된다.
| (5) |
이때, 현재 시점 t까지 발견된 전역 최적해를 식 (6)이라 가정하면, 첫 번째 부분 문제 B1에 대한 해 탐색을 수행하기 위해서는 다른 부분 문제 B2와 B3를 구성하는 결정 변수 x4, ..., x7의 값은 상수로 고정하고, B1을 구성하는 결정 변수 x1, x2, x3의 차원에 대해서만 해 탐색을 진행한다.
| (6) |
최적화 단계에서는 각 부분 문제의 최적해를 발견하기 위해서 하나 이상의 개체를 포함하는 집단(Population)을 운용한다. 집단 P는 n차원의 개체 m개로 구성되는 m × n의 실수 행렬이다. P의 i번째 부분 집단 Pi는 P의 부분 행렬로, Vi 내 결정 변수에 대응되는 차원의 열벡터(Column vector)들로 구성되며, 다음과 같이 표현된다.
| (7) |
즉, 집단 P = Rm×n의 부분 집단 Pi는 식 (7)을 만족하는 P의 부분 행렬이며, 이때 P[:,xj]는 P에서 결정 변수 xj에 대응되는 차원을 추출한 열벡터이고 ⊕는 행의 크기가 동일한 두 행렬을 가로로 결합하는 연산(Concatenation)을 의미한다.
그림 1은 식 (5)의 함수 의 전역 최적해 탐색을 위해 운용되는 집단 P가 부분 집단 P1, P2, P3로 분할되는 방법을 보여준다. 예를 들어, P1은 부분 문제 B1의 결정 변수 집합 V1에 따라 P에서 1, 2, 3번째 열벡터를 추출함으로써 구성된다. P2와 P3 역시 P1과 같은 원리로 생성된다.
각 부분 문제별로 부분 집단을 구성한 후에는 진화 알고리즘을 이용하여 부분 집단 Pi의 부분 최적해를 탐색한다. 이 과정에서 각 개체별로 적합도를 측정하여 가장 좋은 적합도를 갖는 개체를 Pi의 부분 최적해로 결정한다. 이러한 최적해 탐색 과정은 표 1의 12번째 줄에 기술된 바와 같이 부분 집단 Pi에서 개체 적합도 평가에 사용된 목적 함수의 호출 횟수 가 최대 함수 호출 횟수 Ψ를 초과할 때까지 모든 부분 문제에 대하여 반복적으로 수행한다. 마지막으로, 진화 연산을 통해서 최적화된 부분 집단들을 하나로 합친 전체 집단 P에서 가장 좋은 적합도를 갖는 개체를 전역 최적해로 반환하면서 알고리즘이 종료된다.
2.3 Multi-armed bandit 알고리즘
강화학습(Reinforcement learning)에서 MAB(Multi-Armed Bandit) 문제란 현재 시점에서 단 하나의 Arm만 선택하여 수행하고 이에 대한 보상(Reward)을 획득하는 일련의 의사결정 과정(Decision process)으로, 전체 수행 과정에서 획득한 보상의 총합이 최대가 될 수 있도록 각 시점에서 최적의 Arm을 선택하는 문제이다[12]. 이때, 각 시점에서는 K개의 Arm 중에서 단 하나만을 선택할 수 있으며, 각 Arm이 제공하는 보상은 다른 Arm과는 독립적인 고유의 분포(Independently identically distribution)에 따라 결정된다.
이러한 조건에서 최대의 보상을 달성하기 위해서는 Arm을 선택하는 과정에서 탐색(Exploration)과 활용(Exploitation)의 균형을 적절하게 유지하는 것이 중요하다. “탐색”이란 다양한 Arm의 수행을 통해 각 Arm에 대한 정보를 취합하는 과정을 의미한다. 최적화 관점에서 탐색은 집단 내에서 해 탐색의 다양성을 강화하는 데 중요한 기능을 수행한다. 한편, 해 탐색의 수렴 속도를 강화하기 위해서 탐색에서 수집된 정보에 기반하여 높은 보상을 제공할 것으로 예상되는 Arm을 집중적으로 선택하여 수행하는 것을 “활용”이라 한다. 만약 지나치게 탐색에만 집중한다면 높은 보상을 달성하는 데 도움이 되지 않는 불필요한 Arm을 반복적으로 선택하게 되므로 해의 수렴 속도가 느려지게 된다. 반대로 과도하게 활용에만 치중한다면 장기적으로 더 좋은 보상을 제공할 수 있는 다른 Arm의 수행 기회를 상실하여 궁극적으로 해가 조기에 수렴하는 Premature Convergence 현상이 발생할 수 있다. 따라서 탐색과 활용의 균형을 적절하게 유지하여 Arm을 선택함으로써, 전체 보상을 극대화하는 것이 MAB 알고리즘의 핵심 목표라 할 수 있다. 즉, T번의 수행 과정에서 획득한 보상의 총합과 실제 최적 보상 값 간의 차이를 최소화할 수 있어야 하며, 이는 아래와 같이 Regret Bound를 이용하여 정의된다[12].
| (8) |
상기 수식에서 θ*는 실제 최적의 보상 값을, E[rt]는 시점 t에서 획득할 수 있는 보상의 기대값을 의미한다. 또한, I(A(t) = i)는 시점 t에서 i번째 Arm을 선택하면 1을 아니면 0을 반환하는 Indicator Function이다.
그러나 대부분의 MAB 문제에서는 실제 최적의 보상 값인 θ*가 주어지지 않기 때문에 식 (8)과 같은 Regret Bound를 직접적으로 활용할 수 없다. 이러한 한계점을 극복하기 위해서, 전체 보상의 기대값을 가능한 최대화할 수 있는 근사 MAB 알고리즘(Approximate MAB algorithm)이 개발되었다. 대표적인 근사 MAB 알고리즘으로, ϵ-Greedy, ϵ-First, ϵ-Decrease, UCB(Upper Confidence Bound) 1, UCB1-Tuned, UCB2 등이 있다[12][13]. 이러한 근사 MAB 알고리즘은 네트워크에서의 라우팅 최적화 문제[14]와 UAV 경로 할당 및 최적화 문제[15] 등 다양한 최적화 문제의 해결을 위해 널리 활용되고 있다.
Ⅲ. MAB 기반 협력 공진화 알고리즘
본 장에서는 협력 공진화 알고리즘에서 부분 문제 선택을 위한 방법으로 MAB 알고리즘을 활용하는 방법과 이에 기반한 새로운 협력 공진화 알고리즘인 MABCC(MAB-based CC) 알고리즘을 제안한다. 또한 MABCC 알고리즘의 구현 방법을 구체적으로 설명한다.
3.1 MAB 문제와 협력 공진화 알고리즘의 비교
앞서 표 1에서 언급한 바와 같이 전통적인 협력 공진화 알고리즘은 각 부분 문제에 대하여 순차적으로 진화 알고리즘을 적용하여 최적해를 탐색하는 Round-Robin 기반의 부분 문제 최적화 전략을 사용한다. 그러나 목적 함수를 구성하는 결정 변수들이 적합도 향상, 즉 전역 최적해 탐색에 영향을 미치는 정도는 상이하다. 이때, 전역 최적해 탐색에 영향력이 적은 부분 문제에 대해서 해 탐색을 빈번하게 수행하는 경우 계산 자원, 즉 해 탐색에 필요한 목적 함수의 최대 호출 횟수(표 1에서 Ψ)를 낭비하게 되어 결과적으로 다른 부분 문제에 대한 해 탐색의 기회를 감소시킨다. 이는 곧 전역 최적해의 품질이 저하되는 요인으로 작용한다.
이러한 문제점을 해결하기 위해서는 각 부분 문제가 실제 목적 함수의 적합도 향상에 얼마만큼 기여하는가를 평가하고, 이에 기반하여 기여도가 높은 부분 문제를 중심으로 해 탐색을 수행해야 한다. 아울러, 높은 기여도를 갖지 않는 부분 문제라 할 지라도 해 탐색 과정에 참여할 수 있도록 보장하여, 해 탐색의 다양성을 확보할 수 있어야 한다. 즉, 부분 문제 선택에 있어서 탐색과 활용의 균형을 적절하게 유지하는 것이 중요하다.
그러나 부분 문제를 선택하는 시점에서 각 부분 문제가 적합도 향상에 얼마만큼 기여할 수 있는가를 사전에 파악하는 것은 불가능하다. 대신, 각 시점에서 선택된 부분 문제에 대해서만 해 탐색을 수행한 후 전역 최적해의 적합도 평가를 통해 해당 부분 문제가 적합도 향상에 얼마만큼 기여했는가를 평가할 수 있다. 이는 앞서 Ⅱ장에서 설명한 MAB 문제의 특성과 정확하게 일치한다. 실제 MAB 알고리즘과 협력 공진화 알고리즘의 특징을 비교하면 표 2와 같다.
협력 공진화 알고리즘을 MAB 문제로 모델링하기 위해서는 각 부분 문제를 선택하여 해 탐색을 진행한 후, 전역 최적해의 적합도 평가를 통해 기여도를 측정하는 방법과 이에 기반하여 각 시점에서 최적의 부분 문제를 선택하는 방법이 구체적으로 정의되어야 한다. 이는 다음에 이어지는 3.2 - 3.3장에서 자세히 다루어진다.
3.2 부분 문제의 보상과 기여도
MAB 알고리즘에서 각각의 Arm은 다른 Arm과는 독립적인 고유의 분포(Independently Identically Distribution)에 따라 보상을 제공한다[15][16]. 이와 유사하게 협력 공진화 알고리즘에서 각각의 부분 문제는 식 (4)와 (5)에서 설명한 바와 같이 다른 부분 문제들과 상호 독립적(Mutually independent)이므로, 각 부분 문제는 해당 목적 함수의 전역 최적해를 탐색하는 데 독립적인 기여를 가진다. 따라서, 협력 공진화 알고리즘에서 특정 부분 문제에 대하여 해 탐색을 수행한 후 발견된 전역 최적해의 적합도가 기존의 적합도와 비교했을 때 얼마만큼 향상되었는가를 측정함으로써 해당 부분 문제의 기여도를 계산할 수 있다. 이때, 각 시점에서 발견되는 전역 최적해의 적합도 향상 비율은 해 탐색이 진행될수록 해가 수렴함에 따라 점차 감소하게 된다. 따라서, 각 시점에서 측정된 부분 문제의 기여도를 효과적으로 비교하기 위해서는 적합도 향상의 정도를 특정 범위로 스케일링(Scaling)하는 작업이 수반되어야 한다. 결과적으로, 현재 시점에서 i번째 부분 문제 Pi에 대한 기여도 점수는 다음과 같이 계산할 수 있다.
| (9) |
상기 식 (9)에서 fprevious는 이전 시점에서 측정된 전역 최적해의 적합도를 의미하며 fcurrent는 현재 시점에서 부분 문제 Pi에 대한 해 탐색을 수행한 후 발견된 새로운 전역 최적해의 적합도를 나타낸다. 또한 τ는 분모가 0이 되는 것을 방지하는 Smoothing Factor이다. 이때, fcurrent와 t에서의 전역 최적해 는 다음과 같이 계산된다.
| (10) |
즉, 진화 연산을 통해서 부분 문제 Pi에 대한 해 탐색이 완료되면, 전체 집단 P에 새롭게 업데이트된 Pi가 반영된다. 이후, P의 모든 개체(Individual)에 대하여 적합도를 계산하고, 가장 좋은 적합도 fcurrent를 갖는 개체 P[j, :]가 가 된다.
식 (9)에서 계산된 i번째 부분 문제의 기여도 점수 Si는 현재 시점에서 i번째 부분 문제를 최적화함에 따라 f의 전역 최적해를 탐색하는 데 얼마만큼 기여했는가를 정량적으로 보여주는 지표라 할 수 있다. 따라서 Si는 다음 탐색 시점에서 최적의 부분 문제를 선택하기 위한 핵심 정보로 활용될 수 있다.
3.3 최적의 부분 문제 선택 전략
식 (9)를 이용하여 측정된 각 부분 문제의 기여도에 기반하여, 현재 시점 t에서 전역 최적해 향상에 가장 크게 기여할 것으로 예상되는 부분 문제를 선택할 수 있다. 이때, 기여도가 가장 높은 부분 문제만을 집중적으로 선택하여 해 탐색을 수행한다면 다른 부분 문제에서의 해 탐색을 통해서 달성할 수 있는 해의 다양성(Diversity)이 감소하게 된다. 이는 곧 국소 최적점으로 해가 조기에 수렴하여 결과적으로 최적화 성능이 저하되는 현상을 초래한다. 반면에, 해 탐색의 다양성을 강화하기 위해 기여도를 고려하지 않고 부분 문제를 선택하는 과정을 반복한다면, 해 탐색의 수렴 속도가 저하되어 결과적으로 제한된 최대 함수 호출 횟수 이내에 전역 최적해를 발견하지 못하는 문제가 발생한다. 이처럼 부분 문제 선택 시 탐색과 활용의 적절한 균형을 유지하기 위해 본 논문에서는 MAB 알고리즘을 활용한 부분 문제 선택 방법을 제안한다.
표 3은 본 논문에서 제안하는 MAB 알고리즘 기반의 협력 공진화 알고리즘인 MABCC 알고리즘의 의사코드를 나타낸 것이다. 표 1의 전통적인 협력 공진화 알고리즘과는 달리, 본 논문에서 제안하는 MABCC 알고리즘은 각 시점 t에서 해 탐색을 수행할 부분 문제를 선택하기 위해서 MAB 알고리즘을 사용한다. 이를 위해, MABCC 알고리즘을 최초로 수행할 시 모든 부분 문제에 대하여 한 번씩 해 탐색을 수행하고, 각 부분 문제별로 적합도 향상에 대한 기여도를 평가한다.
이때, 각 부분 문제의 기여도는 식 (9)를 이용하여 계산하고 별도의 변수에 저장하여 부분 문제 선택 시 MAB 알고리즘에서 활용할 수 있도록 하였다.
모든 부분 문제에 대한 해 탐색을 한 번씩 수행한 후, 각 시점 t에서 해 탐색을 수행할 부분 문제를 MAB 알고리즘을 이용하여 결정한다. 표 4는 부분 문제 선택을 위한 MAB 알고리즘의 의사코드를 보여준다. 표 4에 기술된 바와 같이, MAB 함수는 ϵ-Greedy 계열 MAB 알고리즘 2종과 UCB 계열 알고리즘 3종, 총 5종의 MAB 알고리즘 중 하나를 선택하여 사용할 수 있도록 설계되었다.
표 4의 MAB 알고리즘은 공통적으로 각 부분 문제에 대하여 계산된 모든 기여도 값을 활용하여 부분 문제를 선택한다. 이를 위해, MABCC 알고리즘은 각 부분 문제에 대하여 최적해 탐색이 수행될 때마다 기여도를 계산하여 변수 Sj,nj에 저장한다. 즉, j번째 부분 문제에 대하여 해 탐색을 수행할 때, 해당 부분 문제가 선택된 횟수를 변수 nj에 기록하고, 이때의 기여도를 Sj,nj에 저장한다. 이를 통해, 표 4의 MAB 알고리즘은 최적의 부분 문제를 선택하기 위해서 각 부분 문제의 기여도 변수 S1,...,SK의 평균과 분산을 계산하여 부분 문제 선택에 활용할 수 있다. 이후, 각 MAB 알고리즘의 Arm 선택 전략에 따라 최적의 부분 문제를 선택하면, 표 3의 MABCC 알고리즘에서는 해당 부분 문제에 대한 해 탐색을 진행한다. 이러한 과정은 목적 함수의 최대 호출 횟수 Ψ를 초과할 때까지 반복적으로 진행된다. 마지막으로, 최종 발견된 전역 최적해 x*를 반환한 후 알고리즘이 종료된다.
이처럼 부분 문제 선택을 위해 MAB 알고리즘을 사용하는 방법은 Round-Robin 방법이나 랜덤하게 부분 문제를 선택하는 전통적인 협력 공진화 알고리즘과 가장 대비되는 특성이라 할 수 있다. 구체적으로, 전통적인 협력 공진화 알고리즘의 경우 전역 최적해 탐색에 유의미한 영향을 미치지 않는 부분 문제에 대해서도 일정 횟수 이상의 해 탐색을 수행하게 된다. 이는 곧 목적 함수를 불필요하게 호출하여 결과적으로 전역 최적해 탐색에 기여도가 높은 부분 문제에서 해 탐색을 수행하는 데 필요한 목적 함수의 호출 가능한 횟수를 제한하게 된다.
이는 곧 최종적으로 발견되는 전역 최적해의 품질이 낮아지게 되는 요인으로 작용한다. 반면에 본 논문에서 제안하는 MAB 기반의 협력 공진화 알고리즘의 경우 전역 최적해 탐색에 낮은 기여도를 갖는 부분 문제보다는 상대적으로 높은 기여도를 갖는 부분 문제에 대해 더 많은 해 탐색 기회를 부여함으로써 더욱 우수한 적합도를 갖는 전역 최적해를 발견할 가능성을 높일 수 있다.
동시에 MAB 알고리즘을 통해 부분 문제 선택 시 탐색과 활용의 균형을 적절하게 조화시킴으로써 해 탐색의 다양성을 보장하는 효과 또한 기대할 수 있다.
Ⅳ. 실 험
4.1 실험 구성 및 방법
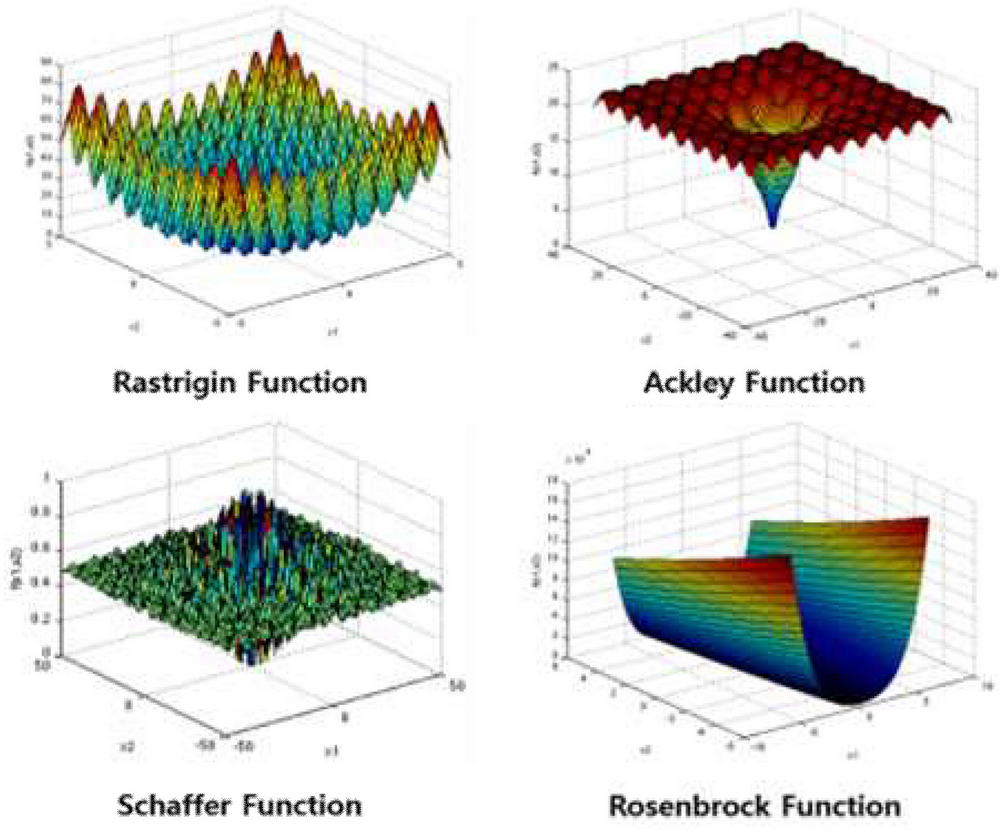
실제 대규모 비선형 함수에 대해서 MABCC 알고리즘의 최적화 성능을 평가하기 위한 실험을 진행하였다. 첫째, 성능 평가를 위한 Benchmark Function으로 IEEE Congress on Evolutionary Computation (CEC) 2010 Benchmark Suite[16]에 포함된 18개의 Non-linear Optimization Function 들을 사용하였다. CEC 2010 Benchmark Function은 그림 2와 같이 최적화 알고리즘의 성능 평가를 위해서 특별히 고안된 Rastrigin Function, Ackley Function, Schaffer Function, Rosenbrock Function과 같은 다양한 함수들[17]이 1000차원의 해 공간에서 분리 가능 부분 문제들과 분리 불가능한 부분 문제들의 합으로 구성되어 있으며, 대규모 전역 최적화 알고리즘의 해 탐색 성능을 평가하기 위한 Benchmark Problem으로 널리 활용되고 있다.
둘째, 각 부분 문제에 대응되는 집단에 대한 해 탐색을 수행하기 위한 진화 알고리즘으로 차분 진화(DE, Differerential Evolution) 알고리즘[18]을 적용하고, 차분 진화 알고리즘의 해 탐색 전략으로 “DE/Current-to-Best/1”을 사용하였다. DE/Current-to-Best/1 전략은 해 탐색 과정에서 각 개체의 현재 위치(Current position)와 현재 시점에서 최적의 적합도를 갖는 개체(Best individual)의 위치를 기준으로 탐색 방향을 결정하고, 이에 따라 해 탐색을 진행하는 방법이다. 또한, 주어진 함수 내 결정 변수 간의 상호종속성을 식별하여 여러 개의 부분 문제로 분할하는 “문제분할 알고리즘”은 2020년에 발표된 EVIID[11] 알고리즘을 사용하였다.
셋째, 18개의 Benchmark Function 각각에 대하여 총 25회 반복하여 실험을 진행하였다. 이때, 각 Benchmark Function에 대한 25개 최적해의 평균 적합도를 해당 Benchmark Function에 대한 실험 결과값으로 활용하였다.
마지막으로, 각 Benchmark Function에 대하여 각각의 협력 공진화 알고리즘이 발견한 전역 최적해들의 평균 적합도를 상호 비교하기 위하여 윌콕슨 순위합 검정(Wilcoxon rank-sum test)을 실시하였다. 이때, 검정을 위한 유의 수준(Significance level) p는 0.05로 설정하여 실험을 진행하였다.
4.2 MAB 알고리즘의 종류에 따른 성능 비교
표 4에서 언급한 바와 같이, 본 연구에서는 협력 공진화 알고리즘에서 부분 문제 선택을 위한 방법으로 ϵ-First, ϵ-Decrease, UCB1, UCB1-Tuned, UCB2를 채택하였다. 따라서, 이들 각각을 기반으로 구현한 협력 공진화 알고리즘 사용하였을 때의 최적해 탐색 성능을 평가하였다.
표 5는 상기 MAB 알고리즘이 적용된 MABCC 알고리즘 각각이 나머지 다른 MAB 알고리즘이 적용된 MABCC 알고리즘과 비교했을 때, 몇 개의 Benchmark Function에서 더 좋은/동등한/더 낮은 적합도를 갖는 전역 최적해를 발견하였는가를 분석한 결과이다. 표 5에서 “Target MABCC Algorithm”은 성능 평가의 목표가 되는 MABCC 알고리즘을 나타내며, 해당 Target Algorithm에 대응되는 나머지 “Compared MABCC Algorithm”들은 “Target Algorithm”과 비교 대상이 되는 다른 MABCC 알고리즘을 의미한다. 각 Target MABCC 알고리즘의 “Win”과 “Tie”, “Lose”는 해당 Target MABCC 알고리즘에 의해서 발견된 전역 최적해의 평균 적합도가 Compared MABCC 알고리즘에 의해서 탐색 된 전역 최적해의 평균 적합도와 비교했을 때, “더 좋은” / “동등한” / “더 낮은” 것으로 평가된 Benchmark Function의 개수를 의미한다.
표 5에 제시된 바와 같이, UCB1-Tuned 알고리즘을 적용한 MABCC-UCB1-Tuned 알고리즘이 대부분의 Benchmark Function에서 다른 MAB 알고리즘을 적용한 MABCC 알고리즘보다 더 좋거나 동등한 적합도를 갖는 최적해를 탐색할 수 있음을 확인하였다.
우선, ϵ-Greedy 계열 알고리즘이 적용된 협력 공진화 알고리즘인 MABCC-ϵ-First 및 MABCC-ϵ-Decrease와 MABCC-UCB1-Tuned의 결과를 비교하면, 총 12개의 Benchmark Function에서 MABCC-UCB1-Tuned가 더 좋은 적합도를 갖는 최적해를 발견한 것으로 확인되었다.
한편, UCB2가 적용된 협력 공진화 알고리즘인 MABCC-UCB2와 MABCC-UCB1-Tuned의 성능을 비교한 결과 모든 Benchmark Function에서 MABCC-UCB1-Tuned가 더 좋거나 동등한 적합도를 갖는 최적해를 발견하였음을 확인하였다. 요약하면, MABCC-UCB1-Tuned와 다른 4개의 MABCC 알고리즘과의 최적화 성능을 비교한 결과 총 72개의 Benchmark Function Test 중 32(28)개에서 MABCC-UCB1-Tuned가 더 좋은(동등한) 적합도를 갖는 최적해를 발견한 것으로 확인되었다.
한편, ϵ-First와 ϵ-Decrease, UCB1, UCB2가 적용된 MABCC 알고리즘 각각에 대해서도 다른 MAB 방법이 사용된 알고리즘과의 비교를 통해 최적화 성능을 확인하였다. 그 결과, MABCC-UCB2의 경우 총 72개의 Benchmark Function Test 중 26(26)개의 Test에서 다른 협력 공진화 알고리즘보다 더 좋은(동등한) 적합도를 갖는 최적해를 발견하였음을 확인하였다. 이에 따라, 본 연구에서는 총 다섯 가지 MABCC 알고리즘 중 가장 좋은 최적해 탐색 결과를 보인 “MABCC-UCB1-Tuned”를 중심으로 기존의 다른 협력 공진화 알고리즘과의 최적해 탐색 성능을 비교하는 실험을 진행하였다.
4.3 기존 협력 공진화 알고리즘과의 성능 비교
표 6은 각 Benchmark Function에 대해서 MABCC-UCB1-Tuned와 다른 기존의 협력 공진화 알고리즘에 의해서 수행된 최적화 결과를 보여준다. 각 Benchmark Function에서 “Mean”은 협력 공진화 알고리즘이 25회의 독립적인 반복 실험을 통해서 발견한 25개의 최적해 적합도 값들의 평균을 의미한다. “p-value”는 MABCC-UCB1-Tuned 알고리즘에 의해서 수행된 결과(Mean)와 해당 협력 공진화 알고리즘에 의해서 수행된 결과 간의 동등성을 확인하기 위한 윌콕슨 순위합 검정 결과로, p-value가 0.05 보다 크면 서로 동등한 결과(Tie)로, 그렇지 않으면 상이한 결과(Win or Lose)로 판단한다.
실험 결과, 기존의 다른 협력 공진화 알고리즘과 비교했을 때, 대부분의 Benchmark Function에서 MABCC-UCB1-Tuned가 더 좋은 최적해 탐색 능력을 갖춘 것으로 확인되었다. 첫 번째 비교 대상 협력 공진화 알고리즘인 BasicCC는 표 1을 그대로 구현한 것으로, 모든 부분 문제를 순차적으로 선택하는 전통적인 협력 공진화 알고리즘이다. BasicCC 알고리즘과의 최적화 성능을 비교한 결과, 본 논문에서 제안하는 MABCC-UCB1-Tuned 알고리즘이 모든 Benchmark Function에서 BasicCC보다 더 좋거나 동등한 수준의 최적해를 발견하였음을 확인하였다. 구체적으로, MABCC-UCB1-Tuned 알고리즘이 총 10개의 Benchmark Function에서 BasicCC보다 더 좋은 최적해를, 8개의 Function에서 동등한 적합도를 갖는 최적해를 발견한 것으로 분석되었다.
두 번째 비교 대상인 BBCC[19]는 MAB 알고리즘 중 ϵ-Greedy 방법을 이용하여 부분 문제를 선택하는 방법을 최초로 시도한 협력 공진화 알고리즘으로, MABCC-UCB1-Tuned 알고리즘보다 더 낮은 최적해 탐색 성능을 달성하였다. 이는, 앞서 설명한 다른 MAB 알고리즘을 적용한 협력 공진화 알고리즘의 성능 평가 결과에서 확인한 바와 같이, 협력 공진화 알고리즘에서 부분 문제를 선택하는 MAB 알고리즘으로 UCB1-Tuned 알고리즘을 사용함으로써 가장 좋은 최적해 탐색 성능을 달성할 수 있음을 보여주는 결과라 할 수 있다.
마지막으로, CBCC1과 CBCC2는 각 부분 문제의 최적해 탐색 수행 전과 후에 발견된 전역 최적해의 적합도 향상 정도에 따라 다음 시점에서 해 탐색을 수행할 부분 문제를 결정하는 순수 기여도 기반의 협력 공진화 알고리즘(Contribution-based CC Algorithm)이다[20]. CBCC1 및 CBCC2와의 실험 결과 비교에서, MABCC-UCB1-Tuned 알고리즘이 18개와 13개의 Benchmark Function에서 CBCC1 및 CBCC2 보다 더 좋거나 동등한 적합도를 갖는 최적해를 발견한 것으로 확인되었다.
상기의 실험 결과를 통해서, 협력 공진화 알고리즘에서 부분 문제의 선택을 위해 MAB 알고리즘, 특히 UCB1-Tuned와 UCB2와 같은 UCB 계열의 MAB 알고리즘을 사용하는 것이 대규모 비선형 함수의 전역 최적해를 탐색 성능 향상에 중요하게 기여할 수 있음을 확인하였다.
또한, 복잡한 상호종속성을 갖는 대규모 비선형 함수일수록, UCB 계열의 MAB 알고리즘을 사용하여 부분 문제를 선택하는 전략이 실제 최적해 탐색 성능을 효과적으로 향상시킬 수 있음을 실험적으로 확인하였다.
Ⅴ. 결 론
본 논문에서는 비선형 함수의 전역 최적화를 위한 대규모 협력 공진화 알고리즘에서 부분 문제의 선택을 위한 방법으로 MAB 알고리즘을 사용하는 방법을 제안하였다. 협력 공진화 알고리즘에서 다루어지는 비선형 최적화 문제는 하나 이상의 독립적인 부분 문제로 분할되며, 각각의 부분 문제는 목적 함수의 형태에 따라 적합도 향상에 상이한 기여도를 갖는다. 이에 따라, 본 논문에서는 협력 공진화 알고리즘에서 각 부분 문제의 적합도 향상에 대한 기여도를 측정하고, MAB 알고리즘을 이용하여 각 시점에서 해 탐색을 수행할 부분 문제를 적응적으로 선택하는 “MAB 기반의 부분 문제 선택 방법”과 이에 기반한 MAB 기반의 협력 공진화 알고리즘인 “MABCC 알고리즘”을 개발하였다.
본 논문에서 제안한 방법의 최적해 탐색 성능을 평가하기 위한 실험에서 UCB 계열의 MAB 알고리즘, 특히 UCB1-Tuned 알고리즘을 사용하여 부분 문제를 선택할 때 협력 공진화 알고리즘의 최적해 탐색 성능이 크게 향상될 수 있음을 발견하였다. 또한 기존의 전통적인 협력 공진화 알고리즘과의 비교 실험에서도 본 논문에서 제안하는 방법이 가장 좋은 최적해 탐색 성능을 가짐을 확인하였다.
본 논문에서 제안한 방법은 기존의 전통적인 협력 공진화 알고리즘에서 부분 문제를 선택하는 과정이 전형적인 MAB 문제로 모델링될 수 있음을 확인하고, 협력 공진화 알고리즘에서 해 탐색 성능을 강화하는 데 효과적인 MAB 알고리즘을 발견하였다는 점에서 의의가 있다. 그뿐만 아니라, 부분 문제 선택 시 전통적인 기여도 기반의 방법으로는 해결하기 어려웠던 탐색과 활용의 균형을 MAB 알고리즘의 적용을 통해서 달성하고, 그 결과 해의 조기 수렴 및 해 탐색 속도의 저하 문제를 동시에 해결할 수 있음을 실험적으로 입증하였다는 점 또한 중요한 의의를 갖는다.
후속 연구에서는 본 논문에서 제안한 방법을 더욱 확장하여, 3.2 절에서 설명한 부분 문제의 기여도를 평가하는 방법과 3.3 절의 MAB 기반의 부분 문제 선택 방법을 더욱 고도화하는 연구를 수행하고, 다양한 MAB 알고리즘과 진화 알고리즘을 적용하여 성능 평가를 진행할 예정이다.
Acknowledgments
이 연구는 국립금오공과대학교 대학 연구과제비로 지원되었음(2022~2023)
References
-
M. N. Omidvar, X. Li, Y. Mei, and X. Yao, "Cooperative Co-Evolution With Differential Grouping for Large Scale Optimization", IEEE Transactions on Evolutionary Computation, Vol. 18, No. 3, pp. 378-393, Sep. 2014.
[https://doi.org/10.1109/TEVC.2013.2281543]

-
J.-Y. Song, K.-B. Lee, and J. Jang, "A Relief Method to Obtain the Solution of Optimal Problems", The Journal of IIBC, Vol. 20, No. 1, pp. 155-161, Feb. 2020.
[https://doi.org/10.7236/JIIBC.2020.20.1.155]

-
T. Kang, "A Compact Genetic Algorithm for Neural Networks Training", The Journal of KIIT, Vol. 18, No. 2, pp. 9-15, Feb. 2020.
[https://doi.org/10.14801/jkiit.2020.18.2.9]

-
W. Jeon, Y.-W. Ko, and J. Kim, "A Study of Nurse Scheduling Problem Using Efficient Approximation Algorithms", The Journal of KIIT, Vol. 14, No. 2, pp. 159-166, Feb. 2016.
[https://doi.org/10.14801/jkiit.2016.14.2.159]

- J.-U. Chang and C.-H. Lin, "An Iterative Data-Flow Optimal Scheduling Algorithm based on Genetic Algorithm for High-Performance Multiprocessor", The Journal of IIBC, Vol. 15, No. 6, pp. 115-121, Dec. 2015. https://dx.doi.org/10.7236/JIIBC.2015.15.6.115.
-
V. Chandra and A. H. S, "Nature Inspired Meta Heuristic Algorithms for Optimization Problems", Computing, Vol. 104, No. 2, pp. 251-269, Feb. 2022.
[https://doi.org/10.1007/s00607-021-00955-5]

-
M. A. Potter and K. A. D. Jong, "A Cooperative Coevolutionary Approach to Function Optimization", Parallel Problem Solving from Nature — Lecture Notes in Computer Science, Vol 866, pp. 249-257, Oct. 1994.
[https://doi.org/10.1007/3-540-58484-6_269]

-
A. Slowik and H. Kwasnicka, "Evolutionary Algorithms and Their Applications to Engineering Problems", Neural Computing and Applications, Vol. 32, pp. 12363-12379, Mar. 2020.
[https://doi.org/10.1007/s00521-020-04832-8]

-
X. Ma, X. Li, Q. Zhang, K. Tang, Z. Liang, W. Xie, and Z. Zhu, "A Survey on Cooperative Co-Evolutionary Algorithms", IEEE Transactions on Evolutionary Computation, Vol. 23, No. 3, pp. 421-441, Jun. 2019.
[https://doi.org/10.1109/TEVC.2018.2868770]

-
Y. Mei, M. N. Omidvar, X. Li, and X. Yao, "A Competitive Divide-and-Conquer Algorithm for Unconstrained Large-Scale Black-Box Optimization", ACM Transactions on Mathematical Software, Vol. 42, No. 2, pp. 1-24, Jun. 2016.
[https://doi.org/10.1145/2791291]

-
K. S. Kim and Y. S. Choi, "An Efficient Variable Interdependency-Identification and Decomposition by Minimizing Redundant Computations for Large-scale Global Optimization", Information Sciences, Vol. 513, pp. 289-323, Mar. 2020.
[https://doi.org/10.1016/j.ins.2019.10.049]

-
A. Slivkins, "Introduction to Multi-Armed Bandits", Foundations and Trends in Machine Learning, Vol. 12, No. 1-2, pp. 1-286, Nov. 2019.
[https://doi.org/10.1561/2200000068]

-
P. Auer, N. Cesa-Bianchi, and P. Fischer, "Finite-time Analysis of the Multiarmed Bandit Problem", Machine Learning, Vol. 47, pp. 235-256, May 2002.
[https://doi.org/10.1023/A:1013689704352]

-
G. Tabei, Y. Ito, T. Kimura, and K. Hirata, "Design of Multi-Armed Bandit-Based Routing for in-Network Caching", IEEE Access, Vol. 11, pp. 82584-82600, Aug. 2023.
[https://doi.org/10.1109/ACCESS.2023.3301961]

-
X. A. F. Cabezas, D. P. M. Osorio, and M. Juntti, "A Multi-Armed Bandit Framework for Efficient UAV-Based Cooperative Jamming Coverage", IEEE Transactions on Vehicular Technology, Vol. 72, No. 12, pp. 16893-16898, Dec. 2023.
[https://doi.org/10.1109/TVT.2023.3299670]

- K. Tang, P. N. Suganthan, Z. Yang, and T. Weise, "Benchmark Functions for the CEC'2010 Special Session and Competition on Large Scale Global Optimization", Technical Report, Nature Inspired Computation and Applications Laboratory, USTC, China, Nanyang Technological University, pp. 1-18, Nov. 2009.
- https://www.sfu.ca/~ssurjano/optimization.html, [accessed: Feb. 20, 2024]
-
R. Storn and K. Price, "Differential Evolution - A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces", Journal of Global Optimization, Vol. 11, pp. 341-359, Dec. 1997.
[https://doi.org/10.1023/A:1008202821328]

-
B. Kazimipour, M. N. Omidvar, A. K. Qin, X. Li, and X. Yao, "Bandit-based Cooperative Coevolution for Tackling Contribution Imbalance in Large-scale Optimization Problems", Applied Soft Computing, Vol. 76, pp. 265-281, Mar. 2019.
[https://doi.org/10.1016/j.asoc.2018.12.007]

-
M. N. Omidvar, X. Li, and X. Yao, "Smart Use of Computational Resources based on Contribution for Cooperative Co-evolutionary Algorithms", Proc. of the 13th Annual Conference on Genetic and Evolutionary Computation, Association for Computing Machinery, pp. 1115-1122, Jul. 2011.
[https://doi.org/10.1145/2001576.2001727]


2011년 2월 : 국립목포대학교 사범대학 컴퓨터교육과(공학사)
2020년 8월 : 한양대학교 대학원 전자컴퓨터통신공학과(공학박사)
2020년 9월 ~ 2022년 2월 : 한양대학교 컴퓨테이셔널 사회과학 연구센터 박사후연구원(Post-Doc.)
2022년 3월 ~ 현재 : 국립금오공과대학교 컴퓨터공학과 교수
관심분야 : 인공지능, 기계학습, 계산지능이론, 최적화