시공간 데이터 학습을 이용한 딥러닝 모델 기반 교통사고 위험 예측
초록
교통사고 예측은 이를 통한 사전 예방 활동이 가능하다는 점에서 효용성이 높으나, 데이터의 불규칙성과 희소성이 높아 학습 난이도가 매우 높다. 본 연구는 교통사고 위험도 예측의 정확도를 높이기 위한 효율적인 딥러닝 모델과 시공간 데이터를 효과적으로 활용하는 방법을 제안한다. 제안하는 모델은 그리드 공간의 특징을 추출하기 위한 2D 컨볼루션 계층 블록, 시계열적 특성을 학습하기 위한 RNN 계층 블록과 함께 학습에 사용되는 특징 데이터와 학습된 특징 맵 사이의 연관성을 효과적으로 학습하기 위한 어텐션 블록을 가진다. 다른 모델과의 비교 평가에서 제안 모델은 적은 수의 학습 매개변수로 더 우수한 성능을 보여주었다. 또한 2차 가공 데이터 등 다양한 데이터를 학습 데이터로 활용하여 예측 성능을 향상시킬 수 있음을 보여주었다.
Abstract
Traffic accidents forecasting is highly useful because it enables prevention activities, but the high irregularity and sparsity of data make training very difficult. This study proposes an efficient deep learning model to improve the accuracy of traffic accident risk forecasting and a method to effectively utilize spatiotemporal data. The proposed model has a 2D convolutional layer block to extract features in grid space, an RNN layer block to learn time series characteristics, and an attentional block to effectively learn the association between the feature data used for training and the learned feature map In the comparative evaluation with other models, the proposed model showed better performance with fewer learning parameters. We have also shown that various data, including secondary processing data, can be utilized as training data to improve prediction performance.
Keywords:
traffic accident forecasting, deep learning, spatiotemporal data, attention block, time-series data estimationⅠ. 서 론
시계열 데이터는 동일한 형태의 자료를 일정 시간 간격으로 반복 수집하여 구성한 데이터로 수치 정보로부터 텍스트, 음성 및 영상 정보에 이르기까지 실생활에서 얻을 수 있는 다양한 자료로 구성될 수 있다. 시계열 데이터에는 시간적 흐름에 따른 자료의 동적인 변화에 대한 정보가 존재하므로 이러한 특징을 파악하기 위한 다양한 연구가 수행되었다. 특히, 딥러닝 기술의 발달은 시계열 데이터를 특정 범주로 분류하거나[1] 비정상적 상황을 탐지(Anomaly detection)하고[2] 미래의 정보를 예측할 뿐 아니라[3] 새로운 시계열 데이터를 생성하는[4] 등 시계열 데이터 분석의 영역을 확대하고 정확성을 높이는 데 크게 기여하였다. LSTM(Long-Short Term Memory)과 같은 RNN(Recurrent Neural Networks) 모델은 ARMA(Auto-Regressive Moving Average)나 ARIMA(Auto-Regressive Integrated Moving Average)와 같은 통계적 분석 모델보다 시계열 내 비선형 패턴이나 동적으로 변화하는 패턴을 파악하는 데 유리하며 메모리 셀을 통해 시계열 내의 장기 연관 정보를 추출할 수 있어서 시계열 데이터 예측에 널리 사용되고 있다.
이러한 연구 성과에도 불구하고 시계열 데이터 예측은 여러 가지 어려움으로 인해 아직 도전적인 연구 분야라 할 수 있다. 시계열 데이터에는 상당한 무작위성(Randomness)이 내포되어 있을 수 있고, 이는 노이즈와 같은 역할을 하여 예측을 어렵게 만들며, 많은 변수를 포함하는 다변량 시계열일 경우 상호 연관성을 갖는 변수를 특정하거나 수집하기가 어려울 수 있다. 학습 데이터의 너무 적거나 너무 많은 경우와 같이 다양한 데이터의 특성과 수집 환경에 따라 최적의 학습 모델을 찾거나 구축하는 것이 쉽지 않으며 모델의 성능이 하이퍼파라미터의 값에 민감하게 변할 수 있다. 또한 실시간 시계열 예측의 효용성을 높이기 위해서는 예측에 따른 사전 대응 시간 확보를 위해 장시간(Multi-horizon)의 예측이 필요한데 예측 시간이 길어질수록 예측 정확도가 하락할 수 있다.
많은 시계열 데이터가 실제 생활 공간에서 발생하므로 시계열 데이터는 공간 또는 지리적인 연관성을 갖는 시공간적(Spatio-temporal) 시계열 데이터가 될 수 있다. 즉, 시공간적 시계열 데이터에서는 개별 공간에 독자적인 시계열 데이터가 존재하지만, 데이터들은 공간적으로 상호 연관성을 가질 수 있다. 따라서 시공간적 시계열 데이터 학습 모델은 시계열에서의 연관성뿐만 아니라 공간적 연관성도 추출할 수 있어야 한다. 교통 데이터, 환경 데이터, 설비 센서 및 제어 데이터 등은 잘 알려진 시공간적 시계열 데이터이다. 시공간적 시계열 데이터 예측에서는 각 공간의 시계열 데이터를 함께 예측해야 하는데 시계열 데이터 간의 불균형성으로 인해 데이터의 불규칙성이 증가해 예측 난이도가 더욱 증가하게 된다. 교통 데이터 중 각 도로의 교통량(Traffic flow)을 예측하는 문제는 공간적으로 연결된 도로의 교통량 사이에 높은 연관성이 있으며 단위 시간에서의 통행 차량 수가 적지 않고 시간적 규칙성이 높으므로 학습이 비교적 용이한 편이다. 반면 교통사고 예측의 경우, 교통량뿐 아니라 날씨, 유동 인구, 부주의 운전 등 다양한 요인에 의해 발생하므로 데이터의 불규칙성이 높고 낮은 발생 빈도에 따른 높은 희소성(Sparsity)으로 인해 정밀도(Precision)와 재현율(Recall) 측면에서 우수한 예측 성능을 확보하기가 매우 어렵다.
최근 제안되고 있는 교통사고 예측을 위한 딥러닝 모델에서는 시간적 특성의 학습을 위해 RNN 또는 Transformer[5][6]가, 공간적 특성의 학습을 위해서는 CNN(Convolutional Neural Networks)과 GNNs(Graph Neural Networks)이 주로 사용되고 있다[7][8]. 지리적 공간을 격자 그리드로 나누어 시계열 데이터를 수집하는 경우, CNN이 사용에 적합한데 실제 도로는 격자 형태가 아니므로 격자 구조 데이터는 실제 공간의 양자화로 인한 오차를 가지게 된다. 즉, 도로망을 기준으로 한 데이터를 학습하기 위해서는 그래프 기반의 GNN이 적합하지만, 반면에 그래프 데이터의 수집이 쉽지 않고 GNN의 학습 성능이 제한적일 수 있는 문제가 있다.
본 논문은 교통사고의 위험도 예측의 정확도를 높이기 위해 시계열 및 공간 데이터를 효과적으로 활용하고 최적의 학습 모델을 구축하는 방법을 연구한다.
현재 우수한 성능을 보여주는 시공간적 시계열 데이터 학습 모델들을 대상으로 사용하고 있는 핵심 모듈의 효과를 분석하고 효율적인 학습 데이터 구성 방법을 탐구하여 교통사고 위험도 예측 성능을 높이기 위한 최적의 모델과 데이터를 제시한다.
본 논문의 구성은 다음과 같다. Ⅱ장에서는 시공간 데이터를 기반으로 한 최신 교통사고 위험 예측 모델에 대해 모델의 특징과 데이터 사용 방법에 대해 살펴본다. Ⅲ장에서는 교통사고 위험 예측을 위한 효과적인 학습 모델과 시공간 학습 데이터 구성 방법을 제시한다. Ⅳ장에서는 제안 방법의 성능을 평가하기 위한 데이터셋 및 평가지표와 함께 다양한 비교 평가 결과를 제시하며, 마지막 Ⅴ장에서 결론 및 향후 과제에 대하여 기술한다.
Ⅱ. 관련 연구
교통사고 발생 가능성이 높은 장소와 시간대를 사전에 파악할 수 있다면 사고 위험도를 낮추기 위해 순찰을 강화하거나 교통 통제를 하는 등의 예방 활동이 가능하므로 교통사고 예측은 효용성이 높은 연구 주제이다. 반면 교통사고 데이터는 희소성과 불규칙성이 높은 이산적인(Discrete) 특성을 가지므로 학습 난이도가 높아 실효성있는 예측 성능을 가지는 모델 개발이 쉽지 않다. 이러한 문제를 해결하기 위해 최근 여러 분야에서 우수한 성능을 보여주는 Transformer 또는 그래프 학습이 가능한 GNN을 채택하는 모델이 늘어나고 있다.
Hetero-ConvLSTM[9]은 ConvLSTM(Convolutional Long-Short Time Memory)[10]에 기반한 모델로 1일 단위로 5km×5km 크기의 그리드 셀에 대한 교통사고 수를 예측하는 데 사용되었다. ConvLSTM은 시공간 예측 문제를 처리하기 위한 LSTM의 변형 모델로 LSTM의 앞단에 컨볼루션 계층을 추가하여 그리드 데이터의 공간적 특징을 추출하여 LSTM 셀로 전달한다. Hetero-ConvLSTM 모델은 사고 발생 패턴이 지역적으로 다르게 나타나는 공간적 이질성(Spatial heterogeneity)의 요인을 파악하기 위해 도로 사이에 공간 그래프를 구성하고 고유 분석(Eigen-analysis)[11]을 수행하였다. 이를 기반으로 스펙트랄 클러스터링(Spectral clustering)[12]을 수행하고 이 정보를 그리드에 대응시켜 그리드에 공간적 특징을 부여한다. 또한 공간적 이질성 문제로 인한 예측 불안정성을 극복하기 위해 ConvLSTM 모델 적용 시 전체 그리드 공간을 50% 겹침을 사용하는 하위 창으로 나누어 예측을 수행하고, 겹치는 지역의 예측을 앙상블하여 최종 예측을 산출한다.
STCL-Net(SpatioTemporal Convolutional Long short-term memory Network)[5] 모델은 인구, 토지 사용, 도로망과 같은 지리적 정보는 CNN 계층으로, 날씨와 같은 시계열 환경 정보는 LSTM 계층으로, 교통사고 정보와 택시 승하차 정보는 ConvLSTM 계층으로 특징을 추출하고 이를 병합하여 예측을 수행하는 모델이다. 동일한 지역에 대해 그리드 셀의 크기를 다르게 하여 1주, 1일, 1시간 후의 교통사고 위험을 각각 예측하도록 하여 예측 성능을 비교한 결과는 예상대로 그리드 셀의 크기와 예측 시간 단위가 작아질수록 데이터의 희소도가 높아져 급격히 예측 성능이 감소하였다.
GSNet[7] 모델은 그리드 기반 시공간 지리적 모듈과 그래프 기반 시공간 의미 모듈을 결합시킨 모델이다. 그리드 기반 시공간 지리적 모듈은 컨볼루션 계층 및 GRU(Gated Recurrent Unit) 계층 이후에 어텐션 네트워크를 추가하여 예측을 위한 특징 학습이 용이하도록 구성되었다. 그래프 기반 시공간 의미 모듈은 위험도, 도로, 관심 지점(PoI, Points of Interests) 등을 노드로 하여 그래프를 생성하고 이를 GCN(Graph Comvolution Networks)을 이용해 특징을 추출한 다음 GRU 계층 및 어텐션 네트워크를 통과시켜 얻어진 결과를 그리드로 대응시킨다. 또한 위험도가 높은 경우의 학습을 강화하기 위해 위험도에 따른 가중치를 사용하는 WMSE(Weighted Mean Square Error)를 손실함수로 사용하였다. 학습 데이터 측면에서는 교통사고의 시간적 주기성을 분석해 단기적 유사성과 장기적 주기성을 확인하고 이를 바탕으로 학습을 위한 시계열 데이터를 구성하였다.
TWCCnet[8] 모델과 MVMT-STN[13] 모델은 GSNet의 성능을 개선한 모델이다. TWCCnet 모델에서는 GSNet 모델의 지리적 모듈과 그래프 모듈에 사용된 계층의 성능을 평가하여 기존 GRU 계층을 양방향 GRU 계층으로 변경하는 등의 최적화가 이루어졌다.
MVMT-STN 모델은 셀 크기가 작은 그리드와 2배의 크기를 갖는 그리드에 대한 모델을 동시에 학습하고 두 모델이 동일 그리드에 대해 예측하는 값이 일치하도록 하는 제약조건을 손실함수에 추가로 사용하였다. 이를 통해 셀 크기가 작은 그리드에서 데이터 희소성 문제로 예측 성능이 낮아지는 문제를 큰 셀의 그리드 데이터 학습을 이용해 완화시키고자 하였다.
참고로, TFT(Temporal Fusion Transformer)[14] 모델은 구글에서 제안한 시계열 예측 모델로 다변수 시계열 데이터와 정적 및 동적 변수, 관찰 변수 및 사전 인지 변수 등 이종(Heterogeneous) 데이터를 효과적으로 학습하여 예측 대상 변수의 다중 시간 예측(Multi-horizon forecasting) 성능을 향상한 모델이다. TFT 모델은 내부 Transformer 기반의 셀프 어텐션 네트워크를 통해 각 시계열 데이터 및 변수 사이의 단기 연관성을 추출하고 LSTM 인코더를 통해 시계열 데이터 및 변수의 장기적 특성을 추출하는 구조로 되어 있다. 다만 시계열의 공간적 특성은 고려되지 않기 때문에 시공간적 시계열 데이터를 학습하는 데에는 최적화되어 있지 않은 단점이 있다.
Ⅲ. 제안 기법
3.1 접근 방법
교통사고 위험 예측을 위한 모델 설계를 위해 기존 모델들을 분석하고 성능을 평가하였다. 평가 결과, 그래프 기반의 공간적 특징을 학습하기 위해 GNN을 사용하고 있는 모델들도 대부분 그리드 데이터 학습을 위해 CNN을 함께 사용하고 있는데, 실제 그래프 학습을 통해 추가로 얻을 수 있는 성능 향상의 폭이 매우 제한적임을 알 수 있었다. 이는 그래프 모델 학습에 사용되는 데이터가 충분치 않은 경우가 많고, 교통량과 달리 교통사고는 불연속적이고 불규칙적으로 발생하므로 주위 노드와의 정보 교환이 크게 영향을 미치지 못하기 때문이라고 판단된다. 실제로 교통사고 및 연관데이터는 GPS 좌표로 기록되는 경우가 많고 아직 도로망 등에 대한 그래프 정보가 부족한 상황이라 그래프 기반 모델을 통한 성능 향상을 기대하기가 쉽지 않다.
본 연구에서는 이러한 분석을 기반으로 그래프 모델을 사용하지 않고 그리드 데이터만 학습하여 교통사고를 예측하는 모델을 설계하되, 학습에 도움이 될 수 있는 시공간 데이터를 추가로 사용하여 예측 성능을 높이고자 한다.
3.2 학습 모델
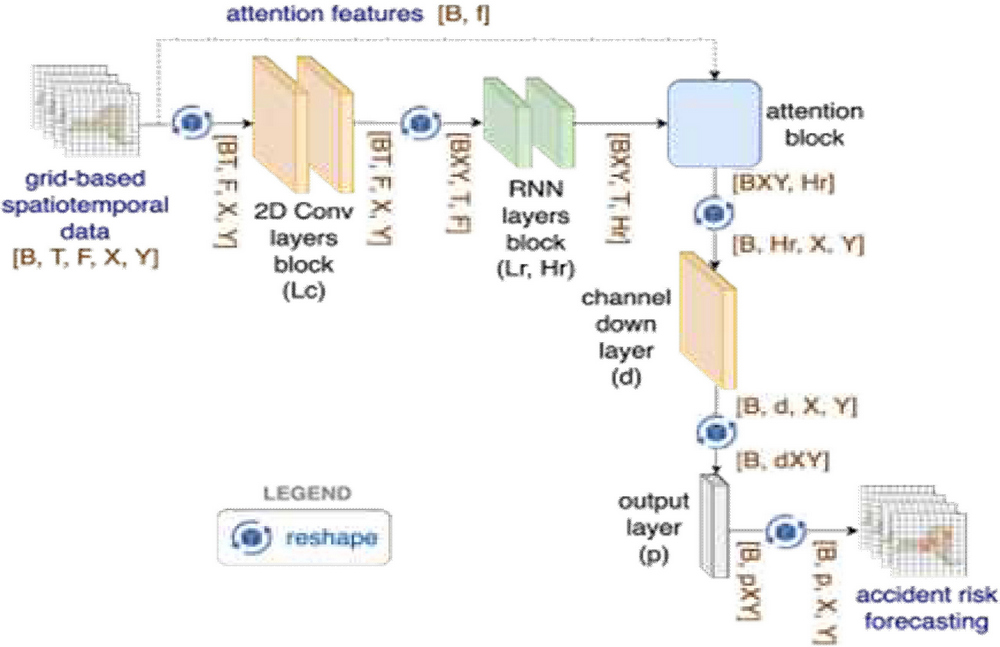
제안하는 모델은 그리드 기반 시공간 데이터를 학습하여 교통사고 위험도를 예측하는 모델로 그리드 공간의 특징을 추출하기 위한 2D(Two dimensional) 컨볼루션 계층 블록과 시계열적 특성을 학습하기 위한 RNN 계층 블록 및 학습에 사용되는 특징 데이터와 학습된 특징 맵 사이의 연관성을 효과적으로 학습하기 위한 어텐션 블록을 중심으로 한다. 제안하는 모델의 구조는 그림 1과 같다.
그리드 기반 시공간 데이터는 가로, 세로 셀의 개수가 X, Y인 그리드에 대해, 학습에 사용되는 F 개의 특징 데이터를 시계열화한 것이다. 제안 모델은 배치 크기 B의 T 개 시간 시퀀스([B, T, F, X, Y])를 학습하여, 향후 p 스텝 시간 동안의 교통사고 위험도([B, p, X, Y])를 예측하도록 구성하였다. 2D 컨볼루션 계층 블록(그림 1의 2D Conv layers block)은 Lc 개의 2D 컨볼루션 계층으로 구성되어 그리드 데이터에서 공간적 특징을 학습하고 입력과 동일한 모양([BT, F, X, Y])의 특징 맵을 출력한다. 이 데이터는 RNN 학습을 위한 형태로 변형([BXY, T, F])되어 RNN 계층 블록(그림 1의 RNN layers block)에 전달된다. RNN 계층 블록은 Lr 개의 계층과 Hr 개의 내부 노드(Hidden size)를 갖는 Stacked RNN 구조를 가지며 내부 노드에서 시계열 특징 데이터에 존재하는 시간적 특징을 학습하여 그 결과를 출력한다. RNN 모델로는 LSTM과 GRU를 사용할 수 있는데, 최근의 시계열 예측 모델에서는 대체로 GRU가 LSTM보다 좀 더 나은 성능을 보여주고 있다[8].
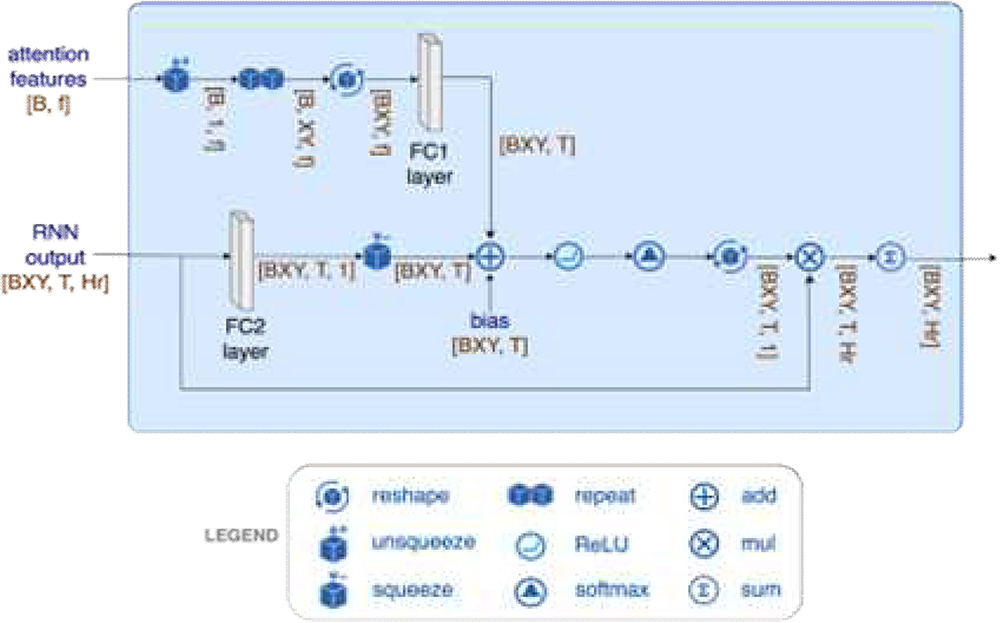
어텐션 블록은 T 시간 시퀀스의 RNN 출력 맵([BXY, T, Hr])과 예측 시점에서의 f개(f≤F) 특징 데이터([B, f])를 입력받아 특징 데이터가 예측 결과에 기여하는 정도를 학습하고 이를 RNN 출력 맵에 반영한 결과를 내보낸다. 어텐션 블록의 상세 내부 구조는 그림 2와 같다.
어텐션 블록의 완전연결(fully-connected) 계층 FC1을 통해 f 개의 특징을 각각 얼마나 예측에 반영할지를 학습하고, 완전연결 계층 FC2를 통해 RNN의 각 노드 출력의 예측 반영 중요도를 학습한다. FC1과 FC2 계층의 출력은 ReLU 및 Softmax 함수를 통해 어텐션 점수로 계산되며 이 점수가 RNN 출력 맵에 가중치를 부여하여 예측 값 결정에 사용된다. 어텐션 점수 α는 식 (1)과 같이 계산된다. 이 식에서 WFC1과 WFC2는 각각 FC1, FC2 계층의 가중치를, b는 바이어스를 의미하고, Hr과 f *은 RNN의 내부 노드 상태와 예측 시점의 특징 데이터를 의미한다.
| (1) |
어텐션 블록의 출력([BXY, T, Hr])을 각 그리드 셀의 출력 형태([B, Hr, X, Y])로 변형(Reshape)하면 다음에 1×1 컨볼루션 계층 또는 완전연결 계층을 하나만 사용하여 각 그리드 셀의 예측값([B, p, X, Y])을 얻어낼 수 있다. 전자의 경우 학습 매개변수 수를 최소화할 수 있는 장점이 있지만 적은 매개변수로 인해 학습 성능이 다소 저하되는 경우가 발생하고, 완전연결 계층만을 이용하면 매개변수가 너무 많아져 도리어 학습이 어려워지는 문제가 발생하게 된다.
이에 제안 모델에서는 먼저 1×1 컨볼루션 계층(그림 1의 channel down layer)을 사용하여 채널 수를 Hr에서 d로 줄인 후 완전연결 계층(그림 1의 channel down layer)을 사용하여 예측 출력을 얻어내도록 설계하였다.
3.3 시공간 정보 활용 방법
정확한 교통사고 위험도 예측을 위해 교통사고와 연관성이 있다고 판단되는 다양한 정보가 시공간 특징 정보로 학습에 활용된다. 즉, 운전에 영향을 미칠 수 있는 요일, 휴일, 혼잡시간 등의 시간 정보, 날씨 정보, 교통량 정보, 유동인구 정보, 행사 정보, 주변 건물 정보, 사고 위험 지역 정보 등을 특징 정보로 활용할 수 있다. 학습을 위해 확보할 수 있는 데이터는 일반적으로 제한되어 있으므로 가용 데이터를 학습에 어떻게 활용해야 하는지를 결정해야 한다.
먼저 가용 데이터 중 어떤 데이터를 학습에 사용할지 결정해야 한다. 가능한 데이터를 모두 사용하는 것이 좋을 수 있지만 관련성이 낮은 데이터를 사용하면 도리어 학습 용이성을 떨어뜨릴 수 있기 때문이다.
다음으로 데이터를 어떤 형식으로 또는 어떤 값으로 학습에 활용할지를 생각할 필요가 있다. 시간 데이터 중 시(hour) 정보, 요일 정보, 월 정보 등은 카테고리 데이터 또는 수치 데이터로 사용할 수 있다. 또한, 학습 데이터가 부족하거나 희소성이 높을 때 기존 데이터를 가공한 2차 데이터를 사용할 수 있다. 교통사고 데이터의 경우 한 그리드 셀의 데이터가 희소할 경우 인접 셀과의 합산 데이터를 추가적인 데이터로 학습에 활용해 볼 수 있다.
어텐션 계산에 사용되는 특징 데이터는 예측 시점의 데이터이므로 정적 또는 사전 인지 데이터만 사용할 수 있다. 여기에 해당하는 데이터 중에서 어떤 것을 어텐션 블록에 사용할지도 결정 대상이 된다.
학습에 들어가는 시퀀스 시간 수 T와 시간 값을 결정하는 것도 필요하다. 보통 예측 단위와 동일한 시간 간격으로 학습 시계열 데이터를 생성하는데 시계열 데이터의 주기성을 고려하여 이전 1주에서 1개월 정도의 데이터를 학습에 활용한다. 만약 예측 단위가 1시간이고 이전 1개월 데이터를 학습에 사용하면 한번에 672 스텝 시간의 시퀀스 데이터를 학습해야 하므로 모델의 크기가 너무 커져 자원이 충분하지 않으면 학습에 문제가 생길 수 있다. 이때 학습에 도움이 되는 시간대의 데이터만으로 학습 시계열 데이터를 구성해서 학습 효율을 높일 수 있다. 즉, 최근 몇 시간 데이터와 동일 요일의 동일 시간대의 이전 데이터를 결합하여 학습 시퀀스로 사용할 수 있다. 한 번에 전체 그리드 데이터를 학습해야 하므로 배치 크기 역시 학습 데이터의 크기에 따라 조절해야 한다.
Ⅳ. 성능 평가
4.1 데이터셋
교통사고 위험 예측을 위해서는 실제 도시의 교통사고 관련 데이터를 수집하여 학습해야 한다. 우리나라의 공공데이터포털[15]과 소방안전 빅데이터 플랫폼[16]에도 관련 데이터가 다수 탑재되어 있으나 해당 데이터를 이용한 교통사고 예측 연구 결과가 거의 없어 이전 연구와의 예측 성능 비교가 어려운 문제가 있다. 따라서 본 연구에서는 다수의 모델에서 학습 데이터로 사용한 미국의 뉴욕(New York city)과 시카고(Chicago)의 교통사고 데이터를 학습 데이터로 사용하였다[7][8]13].
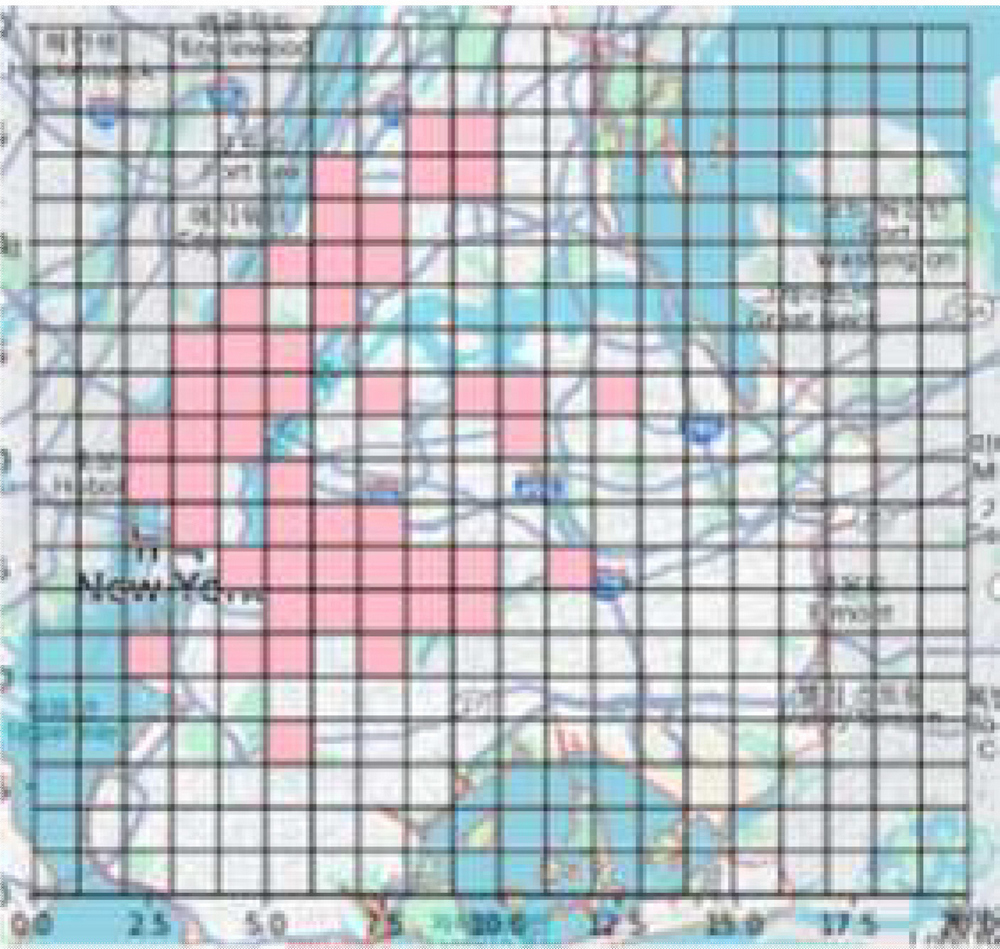
뉴욕과 시카고의 교통사고 데이터는 두 도시를 가로, 세로 각각 20개로 영역으로 나눈 그리드 데이터를 구성하였다. 각 그리드 셀은 2km×2km의 크기를 가지며 도시의 모양으로 인해 총 400개의 셀 중 데이터가 없는 셀이 다수 존재한다. 그림 3은 뉴욕 데이터셋의 그리드 설정을 보여준다. 분홍색으로 표시된 셀은 차량의 통행량이 많은 지역으로 사고 발생 빈도가 상대적으로 높은 지역이다. 해당 사고 위험 셀의 수는 뉴욕 및 시카고에 각각 50개씩 지정되어 있다.
데이터셋에는 1시간 단위로 각 그리드 셀의 교통사고 정보(위험지수), 날씨 정보(기온, 구름상태, 비, 눈, 안개 여부), 관심지점(PoI, Points of Interests) 수(교육시설,문화시설, 교통시설, 상업시설 등) 및 교통량 정보(택시 승하차 수) 등이 들어있다. 데이터셋의 세부 정보는 표 1과 같다.
예측 대상은 각 셀의 시간별 교통사고 위험지수이다. 교통사고 위험지수는 각 교통사고의 위험 정도에 따라 경미한 사고에 1점, 부상 사고에 2점, 사망 사고에 3점을 부여하고 이를 해당 시간 사고에 대해 합산한 수이다. 교통사고 수 대신 위험지수를 사용하면 데이터 희소성을 경감시키고 위험도가 높은 교통사고에 대한 예측 성능이 높일 수 있는 장점이 있다.
4.2 평가지표 및 평가 방법
교통사고 위험도 예측 모델의 성능을 평가하기 위해 RMSE(Root Mean Square Error), Recall(재현율), MAP(Mean Average Precision)의 세 가지 평가지표를 사용한다. RMSE는 위험지수 예측의 정확도를 보여주고, Recall은 실제 교통사고를 예측한 비율, MAP은 예측한 교통사고 중 실제 발생한 평균 비율을 의미한다. 두 도시의 400개의 셀 중 실제 교통사고 데이터가 존재하는 셀도 통행량이 적어 교통사고 발생이 매우 적은 곳은 예측이 매우 어려울 뿐 아니라 전체 평가지표 값을 왜곡할 수 있으므로 두 도시 모두 교통사고 발생 건수가 많은 50개의 셀로 평가 대상을 제한하였다. 평가지표 RMSE, Recall, MAP를 계산하는 방법은 각각 식 (2)~(4)와 같다.
| (2) |
| (3) |
| (4) |
Yc,t와 는 각각 셀 c의 시점 t에서의 실제 및 예측 위험지수이고, C는 평가에 사용되는 셀 수, T는 전체 예측 시점 수를 의미한다. Rt는 시점 t에서 발생하는 교통사고의 위치 셀의 집합이고 Zt는 시점 t에서 높은 위험도로 예측된 셀의 집합(단, |Zt| = |Rt|)이다. p(j)와 r(j)는 각각 Rt의 원소 셀 j의 정밀도와 재현율이다.
평가는 1시간을 단위로 t - 1 시점까지의 시계열 데이터를 학습하여 t 시점을 예측하는 단일스텝 예측과 t 시점부터 t + N - 1 시점까지 총 N 스텝 시간을 예측하는 다중스텝 예측으로 구성된다. 다중스텝 예측의 평가는 N 스텝 예측에 대해 각 스텝에서의 평가지표 값과 이 값들의 평균 및 표준편차이다.
4.3 데이터 전처리 및 학습 방법
뉴욕 데이터셋은 총 400개 셀 각각에 대해 32개의 원-핫 인코딩된 시간(24시간, 요일) 데이터, 7개의 관심 지점 데이터, 6개의 날씨 데이터, 2개의 교통량 데이터로 구성된 8,760 스텝 시간 데이터로 구성되어 있다. 시카고 데이터셋에는 관심 지점 데이터가 포함되어 있지 않다. 본 연구에서는 이외에 표 2에 나타난 관련 데이터를 추가로 학습에 활용하였다.
셀 좌표 및 숫자 인코딩 시간 정보는 시공간 정보의 연속성을 부여하기 위해 추가하였고, 확대 사고위험지수는 데이터의 희소성 완화를 위해 좌표 위치가 ±1인 인근 셀의 위험지수를 인접도에 따라 가중치를 두어 합산한 값이다.
그래프 기반 사고위험지수는 데이터셋에서 제공되는 위험도 그래프, 관심 지점 그래프, 도로 그래프에서 직접 연결된 셀의 위험지수를 합산한 값이다. 추가로 이 데이터들의 조합을 학습 데이터로 사용해 보았다.
학습, 검증, 시험용 데이터는 전체 데이터셋을6:2:2의 비율로 분할하여 사용하였다. 학습에 사용되는 시간 스텝 수는 최근 3시간 데이터와 최근 4주의 동일 요일 및 시간 데이터로 구성된 7 시퀀스 데이터를 기본으로 다양한 조합을 시험해 보았다. 배치 수는 약간의 실험을 통해 전체 그리드를 기준으로 16으로 정하였다.
학습 모델 및 학습 방법에 다양한 하이퍼파라미터가 존재한다. 학습 모델 구성시 Lc=2인 컨볼루션 계층 블록을 사용하였고, RNN 계층 블록은 Lr=5, Hr=256으로 설정하였으며, 채널다운 계층은 d=16을 기본으로 사용하였다. 어텐션 블록에 사용되는 특징 데이터는 데이터셋의 시간 데이터에 추가로 숫자 인코딩 시간 및 셀 좌표 등을 사용해 보았다. 학습을 위한 손실함수로는 일반적인 MSE(Mean Square Error)를 사용하였고, 옵티마이저(Optimizer)는 Adam, 학습률은 1e-5를 사용하였다.
4.4 평가 결과
성능 평가는 제안 모델의 다양한 설정에 따른 성능 비교, 다른 모델과의 비교 평가, 다중스텝 예측 성능 및 제거 연구(Ablation study)로 구성된다. 먼저 모델을 구성하는 각 블록의 규모에 따른 성능을 비교한 결과가 표 3에 요약되어 있다. 컨볼루션 계층 블록에서의 계층 수(Lc), RNN 계층 블록의 계층 수(Lr) 및 내부 노드 수(Hr), 채널 다운 계층의 출력 크기(d)를 달리하여 실험한 결과 RNN 계층 블록의 계층 수가 성능에 가장 영향을 주는 것으로 나타났으나 성능 차이는 크지 않았다. 이후 평가부터는 표 3의 첫 번째 설정 모델을 사용하였다.
표 4는 기본 데이터셋에 추가 데이터를 학습에 사용하였을 때의 성능 변화를 요약한 것이다. 원-핫 인코딩 기법의 시간 정보 외에 숫자 인코딩 방식의 시간 정보를 추가로 사용하였을 때 약간의 성능 향상을 보였다. 또한 숫자 인코딩 데이터를 어텐션 연산에 반영하는 것(+Tnum(att) 설정)도 어느 정도 학습에 도움을 주는 것으로 보였다. 공간과 관련된 정보 중에는 그래프 기반 사고위험지수(Rgrf)가 성능을 향상할 가능성이 있어 보인다. 다만 시카고 데이터셋에는 관심 지점 정보가 존재하지 않아서인지 성능 향상이 나타나지 않았다. 참고로 다른 데이터를 함께 사용하는 것은 성능 향상에 거의 도움이 되지 않았다. 이는 학습 데이터가 늘어나는 경우 학습 비용도 함께 커지기 때문으로 보인다.
표 5는 학습에 사용되는 데이터 시퀀스의 구성에 따른 성능을 비교한 결과이다. GSNet이나 TWCCnet 등의 모델에서 사용한 방식인 최근 3시간 및 동일 요일/시간 최근 4주 설정을 각각 일정 부분 증가시켜 시험한 결과 주간 데이터를 한 주 늘린 설정에서 큰 성능 향상을 보였다. 1달이 4주 반 정도로 구성되므로 예측 시점 이전 5주 데이터도 높은 연관성을 보이는 것으로 판단된다. 반면 최근 시간 데이터는 학습 데이터를 증가시켜도 성능 향상에 큰 영향을 주지는 않는 것으로 나타났다.
표 6은 제안 모델의 성능을 다른 모델과 비교 평가한 결과이다. 비교 평가 모델로는 동일 데이터와 평가지표를 사용한 GSNet과 TWCCnet 및 TFT 모델을 사용하였다. TFT 모델은 그리드 형태로 데이터를 사용하지 않으므로 400개의 셀 중 평가 대상인 50개에 해당하는 셀만을 추출하여 학습에 사용하였다. 먼저 RMSE 지표에서는 GSNet과 TWCCnet 모델의 성능이 다른 모델보다 낮게 나타났는데, 이는 두 모델이 높은 위험지수에 가중치를 두는 WMSE로 학습되어서 RMSE 지표에서는 수치가 상대적으로 낮게 나타난 것으로 보인다. 이를 감안하고 Recall과 MAP 지표 측면에서 평가할 때도 제안 모델이 다른 모델보다 좀 더 나은 성능을 보여주었다. 참고로 TFT 모델은 학습 데이터를 불연속적으로 구성하기 어려워 이전 1주일의 시간 데이터인 총 168 스텝 시간을 사용하였는데 Recall 및 MAP 성능이 다른 모델보다 낮게 나타났다. 이는 모델이 공간적 특성을 고려하지 못하고 긴 시퀀스의 데이터를 학습해야 하기 때문으로 판단된다. 비교 평가 결과는 제안 모델이 적은 수의 학습 매개변수로 더욱 우수한 성능을 보여주는 효율성이 높은 모델임을 보여준다.
표 7은 제안 모델의 향후 24시간 예측 성능을 다중스텝 예측 성능이 우수한 것으로 알려진 TFT 모델과 비교한 결과이다. TFT 모델의 성능지표 수치는 제안 모델보다 떨어지는데 수치의 표준편차는 제안 모델보다 좀 더 낮게 나타났다. TFT 모델이 좀 더 안정적으로 예측한다고 볼 수 있지만 표준편차의 절대적인 값으로 볼 때 두 모델 모두 예측 안정성이 높다고 할 수 있다.
표 8은 제거 연구로서 제안 모델을 구성하는 블록을 제거했을 때의 성능 변화를 보여준다. 가장 큰 영향을 주는 블록은 어텐션 블록으로 어텐션 블록을 제거하면 학습이 불안정해져서 최적해를 찾는 시간이 오래 걸리거나 종종 국소 해(local optima)에 빠져 성능이 크게 나빠지는 결과를 가져온다.
그림 4는 뉴욕시 데이터셋의 각 평가대상 셀에 대해 교통사고 위험지수 표준편차와 예측결과(RMSE)의 관계를 도시한 것으로 위험지수 표준편차와 예측의 RMSE가 거의 정비례하는 것을 볼 수 있다.
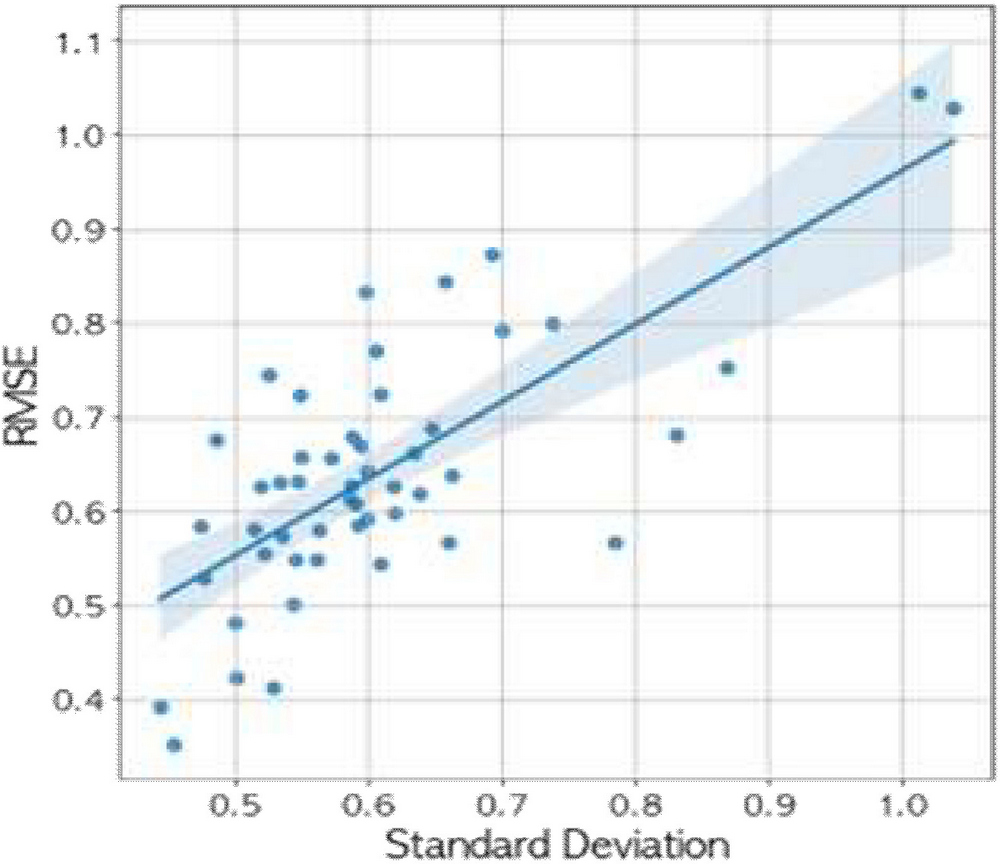
Relation between standard deviation of accidents risks and forecasting result (RMSE) for NYC target cells
시계열 데이터의 표준편차는 데이터의 변동성과 불확실성을 보여줄 수 있으며 이 결과를 통해 교통사고의 불규칙성이 높을 수록 예측이 더 어렵다는 것을 확인할 수 있다.
Ⅴ. 결론 및 향후 과제
본 논문은 비교적 적은 수의 매개변수 수를 가지면서도 우수한 예측 성능을 보여주는 효율적인 교통사고 위험도 예측 모델을 제안하였다. 또한 2차 가공 데이터 등 다양한 데이터를 추가 학습 데이터로 활용하여 예측 성능을 향상시킬 수 있음을 보여주었다.
제안 모델의 재현율은 뉴욕 데이터셋에서 약 35%로 전체 교통사고의 1/3 가량을 예측할 수 있는 수준이나 정밀도는 이보다 작은 20% 수준으로 위양성(False alarm) 비율이 높은 편이다. 확대 사고위험지수(Rexp)를 예측 목표로 하면 재현율과 정밀도는 각각 80%와 70% 수준까지 올라가는데 이는 데이터의 희소성과 이에 따른 불규칙성이 예측 성능과 직결되는 것을 보여준다. 시카고 데이터셋 학습 결과도 교통사고 빈도가 적고 학습을 위한 특징 데이터가 부족할 경우 예측 성능이 크게 떨어지는 것을 보여주고 있다. 따라서 실효성있는 예측 모델을 개발하기 위해서는 가능한 많은 관련 데이터를 확보하고 교통사고가 빈번히 발생하는 지역을 우선 예측 대상으로 정해야 한다.
만약 그래프 기반 학습 데이터가 충분히 많은 상황이라면 GNN을 사용한 모델의 학습 성능이 보다 향상될 수 있다. 향후 GNN을 효과적으로 활용할 수 있도록 제안 모델을 개선하는 연구를 수행할 예정이다. 또한 희소성이 높은 데이터를 보다 효과적으로 학습할 수 있는 어텐션 구조를 설계할 예정이다.
Acknowledgments
이 연구는 금오공과대학교 대학 학술연구비로 지원되었음(2021)
References
-
H. I. Fawaz, et al., "Deep learning for time series classification: a review", Data Mining and Knowledge Discovery, Vol. 33, pp. 917-963, Jul. 2019.
[https://doi.org/10.1007/s10618-019-00619-1]

-
Z. Z. Darban, G. I. Webb, S. Pan, C. C. Aggarwal, and M. Salehi, "Deep Learning for Time Series Anomaly Detection: A Survey", arXiv:2211.05244, [cs.LG], Nov. 2022.
[https://doi.org/10.48550/arXiv.2211.05244]

-
J. F. Torres, D. Hadjout, A. Sebaa, F. Martínez-Álvarez, and A. Troncoso, "Deep Learning for Time Series Forecasting: A Survey", Big Data, Vol. 9, No.1, pp. 3-21, Feb. 2021.
[https://doi.org/10.1089/big.2020.0159]

-
F. Gatta, F. Giampaolo, E. Prezioso, G. Mei, S. Cuomo, and F. Piccialli, "Neural networks generative models for time series", Journal of King Saud University - Computer and Information Sciences, Vol. 34, No. 10, Nov. 2022.
[https://doi.org/10.1016/j.jksuci.2022.07.010]

-
J. Bao, P. Liu, and S. V. Ukkusuri, "A spatiotemporal deep learning approach for citywide short-term crash risk prediction with multi-source data", Accident Analysis & Prevention, Vol. 122, pp. 239-254. Jan. 2019.
[https://doi.org/10.1016/j.aap.2018.10.015]

-
J. Grigsby, Z. Wang, N. Nguyen, and Y. Qi, "Long-Range Transformers for Dynamic Spatiotemporal Forecasting", arXiv:2109.12218, [cs. LG], Sep. 2019.
[https://doi.org/10.48550/arXiv.2109.12218]

-
B. Wang, Y. Lin, S. Guo, and H. Wan, "GSNet: Learning Spatial-Temporal Correlations from Geographical and Semantic Aspects for Traffic Accident Risk Forecasting", Proc. of the AAAI Conference on Artificial Intelligence, Vol. 35, No. 5, pp. 4402-4409, May 2021.
[https://doi.org/10.1609/aaai.v35i5.16566]

-
N. Bhardwaj, A. Pal, Bhumika, and D. Das, "Adaptive Context based Road Accident Risk Prediction using Spatio-temporal Deep Learning", IEEE Transactions on Artificial Intelligence, Vol. 1, No. 01, pp. 1-12, Aug. 2023.
[https://doi.org/10.1109/TAI.2023.3328578]

-
Z. Yuan, X. Zhou, and T. Yang, "Hetero-ConvLSTM: A Deep Learning Approach to Traffic Accident Prediction on Heterogeneous Spatio-Temporal Data", In Proc. of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD '18), pp. 984-992, Jul. 2018.
[https://doi.org/10.1145/3219819.3219922]

- X. SHI, Z. Chen, H. Wang, D.-Y. Yeung, W.-K. Wong, and W. Woo, "Convolutional LSTM network: A machine learning approach forr precipitation nowcasting", In Advances in neural information processing systems, Vol. 28, pp. 802-810, Dec. 2015.
- Wikipedia, "Eigenvalues and eigenvectors", https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors, [accessed: Feb. 22, 2024]
- Wikipedia, "Spectral clustering", https://en.wikipedia.org/wiki/Spectral_clustering, [accessed: Feb. 22, 2024]
-
S. Wang, J. Zhang, J. Li, H. Miao, and J. Cao, "Traffic Accident Risk Prediction via Multi-View Multi-Task Spatio-Temporal Networks", in IEEE Transactions on Knowledge & Data Engineering, Vol. 35, No. 12, pp. 12323-12336, Dec. 2023.
[https://doi.org/10.1109/TKDE.2021.3135621]

-
B. Lim, S. Zohren, and A. J. Smola, "Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting", International Journal of Forecasting, Vol. 37, No. 4, pp. 1748-1764, Oct. 2021.
[https://doi.org/10.1016/j.ijforecast.2021.03.012]

- Ministry of the Interior and Satefy, "Public Data Portal", https://www.data.go.kr/, [accessed: Feb. 22, 2024]
- National Fire Agency, "Fire safety big data platform", https://bigdata-119.kr/, [accessed: Feb. 22, 2024]

1995년 8월 : 연세대학교 전기전자공학과(공학석사)
2001년 2월 : 연세대학교 전기전자공학과(공학박사)
2002년 9월 ~ 현재 : 금오공과대학교 컴퓨터공학과, 인공지능공학과 교수
관심분야 : 머신러닝, 데이터분석, 스마트팩토리

2017년 3월 ~ 현재 : 금오공과대학교 수리빅데이터학과 학부과정
관심분야 : 머신러닝, 데이터분석