초음파 CDMA에서 도플러 효과에 강인한 처프-온오프 혼합 변조 방법

Ⅰ. 서 론

초음파를 이용한 송수신 장치는 자율주행자동차 및 무인 로봇 기술의 발달을 비롯한 여러 분야에서 사용량이 점차 늘고 있다[1]-[4]. 이런 송수신 장치는 공기를 매질로 높은 주파수의 음파를 송수신하여 주변 사물의 거리를 측정한다. 하지만 다수의 초음파 송수신 장치가 동시에 사용되는 경우 장치별 혼선이 발생한다. 이런 혼선은 거리 측정의 오차 및 검출 성능에 크게 영향을 준다[5]-[7].

초음파 장치 간의 혼선을 방지하기 위해 다중접속 방법(Multiple access)이 제안되었다. 시분할(Time division) 다중접속 방법은 장치별 사용 시간을 나눠 동 시간에 2개 이상의 초음파가 송신되지 않도록 하여 신호 간 직교성(Orthogonality)을 보장하는 방법이다[8]-[11]. 하지만 사용 시간 관리 장치의 필요성 및 측정 간격이 길어짐에 따라 잘 사용되지 않는다. 주파수 분할(Frequency division) 다중접속 방법은 장치별 사용 주파수를 나눠 신호 간 직교성을 보장하는 방법이다. 초음파 송수신 장치의 주파수 대역폭은 협대역 특징을 가진다. 따라서 주파수 분할을 위해 다수의 초음파 송수신 장치를 사용하거나 비싼 광대역 초음파 송수신 장치를 사용해야 하는 단점을 가진다. 코드 분할(Code division) 다중접속 방법은 ID 코드를 변조(Modulation), 복조(Demodulation) 과정을 통해 송수신하고 송신 신호의 코드와 수신 신호의 코드 간의 상호상관(Cross correlation)을 통하여 ID 코드를 감지하는 방법으로 신호 간 직교성을 보장한다[12]-[15]. 코드 변복조 과정에서 2개 이상의 초음파 신호가 수신된다면 파동의 상쇄보강간섭으로 인해 왜곡이 생겨 복조된 코드에 오차가 발생하므로 이를 보상하기 위해 ID 코드 수를 늘리게 되는 단점이 있다. 하지만 이런 단점에도 초음파 전파시간(Time of flight) 측정 정확도 향상 등 다른 장점이 많아 코드 분할 다중접속 방법이 피에조 소자 기반의 초음파 송수신 장치에서 가장 많이 사용된다.

US-CDMA를 위한 변조는 ID코드에 따라 신호를 송신하거나 송신하지 않는 OOK(On-OFF Keying) 방법[16], ID 코드에 따라 위상을 조정하는 PSK(Phase Shift Keying) 방법, ID 코드에 따라 송신 주파수를 조정하는 FSK(Frequency Shift Keying) 방법[17][18], ID 코드에 따라 처프(Chirp) 신호의 주파수 함수를 조정하는 처프 방식 등이 사용된다. 다양한 변조 방법은 각각의 장단점을 가지며 사용 환경에 적합한 방식을 사용한다. 초음파 장치가 이동체에 사용되면 상대 속도에 따라 도플러 효과가 발생한다. 상대 속도에 따라 수신 신호의 변화는 시간축과 주파수 축의 두 가지 변이가 생긴다. 시간 축으로는 수신 신호의 총 길이가 짧아지거나 길어지는 변화가 생기며 주파수 축으로는 주파수 천이가 발생한다. 다양한 변조 방법들은 도플러 효과에 영향을 받아, 각각의 특징에 맞게 복조 과정에서 오류가 발생한다.

이런 문제를 해결하기 위해 Teodoro는 처프 기반의 도플러 보상 알고리즘을 제안하였다[19]. 처프 신호는 압축된 펄스의 특징으로 도플러 효과의 속도를 추정하는데 유용하게 사용된다. 그러나 일반적으로 ToF 추정에 도플러 효과로 인해 문제가 발생하여 정밀도가 낮아지기 때문에 도플러 보상 알고리즘을 적용하여 정확한 ToF 추정을 하는 것을 제안한다. 하지만 처프로 코딩된 신호로 CDMA를 수행할 경우 한 비트당 전송시간이 길어 전체 패킷 전송에 상당한 시간이 소요된다. 또한 한 패킷 안에서 속도 변화가 발생할 경우 대처할 수 없는 문제가 있다. Karalikkadan는 범위-도플러 결합을 활용한 주파수 천이 추정방법을 제안하였다[20]. 하지만 복잡한 처프 신호 세트를 사용하고 초음파 노드 수에 맞는 최적화를 해야 하기 때문에 노드 수가 고정적인 환경에서만 사용할 수 있다.

본 논문에서는 처프 기반의 CDMA의 단점을 해결하기 위해 chirp-OOK 혼합 변조 방법을 제안한다. 도플러 효과의 속도 추정에 유용한 처프 신호를 사용하여 패킷 수신 시점의 상대 속도를 추정한다. ID 코드는 OOK에 포함되며 추정된 상대 속도 정보를 이용하여 대역통과필터를 조정하고 비교 코드의 업샘플링 간격을 조정한다. 최종적으로 도플러 효과가 보상되고 총 패킷 전송시간이 짧은 것을 목표로 한다.

본 논문의 구성은 다음과 같다. 2장은 제안하는 chirp-OOK 혼합 변조 신호에 대해 소개하고 처프와 OOK 복조기를 설명한다. 3장에서는 본 논문에서 제안하는 방법의 성능을 도플러 시뮬레이션을 통해 비교 검증한다.

마지막으로 4장에서는 결론에 대해 기술하고 본 연구가 갖는 한계점 및 향후 연구에 대하여 기술한다.

Ⅱ. Chirp-OOK 혼합 변조 방법

2.1 Chirp-OOK 혼합 변조 신호

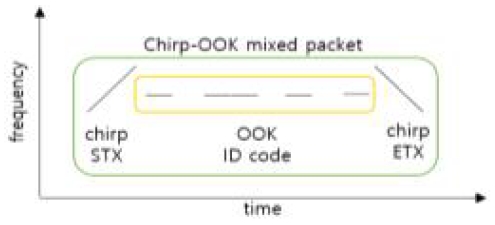
처프 신호의 주파수 천이 검출의 장점과 OOK 신호의 짧은 송신 시간의 장점을 합치기 위해 그림 1과 같은 변조 구성을 제안한다. 송신 패킷의 처음을 처프 상승 변조를 하고 마지막을 처프 하강 변조를 한다. 초음파의 중심주파수가 f_c일 때 처프 신호 $$ s_k^{chirp }\left(t\right)$$는 다음과 같다.

$\[ s_k^{chirp}\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi {\int }_0^t{f}_k\left(\tau \right)d\tau \right) \]$

(1)

Fig. 1.

Configuration of chirp-OOK mixed modulation

식 (1)의 f_x(t)는 처프의 순간 주파수이며 상승 변조일 경우 k = 1, 하강 변조일 경우 k = -1이다.

$\[ f_k\left(t\right)=k\frac{\Delta f}{\Delta t}\left(t-\frac{\Delta t}{2}\right)+f_c \]$

(2)

식 (2)의 Δf는 주파수 변화량, Δt는 전송시간이다. 이와 같이 구성하면 패킷의 처음과 마지막의 위치가 구분되어 신호 혼선에 강인함이 증가하고 주파수 천이량을 추정할 수 있다. OOK는 장치 노드의 코드가 변조되어 ID 인식 및 전파시간 추정에 사용된다.

$\[ s^{OOK}\left(t\right)=a\left(t\right)\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi f_{c}t\right) \]$

(3)

식 (3)의 a(t)는 노드 코드에 따라 코드 ‘1’의 경우 신호를 송신하기 위해 1 코드 ‘0’의 경우 송신하지 않기 위해 0의 값을 가진다.

$\[ a\left(t\right)=\left\{\begin{array}{cc}1\hfill & ,code = 1\hfill \\ 0\hfill & ,code = 0\hfill \end{array}\right. \]$

(4)

OOK는 chirp에 비하여 한 비트당 전송시간이 짧아 패킷의 총 전송시간이 줄어든다. 또한 처프 신호로 추정된 상대 속도 정보를 이용하여 도플러 효과를 보상한 OOK 디코딩 및 CDMA 복조 과정을 수행한다.

2.2 수신 신호의 복조 과정

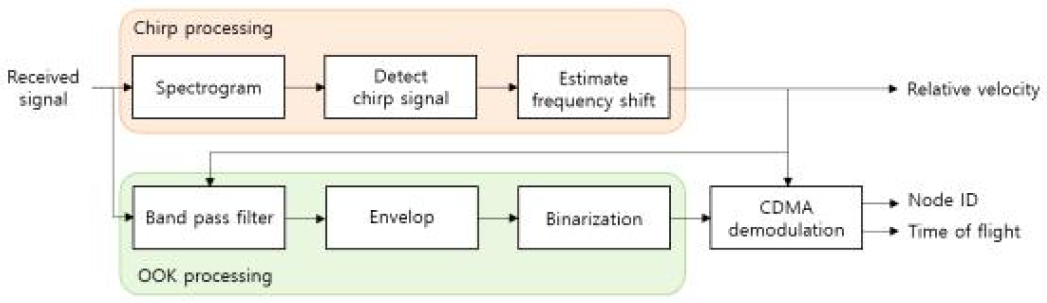
수신 신호의 그림 2와 같이 복조 과정은 처프 신호 처리 과정과 OOK 신호처리 과정으로 나누어 처리된다. 처프 처리 과정은 스펙트로그램 변환, 처프 신호 검출, 주파수 천이 추정 과정을 통해 도플러 효과가 발생하는 상대속도를 계산한다. OOK 처리 과정은 주파수 천이량을 고려한 대역 통과 필터를 통해 잡음 대 신호 비를 향상시키고 신호 코드 검출을 위해 포락선 및 이진화를 수행한다. 마지막으로 코드 시간 압축비를 고려한 CDMA 복조를 수행하여 수신 신호의 노드 ID와 신호 전송시간을 검출한다. 우선 수신 신호 s_rx를 STFT(Short Time Fourier Transform)기반의 스펙트로그램으로 변환하는 수식은 다음과 같다.

$\[ S_{rx}\left(n,f\right)={\left|\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}{s}_{rx}\left[m\right]w\left[m-n\right]e^{-j2\pi fm}\right|}^2 \]$

(5)

Fig. 2.

CDMA demodulation process of chirp-OOK mixed modulated signal

여기서 w[n]은 윈도우 함수이고 다음의 Kaiser 윈도우 함수를 사용하였다.

$\[ w\left[n\right]=\frac{I_0\left[1-{\left(\frac{2n}{N}-1\right)}^2\right]}{I_0\beta }, 0\le n\le N \]$

(6)

식 (6)의 I₀는 0차 변형 베셀 함수이고 N은 윈도우 길이 그리고 β는 Kaiser 윈도우의 특징 변수이다.

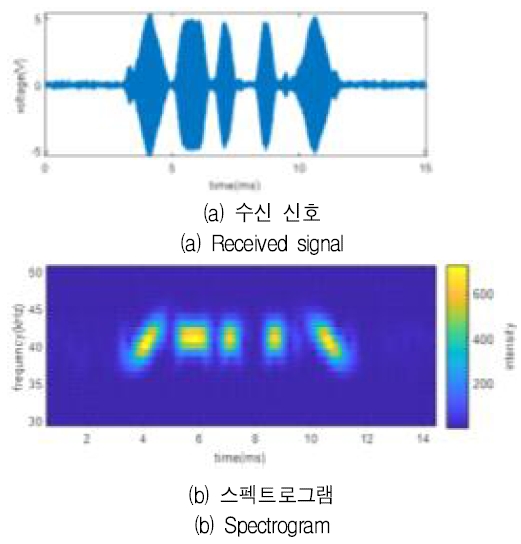
그림 3은 수신 신호 s_rx와 스펙트로그램 S_rx를 보여준다. 변환된 스펙트로그램에서 처프 신호를 검출하기 위해 처프 신호와 유사한 형상의 mask와 상호상관을 수행한다.

Fig. 3.

Received signal and spectrogram

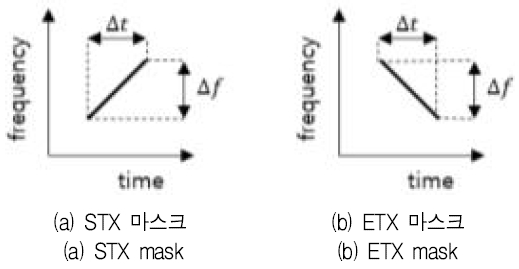
Mask는 그림 4와 같이 시간 축으로 Δt, 주파수 축으로 Δf크기를 가지고 양의 기울기를 가지는 STX mask와 음의 기울기를 가지는 ETX mask가 있다. 스펙트로그램 신호 S_rx와 chirp mask M_stx 및 M_etx와의 상호상관은 다음과 같이 계산된다.

$\[ {\rho }_{stx}\left[n\right]=\sum _{m=m_0}^{m_{\text{max}}}\sum _{f=f_0}^{f_{\text{max}}}{S}_{rx}\left(n+m,f\right)M_{stx}\left(m,f\right) \]$

(7)

$\[ {\rho }_{etx}\left[n\right]=\sum _{m=m_0}^{m_{\text{max}}}\sum _{f=f_0}^{f_{\text{max}}}{S}_{rx}\left(n+m,f\right)M_{etx}\left(m,f\right) \]$

(8)

Fig. 4.

Chirp signal mask

식 (7)과 식 (8)에서 변수값 m₀ =-Δt/2, m_max = Δn/2, f₀ = f_c - Δf/2, f_max = f_c + Δf/2이다. 처프 신호의 중심 위치는 상호상관이 최대가 되는 지점으로 다음과 같다.

$\[ n_{stx}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathrm{n}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\rho }_{stx}\left[n\right]\right) \]$

(9)

따라서 처프 stx 신호는 식 (10)으로 정의한다.

(10)

또한, etx 신호는 식 (11)로 정의한다.

(11)

여기서 신호의 주파수 최소값과 최대값의 중앙값을 천이된 주파수로 계산하면 식 (12), 식 (13)과 같다.

$\[ {\widehat{f}}_{stx}=\frac{\underset{f}{\text{min}}\left(S_{stx}\left(n,f\right)\right)+\underset{f}{\text{max}}\left(S_{stx}\left(n,f\right)\right)}{2} \]$

(12)

$\[ {\widehat{f}}_{etx }=\frac{\underset{f}{\text{min}}\left(S_{etx}\left(n,f\right)\right)+\underset{f}{\text{max}}\left(S_{etx}\left(n,f\right)\right)}{2} \]$

(13)

마지막으로 각 처프 신호에서 계산된 상대 속도는 다음과 같다.

$\[ v_{stx}=v_s\left(\frac{{\widehat{f}}_{stx}}{f_c}-1\right) \]$

(14)

$\[ v_{etx}=v_s\left(\frac{{\widehat{f}}_{etx}}{f_c}-1\right) \]$

(15)

여기서 v_s는 음파의 속도이다. OOK의 복조 과정은 잡음에 민감한 특징을 가진다. 따라서 신호 대 잡음비를 상승시키기 위해 대역 통과 필터를 수행한다. 필터의 대역은 앞서 계산한 주파수 천이를 고려하여 다음과 같이 계산된다.

$\[ f_L=\text{min}\left({\widehat{f}}_{stx},{\widehat{f}}_{etx}\right)-\Delta f/2 \]$

(16)

$\[ f_H=\text{max}\left({\widehat{f}}_{stx},{\widehat{f}}_{etx}\right)+\Delta f/2 \]$

(17)

본 논문에서는 48차 FIR 대역통과필터를 사용하였다. 대역통과된 신호 s_bpf[n]은 다음과 같다.

$\[ s_{bpf}\left[n\right]=\mathrm{B}\mathrm{P}\mathrm{F}\left(s_{rx}\left[n\right]\right) \]$

(18)

대역 통화된 신호는 변조된 사인파이기 때문에 힐베르트 변환의 복소 크기를 통해 포락선을 검출하면 다음과 같다.

$\[ a\left[n\right]=\left|H\left[s_{bp.f}\left[n\right]\right]\right| \]$

(19)

다음으로 이진화를 위해 문턱값을 계산한다. 문턱값은 잡음의 표준편차 σ_n을 검출한 뒤 99% 이상의 확률로 잡음과 신호를 구분하기 위해 3시그마를 적용하여 T_n = 3σ_n로 문턱값을 계산한다. 다음으로 계산된 문턱값보다 크면 1로 이진화를 한다.

$\[ c_{rx}\left[n\right]=\left\{\begin{array}{cc}1\hfill & ,a\left[n\right]>T_n\hfill \\ 0\hfill & , other\hfill \end{array}\right. \]$

(20)

CDMA 복조를 위해 변환된 업셈플링 ID 코드를 구한다.

$\[ c_{ID}\left[n\right]=C_{ID}{\left[m\right]}_{\uparrow L\left(m\right)} \]$

(21)

식 (21)의 L은 업 샘플링 요소로써 각 비트별 상대속도 v(n)을 고려하여 식 (22)와 같이 계산된다.

$\[ L\left(m\right)=\frac{v\left(n\right)+v_s}{v_s}\frac{\Delta t}{f_s} \]$

(22)

여기서 각 비트별 상대 속도 v(n)은 다음과 같이 계산된다.

$\[ v\left(n\right)=v_{stx}+n\frac{v_{etx}-v_{stx}}{L_{ID}} \]$

(23)

식 (23)의 L_ID는 ID 코드의 비트 수이다. 변환된 업셈플링 ID 코드c_ID와 이진화된 수신 코드c_rx의 상호상관을 계산하면 다음과 같다.

$\[ {\rho }_c\left[n\right]=\sum _{m=0}^{L_u{L}_{ID}}{c}_{rx}\left[n+m\right]c_{ID}\left[m\right] \]$

(24)

최종적으로 획득한 상호상관 값의 가장 빠른 인덱스가 수신 시점이므로 다음과 같이 TOF가 계산된다.

$\[ n_f=\text{min}\left\{x\left|{\rho }_c\left[x\right]=L_{ID}\right.\right\} \]$

(25)

$\[ t_f=n_f/f_s \]$

(26)

Ⅲ. 실 험

본 논문의 제안한 방법을 검증하기 위해 실제 환경에서 chirp-OOK 혼합 변조 신호를 송수신 하고 이 데이터를 기반으로 도플러 변환 시뮬레이션을 통해 복조기 검증을 진행하였다. 초음파 신호 송수신 환경은 그림 5와 같다.

Fig. 5.

Chirp-OOK mixed modulation signal transceiver environment

그림 5의 (a)를 보면 초음파 센서는 하기소닉 사의 HG-L40DC이고 중심 주파수 f_c가 40 kHz이고 대역폭이 4 kHz인 초음파 송수신기를 사용하였다. 또한 송수신기 주변으로 흡음재를 부착하여 다중경로 문제를 최소화하였다. 그림 5의 (b)를 보면 초음파 송수신 장치와 MCU 및 PC를 볼 수 있다. MCU에서 chirp-OOK 혼합 변조 신호를 생성해 송신하고 ADC를 통해 데이터를 수신한다. ADC 셈플링 주파수는 1 MHz이다. 수집된 데이터는 PC로 전송되어 복조 연산을 수행한다. 초음파 수신 데이터 세트는 송수신기의 거리 및 코드를 변경하여 총 100개로 구성된다. 도플러 변환 시뮬레이션은 matlab 2023을 통해 수행되었다. 본 논문에서 제안한 방법은 일반적인 OOK와 Teodoro의 도플러 보상 방법과 비교 검증한다.

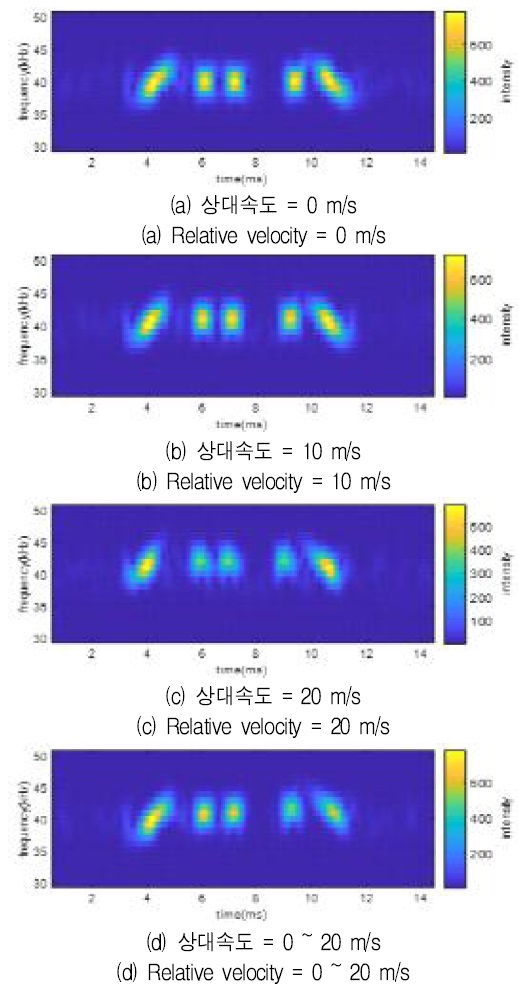
그림 6은 도플러 시뮬레이션된 수신신호이다. 도플러 시뮬레이션은 상대 속도를 정적 및 동적으로 변경 가능하며 스펙트로그램으로 확인 한 결과 상대 속도에 따라서 주파수 천이가 발생하였다.

Fig. 6.

Doppler simulation results

3.1 처프 속도 추정 성능 검증

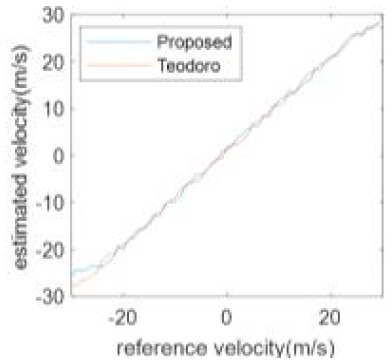
처프 신호의 도플러 속도 추정 성능 검증을 위해 고정 상대속도 노드와 가속하는 노드의 속도를 제안하는 방법과 Teodoro의 방법으로 비교하였다. 그림 7은 일정한 상대 속도일 때 노드 속도에 따른 추정 속도의 결과를 보여준다. 제안 방법의 속도는 v_stx와 v_etx의 평균값으로 표기하였다. 실험 결과 제안 방법의 경우 속도 추정의 RMSE(Root Mean Square Error)는 1.51이고 오차의 표준편차는 1.15이였다.

Fig. 7.

Speed ​​estimation results for fixed speed nodes

Teodoro 방법의 RMSE는 1.23이고 오차의 표준편차는 0.71이였다. 두 방법 비슷한 성능을 보여주었다. 노드 속도가 25 m/s이상일 경우 주파수 천이량이 커져 초음파 송수신기의 대역 제한으로 인해 신호 감쇠로 추정 속도 오차가 커지는 경향을 보였다.

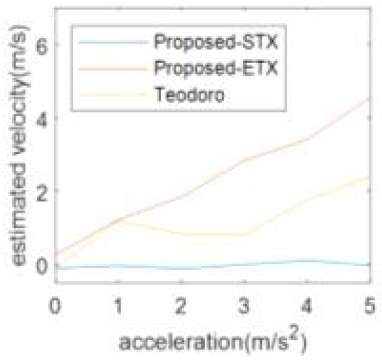
그림 8은 정지상태에서 가속하는 노드의 속도 추정 결과이다. 제안 방법의 경우 v_stx와 v_etx를 분리하여 표기하였다. 제안 방법의 RMSE는 0.31이고 표준편차는 0.34이다. Teodoro 방법의 경우 가속도가 2 m/s²부터 오차가 급격하게 커져 RMSE는 1.17 표준편차는 1.18을 보였다. Teodoro 방법의 경우 가속 상황을 고려하지 않아 가속도가 일정 이상 커지자 도플러 보상 알고리즘에 문제가 발생하였다. 처프 속도 추정 성능 검증 결과 가속도가 0 m/s²인 상황에서는 두 방법이 유사한 성능을 보였으나 가속도가 2 m/s²이상인 상황에서는 제안 방법의 속도 추정 성능이 더 좋은 것으로 나타났다.

Fig. 8.

Speed ​​estimation results of acceleration nodes

3.2 도플러 효과에 따른 ToF 정확도 비교

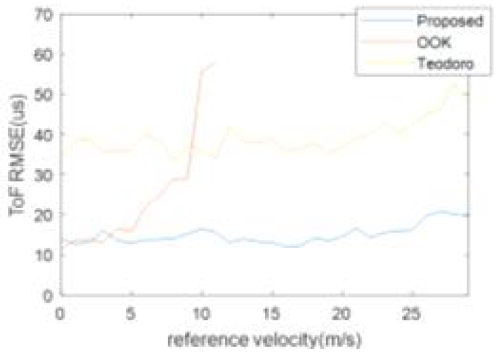
도플러 효과에 따른 알고리즘별 ToF 정확도를 비교한 결과는 그림 9에서 볼 수 있다. 노드 상대 속도 0 m/s부터 30 m/s까지 제안 방법, OOK, Teodoro 방법을 비교하였다. 제안 방법은 ToF 계산을 OOK 기반으로 수행하기 때문에 도플러 속도가 낮을 때 일반적인 OOK와 유하산 RMSE를 가진다. 하지만 일반적인 OOK는 도플러 속도가 증가함에 따라 시간축 늘어짐이 발생하여 ToF 오차가 커진다. 시간축 늘어짐이 ID 코드의 한 비트보다 커질 경우 ID 추정이 불가능하여 약 10 m/s 이상의 상대속도에서는 CDMA 복조 과정에서 ID가 검출되지 않는다. Teodoro 방법은 chirp 기반으로 ToF 계산을 수행하기 때문에 OOK 기반의 방법보다 ToF 오차가 약 3배 더 큰 결과를 보였다. 제안 방법은 도플러 속도에 상관없이 RMSE가 20이하를 가지며 이는 거리오차로 6 mm 이하로 환산된다.

Fig. 9.

ToF accuracy comparison according to relative speed

Ⅳ. 결 론

초음파 CDMA에서의 도플러 효과로 인한 ToF 정확도 저하, 코드 검출 실패, 패킷 전송 시간 증가등의 문제를 해결하기 위해 본 논문에서는 chirp-OOK 혼합 변조 방법을 제안했다. 처프 신호의 뛰어난 주파수 천이 추정 특징을 활용해 전송 패킷의 상대 속도를 계산한다. 추정한 상대 속도를 바탕으로 OOK 복조기를 조정하여 복조 오류를 방지한다.

본 논문에서 제안한 방법의 성능을 일반적인 OOK 방법, Teodoro의 처프 기반의 도플러 보상 방법과 비교분석 하였다. 처프의 도플러 속도 추정 성능은 장치가 감가속되지 않는 정속도 환경일 때, 속도 추정 RMSE는 본 논문에서 제안한 방법 1.51 m/s와 Teodoro의 방법 1.23 m/s의 성능을 보였으나 장치가 가속되는 환경일 경우 제안한 방법 0.31 m/s, Teodoro의 방법 1.17 m/s로 제안한 방법이 감가속 상황에서 강인한 성능을 보였다. 최종적인 ToF 성능평가에서 일반적인 OOK의 경우 ToF RMSE가 16.3 us 정도로 작으나 상대속도 10 m/s 이상 커짐에 따라 ID 코드 검출 실패로 측정이 불가능하고, Teodoro의 방법은 처프 CDMA를 수행하기 때문에 ToF RMSE가 42.8 us로 부정확한 결과를 보였다. 하지만 본 논문에서 제안한 방법은 상대 속도에 상관없이 ToF RMSE 17.1 us로 가장 안정적이고 정확한 성능을 보였다.

실험결과를 미루어 보아, 짧은 패킷 전송시간을 요구하는 실내 단거리 이동체의 초음파 감지 장치 등의 용도에 본 논문에서 제안한 방법을 사용한다면 기존의 방법보다 안정적이고 정확한 ToF 추정 성능을 보일 것으로 기대한다.

Acknowledgments

본 논문은 부산대학교 기본연구지원사업(2년)에서 지원하여 연구하였음

References

• M. Kelemen, I. Virgala, T Kelemenova, L. Mikova, P. Frankovsky, T. Liptak, and M. Lorinc, "Distance measurement via using of ultrasonic sensor", Journal of Automation and Control, Vol. 3, No. 3, pp. 71-74, 2015. [https://doi.org/110.12691/automation-3-3-6]
• S. Laureti, M. Mercuri, D. A Hutchins, and F. Crupi, M. Ricci, "Modified FMCW Scheme for Improved Ultrasonic Positioning and Ranging of Unmanned Ground Vehicles at Distances < 50 mm", Sensors, Vol. 22, No. 24, Dec. 2022. [https://doi.org/10.3390/s22249899]
• J. Jodhani, A. Handa., A. Gautam, and R Rana, "Ultrasonic non-destructive evaluation of composites: A review", Materials Today, Vol. 78, No. 3, pp. 627-632, 2023. [https://doi.org/10.1016/j.matpr.2022.12.055]
• M. Hasan, "Applications of Ultrasonic Testing (UT) for Irregularities Detection in Human Body and Materials: A Literature Review", International Journal of Occupational Hygiene, Vol. 13, No. 1, pp. 91-104, May 2021.
• W. Xue, M. Yang, D. Hong, D. Wu, Y. Wang, and X. Qing, "The design and verification of an active SAMSR ultrasonic guided wave monitoring system with ultra-low crosstalk", Sensors, Vol. 20, No. 3, pp. 898, Feb. 2020. [https://doi.org/10.3390/s20030898]
• S. Shin, M. H. Kim, and S. B. Choi, "Ultrasonic Distance Measurement Method With Crosstalk Rejection at High Measurement Rate", in IEEE Transactions on Instrumentation and Measurement, Vol. 68, No. 4, pp. 972-979, Apr. 2019. [https://doi.org/10.1109/TIM.2018.2863999]
• S. H. Park, S. H. Park, and K. R. Baek, "Phase Based on Off Keying Demodulator for Reducing Ultrasonic Cross-talk", The Journal of Korean Institute of Information Technology, Vol. 20, No. 7, pp. 95-101, Jun. 2022. [https://doi.org/10.14801/jkiit.2022.20.7.95]
• C. Medina, J. C. Segura, and Á. Torre, "A Synchronous TDMA Ultrasonic TOF Measurement System for Low-Power Wireless Sensor Networks", in IEEE Transactions on Instrumentation and Measurement, Vol. 62, No. 3, pp. 599-611, Mar. 2013. [https://doi.org/10.1109/TIM.2012.2218056]
• P. Cheng, F. Zhang, J. Chen, Y. Sun, and X. Shen, "A Distributed TDMA Scheduling Algorithm for Target Tracking in Ultrasonic Sensor Networks", in IEEE Transactions on Industrial Electronics, Vol. 60, No. 9, pp. 3836-3845, Sep. 2013. [https://doi.org/10.1109/TIE.2012.2208439]
• S. Haigh, J. Kulon, A. Partlow, P. Rogers, and C. Gibson, "Improved Obstacle Mitigation and Localization Accuracy in Narrowband Ultrasonic Localization Systems Using RoBCUL Algorithm", in IEEE Transactions on Instrumentation and Measurement, Vol. 69, No. 5, pp. 2315-2324, May. 2020. [https://doi.org/10.1109/TIM.2019.2963553]
• C. Medina., J. C. Segura, and A. Torre, "Ultrasound indoor positioning system based on a low-power wireless sensor network providing sub-centimeter accuracy", Sensors, Vol. 13, No. 3, pp. 3501-3526, Mar. 2013. [https://doi.org/10.3390/s130303501]
• M. Stojanovic and L. Freitag, "Multichannel Detection for Wideband Underwater Acoustic CDMA Communications", in IEEE Journal of Oceanic Engineering, Vol. 31, No. 3, pp. 685-695, Jul. 2006. [https://doi.org/10.1109/JOE.2006.880389]
• M. C. Pérez-Rubio, et al., "Simulation tool and online demonstrator for CDMA-based ultrasonic indoor localization systems", Sensors, Vol. 22, No. 3, pp. 1038, Dec. 2021. [https://doi.org/10.3390/s22031038]
• A. Suzuki, K. Kumakura, Y. Choi, and T. Iyota, "Accuracy of distance measurements using signal tracking of spread-spectrum ultrasonic waves with CDMA", 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, pp. 575-581, Oct. 2014. [https://doi.org/10.1109/IPIN.2014.7275530]
• M. Oberdorfer, D. Esslinger, G. Benz, O. Sawodny, and C. Tarin, "Robustness enhancements of time-of-flight measurements in a CDMA ultrasonic channel of an opto-acoustic indoor positioning system using MEMS microphones", 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, pp. 1-6, Sep. 2020. [https://doi.org/10.1109/IUS46767.2020.9251546]
• J. Oetting, "A Comparison of Modulation Techniques for Digital Radio", in IEEE Transactions on Communications, Vol. 27, No. 12, pp. 1752-1762, Dec. 1979. [https://doi.org/10.1109/TCOM.1979.1094370]
• B. Watson, "FSK: signals and demodulation", Watkins–Johnson Company Tech–notes, Vol. 7, No. 5, Sep. 1980.
• K. Nakahira, S. Okuma, T. Kodama, and T. Furuhashi, "The use of binary coded frequency shift keyed signals for multiple user sonar ranging", IEEE International Conference on Networking, Sensing and Control, Taipei, Taiwan, Vol. 2, pp. 1271-1275. Mar. 2004. [https://doi.org/10.1109/ICNSC.2004.1297130]
• T. Aguilera, F. J. Álvarez, J. A. Paredes, and J. A. Moreno, "Doppler compensation algorithm for chirp-based acoustic local positioning systems", Digital Signal Processing, Elsevier, Vol. 100, pp. 102704, May 2020. [https://doi.org/10.1016/j.dsp.2020.102704]
• J. Aparicio, T. Aguilera, and F. J. Álvarez, "Robust Airborne Ultrasonic Positioning of Moving Targets in Weak Signal Coverage Areas", IEEE Sensors Journal, Vol. 20, No. 21, pp. 13119-13130, Nov. 2020. [https://doi.org/10.1109/JSEN.2020.3003523]