시공간 블록 코드의 부호 반전 데이터 시퀀스 기법
초록
본 논문은 시공간 블록 코드 송수신 기법에서의 부호 반전 기법이 적용되는 데이터 시퀀스에 관한 기술을 제안한다. 제안하는 기술은 최근에 발생하고 있는 공개된 전파의 하이재킹 문제를 해결하기 위한 연구이며, 단순하게 송신하는 데이터를 교환하여 전송하는 것을 부호 반전 기법을 적용하여 송수신 환경 파라미터들을 바꿈으로써 제 3의 수신자들이 공개된 전파를 수신하더라도 직교 주파수 분할 다중화 시스템의 각 블록 기반들의 데이터 복호를 어렵게 한다. 시공간 블록 코드 기법에서 종래의 방법보다 다양한 16가지 변종으로 적용가능한 이 기법은 전송하는 데이터 시퀀스를 모르는 인접 수신기들이 전파를 수신하더라고 데이터 복호가 얼마나 어렵게 진행되는가 하는 것을 모의실험하여 제안하는 알고리즘의 성능을 제시하고자 한다.
Abstract
This paper proposes a data sequence technique to be used in sign reversal technology for Space-Time Block Code. The proposed technology is a study to solve the problem of hijacking of public radio waves that has been occurring recently, by applying a sign reversal technique to change the parameters of the transmission and reception environment from simply exchanging and transmitting data, it makes third party receivers difficult to decode data applicable to each block of the orthogonal frequency division multiplexing system even if they may capture open radio waves. This technique of 16 different variants compared with the conventional method, applicable to the space-time block code technique, aims to present the performance of the proposed algorithm by simulating how difficult it is to decode data even though adjacent receivers who do not know the transmitted data sequence receive radio waves.
Keywords:
data protection, data sequence, random code, sign reversal, space-time block codeⅠ. 서 론
무선 환경에서 특히 무선 랜과 같은 실내 무선 환경에서 다중 송수신기 안테나를 사용하는 경우에는 다중 반송파 방식인 직교 주파수 분할 다중화(OFDM, Orthogonal Frequency Division Multiplexing) 방식이 다중 경로 페이딩을 겪고 있는 무선 전파 환경에서 효과적으로 대응하는 것으로 알려져 사용되고 있다[1]. 이와 같은 무선 환경은 전파들이 무작위하게 산란하여 퍼지는 환경이며 이와 같은 전파 환경에서 소비전력 관점에서 최적의 효율을 보여주는 방식이 최대 율 수신 결합으로 알려져 있다. 또한 이와 같은 수신 결합 방식을 송신기 관점에서 사용하고자 하는 방식이 시공간 블록 코드 방식이며, 이 알고리즘은 다중 송수신 안테나의 활용이 가능하게 한 통신 알고리즘으로 알려져 있다[2][3]. 한편 이와 같은 알고리즘을 다중 반송파 통신 방식 뿐만 아니고 단일 반송파 시스템에서 적용하고자 하는 알고리즘, 즉 다중 반송파 방식의 송신기에서 사용되는 푸리에 역 변환기를 송신기에서 사용하지 않음으로써 송신기의 신호는 시간 영역 신호를 사용하고, 수신기에서는 송신기에서 사용하던 푸리에 역 변환기를 채널 보상기 및 채널 추정 및 결합 이후에 사용함으로써 데이터 송수신이 가능하게 하였다[4].
이와 같은 다중 송수신 안테나 시스템에서는 각 안테나 별로 전송되는 신호는 수신기에서의 다이버시티 결합이 가능하게 되는 결합 구조를 고려하여 전송하여야 하며 이와 같은 구조로는 시공간 블록 코드를 들 수 있다. 한편 이와 같은 무선 전파들은 제 3자에 의해서 전파 수신이 가능하며 이와 같은 전파의 수신시 해킹 알고리즘으로 송수신 데이터를 탈취하는 현상이 발생하고 있다[5]. 이와 같은 상황에서 보내는 송신 데이터의 보내는 순서를 간단하게 바꾸는[6] 만으로도 수신기에서 결합되는 알고리즘이 변형됨에 따라 전파는 수신되더라도 데이터 복호가 어렵게 되는 방식이 또한 연구되어 왔다. 이와 같은 알고리즘은 송신기에서의 복잡도가 상당하여 실현 복잡도가 증가하였으므로 그 복잡도를 감소시키는 연구로서 부호 반전 알고리즘이 제안되었다[7]. 이렇게 제안된 부호 반전 알고리즘은 간단하게 송신 블록들의 부호 반전을 실시함으로써 수신기에서 부호 반전이 일어난 데이터 블록들을 모르면 수신기에서 데이터 결합이 어려워지는 상황을 초래하게 된다. 이렇게 제안된 부호 반전 알고리즘에서 부호 반전을 발생시키는 방식을 다양하게 제안하고 그 알고리즘을 공간 주파수 블록 코드 방식에 적용하여 데이터 심볼 각각마다 적용함으로써 수신기에서의 데이터 복호를 어렵게 하는 알고리즘이 제안되었다[8]. 한편 이와 같은 부호 반전을 직교 주파수 분할 다중화 시스템의 시공간 블록 코드에서 부호 반전을 4가지 종류로 다양화하여 실행하고자 하는 알고리즘[9]이 제안되었다.
한편 그동안 제안된 논문들은 부호 반전 송신 신호 구성 종류가 많지 않음으로, 본 논문에서는 송신 안테나 2개, 수신안테나 1개로 구성된 시공간 블록 코드에서 구성가능한 모든 경우의 부호 반전 알고리즘을 제안하고, 그 각각의 경우의 수신기에서의 채널 결합 방법을 제안하여 전파가 공개되어 있는 상황에서도 제 3자에 의해 송수신 데이터 탈취를 어렵게 만드는 데이터 시퀀스 알고리즘을 제안하고자 한다.
본 논문의 구성은 다음과 같다. 2장에서는 제안하는 부호 반전 데이터 시퀀스의 알고리즘을 구성하는 방법에 대해서 설명하고 부호 반전 데이터 시퀀스 알고리즘을 사용하는 않는 시스템과 비교하고자 한다. 3장에서는 제안하는 알고리즘의 데이터 보호 방법이 효과적임을 설명하는 모의실험 및 성능비교에 관하여 기술한다. 마지막으로 4장에서는 결론을 맺고 앞으로의 연구 방향에 대하여 기술한다.
Ⅱ. 부호 반전 데이터 시퀀스 알고리즘
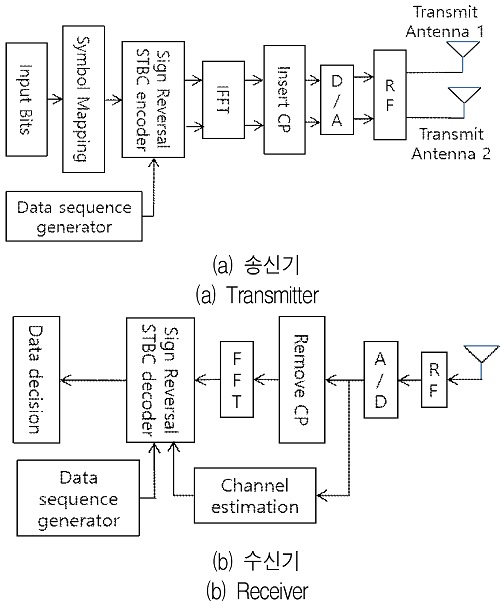
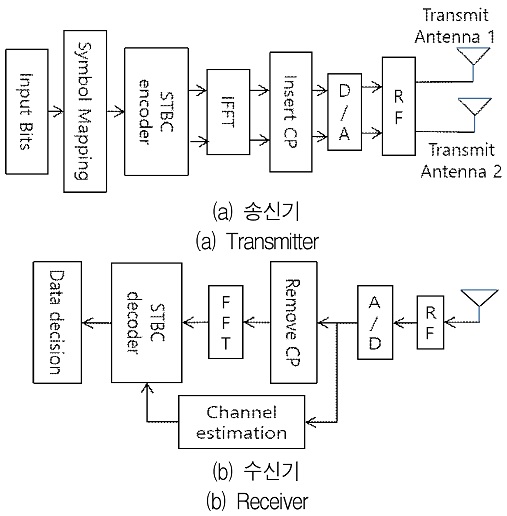
그림 1은 제안하는 부호 반전 데이터 시퀀스 알고리즘의 직교 주파수 분할 다중화 시스템의 시공간 블록 코드 방식에 적용한 블록도이며, 그림 2는 종래의 직교 주파수 분할 다중화 시스템의 시공간 블록 코드 방식의 블록도이다. 그림 1(a) 송신기의 Input Bits 블록은 사용자 데이터를 말하며, 데이터 시퀀스 발생기에 의하여 부호 반전 영역을 정하고 부호 반전 시공간 블록 코드 인코더를 거쳐 IFFT 블록에서 시간 영역으로 변환하고, RF 신호로 변환 후 두 개의 송신 안테나로 전송된다.
그림 1(b) 수신기에서는 RF 블록에서 기저대역으로 변환한 후 FFT 블록을 거쳐 주파수 영역 신호로 변환되며 채널 추정 및 송신기의 데이터 시퀀스에 맞춘 부호 반전 시공간 블록 코드 디코더를 거쳐 송신 신호를 추정하게 된다. 제안하는 알고리즘과 종래의 방법과의 차이점은 데이터 시퀀스 발생기 블록이며 이 블록은 송신기와 수신기에 각각 위치하며, 발생된 데이터 시퀀스에 따라 송신기에서는 부호 반전이 일어나며, 수신기에서는 송신기에서 부호 반전된 조합에 대응하여 데이터 수신 결합 방법이 변경되어야 한다. 송신기에서는 단순하게 부호만 변형해서 송신하지만, 수신기에서는 부호 반전에 따다 시공간 블록 코드의 결합 방법이 바뀌게 되고 그에 따라 시간 영역 신호, 수신 채널, 데이터 신호의 부호 등이 바뀌게 된다. 먼저 보내고자 하는 시공간 블록 코드의 송신 데이터 블록을 다음과 같이 구성하고 이 방법을 A0 라고 부르기로 한다.
| (1) |
여기서 (∙)*은 공액 복소수를 의미한다. 이때 부호 반전을 발생시키는 방법은 총 4개의 원소이므로 여러 가지를 구성할 수 있으나 수신기에서의 시공간 블록 코드 결합 방법이 가능한 구조로 구성하여야 한다. 이에 따라 구성 가능한 부호 반전 조합은 다음 표 1과 같다.
여기서 송신 데이터 행렬의 위치를 다음과 같이 가정한다. 또한 부호 반전이라 함은 + 부호는 –부호로, - 부호는 + 부호로 바꾸는 것을 말한다.
| (2) |
만일 보내고자 하는 시공간 블록 코드의 송신 데이터 블록을 가로와 세로를 바꾸어서 다음과 같이 구성하고 이 방법을 B0 라고 부르기로 한다.
| (3) |
이에 따라 구성 가능한 부호 반전 조합은 다음 표 2와 같다.
이와 같은 부호 반전 방법으로 송신기에서 구성가능한 부호 반전 방법은 모두 16종류의 구성을 가지게 된다. 그림 1의 제안하는 알고리즘의 송신기에서 두 개의 길이 N 의 사용자 데이터 블록을 송신 안테나 1과 2를 통하여 전송한다고 하자. 그러면 k-번째 직교 주파수 분할 다중화 심볼 주기동안에 전송되는 다음과 같이 표현 가능하다. 방법 A0 로 구성한 시공간 블록 코드로 송신한다고 가정하면,
| (4) |
그러면 (k+1)-번째 직교 주파수 분할 다중화 심볼 주기 동안에는 과 가 각각 송신 안테나 1과 2를 통하여 전송하게 된다. 여기에서 ( )*은 공액 복소수를 의미한다.
| (5) |
그림 1의 푸리에 역변환기에서는 위의 S1, S2, , 을 각각 시간 영역 데이터 블록 s1, s2, , 로 변환하여 길이 L 인 사이클릭 프레픽스(CP, Cyclic Prefix)를 추가한다. 이때 두 개의 연속된 직교 주파수 분할 다중화 심볼들의 채널들이 고정되어 있다고 가정한다. 이때 수신 안테나를 통하여 수신된 시간 영역 신호의 식을 기술하면 다음과 같다.
| (6) |
여기서, 은(N+L) × (N+L) 의 순환 행렬으로서 첫 번째 열이 채널 임펄스 응답에 영들이 추가된 것을 말하며, 그것은 m 번째 OFDM 심볼 주기에 n 번째 송신기로부터 수신기까지의 채널을 말하며, nk와 nk+1은 k-번째와 (k+1)-번째 OFDM 심볼 주기의 백색잡음을 의미하며, ⊗은 컨벌루션을 의미한다. 이 신호는 아이겐-분해 (Eigen-decomposition)[10]에 의하여 과 같이 정의되며, 여기에서 Q와 (∙)H은 각각 정규 직교 이산 푸리에 변환 행렬[11]과 복소수 공액 전치를 의미한다. 수신기에서 사이클릭 프레픽스를 제거한 후 길이 N 의 yk와 yk+1은 푸리에 변환기를 통하여 다음과 같은 주파수 영역 신호 Yk와 yk+1로 변환된다.
| (7) |
이때 수신기에서의 최대 율 결합 방법에 따른 결합 방법은 다음과 같으며, 이에 따라 송신 신호 S1과 S2의 각 원소들은 다음과 같다.
| (8) |
여기에서 n=0,1, ⋯, N-1, 그리고 그리고 를 가정하였다.
만일 송신기에서 부호 반전 A1 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (9) |
만일 송신기에서 부호 반전 A2 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (10) |
이 결과는 방법 A0에서 채널 과 를 바꾸고 송신 신호 S1과 S2를 교환한 것에 해당한다. 이것은 부호 반전으로 인하여 채널이 스위칭되고 소스 신호가 바뀌어서 전송된 결과를 보여준다.
만일 송신기에서 부호 반전 A3 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (11) |
만일 송신기에서 부호 반전 A4 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (12) |
만일 송신기에서 부호 반전 A5 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (13) |
만일 송신기에서 부호 반전 A6 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (14) |
만일 송신기에서 부호 반전 A7 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (15) |
만일 보내고자 하는 시공간 블록 코드의 송신 데이터 블록을 가로와 세로를 바꾸어서 방법 B0를 사용하여 데이터를 송신하면, 시간 영역 신호는 다음과 같다.
| (16) |
수신기에서 사이클릭 프레픽스를 제거한 후 길이 N 의 yk와 yk+1은 푸리에 변환기를 통하여 다음과 같은 주파수 영역 신호 Yk와 Yk+1로 변환된다.
| (17) |
이때 수신기에서의 최대 율 결합 방법에 따른 결합 방법은 다음과 같으며, 이에 따라 송신 신호 S1과 S2의 각 원소들은 다음과 같다.
| (18) |
만일 송신기에서 부호 반전 B1 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (19) |
만일 송신기에서 부호 반전 B2 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (20) |
만일 송신기에서 부호 반전 B3 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (21) |
만일 송신기에서 부호 반전 B4 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (22) |
이 결과는 방법 B0에서 부호 반전으로 인하여 시간축 상에서의 두 수신 신호 Yk과 Yk+1이 바뀌었고 송신 신호 S1과 S2를 교환된 것을 보여준다.
만일 송신기에서 부호 반전 B5 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (23) |
만일 송신기에서 부호 반전 B6 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (24) |
만일 송신기에서 부호 반전 B7 방법을 사용한다면, 수신기에서의 송신신호 추정값은 다음과 같은 수신 결합 방법을 사용하여 구할 수 있다.
| (25) |
시공간 블록 코드에서 송신 신호를 OFDM 심볼 시간대별로 전송하는가 아니면 송신 안테나별로 전송하느냐에 따라 A 그룹 또는 B 그룹으로 나누며, A0 와 B0 는 기본적인 시공간 블록 코드를 배열한 것이며 A1에서 A7 은 A0를 부호 반전으로 송신하는 것을 말하며, B1에서 B7은 B0를 부호 반전으로 송신하는 것을 의미한다. 이와 같이 부호 반전하는 경우 수신기에서의 결합 방법을 정리하면 표 3과 같다. 표 3에서는 각 방식들에서 부호 반전하여 송신한 결과 발생하는 수신기에서의 채널 스위칭 효과, 소스 데이터 변형 결과, 그리고 수신 데이터 심볼의 변형 결과를 정리하였다.
Ⅲ. 모의 실험 및 성능 평가
모의 실험은 제안하는 부호 반전 데이터 시퀀스 기법이 데이터 시퀀스를 모르는 인근의 수신기들의 수신 성능에 미치는 영향을 비트오류율로 측정하여 평가하고자 한다.
3.1 모의실험환경
모의실험 환경은 직교 주파수 분할 다중화 시스템에서 시행하였으며 실험 변수들은 다음과 같다. 시스템 전체 주파수 대역은 20MHz, 직교 주파수 분할 다중화 시스템 하나의 데이터 블록은 싸이클릭 프레픽스(16개)를 포함하여 총 80개의 데이터 심볼로 구성된다. 이 총 80개의 데이터 심볼 주기는 4.0㎲, 싸이클릭 프레픽스를 제외한 유효 심볼 주기는 3.2㎲ 그리고 보호 구간은 0.8㎲이다. 송신기에서는 데이터 페이로드 64개, 보호구간 16개인 데이터 심볼 80개를 기본으로 하여 시간 축으로는 두 개의 직교 주파수 분할 다중화 심볼과 안테나 축으로는 두 개의 송신 안테나에 송신되는 총 4개의 직교 주파수 분할 다중화 심볼을 하나의 시공간 블록 코드 그룹으로 묶어서 전송한다. 모의실험 환경에서 사용한 채널은 HiperLAN/2 채널 A를 사용하였고, 수신기에서는 채널 상태 정보를 알고 있는 상태를 가정하였으며, 채널 A를 구성하는 각각의 채널은 독립적으로 레일리 페이딩을 겪고 있으며 또한 각각 50 Hz의 도플러 주파수인 멀티 채널 모델을 사용하였다.
소스 데이터 심볼들을 전송하는 데이터 시퀀스 종류는 위에서 기술한 16종류의 부호 반전 시공간 블록 코드를 사용하였으며, 각 직교 주파수 분할 다중화 심볼마다 16종류(A0~A7, B0~B7)중 하나로 송신하였고, 부호 반전 종류를 의미하는 16종류는 각 직교 주파수 분할 다중화 심볼마다 4비트로 표현가능하여 송신기와 수신기 사이에 부가적인 데이터로 데이터 송수신 전에 미리 공유함으로써 데이터 송수신이 가능하게 한다. 따라서 데이터를 송수신하고자 하는 전체 데이터들이 결정되면 부호 반전을 발생시킬 수 있는 최대 속도로는 각 시공간 블록 코드 블록별로 4비트의 부가적인 부호 반전 코드를 전송하는 것이 오버헤드가 된다. 변조 수준은 무선 랜의 변조 방식인 2, 4, 6비트 즉 QPSK, 16 QAM, 64 QAM을 가정하여 실험하였다.
3.2 실험결과
그림 3은 각 실험 결과를 보이는데, (a) QPSK 결과는 변조 수준을 2비트로 실행한 결과이며, (b) 16 QAM과 (c) 64 QAM 결과는 각각 변조 수준을 4비트, 6비트로 실행한 결과이다. 그림 3에서의 그래프 중 “1/16 error”은 16개의 OFDM 심볼중에서 15개의 심볼의 데이터 시퀀스를 아는 경우(93.75%)의 성능 곡선이며, “1/64 error”, “1/256 error”, “1/1024 error”은 각각 64개, 256개, 1024개의 OFDM 심볼중에서 한 개의 심볼의 데이터 시퀀스를 모르는 경우의 성능 곡선을 말하는데 퍼센트로 표현하면 각각 98.4375%, 99.6094%, 99.9023%의 데이터 시퀀스를 아는 경우를 의미한다. 제안하는 부호 반전 데이터 시퀀스 기법은 그림에서 “No error” 로 표현된 곡선이며 성능 곡선이 마루 현상을 보이지 않는 정상적인 수신 성능을 보이고 있으며, 부호 반전 데이터 시퀀스를 대부분 알고 있는 1/1024(99.9023%)의 경우의 성능도 비트 오류 성능이 마루 현상을 보이는 것을 알 수 있다. 이 마루 현상의 경우에는 송신 전력을 아무리 증가시 켜도 비트 오류 확률이 개선되지 않는다는 것을 의미한다. 이와 같은 수신 성능은 변조 수준과는 무관하게 QPSK, 16 QAM, 64 QAM의 경우 모두 비슷한 결과를 보인다.
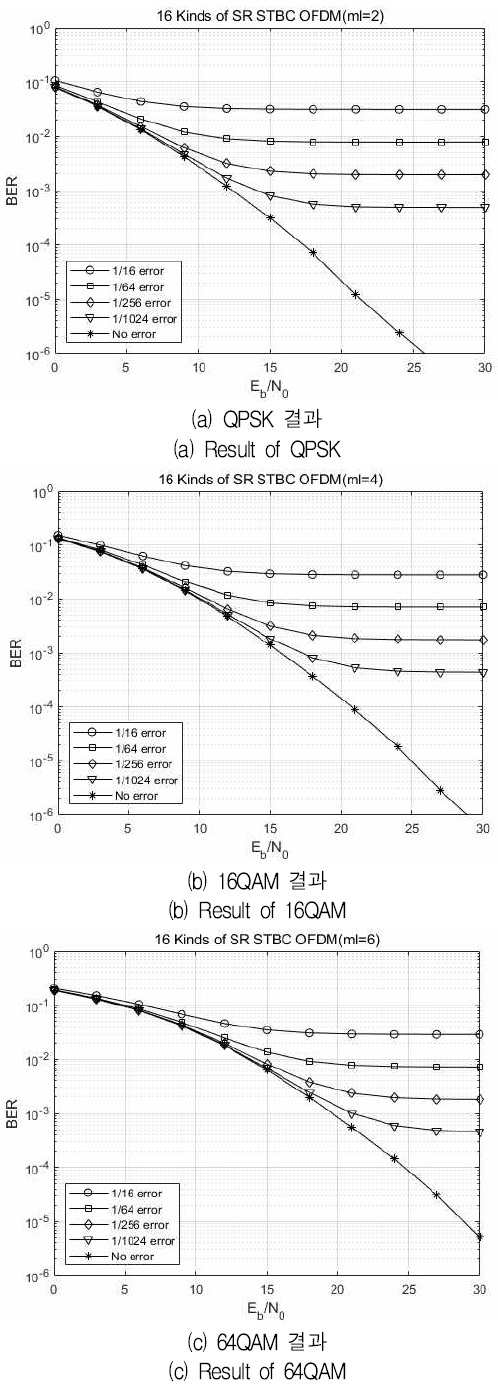
Performance comparison of the proposed sign reversal data sequence technique in space-time bock code
총 16종류의 부호 반전 시퀀스를 직교 주파수 분할 다중화 심볼 별로 랜덤으로 다르게 선택하여 그 시퀀스를 미리 보내어 송신하는 방법을 택한다면 그 데이터 시퀀스를 우연히 1023/1024(99.902%)를 아는 경우라 할지라도 비트 오류는 마루 현상을 보이며, 64 QAM의 모의실험결과 중 16개의 OFDM 심볼중에서 15개의 심볼의 데이터 시퀀스를 아는 경우(93.75%)라 할지라도 2.5-2정도의 비트오류율 특성을 보이므로 송신 데이터 시퀀스를 전혀 모르는 외부 수신기의 경우에는 데이터의 검출이 매우 어렵다는 것을 실험 데이터를 통하여 증명하였다.
Ⅳ. 결 론
본 논문에서는 직교 주파수 분할 다중화 시스템의 시공간 블록 코드의 송수신 데이터를 보호하는 방법을 제안하였다. 제안하는 알고리즘은 송신단에서는 시간 축 방향으로 그리고 송신 안테나 축 방향으로 구성된 시공간 블록 코드의 부호를 16 종류로 다양하게 반전시키는 방법을 제안하였으며 그렇게 반전된 데이터를 수신한 수신기에서는 전송된 데이터의 부호 반전 데이터 시퀀스를 알아야 정상적으로 수신이 가능함을 보였다. 제안하는 알고리즘을 직교 주파수 분할 다중화 시스템과 같은 다중 반송파 시스템에 적용가능하여 송수신기의 복잡도가 크게 증가하지 않는 데이터 보호방법을 제시하였다.
Acknowledgments
이 논문은 2023학년도 한밭대학교 교내학술연구비의 지원을 받았음
References
- IEEE SA 802.11 WG, IEEE P802.1n, Part 11, Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications, 2009.
-
S. M. Alamouti, "A simple transmit diversity technique for wireless communications", IEEE Journal on Selected Areas in Communications, Vol. 16, No. 8, pp. 1451-1458, Oct. 1988.
[https://doi.org/10.1109/49.730453]

-
W. G. Jeon and H. K. Jung, "Hybrid SC/MRRC Technique for OFDM Systems", IEICE Transactions on Communications, Vol. E89-B, No. 3, pp. 1003-1006, Mar. 2006.
[https://doi.org/10.1093/ietcom/e89-b.3.1003]

-
N. Al-Dhahir, "Single-Carrier Frequency Domain Equalization for Space-Time Block-Coded Transmisions Over Frequency Selective Fading Chanels", IEEE Communications Letters, Vol. 5, No. 7, pp. 304-306, Jul. 2001.
[https://doi.org/10.1109/4234.935750]

- Bombal David, "Brute force WiFi WPA2", https://www.youtube.com/watch?v=J8A8rKFZW-M, , [accessed: Nov. 10, 2023.]
-
H. K. Jung, "A simple Encryption Technology for Space-Time Block Coding", Journal of the Korea Industrial Information Systems, Vol. 23, No. 5, pp. 1-8, Oct. 2018.
[https://doi.org/10.9723/jksiis.2018.23.5.001]

-
H. K. Jung, "Sign Reversal Channel Switching method in Space-Time Block Code for OFDM Systems", IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, Vol E103-A, No. 2, pp. 567-570. Feb. 2020.
[https://doi.org/10.1587/transfun.2019EAL2090]

-
H. K. Jung, "Sign Reversal Channel Switching Method for Space-Frequency Block Code in Orthogonal Frequency Division Multiplexing System", Journal of the Korea Industrial Information Systems Research, Vol. 25, No. 5, pp. 13-21, Oct. 2020.
[https://doi.org/10.9723/jksiis.2020.25.5.013]

-
H. K. Jung, "Random Coded Data Protection Technique in Space-Time Block Code", The Transactions of the Korea Institute of Electrical Engineers, Vol. 70P, No. 4, pp. 270-276. Dec. 2021.
[https://doi.org/10.5370/KIEEP.2021.70.4.270]

- G. Strang, "Linear algebra and its applications", Cengage Learning, 4th ed., pp. 273-274, Jan. 2006.
- A. Oppenheim and R. Schafer, "Discrete-Time Signal Processing", 3rd ed., Prentice-Hall Englewood Cliffs, pp. 575-577, 1989.

1985년 2월 : 연세대학교 전기공학과(공학사)
1987년 2월 : 연세대학교 전기공학과(공학석사)
2004년 2월 : 중앙대학교 전자공학과(공학박사)
2004년 9월 ~ 현재 : 국립한밭대학교 모바일융합공학과 교수
관심분야 : OFDM 통신 시스템, 무선 랜, 딥러닝 신호처리