바이어스 추정을 위한 표본의 수가 자이로 센서의 드리프트 오차에 미치는 영향
초록
자이로 센서는 회전각을 추정하는 원리상 드리프트 오차라고 하는 문제를 갖는다. 본 논문에서는 바이어스 추정을 위한 표본의 수가 자이로 센서의 드리프트 오차에 미치는 영향을 검토한다. 이를 위해 5가지 조건으로 표본의 수를 바꾸어 가면서 드리프트 오차를 측정하고 비교 평가하는 실험을 반복 수행한다. 실험 결과, 바이어스를 추정하기 위한 표본의 수가 더 많을수록 드리프트 오차의 증가율이 감소한다는 사실을 알 수 있었다. 특히, 표본의 수를 10에서 1,000으로 증가시켰을 때, 드리프트 오차의 평균 증가율은 약 83.33% 작아졌고, 드리프트 오차의 최대 증가율은 약 90.73% 작아졌다. 본 논문의 결과는 바이어스 표본을 추출할 때 움직임 없이 기다려야 하는 대기 시간과 정밀도 사이의 관계를 파악하고 표본의 수를 선택하는 근거로써 이용될 수 있다.
Abstract
Gyro sensors present a problem, known as drift error, due to the underlying principle by which they estimate rotation angles. This paper reviews the effect that the number of samples used for bias estimation have on the drift error of a gyro sensor. To this end, the drift error was repeatedly measured for five different sample number conditions.; the results are then compared and evaluated. Results of this experiment indicate that the drift error increase rate is lower when the number of samples for estimating the bias is larger. In particular, when the number of samples was increased from 10 to 1,000, the average increase rate in drift error decreased by about 83.33%, and the maximum increase rate in drift error decreased by about 90.73%. These results can be used as a reference to select the appropriate number of samples, by identifying the relationship between precision and calibration time.
Keywords:
gyro sensor, bias estimation, drift error, motion tracking, inertial measurement unitⅠ. 서 론
사람의 움직임을 감지하고 이용하는 정보기술(IT, Information Technology) 기기들이 늘고 있다. 최근 시판되고 있는 가상 현실(VR, Virtual Reality)용 머리 부분 탑재형 디스플레이(HMD, Head Mounted Display)는 사람의 머리 움직임을 감지하여 그에 맞춘 영상을 실시간으로 변경하고 출력한다[1]-[3]. 또한 최신 비디오 게임기는 기울기나 회전과 같은 사용자의 손의 움직임을 감지하고 게임 제어에 활용한다[4]. 이처럼 사람의 움직임을 감지하고 그에 맞추어 동작하는 장치들은 사용자에게 새롭고 유쾌한 사용자 경험(User experience)을 제공하고 사용자가 더 큰 현실감과 몰입감을 느낄 수 있도록 돕는다[5].
사람의 움직임을 실시간으로 정밀하게 추정하는 방법에는 카메라를 이용한 영상처리 방법, 지자기 센서(Magnetic field sensor)를 이용한 방법, 가속도 센서(Acceleration sensor)와 자이로 센서(Gyroscope)를 이용한 방법 등이 있다[6]-[8]. 이 중 가속도 센서와 자이로 센서를 이용한 방법은 다른 방법에 비해 적은 비용으로 시스템을 구축할 수 있어서 최근 시판되고 있는 개인용 IT 기기에서 널리 이용되고 있다.
자이로 센서를 이용하면 회전 각속도를 측정해 회전각을 추정할 수 있다[8][9]. 회전 각속도를 일정 시간 간격으로 측정하고 측정된 회전 각속도에 측정에 걸린 시간 간격을 곱함으로써 회전량을 추정하고, 이 값을 누적 처리함으로써 회전각을 얻는다. 자이로 센서를 이용한 회전각의 추정 방법은 카메라를 이용한 방법과 지자기 센서를 이용한 방식에 비해 비용이 매우 저렴한 것이 장점이지만, 회전각을 얻기 위해 회전량을 누적시키는 과정에서 측정오차가 누적되어 버리고 누적량은 시간이 지날수록 점점 더 커지게 된다. 이 누적되는 오차를 드리프트 오차(Drift error)라고 한다[8]-[11]. 누적 처리를 이용하는 원리상 드리프트 오차는 필연적으로 발생한다. 따라서 일부 응용 분야에서는 드리프트 오차를 일정 시간마다 초기화시키기 위해서 나침반 센서(Compass sensor)나 소수의 카메라를 함께 사용하는 방법이 이용되고 있다[8][9].
자이로 센서에서 측정되는 회전 각속도에는 바이어스(Bias)가 포함된다[8][9]. 따라서 자이로 센서를 사용할 때는 시스템 초기화 단계에서 자이로 센서의 회전 각속도의 바이어스를 미리 추정해 두고, 추후 각속도를 측정할 때 바이어스를 제거해야 한다. 바이어스를 추정하는 방법의 하나는 자이로 센서가 움직이지 않는 상태에서 회전 각속도의 표본을 다수 측정하고 표본의 평균값을 바이어스 추정치로 사용하는 것이다[8][9].
표본에 포함된 잡음의 영향을 충분히 줄이기 위해서는 평균치를 구하기 위한 표본의 수가 충분해야 한다. 그러나 센서를 사람의 몸에 부착하여 사용하는 경우, 표본 수집을 위해 사용자의 몸을 오랫동안 움직이지 못하게 통제하는 것은 매우 어렵다[7][8]. 따라서 사용 용도, 프로세서의 성능, 자이로 센서의 갱신율 등과 같이 다양한 요소를 통합적으로 고려하여 표본의 수를 얼마만큼 사용할 것인지를 선택해야 한다. 만일 처리에 이용하는 프로세서의 성능이 낮거나 장치의 초기화 시간이 아주 빨라야 하는 경우가 아니라면 더 많은 양의 표본을 수집하는 것이 바이어스를 정밀하게 추정하는 데 도움이 될 것이다. 이러한 중요성에도 불구하고 표본 수와 실제 성능 사이의 실험적 검토 결과는 보고되지 않았다[8].
본 논문에서는 회전 각속도의 바이어스 추정을 위해 필요한 표본의 수가 자이로 센서의 드리프트 오차에 미치는 영향에 대하여 검토한다. 이를 위해 표본의 수를 바꾸어 가면서 드리프트 오차를 측정하고 비교 평가하는 실험을 실시한다. 표본의 수가 많아지면 드리프트 오차의 크기는 더 작아질 것으로 기대되지만 다수의 표본을 수집하는 데에는 더 많은 시간이 필요하다. 이때 센서는 움직이지 않고 정지된 상태여야 하므로 무한정 표본의 수를 늘릴 수도 없다[8]. 따라서 본 논문의 검토 결과는 표본의 수를 어떻게 선택하는 것이 적절한가를 판단하는데 활용될 수 있다.
본 논문의 구성은 다음과 같다. 2장에서는 측정 실험에서 사용하는 자이로 센서를 이용한 회전각 측정시스템에 대하여 설명한다. 3장에서는 측정 실험의 방법에 대하여 설명한다. 4장에서는 측정 실험의 결과를 고찰한다. 마지막 5장은 결론 및 향후 과제이다.
Ⅱ. 자이로 센서를 이용한 회전각 측정시스템
측정 실험에서 사용하는 자이로 센서를 이용한 회전각 측정시스템의 하드웨어 구성 및 측정 원리에 대하여 설명한다. 하드웨어 구성은 크게 자이로 센서 모듈, 마이크로 컨트롤러 보드, 컴퓨터로 분류된다.
본 논문에서 구현한 회전각 측정시스템의 외관을 그림 1에 나타낸다. 자이로 센서 모듈(MPU6050)과 마이크로 컨트롤러 보드(Arduino nano)는 가로세로 모두 5cm인 소형 인쇄회로기판(PCB, Printed Circuit Board)의 윗면과 아랫면에 각각 견고히 납땜하여 부착하였다[12]. 본 논문에서 사용한 자이로 센서 모듈인 MPU6050의 주요 규격을 표 1에 나타낸다[13].
자이로 센서 모듈은 수평 회전 각속도를 실시간으로 갱신한다. 자이로 센서와 마이크로 컨트롤러 보드는 I2C(Inter-Integrated Circuit) 통신을 통해 연결되고, 마이크로 컨트롤러 보드가 요청하면 자이로 센서 모듈은 실시간으로 갱신하고 있던 회전 각속도의 미가공 데이터(Raw data)를 송신한다. 마이크로 컨트롤러 보드는 미가공 데이터를 수신한 후, 처리 알고리즘을 이용해 회전각을 추정한다.
컴퓨터(Windows PC)는 마이크로 컨트롤러 보드와 UART(Universal Asynchronous Receiver/Transmitter) 통신으로 연결된다. 컴퓨터가 마이크로 컨트롤러 보드에 회전각의 전송을 요청하면 마이크로 컨트롤러 보드는 회전각을 전송한다. 마이크로 컨트롤러 보드와 컴퓨터를 제어하기 위한 프로그램은 모두 C++ 언어를 이용해 작성하였다.
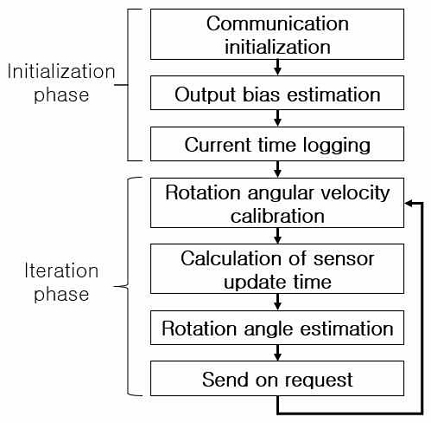
마이크로 컨트롤러 보드는 그림 2와 같은 처리 흐름으로 회전각을 추정하고 컴퓨터의 요청 시 회전각을 전송한다. 회전각 측정시스템의 처리 흐름은 크게 초기화 단계와 반복 처리 단계로 나뉜다.
초기화 단계에서 마이크로 컨트롤러 보드는 먼저 자이로 센서 모듈과의 I2C 통신을 초기화하고, 컴퓨터와의 UART 통신을 초기화한다. UART 통신을 위한 보 레이트(Baud rate)는 115200을 사용하였다.
자이로 센서의 출력 바이어스는 식 (1)과 같이 얻어진다[8][9].
| (1) |
여기에서 Zraw (i) (i=1,2,⋯,N)는 자이로 센서를 움직이지 않도록 통제한 상태에서 수집한 자이로 센서의 +Z축에 대한 회전 각속도의 미가공 데이터의 표본이다. 표본의 수는 N개이고, Zbias는 Zraw (i)의 평균값이다.
초기화 단계의 마지막은 현재 시각을 저장하는 것이다. 이 값은 이어지는 반복 처리 단계의 센서 갱신 시간 산출에 이용된다.
반복 처리 단계에서는 자이로 센서로부터 수신한 회전 각속도의 미가공 데이터를 아래와 같이 교정한다[8][9].
| (2) |
여기에서 Zraw (n)은 I2C 통신을 통해 자이로 센서로부터 수신한 회전 각속도의 미가공 데이터이고, Zbias는 식 (1)에서 얻어진 자이로 센서의 출력 바이어스이다. Zcalib (n)은 교정된 수평 회전 각속도이고, 단위는 deg/s이다.
| (3) |
여기에서 tnow (n)은 현재 시각이고, tprev (n)은 반복 처리의 직전 단계에서 저장해 둔 시각이다. 단, 최초 1회의 경우 tprev (n)는 초기화 단계의 마지막에서 저장해 둔 시각이다. Δt(n)은 센서의 갱신 시간이고, 단위는 s이다.
수평 회전각은 식 (2)와 식 (3)을 이용해 아래와 같이 얻어진다[8][9].
| (4) |
여기에서 Yaw (n-1)은 반복 처리의 직전 단계에서 구한 수평 회전각을 나타내고, Yaw (n)은 최신 수평 회전각이다. 수평 회전각의 초기값은 0도이다.
반복 처리 단계의 마지막은 컴퓨터로부터 수신된 전송 요청 메시지의 유무를 확인하고 요청이 있었다면 회전각을 전송한다. 컴퓨터로부터 수신되는 전송 요청 메시지는 1바이트의 약속된 값을 이용하였다. 마이크로 컨트롤러 보드에서 컴퓨터로 송신하는 메시지는 총 3바이트로, 1바이트의 약속된 값을 갖는 헤더(Header) 데이터와 2바이트의 부동 소수점 방식의 실수 데이터로 이루어진다.
Ⅲ. 측정 실험
바이어스 추정을 위한 표본의 수가 자이로 센서의 드리프트 오차에 미치는 영향을 검토하기 위해서 측정 실험을 진행한다. 이를 위해 표본의 수를 바꾸어 가면서 일정 시간 동안 회전각을 추정하고 컴퓨터로 전송한다. 컴퓨터에서는 수신한 값을 저장하고 이 값을 이용해 드리프트 오차의 발생 경향을 비교 분석한다.
실험 조건을 표 2에 나타낸다. 바이어스 추정을 위한 표본의 수는 10개, 50개, 100개, 500개, 1,000개로서 총 5가지 조건에 대하여 실험을 진행한다. 표본의 수는 식 (1)의 N을 나타낸다. 표본의 수집 간격은 약 5ms이다.
자이로 센서의 출력 바이어스를 추정하기 위해 회전 각속도의 미가공 데이터 표본을 수집할 때는 센서가 움직이지 않도록 주의해야 한다. 센서가 움직이게 되면 바이어스만이 출력되지 않고, 움직임에 의한 회전 각속도가 포함되어 버리기 때문이다.
선행 연구에서는 표본의 수로 10개를 이용하였다[8][9]. 이 경우 10개의 표본을 수집하는 데 약 50ms가 소요된다.
반면에 100개를 수집하는 데 약 0.5s, 1,000개를 수집하는 데 약 5s가 소요된다. 예를 들어 사람과 같이 움직임을 장시간 통제하기 어려운 대상의 몸에 부착하고 표본을 수집할 때 5s는 너무 긴 시간이다. 반면에 움직임이 없는 사물에 부착한 상태라면 5초간 표본을 수집하는 것도 어렵지 않을 것이다. 따라서 자이로 센서를 사용하고자 하는 대상과 표본 수집 시점에서 대상의 움직임을 얼마간 통제할 수 있는지를 종합적으로 고려하여 표본의 수를 선택해야 한다.
이와 같은 이유로 본 실험에서는 선행 연구의 표본 수인 10개를 포함하여 사람에게 부착한 상태에서도 크게 문제가 되지 않을 것으로 생각되는 1초 이내의 대기 시간에 해당하는 3가지 조건(10, 50, 100)과 사람에게 부착한 상태에서는 사용하기 어렵지만 움직임이 없는 사물에 대해서는 사용할 수 있을 것으로 생각되는 2가지 조건(500, 1000)을 실험 조건으로 선정하였다.
컴퓨터는 표본 수의 5가지 조건에 대하여 반복 처리 단계에서 추정된 회전각을 약 15ms 간격으로 4,000회 수신한다. 수신한 값을 이용해 각 조건에서의 드리프트 오차의 발생 경향을 비교 분석한다. 측정 실험은 각 조건에 대하여 5회 반복 수행하였다.
Ⅳ. 실험 결과 및 고찰
자이로 센서의 움직임을 통제한 상태에서 출력 바이어스를 추정하고, 이후 자이로 센서를 계속해서 움직이지 않게 유지한 상태에서 회전 각속도를 교정하고 회전각을 추정하면 드리프트 오차를 확인할 수 있다. 출력 바이어스가 완벽히 제거되었다면, 자이로 센서가 움직이지 않을 때 회전각의 추정치는 일정한 값을 유지해야 한다[8]. 그러나 바이어스를 완벽히 제거하는 것은 매우 어렵다. 따라서 자이로 센서가 움직이지 않는데도 시간의 흐름과 함께 회전각의 크기는 조금씩 변화하고, 이때 목표 회전각과의 차이가 드리프트 오차이다[8]-[11].
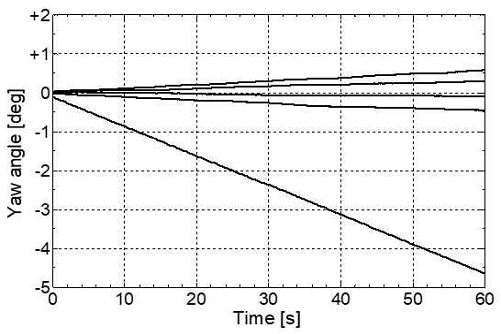
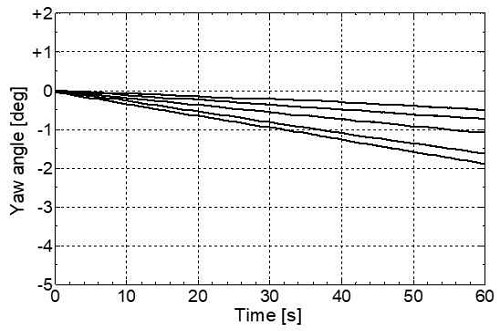
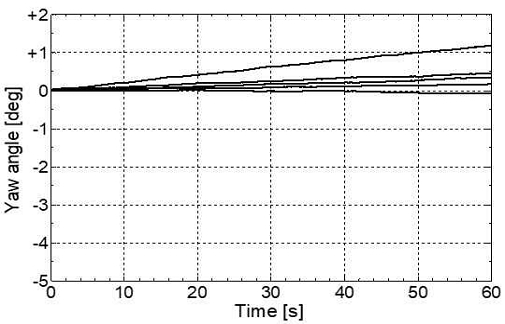
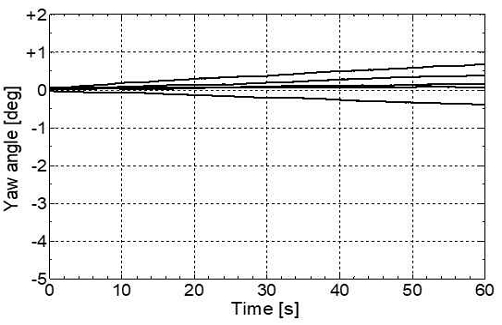
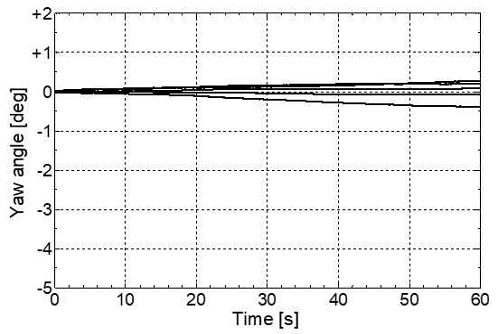
표본 수의 5가지 조건에 대하여 자이로 센서를 움직이지 않게 고정한 후 회전각 추정치의 변화를 확인하였다. 각 조건에 대한 추정치의 변화를 그림 3부터 그림 7까지 각각 나타낸다. 모든 그림에서 가로축은 시간을 나타내고 단위는 초(s)이다. 세로축은 추정된 회전각의 크기를 나타내고 단위는 도(deg)이다. 세로축의 0도는 정면을 나타내고, +쪽은 +Z축에 대하여 시계 반대 방향으로 회전한 것을, -쪽은 시계방향으로 회전한 것을 의미한다.
결과로부터 회전각의 변화추이는 시계방향과 반시계 방향 어느 쪽으로도 발생할 수 있다는 것을 알 수 있다. 또한, 표본의 수가 더 적을수록 회전각의 변화폭이 더 넓고, 표본의 수가 더 많을수록 회전각의 변화폭이 더 작은 것을 알 수 있다.
그림 3부터 그림 7까지 모두에서 움직임이 없는데도 불구하고 회전각의 크기가 점점 커지거나 작아지는 것을 볼 수 있다. 표본의 수가 증가하면 증가하는 속도를 늦출 순 있지만, 결국 오차는 점점 더 커진다. 이처럼 누적 처리를 이용하는 원리상 드리프트 오차는 필연적으로 발생한다. 따라서 자이로 센서를 이용할 때에는 응용 분야에 따라서 누적된 드리프트 오차가 영향을 주지 않는 범위에서만 주의해서 사용해야 한다.
만약 회전각을 정밀하게 유지해야 하는 응용 분야라면 나침반 센서나 카메라 등의 센서와 함께 사용하여 드리프트 오차를 정밀하게 제거해주는 처리를 병행해야 할 것이다[8][9].
이상적인 회전각의 방향은 정면인 0도를 가리켜야 한다. 따라서 그림의 회전각에 대하여 절댓값을 취한 것을 드리프트 오차라고 생각할 수 있다. 또한 회전각의 절댓값의 기울기는 드리프트 오차의 증가율로 생각할 수 있다. 더욱 정밀한 분석을 위해 그림 3부터 그림 7까지의 회전각 데이터에 대하여 절댓값을 취해 드리프트 오차로 변환하고, 드리프트 오차의 기울기를 선형 최소제곱 회귀(Linear least-squares regression)를 통해 추정하였다[8][14]. 추정된 드리프트 오차의 기울기는 오차의 증가율을 의미한다. 또한, 회귀 분석의 결과가 데이터를 얼마나 잘 설명하는지를 나타내는 결정 계수(Coefficient of determination) R2도 함께 산출하였다[8][14].
표본 수의 5가지 조건에 대하여 추정한 드리프트 오차의 회귀 계수를 표 3부터 표 7에 각각 나타낸다. 표에서 Intercept는 회귀 분석을 통해 얻은 직선의 y절편을 나타내고 단위는 도(deg)이다. Slope는 직선의 기울기를 나타내고 단위는 deg/sec이다. Coefficient of determination은 결정 계수이다. Average는 총 5회의 반복 실험에 대한 평균값을, Standard error는 표준오차를 나타낸다. 그림 3부터 그림 7까지의 회전각을 절댓값을 취해 드리프트 오차로 변환하고 회귀 분석을 통해 기울기를 구했기 때문에 기울기를 나타내는 Slope는 모두 양수이다.
표에서 표본의 수가 더 적을수록 드리프트 오차의 평균 기울기가 더 크고, 표본의 수가 더 많을수록 드리프트 오차의 평균 기울기가 더 작다는 것을 알 수 있다. 기울기는 오차의 증가율을 뜻하므로 표본의 수가 더 많을수록 드리프트 오차가 더 적게 증가한다고 해석할 수 있다.
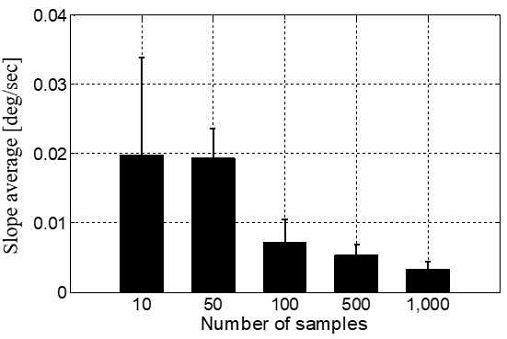
표본의 수에 따른 드리프트 오차의 평균 증가율을 그림 8에 나타낸다. 그림에서 가로축은 표본의 수를 나타내고, 세로축은 드리프트 오차의 평균 증가율을 나타낸다. 이값은 표 3부터 표 7까지의 Slope의 평균값을 비교한 것이다. 오차 범위는 표의 Standard error이다. 그림 8에서 표본 수가 더 많을수록 드리프트 오차의 평균 증가율이 더 작아진다는 것을 알 수 있다. 표본의 수가 10일 때 드리프트 오차의 평균 증가율은 0.0198이지만, 표본의 수가 1,000으로 증가하면 약 16.67%에 해당하는 0.0033으로 작아진다.
또한, 표본 수가 더 많을수록 Standard error가 더 작은 것으로부터 반복 수행에 따른 재현율이 더 크다는 것을 알 수 있다. 표본의 수가 10일 때 Standard error는 0.0140이지만, 표본의 수가 1,000으로 증가하면 약 7.14%에 해당하는 0.0010으로 작아진다.
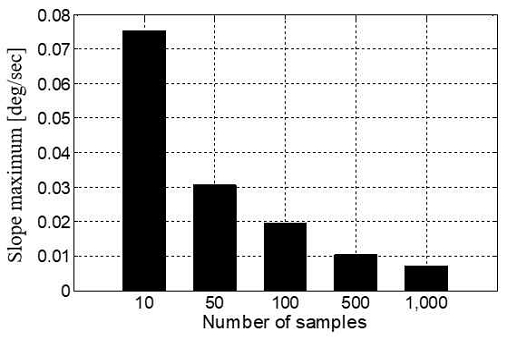
오차의 비교에 있어서는 평균값의 검토뿐만 아니라 최댓값에 대한 검토도 필요하다. 표본의 수에 따른 드리프트 오차의 최대 증가율을 그림 9에 나타낸다. 이값은 표 3부터 표 7까지의 Slope의 최댓값을 비교한 것이다. 그림 9에서 표본의 수가 더 많을수록 드리프트 오차의 최대 증가율이 더 작아진다는 것을 알 수 있다. 표본의 수가 10일 때 드리프트 오차의 최대 증가율은 0.0755이지만, 표본의 수가 1,000으로 증가하면 약 9.27%에 해당하는 0.0070으로 작아진다.
이상의 실험 결과로부터 바이어스를 추정하기 위한 표본의 수가 많을수록 드리프트 오차의 증가율을 더 작게 억제할 수 있음을 알 수 있다. 선행 연구에서는 바이어스 추정 시 표본의 수를 10개로 하였는데[8][9], 이번 검토에 의하면 표본의 수를 더 늘림으로써 정밀도를 높일 수 있을 것으로 기대된다. 그러나 표본의 수는 바이어스 추정 시 움직이지 않도록 통제해야 하는 시간과 비례하기 때문에, 응용 분야에 따라서는 표본의 수를 무한정 늘리는 것이 좋지 않은 선택일 수 있다. 예를 들어, 1,000개의 표본을 5ms 간격으로 수집하는 데 5초가 필요한데 사람의 움직임을 5초 동안 통제하는 것은 매우 어렵다. 따라서 응용 분야마다 적절한 대기 시간을 고려해 표본의 수를 선택할 필요가 있다.
한편, 더 빠른 프로세서와 갱신율이 높은 자이로 센서 모듈을 사용한다면 표본 간격을 줄여 표본 수를 늘리는 것이 가능할 수 있다. 표본 수집 간격을 조절하면 대기 시간은 같으면서도 더 많은 표본을 수집할 수 있으므로 드리프트 오차의 증가율은 감소할 가능성이 있다.
또한, 이번에 사용한 마이크로 컨트롤러는 초소형으로 작은 시스템을 만들기에는 적합하지만, 성능이 매우 우수한 편은 아니었고 2바이트의 부동 소수점 방식의 실수 데이터를 지원하였다. 따라서 더 빠르고 더 큰 정밀도를 지원하는 마이크로 컨트롤러를 이용한다면 보다 정밀한 검토가 가능할 것으로 생각된다.
덧붙여, 실수 데이터는 근사치를 저장하는 방식이기 때문에 자이로 센서에서 전송된 정수형의 미가공 데이터에 대하여 실수형 계산을 최대한 늦추는 형태로 최적화한다면 오차의 발생량을 억제할 가능성이 있다고 생각된다.
Ⅴ. 결론 및 향후 과제
자이로 센서를 이용하면 사물의 회전각을 쉽게 추정할 수 있지만, 회전각을 추정하는 원리상 드리프트 오차라고 하는 피할 수 없는 문제를 갖는다.
본 논문에서는 바이어스 추정을 위한 표본의 수가 자이로 센서의 드리프트 오차에 미치는 영향을 검토하였다. 이를 위해 5가지 조건을 선정하고 표본의 수를 바꾸어 가면서 드리프트 오차를 측정하고 비교 평가하는 실험을 반복 수행하였다. 실험 결과, 바이어스를 추정하기 위한 표본의 수가 더 많을수록 드리프트 오차의 증가율이 감소한다는 사실을 알 수 있었다. 특히, 표본의 수를 10에서 1,000으로 증가시켰을 때, 드리프트 오차의 평균 증가율은 약 83.33% 작아졌고, 드리프트 오차의 최대 증가율은 약 90.73% 작아졌다.
본 논문에서는 표본 수집 간격으로 1가지 조건만을 이용하였지만, 표본 수집 간격을 작게 하면 같은 대기 시간 동안 더 많은 표본을 확보할 수 있으므로 이로 인해 드리프트 오차의 증가율이 감소할 가능성이 있다. 또한, 더 빠르고 더 큰 정밀도를 지원하는 마이크로 컨트롤러를 이용한다면 보다 정밀한 검토가 가능할 것으로 생각된다. 이상의 추가적인 검토를 본 논문의 향후 과제로 한다.
References
-
H. Moon and S. Chung, "Quantitative Evaluation Method of Unilateral Neglect based on K-CBS using Virtual Reality", Journal of IIBC, Vol. 20, No. 1, pp. 141-148, Feb. 2020.
[https://doi.org/10.7236/JIIBC.2020.20.1.141]

-
B. Kang and S. Lee, "Tele-operation System of Unmaned Fire Truck for Real-time Fire Suppression", Journal of IIBC, Vol. 22, No. 6, pp. 1-6, Dec. 2022.
[https://doi.org/10.7236/JIIBC.2022.22.6.1]

- D. Jeong, "Latest technology trends and prospects for virtual reality", The Korea Multimedia Society Review, Vol. 20, No. 4, pp. 1-8, Dec. 2016.
- Q. Le, Y. Jeong, C. Nguyen, and S. Yang, "Study on Remote Control for Field Robot and Augmented Reality Vision Using Head Tracker System", Proc. of KSFC Autumn Conference, pp. 65-70, Sep. 2014.
-
W. Jung, "A study on user input/output response time to improve user experience of goggle-type AR drone contents", Journal of Korea Game Society, Vol. 23, No. 2, pp. 3-12, Apr. 2023.
[https://doi.org/10.7583/JKGS.2023.23.2.3]

-
D. Chwa, "Motion Estimation of a Moving Object in Three-Dimensional Space using a Camera", The Transactions of the Korean Institute of Electrical Engineers, Vol. 65, No. 12, pp. 2057-2060, Dec. 2016.
[https://doi.org/10.5370/KIEE.2016.65.12.2057]

-
T. Hirahara, H. Sagara, I. Toshima, and M. Otani, "Head movement during head-related transfer function measurements", Acoust. Sci. and Tech., Vol. 31, No. 2, pp. 165-171, Mar. 2010.
[https://doi.org/10.1250/ast.31.165]

-
C. Han and H. Kim, "A Real-time Yaw Rotation Angle Measurement System for Human Heads Using a Gyro Sensor", Journal of KIIT, Vol. 15, No. 8, pp. 59-66, Aug. 2017.
[https://doi.org/10.14801/jkiit.2017.15.8.59]

- M. Seo, "Build an Arduino drone and code it yourself", Answerbook, Apr. 2016.
-
M. Wu and X. Yin, "Research on Gyro Drift Two Position Calibration Method for Vehicle Strap-down Inertial Navigation System", ICEDME, pp. 706-709, May 2020.
[https://doi.org/10.1109/ICEDME50972.2020.00166]

-
Y. Tu and C. Peng, "An ARMA-Based Digital Twin for MEMS Gyroscope Drift Dynamics Modeling and Real-Time Compensation", IEEE Sensors Journal, Vol. 21, No. 3, pp. 2712-2724, Feb. 2021.
[https://doi.org/10.1109/JSEN.2020.3028140]

- Arduino Nano, https://store.arduino.cc/products/arduino-nano, . [Accessed: Jun. 21, 2023]
- MPU-6050, https://invensense.tdk.com/products/motion-tracking/6-axis/mpu-6050, . [Accessed: Jun. 21, 2023]
-
D. A. Freedman, "Statistical Models: Theory and Practice", Cambridge University Press, Apr. 2009.
[https://doi.org/10.1017/CBO9780511815867]


2006년 2월 : 청주대학교 전자공학과(공학사)
2008년 2월 : 청주대학교 대학원 전자공학과(공학석사)
2013년 9월 : 일본 도호쿠대학 대학원 정보과학연구과(공학박사)
2013년 9월 ~ 2015년 8월 : 청주대학교, 한국교통대학교 시간강사
2015년 9월 ~ 현재 : 청주대학교 전자공학과 교육전담 조교수
관심분야 : 신호처리, 알고리즘, 프로그래밍