TFT 모델 및 진동 신호 분해 기반 모터 구동 설비의 상태 모니터링 및 이상 탐지

Ⅰ. 서 론

최근 제조기업들은 생산성 향상과 비용 절감 및 제품의 품질 향상을 위해 스마트 공장 구축에 큰 관심을 기울이고 있다. 스마트 공장은 사물인터넷(IoT), 클라우드 컴퓨팅, 로봇, 빅데이터 분석, 인공지능 등 첨단 기술을 활용하여 기존의 공장을 디지털화하는 과정으로, 제품 생산 과정에 사용되는 복잡하고 다양한 설비에 지능화된 관리 기술이 도입된다. 즉, 설비 관리자들은 설비에 부착된 센서로부터 데이터를 수집함으로써 공정 상태를 모니터링하고 성능을 최적화할 수 있다. 또한, 설비의 이상을 조기에 발견하고, 결함의 원인을 분석하여 심각한 고장이나 갑작스러운 가동 중단을 미리 예방할 수 있다. 이러한 설비 관리 기술은 설비의 현재 상태를 파악하고 문제점을 진단하여 필요한 부분에 대한 사전 정비를 수행하는 예지 보전(Predictive maintenance)을 위해 필수적인 기술로 최근 활발한 연구가 이루어지고 있다[1].

설비의 상태 모니터링과 이상 탐지 및 문제점 진단을 위한 핵심 기술은 시계열 데이터 분석 및 예측이다. 시계열 데이터 예측은 과거의 데이터에 기반해 미래의 변수 값을 예측하는 기술로 여러 분야에서 활용도가 높아 통계 기반 예측 모델로부터 머신러닝 및 딥러닝 예측 모델에 이르기까지 다양한 연구가 이루어졌다. ARIMA(Auto-Regressive Integrated Moving Average)는 대표적인 통계 기반 시계열 예측 모형으로 통계적 특징이 시간에 따라 변화하는 비정상(Non-stationary) 시계열을 차분을 통해 정상화시켜 예측 성능을 높인다[2]. LSTM(Long Short-Term Memory)은 시계열 데이터의 장기 의존성을 학습할수 있는 순환신경망으로 시계열 예측에 활용되는 대표적 딥러닝 모델이다[3]. 학습 데이터가 비교적 적을 경우 예측 속도가 빠르고 해석이 용이한 XGBoost[4]나 LightGBM[5]과 같은 결정트리 앙상블 기반의 머신러닝 모델도 자주 사용된다. 최근 제안된 TFT(Temporal Fusion Transformer)[6]는 Transformer[7] 구조를 도입하여 시계열 데이터 특징의 학습 성능을 높이고 여러 환경 변수를 효과적으로 학습할 수 있는 구조를 가진 딥러닝 기반 예측 모델로 다양한 분야에서 우수한 예측 성능을 보여주고 있다[8]-[14].

제조업에서 회전력을 이용해 기계를 동작시키는 모터는 거의 전 제조 분야에 사용되는 핵심 설비로 모터 설비의 고장이나 이상은 생산성 저하 및 작업 안전과 직결될 수 있다. 또한, 모터는 물리적인 회전력을 생성하므로 기계 장치와 연결되어 진동, 마모, 과열 등 성능이나 수명을 저하시킬 수 있으므로 모터 구동 설비의 상태에 대한 철저한 관리가 필요하다. 본 논문은 이렇게 제조업에서 가장 중요한 예지 보전 대상인 모터 구동 설비의 상태 모니터링 및 이상 탐지 시스템을 제시한다. 제안하는 시스템은 모터를 통해 작동되는 기계 설비에 진동 정보를 제공하는 3축 가속도 센서가 포함된 스마트 센서를 부착하여 상태 데이터를 수집하고 가속도 센서 값의 예측을 기반으로 설비의 상태 및 이상 여부를 파악한다. 모터 구동 설비의 상태 분석을 위한 시계열 예측의 정확성을 확보하기 위해 우수한 예측 성능을 보여주고 있는 TFT를 시계열 예측 모델로 사용한다. 또한 진동 신호의 효과적인 학습을 위해 신호 분해 기법을 통해 진동 신호를 분해한 데이터를 모터 구동 설비의 제어 신호와 함께 학습 데이터로 활용한다. 모터 구동 설비의 경우 대부분 모터의 회전력을 이용해 기계 장치가 빠르게 동작하기 때문에 진동 특성 정보를 확보하기 위해서는 초당 수십 개 이상의 센서 데이터를 대량으로 수집하고 학습해야 한다. 제안 시스템은 이러한 요구사항을 만족시킬 수 있도록 고속의 데이터 수집, 실시간 분석 및 모니터링이 가능하도록 설계되었다.

본 논문의 구성은 다음과 같다. Ⅱ장에서는 관련 연구로 제조 설비의 예지보전 시스템 개발 현황 및 사례, TFT 모델 및 관련 연구 동향, 주요 신호 분해 기법에 대해 기술한다. Ⅲ장에서는 본 논문에서 제안하는 모터 구동 설비의 상태 모니터링 및 이상탐지 시스템과 설비 상태의 분석 알고리즘을 설명한다. Ⅳ장에서는 모델 학습 및 추론 환경, 시각화 웹 플랫폼 등 제안 시스템 구현 방법에 대해 소개한다. Ⅴ장에서는 제안하는 시스템의 예측 성능에 대해 평가 결과를 제시하고, 마지막 Ⅵ장에서 결론 및 향후 연구에 대하여 기술한다.

Ⅱ. 관련 연구

2.2 TFT(Temporal Fusion Transformer)

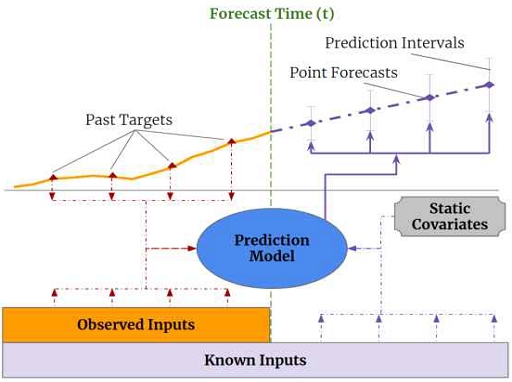
TFT는 Transformer 기반의 시계열 예측 모델로 self-attention을 활용하여 다중 시계열의 복잡한 시간적 변화의 특성을 추출할 수 있다. TFT는 그림 1에서 볼 수 있는 것처럼 다변수 시계열 데이터와 시간 가변 및 정적 변수, 관찰 변수 및 사전 인지 변수 등 이종(Heterogeneous) 데이터를 효과적으로 학습하여 예측 대상 변수의 다중 시간 예측(Multi-horizon forecasting) 성능을 향상시켰다.

Fig. 1.

Heterogeneous data training and multi-horizon forecasting of the TFT[6]

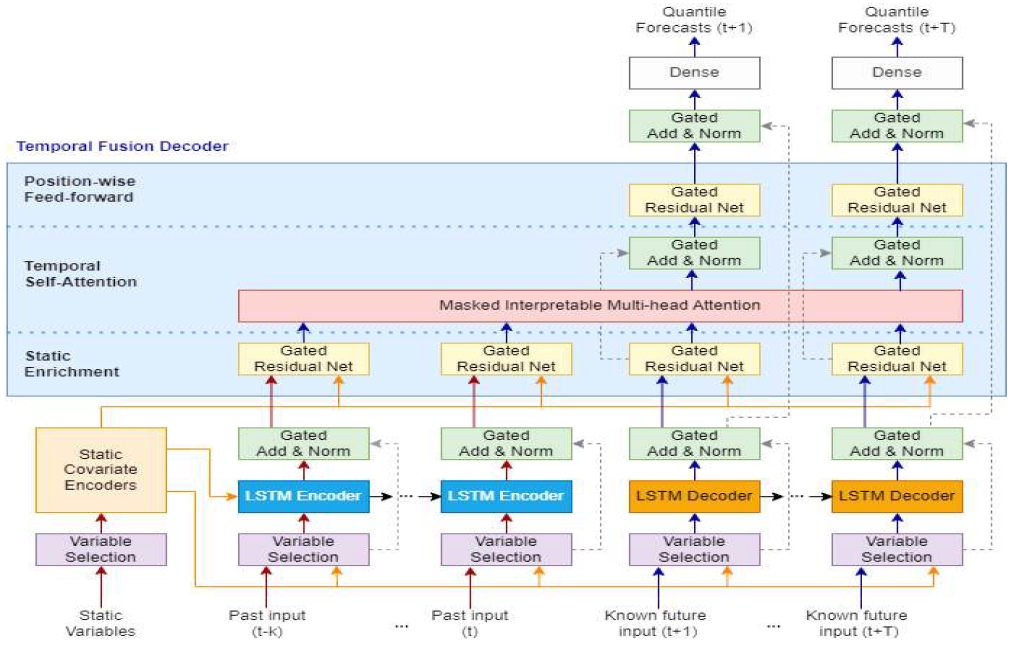
그림 2는 TFT 모델의 전체 구조를 보여준다. 시계열 데이터의 관찰 변수의 과거 데이터는 LSTM 인코더에 입력되고 사전 인지 변수 데이터는 미래 시점의 LSTM 디코더에 입력된다. 정적 변수 데이터는 과거와 미래에 모두 동일하므로 LSTM 인코더, 디코더 및 TF(Temporal Fusion) 디코더 전체에 전달된다.

Fig. 2.

Architecture of the TFT model[6]

이때 각 변수는 변수 선택 모듈을 거치며 가중치가 부여된다. LSTM 인코더, 디코더를 통과한 입력 데이터는 TF 디코더의 핵심인 마스킹된 해석 가능 다중헤드 어텐션 계층(Masked interpretable multi-head attention layer)에 전달되어 입출력 데이터의 시간적 연관성이 셀프 어텐션(Self-attention) 기반으로 학습된다. 어텐션 계층에서 산출된 정보는 일련의 게이팅(Gating) 처리과정을 거쳐 분위수(Quantile) 기반 예측 결과를 제공하게 되는데 이때 LSTM 디코더의 출력 정보를 반영한다. 게이팅 메커니즘은 네트워크의 복잡성을 완화하기 위해 모델 전체에서 사용되고 있다.

TFT 모델은 최근 보건, 교통, 기상(Weather), 발전(Power generation) 등 다양한 분야에 적용되어 기존 모델 대비 우수한 예측 성능을 보여주고 있다[8]-[14]. 주요 적용 예로는 Covid-19 환자 수 예측[8], 응급실 혼잡도 예측[9], 항공기 지연 예측[10], 일일 최대 강수량 예측[11], 풍력 발전량 예측[12][13], 원자로 사고 예후를 예측[14] 등이 있다. 이러한 사례의 공통점은 시계열 데이터의 시간 단위가 대부분 하루 또는 한 시간으로 비교적 길다는 점이다. 초당 수회에서 수십회의 센서 데이터 측정을 사용하는 제조 설비의 예지 보전 분야에 적용된 사례는 아직 찾을 수 없었다.

2.3 신호분해 기법

센서에서 수집되는 데이터는 시간에 따라 측정 값이 변화하는 시계열 데이터로 예측 모델은 데이터의 시간적 변화에 존재하는 특징 정보를 학습하게 된다. 그러나 노이즈 등 외부적 간섭 요인으로 인해 시계열 데이터의 변화 패턴이 매우 복잡할 경우 데이터의 특징 추출이 쉽지 않게 된다. 이 경우 머신러닝에서의 데이터 전처리와 유사한 개념으로 시계열 데이터에 존재하는 특징 정보를 사전에 추출하여 학습 데이터로 활용할 수 있다. 특히 제조 설비의 경우 진동 데이터가 모터의 회전에 의해 매우 특징적인 주파수 대역의 정보를 가질 수 있기 때문에 데이터 분석을 위해 신호의 분해 기법이 자주 사용되었다.

가장 대표적인 신호 분해 기법으로 시간 영역 데이터를 주파수 영역 데이터로 변환하는 푸리에 변환(FT, Fourier Transform)이 있다.

푸리에 변환은 설비의 상태를 특정 주파수 대역의 정보로 포착할 수 있을 때 매우 유용한 방법이나 변환된 주파수 영역 데이터에는 시간 정보가 존재하지 않으므로 시계열 예측 모델에 직접 적용하기가 용이하지 않다. STFT(Short Time Fourier Transform)는 시계열 데이터의 시간 구간을 짧게 나누고 나누어진 각 구간의 신호를 푸리에 변환하는 방법으로, 시간에 따라 특성이 변하는 신호를 분석하는데 활용될 수 있다[21]. 웨이블릿 변환(WT, Wavelet Transform)은 시간 영역 신호를 웨이블릿 신호의 집합으로 구성하는 것으로 시간과 주파수 영역 정보를 동시에 분석할 수 있으나 분석할 주파수 대역을 사전에 파악해야 한다.

EMD(Empirical Mode Decomposition)는 복잡한 신호를 IMF(Intrinsic Mode Functions)이라고 부르는 기본 진동 구성 요소로 분해하는 신호처리 기술로 데이터에 기반해 신호를 몇 개의 요소 신호로 분해할 수 있다[22]. 분해된 각 신호는 높은 주파수부터 낮은 주파수까지 다른 진동 스케일을 나타내며 모든 IMF를 추출한 후 얻은 최종 잔여 신호는 원래 신호의 추세(Trend)를 나타낸다. EMD는 원 신호를 여러 개의 시간 영역 신호로 분해하므로 분해된 신호를 시계열 데이터로 직접 활용할 수 있다.

EMD는 한 시간 스케일의 진동이 여러 IMF에 나누어 저장되거나 하나의 IMF에 여러 시간 스케일의 진동이 저장되는 문제가 있고 IMF의 수가 데이터에 따라 달라질 수 있어, 이를 극복하기 위해 개발된 방법이 EEMD(Ensemble EMD)이다[23]. EEMD는 원래 시계열 데이터에 무작위 노이즈를 추가한 후 IMF를 구하는 방법을 여러 번 수행하는 앙상블 방법으로 각 IMF를 추출함으로써 IMF 간 상호작용을 최소화하고 IMF 수를 일정하게 유지할 수 있다. 그러나 EEMD는 계산 비용이 높아져 실시간 변환이 어려울 수 있다.

VMD(Variational Mode Decomposition)는 입력 신호를 FFT(Fast Fourier Transform)[24]를 이용해 주파수 영역으로 변환하고 최적화 과정을 통해 각 주파수 대역별로 IMF를 추정하는 방식을 사용한다[25]. 주파수 영역 변환을 위해 직접 FFT를 사용하므로 EMD보다 잡음에 강하고 분해능이 우수하며 EEMD보다 계산 비용이 적다는 장점이 있다. 한편, MSTL(Multiple Seasonal-Trend decomposition using LOESS)[26]과 같이 시계열 데이터를 계절성(Seasonal) 반복 요소, 추세, 및 잔여 요소로 분해하는 통계적 기법도 있다. 표 1은 각 신호 분해 기법의 특징을 비교하여 보여준다.

Table 1.

Comparisons of signal decomposition methods

최근 시계열 데이터 예측에 신호 분해 기법을 사용하는 연구가 제안되고 있다. W-Transformer는 시계열 데이터를 WT를 이용해 분해한 후 각 분해 신호에 대해 Transformer를 이용해 예측을 수행한 후 다시 역 WT를 수행하여 시계열 신호로 변환하는 방식을 제안한다[27]. [11][12]는 풍력발전량 예측을 위해 발전량 데이터와 함께 신호 분해 기법으로 분해된 신호를 학습에 사용했을 때 예측성능이 향상되었음을 보였다.

Ⅲ. 제안 시스템

3.1 전체 시스템 구조

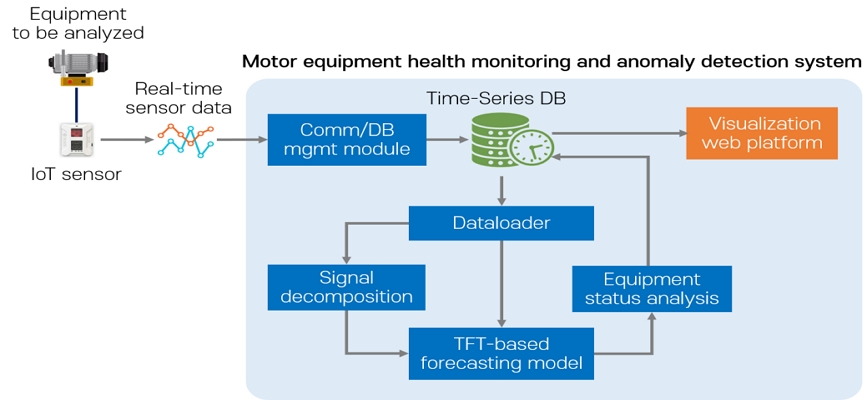
제안하는 모터 구동 설비의 상태 모니터링 및 이상탐지 시스템의 전체 구조는 그림 3과 같다.

Fig. 3.

Architecture of the proposed system

분석 대상인 모터 구동 설비에 부착된 IoT 센서로부터 측정된 시계열 데이터는 무선 신호를 통해 시스템의 통신/DB 관리 모듈에 전송된다. 통신/DB 관리 모듈은 수신된 데이터를 실시간으로 시계열 DB에 저장한다. 센서 데이터는 초당 수십 회까지 고속으로 데이터를 전송하므로 일반적인 관계형 DB보다 시계열 DB가 데이터 처리에 적합하다.

데이터로더는 시계열 DB에 저장된 최신 센서 데이터를 가져와 신호 분해를 수행하고, 센서 데이터와 분해 데이터를 함께 TFT-기반 예측 모델에 입력한다. TFT-기반 예측 모델은 수집된 학습 데이터로 사전 학습된 상태로, 입력된 데이터를 처리하여 예측 대상 신호에 대해 지정된 분위 예측 값을 출력한다. 상태 분석(Equipment status analysis) 모듈은 실제 값과 분위 예측 값을 이용해 규칙 기반으로 모터 설비의 상태 분석 및 이상 탐지를 수행하고, 예측 데이터와 상태 분석 결과를 다시 시계열 DB에 저장한다. 마지막으로 시각화 웹 플랫폼은 시계열 DB에 저장된 모터 설비의 실시간 수집 및 예측 데이터와 상태 분석 결과를 시각화하여 보여준다. 예측 모델의 학습 및 추론에 사용되는 입력 데이터와 상태 분석 모듈에서 사용하는 이상탐지 및 상태 판별 알고리즘은 각각 3.2절과 3.3절에서 상세히 설명한다.

3.3 이상 탐지 및 상태 판별

일반적으로 시계열 데이터 예측을 이용한 이상 탐지 방법은 예측 값과 실제 값과의 차이(절대값 또는 제곱값)를 이상 지수(Anomaly score)로 사용하여 이상 지수가 정해진 문턱 값을 초과할 경우 이상 상황으로 간주하는 방식을 사용한다. 그런데 TFT 모델은 현재 시점로부터 이전 k 스텝의 시간 윈도우 데이터를 입력으로 받아 목적 시계열 데이터에 대한 향후 T 스텝의 분위 예측 값을 제공한다. 이때 분위 예측 값은 모델의 예측 값에 대한 불확실성 정도를 나타낸다. 예를 들어 25%와 75% 분위 예측 값은 50%의 불확실성 조건에서 모델 예측 값의 하한과 상한을 의미한다. 모델이 출력하는 예측 값의 확률이 높아지면 예측 값의 하한과 상한 범위는 좁아진다. 이러한 모델 예측 값의 확률 범위는 보다 종합적인 상태 판단을 위한 추가 정보가 된다.

제안 시스템은 실제 값과 예측 값의 차이를 절대 오차와 분위 오차의 2가지로 판단하되 절대 수치가 아닌 4개의 범주, G(Green), Y(Yellow), O(Orange), R(Red)로 판정한다. 절대 오차는 3개의 문턱값 th1, th2, th3 (th1<th2<th3)을 정의하고 50% 분위 예측값 pr50과 실제값 act의 차이와 각 문턱값을 비교하여 판정한다. 분위 오차는 2%, 10%, 25%, 50%, 75%, 90%, 98%의 7분위 예측값(각각 pr02, pr10, pr25, pr50, pr75, pr90, pr98)을 사용하여 실제값 act가 어느 분위 예측값 사이에 들어가는 지로 판정한다. 절대 오차와 분위 오차의 판정기준은 표 2와 같다.

Table 2.

Criteria for determining absolute and quantile errors

예측 대상의 상태는 절대 오차와 분위 오차를 모두 고려해야 한다. 분위 오차는 모델의 예측 확률을 고려한 실제값과 예측값의 차이(Unexpectedness)를 나타내므로 절대오차를 보정하는 역할을 할 수 있다. 이러한 고려에 따라 단일 시계열 데이터 기반 예측 대상 설비 상태의 백분율 지수를 표 3과 같이 설정하였다.

Table 3.

Equipment health index(percentage) based on a single data forecasting

모터 구동 설비의 진동 정보는 3축 가속도 센서 데이터를 모두 사용해 측정 및 예측이 이루어진다. 시계열 데이터 i 기반의 예측 대상 설비 상태 백분율 지수를 HIi라 할 때 n개의 시계열 데이터 1~n를 이용한 설비 상태 백분율 지수 HI는 식 (1)로 구한다. 식 (1)에서 wi는 시계열 데이터 i의 가중치이다.

$\[ HI=\frac{1}{n}\sum _{i=1}^n{w}_{i}H{I}_i \]$

(1)

Ⅳ. 구현 방법

4.1 모델 학습 및 추론 환경 구축

본 시스템의 분석 대상은 AC 모터로 구동하는 연마 설비로 연마를 위한 회전 동작이 설비의 진동을 유발한다. 학습 및 실시간 상태 분석을 위한 데이터는 연마 설비에 Bosch사의 XDK110 IoT 센서[28]를 부착하여 수집하였다. XDK110은 3축 가속도 센서를 포함한 여덟 종류의 센서와 함께 무선랜을 내장하고 있어, 측정된 데이터를 무선 전송한다. XDK110의 샘플링 속도는 명세상 센서 별로 182Hz에서 2000Hz 사이로 매우 빠른 편이지만 실제 운용환경에서는 센싱 데이터의 무선 전송까지의 처리 시간을 포함하여 초당 20회 내외의 데이터 송수신이 가능하였다. 본 시스템에서는 학습 및 예측을 위한 데이터로 12종의 센서 데이터와 10종의 설비 제어 PLC 데이터를 사용하였다. 시계열 DB로는 오픈소스인 InfluxDB[29]를 사용하였고 TFT 모델 학습은 PyTorch 및 PyTorch Forecasting 라이브러리를 이용하였다.

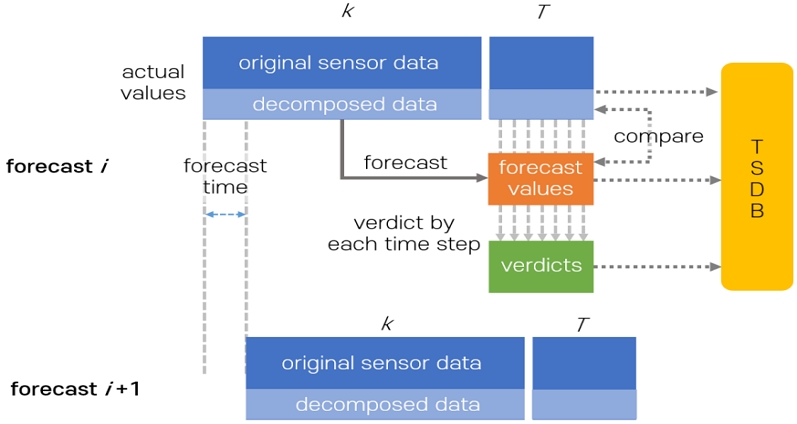
학습 데이터는 수신 데이터를 정제하여 약 180시간 분량의 데이터를 사용하였다. TFT 모델의 입출력 시간 단계 수 k와 T는 각각 300과 30으로 설정하였다. 학습 시에는 300 크기의 입력 윈도우를 1씩 이동시켜 학습을 수행하였으나 실시간 분석에는 신호의 분해와 모델 추론에 시간이 소요되므로 이전 예측을 끝낸 후 가장 최근의 300 단계 데이터를 가져와 다음 예측을 수행한다. 따라서 예측은 각 시간 단계마다 수행되지 않고 추론 시간에 따라 몇 단계씩 이동하며 수행된다. 예측에 소요되는 시간은 30 단계보다 작기 때문에 각 예측은 이전 예측과 일부 중첩된다. 시계열 DB에서 중첩되는 과거 예측은 신규 예측으로 업데이트된다. 그림 4는 모델이 예측을 수행하여 결과를 저장하는 방식을 보여준다.

Fig. 4.

Processing forecasts at each step

4.2 시각화 웹 플랫폼 구현

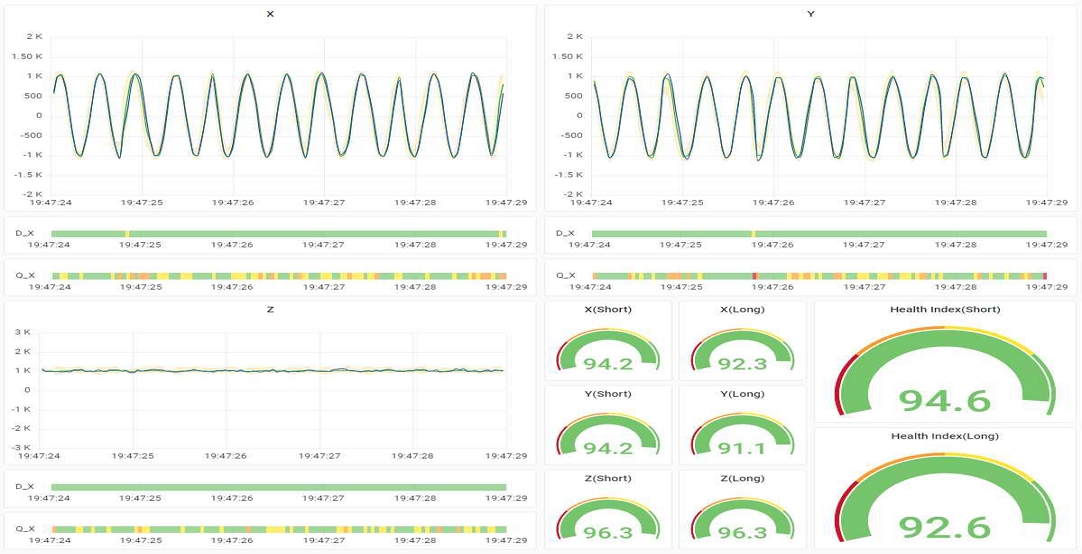
설비의 실시간 상태 모니터링을 위한 시각화 플랫폼으로 웹기반 오픈소스 시각화 애플리케이션인 Grafana를 사용하였다[30]. Grafana는 시계열 DB의 데이터를 실시간으로 가져와 다양한 형식으로 값을 표시할 수 있는 패널을 제공한다. 본 시스템에서 구현한 설비 상태 모니터링 화면 구성은 그림 5와 같다.

Fig. 5.

Equipment health monitoring screen

좌측 상/하단, 우측 상단에는 각각 X, Y, Z축 가속도 센서 데이터의 실제값과 예측값을 이용한 상태 정보가 표시된다. 우측 하단은 X, Y, Z축 가속도 센서 데이터를 기준으로 한 설비의 상태 지수(좌측 6개 게이지)와 3축 가속도 센서 데이터를 모두 고려한 설비의 상태 지수(우측 2개 게이지)를 보여준다. 설비의 상태지수(health index)는 현재 시점의 상태를 보여주는 ‘Short’와 최근의 상태를 보여주는 ‘Long’으로 구성되며 각각 5초 및 5분간의 시간 단계별 상태 지수의 평균값으로 표시된다.

3축 가속도 센서 데이터를 모두 고려한 설비의 상태 지수 계산 시 X, Y, Z축의 가중치 계수는 설비의 동작 특성을 고려해 각각 2, 2, 1로 부여하였다. 상태 지수는 상태 게이지와 함께 표시되며 게이지는 상태 지수 100~0의 구간을 4등분하여 순서대로 녹색, 노란색, 주황색, 빨간색의 색상으로 설비 상태를 표시한다.

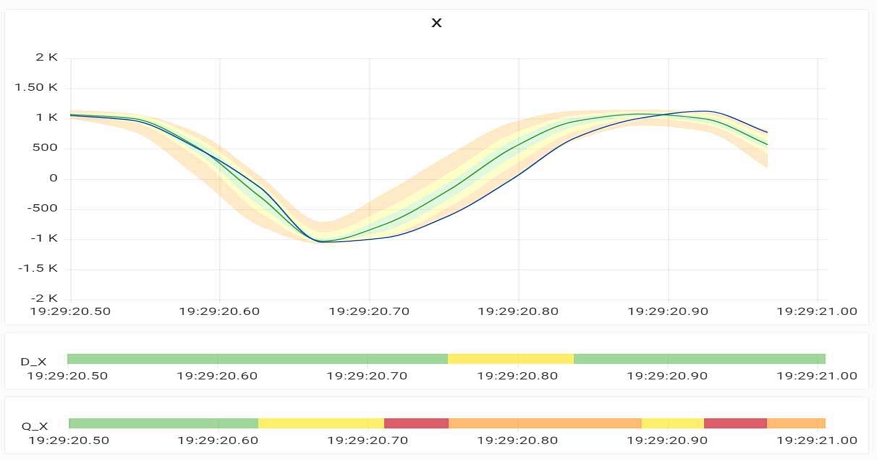
그림 6은 설비 그림 5의 좌측 상단에 위치한 X축 가속도 데이터 기반 상태 화면을 자세히 보여준다. 상단의 신호 그래프에는 실시간 실제값(청색 실선), 예측값(pr₅₀, 녹색 실선)과 함께 분위오차 판정범위가 색상(연녹색, 노란색, 주황색 영역)으로 표시된다. 하단의 두 막대는 각 시간 단계의 절대오차(D_X 표시)와 분위오차(Q_X 표시)의 판정을 색상으로 나타낸 것이다. 그림에서 볼 수 있듯이, 예측이 안정적으로 진행되고 있어 실제값과 예측값의 절대 오차는 크지 않다. 그러나 분위 오차의 경우, 판정 범주가 지속적으로 변하는 상황을 확인할 수 있다.

Fig. 6.

Health monitoring screen based on X-axis acceleration data

Ⅴ. 성능 평가

모터 구동 설비의 진동 정보를 분석하여 설비의 상태를 예측하는 모델의 성능을 평가하고, 최적의 학습 데이터를 찾아 성능을 극대화하기 위해 다음과 같이 평가 환경을 설정하였다. 먼저 다양한 종류의 학습 데이터에 대한 성능을 비교 평가하기 위해 각각 50만, 30만 시간 단계 데이터로 구성된 학습 및 시험 데이터를 준비하고 학습은 비교의 편의를 위해 25 에폭(Epoch)으로 제한하였다. 분석 대상 모델로는 TFT 모델과 함께 시계열 예측의 기본 모델이라 할 수 있는 1D-CNN+LSTM 모델을 사용하였다. 1D-CNN+LSTM 모델은 각각 2개씩의 1D-CNN, LSTM, Dense 네트워크가 일렬로 연결된 모델이다. TFT 모델은 다음 각 데이터를 이용해 학습하였다. 각 데이터의 학습 및 시험 데이터는 50만 개와 30만 개로 모두 동일하다.

• - X, Y, Z축 가속도 데이터
• - 가속도, PLC 데이터
• - 가속도, PLC, 가속도의 FFT3(STFT) 변환데이터
• - 가속도, PLC, 가속도의 FFT6(STFT) 변환데이터
• - 가속도, PLC, 가속도의 EMD3 변환데이터
• - 가속도, PLC, 가속도의 EMD6 변환데이터
• - 가속도, PLC, 가속도의 EEMD3 변환데이터
• - 가속도, PLC, 가속도의 VMD3 변환데이터
• - 가속도, PLC, 가속도의 VMD3,FFT3 변환데이터
• - 가속도, PLC, 가속도의 VMD3,FFT6 변환데이터

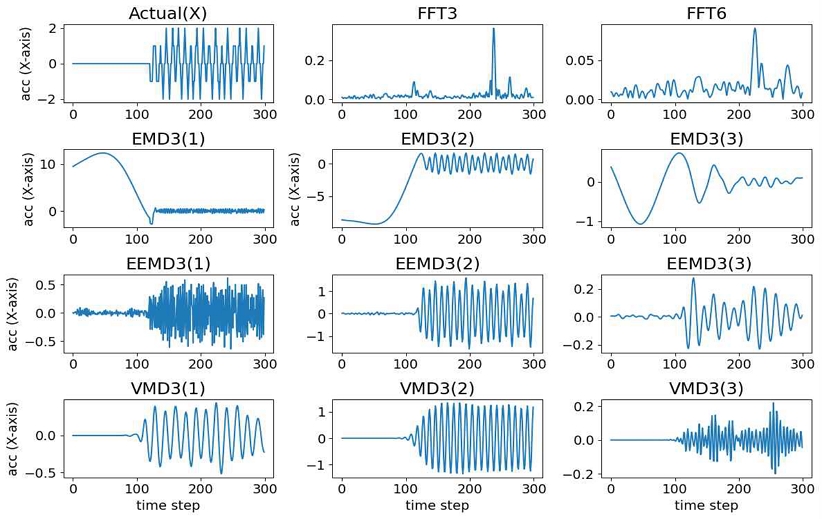
FFT3 및 FFT6 변환은 NumPy 라이브러리[31]의 fft 함수를 이용하여 가속도 데이터를 STFT 변환하였으며, 해상도를 각각 600, 1200으로 설정하여 오른쪽 300개의 샘플만 추출하는 방식을 사용하였다. EMD3, EMD6 및 EEMD3 변환은 PyEMD 라이브러리[32]에서 제공하는 EMD 및 EEMD 변환 함수를 사용하였으며 변환 신호는 각각 3개, 6개, 3개 사용하였다. VMD3 변환은 vmdpy 라이브러리[33]에서 제공하는 VMD 변환 함수로 3개의 변환 신호를 생성하도록 하였다. 그림 7은 정규화된 샘플 가속도 데이터(X축)에 대한 FFT3, FFT6, EMD3, EEMD3, VMD3 변환 신호를 각각 도시한 것이다.

Fig. 7.

Decomposed signals of sample acceleration data(X-axis)

평가 지표로서 오차 항목은 X,Y,Z축 가속도 데이터 각각에 대한 MAE(Mean Absolute Error), RMSE(Root Mean Square Error), SMAPE(Symmetric Mean Absolute Percentage Error)[34]와 전체 가속도 데이터에 대한 분위 오차(Quantile loss)[35]를 사용하였다. 비용 항목은 데이터 변환 시간 및 데이터 학습 시간을 사용하였다. 데이터 변환 시간은 FFT3 변환 시간을 1로 설정할 때의 상대 변환 시간을, 학습 시간은 가속도 데이터만 사용한 경우의 학습 시간을 1로 설정할 때의 상대 학습 시간을 사용하였다. 표 4는 각 학습 모델의 평가 결과를 보여준다.

Table 4.

Comparisons of forecasting performance when applying each decomposition technique

참조 모델인 1D-CNN+LSTM에 비해 TFT 모델은 RMSE 기준 30~40% 가량 우수한 예측 성능을 보였다.

TFT 모델의 경우 진동 데이터만으로 학습한 모델에 비해 PLC 데이터를 학습에 추가한 모델이 분위오차 기준 9.6% 정도 예측 성능이 향상되었는데, 이는 PLC 데이터의 효용성을 보여준다. 가속도 데이터를 분해한 신호를 추가하여 학습한 모델들의 예측 성능을 비교하였을 때, 분위오차 기준으로 FFT3 변환 데이터를 학습한 모델이 약 2.4%로 가장 높은 성능 향상을 보였다. 그다음으로 EMD6와 VMD3 변환 데이터를 추가하여 학습한 모델이 변환 데이터 없이 학습한 모델보다 약간의 성능 향상이 있었다. 그 외의 변환 데이터를 사용하여 학습한 경우 예측 성능이 오히려 하락하였고, 특히 VMD와 FFT 변환 데이터를 함께 사용하여 학습한 경우 하나의 변환 데이터를 사용하여 학습한 경우보다 오히려 성능이 저하되는 것을 확인할 수 있었다.

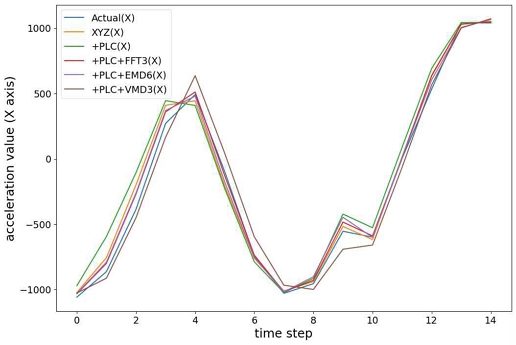
가속도 데이터의 분해 기법의 평가에서 신호 분해 시간도 실시간 데이터 처리를 위해 매우 중요하다. FFT의 경우 Intel i7 CPU가 장착된 컴퓨터에서샘플 당 1ms 이하의 빠른 속도로 신호 변환이 가능해서 변환 데이터의 추가 사용에 대한 부담이 거의 없었다. VMD, EMD, EEMD 변환의 경우에는 동일 컴퓨터에서 대략 샘플당 각각 0.09, 0.25, 0.47초가 소요되었다. 본 분석 대상 설비에서와 같이 초당 20회 내외의 예측을 수행하는 경우 이러한 변환들은 사용하기 어렵다. 제안하는 시스템은 평가 결과를 토대로 모델 학습 및 실시간 분석 데이터로 PLC 데이터와 가속도 센서 데이터의 FFT3 변환 데이터를 사용하였다. 그림 8은 15개 시간 포인트로 구성된 X축 샘플 가속도 데이터에 대한 주요 학습 모델들의 신호 예측 결과를 보여준다. 오른쪽 5개 포인트에서 확인할 수 있는 것처럼, 실제 신호(청색)가 일정한 패턴을 유지할 때 각 모델의 예측 신호는 거의 일치함을 볼 수 있다. 왼쪽 10개 포인트에서는 실제 신호의 불규칙한 변화를 확인할 수 있는데, 이러한 상황에서 각 모델의 예측 값 간에 차이가 발생한다. 이 샘플에서는 FFT3 및 VMD3 변환 데이터를 사용하여 학습한 모델이 실제 데이터와 가장 유사한 예측을 보여주었다.

Fig. 8.

Sample forecast acceleration signals from each trained model(X-axis)

Ⅵ. 결론 및 향후 과제

설비 예지 보전은 데이터를 실시간으로 분석하여 설비의 상태를 판단하고 필요한 조치를 사전에 수행함으로써 설비 운용의 효율성과 생산성을 높일 수 있는 스마트 공장의 핵심 기술이다. 설비 예지 보전 기술의 성능은 설비 상태를 정확히 예측할 수 있는 학습 모델과 이를 학습하기 위한 데이터에 크게 좌우된다. 본 논문은 제조 공장의 핵심 설비인 모터 구동 설비의 예지 보전을 위해 우수한 예측 성능을 가지는 TFT 모델과 진동 신호 분해 기반의 추가 학습 데이터를 사용하는 설비 상태 모니터링 및 이상 탐지 시스템을 제안하였다.

제안 시스템은 분석 설비에 부착된 IoT 센서로부터의 실시간 데이터를 수집하고, 시계열 DB, 실시간 예측 및 분석 알고리즘, 웹 기반 시각화 플랫폼을 활용하여 모터 구동 설비의 상세한 상태를 실시간으로 제공할 수 있었다. 특히 설비제어를 위한 PLC 데이터와 함께 진동 신호를 분해한 데이터를 TFT 모델 학습에 사용하여 예측 성능을 향상시켰다. 성능 평가 결과, 진동 신호를 FFT를 기반으로 STFT 변환하여 학습에 사용할 경우 최소 변환 시간 비용으로 약 2.4%의 성능 향상을 얻을 수 있었다.

제안 시스템의 설비 상태 분석 알고리즘에서 설비 상태 지수는 관리 경험에 따른 규칙 기반으로 설계되었으므로 절대적 수치가 아닌 백분율 기반의 상대적 수치를 보여준다. 제안 시스템을 다수의 설비에 구축하고 설비 관리 및 예지보전에 활용하여 운용 데이터가 충분히 축적될 경우 데이터 학습을 통해 보다 정확한 상태 지수를 제공하는 상태 분석 알고리즘 설계가 가능할 것이다. 장기 운용 데이터의 확보는 설비의 장기적 상태 변화를 파악하기 위해 매우 중요하며, 이를 기반으로 보다 장기적 예측을 수행할 수 있는 예측 모델 구현이 가능할 것이다.

Acknowledgments

이 연구는 금오공과대학교 학술연구비로 지원되었음(202001860001)

References

• J. H. Kim, D. C. Kim, S. H. Je, J. S. Lee, D. Kim, and S. H. Ji, "A Study on the Establishment of Prediction Conservation System for Smart Factory Facilities", Proc. of KIIT Conference, Jeju, Korea, pp. 703–706, Dec. 2022.
• G. E.P. Box and G. M. Jenkins, "Time Series Analysis: Forecasting and Control", Palgrave Macmillan Journals, Vol. 22, No. 2, pp. 199-201, Jun. 1971. [https://doi.org/10.2307/3008255]
• S. Hochreiter and J. Schmidhuber, "Long Short-Term Memory", Neural computation, Vol. 9, No. 8, pp. 1735-1780, Nov. 1997. [https://doi.org/10.1162/neco.1997.9.8.1735]
• T. Chen and C. Guestrin, "Xgboost: A Scalable Tree Boosting System", In Proc. of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 785-794, Aug. 2016. [https://doi.org/10.1145/2939672.2939785]
• G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye, and T. Y. Liu, "LightGBM: A Highly Efficient Gradient Boosting Decision Tree", Advances in Neural Information Processing Systems, pp. 3146-3154, Dec. 2017.
• B. Lim, S. O. Arik, N. Loeff, and T. Pfister, "Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting", arXiv:1912.09363, , Dec. 2019. [https://doi.org/10.48550/arXiv.1912.09363]
• A. Vaswani, et al., "Attention is all you need", Advances in neural information processing systems, pp. 5998-6008, Dec. 2017.
• M. K. Islam, D. Zhu, Y. Liu, A. Erkelens, N. Daniello, and J. Fox, "Interpreting County Level COVID-19 Infection and Feature Sensitivity using Deep Learning Time Series Models", arXiv:2210.03258, , Oct. 2022. [https://doi.org/10.48550/arXiv.2210.03258]
• F. M. Caldas and C. Soares, "A Temporal Fusion Transformer for Long-Term Explainable Prediction of Emergency Department Overcrowding", Machine Learning and Principles and Practice of Knowledge Discovery in Databases, pp. 71-88, 2022. [https://doi.org/10.1007/978-3-031-23618-1_5]
• L. Wang, A. Tien, and J. Chou, "Multi-Airport Delay Prediction with Transformers", AIAA AVIATION 2022 Forum, Jun. 2022. [https://doi.org/10.2514/6.2022-3707]
• D. S. Civitarese, D. Szwarcman, B. Zadrozny, and C. Watson, "Extreme Precipitation Seasonal Forecast Using a Transformer Neural Network", ICML, arXiv: 2107.06846, , Jul. 2021. [https://doi.org/10.48550/arXiv.2107.06846]
• M. Jiang, X. Jiang, and Q. Zhou, "Temporal fusion transformer using variational mode decomposition for wind power forecasting", arXiv:2302.01222, , Feb. 2023. [https://doi.org/10.48550/arXiv.2302.01222]
• X. Jiang, M. Jiang, and Q. Zhou, "Day-Ahead PV Power Forecasting Based on MSTL-TFT", arXiv:2301.05911, , Jan. 2023. [https://doi.org/10.48550/arXiv.2301.05911]
• C. Li, Z. Qiu, Y. Ma, and M. Li, "A Long-term Dependent and Trustworthy Approach to Reactor Accident Prognosis based on Temporal Fusion Transformer", arXiv:2210.17298, , Oct. 2022. [https://doi.org/10.48550/arXiv.2210.17298]
• D. H. Ballard, "Modular learning in neural networks", Proc. of the sixth National conference on Artificial intelligence, Vol. 1, pp. 279-284, Jul. 1987.
• M. J. Oh, E. S. Choi, K. W. R, J. S. Kim, and W. Cho, "A Study on the Design of Supervised and Unsupervised Learning Models for Fault and Anomaly Detection in Manufacturing Facilities", The Korea Journal of BigData, Vol. 6, No. 1, pp. 23-35, Jun. 2021. [https://doi.org/10.36498/kbigdt.2021.6.1.23]
• Jaehong Seo, Junsung Park, Joon Woo Yoo, Heejun Park, "Anomaly Detection System in Mechanical Facility Equipment: Using Long Short-Term Memory Variational Autoencoder", Journal of KSQM, Vol. 49, No. 4, pp. 581-594, Dec. 2021. [https://doi.org/10.7469/JKSQM.2021.49.4.581]
• C. Qu, Z. Zhou, Z. Liu, and S. Jia, "Predictive anomaly detection for marine diesel engine based on echo state network and autoencoder", Energy Reports, Vol. 8, No. 5, pp. 998-1003, Jul. 2022. [https://doi.org/10.1016/j.egyr.2022.01.225]
• U. D. Schiller and J. J. Steil, "Analyzing the weight dynamics of recurrent learning algorithms", Neurocomputing, Vol. 63, pp. 5-23, Jan. 2005. [https://doi.org/10.1016/j.neucom.2004.04.006]
• S. Givnan, C. Chalmers, P. Fergus, S. Ortega-Martorell, and T. Whalley, "Anomaly Detection Using Autoencoder Reconstruction upon Industrial Motors", Sensors, Vol. 22, No. 9, Apr. 2022. [https://doi.org/10.3390/s22093166]
• E. Sejdić, I. Djurović, and J. Jiang, "Time-frequency feature representation using energy concentration: An overview of recent advances", Digital Signal Proc., Vol. 19, No. 1, pp. 153-183, Jan. 2009. [https://doi.org/10.1016/j.dsp.2007.12.004]
• N. E. Huang, et al., "The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis", Proc. Mathematical, Physical and Engineering Sciences, Vol. 454, No. 1971, Mar. 1998. [https://doi.org/10.1098/rspa.1998.0193]
• Z. Wu and N. E. Huang, "Ensemble empirical mode decomposition: a noise-assisted data analysis method", Advances in adaptive data analysis, Vol. 1, No. 1, pp. 1-41, 2009. [https://doi.org/10.1142/S1793536909000047]
• M. T. Heideman, D. H. Johnson, and C. S. Burrus, "Gauss and the history of the fast Fourier transform", Archive for History of Exact Sciences, Vol. 34, No. 3, pp. 265-277, 1985. [https://doi.org/10.1007/BF00348431]
• K. Dragomiretskiy and D. Zosso, "Variational Mode Decomposition", IEEE Transactions on Signal Proc., Vol. 62, No. 3, pp. 531-544, Feb. 2014. [https://doi.org/10.1109/TSP.2013.2288675]
• K. Bandara, R. J. Hyndman, and C. Bergmeir, "MSTL: A Seasonal-Trend Decomposition Algorithm for Time Series with Multiple Seasonal Patterns", arXiv:2107.13462, , Jul. 2021. [https://doi.org/10.1504/IJOR.2022.10048281]
• L. Sasal, T. Chakraborty, and A. Hadid, "W-Transformers : A Wavelet-based Transformer Framework for Univariate Time Series Forecasting", arXiv:2209.03945, , Sep. 2022. [https://doi.org/10.1109/ICMLA55696.2022.00111]
• LEGIC, "XDK", https://www.xdk.io/, [accessed: Apr. 25, 2023]
• InfluxData, "InfluxDB", https://www.influxdata.com/time-series-platform/influxdb/, [accessed: Apr. 25, 2023]
• Grafana Labs, "Grafana" https://grafana.com/, [accessed: Apr. 25, 2023]
• NumPy, "The fundamental package for scientific computing with Python", https://numpy.org/, [accessed: Apr. 25, 2023]
• PyEMD, "Python implementation of Empirical Mode Decomposition (EMD) and its variations", https://pyemd.readthedocs.io/, [accessed: Apr. 25, 2023]
• Vinícius Carvalho, "vmdpy: Variational mode decomposition in Python", https://github.com/vrcarva/vmdpy, [accessed: Apr. 25, 2023]
• Wikipedia, "Symmetric mean absolute percentage error", https://en.wikipedia.org/wiki/Symmetric_mean_absolute_percentage_error, [accessed: Apr. 25, 2023]
• Wikipedia, https://en.wikipedia.org/wiki/Quantile_regression, [accessed: Apr. 25, 2023]