[ Article ]

The Journal of Korean Institute of Information Technology - Vol. 18, No. 2, pp.101-109

ISSN: 1598-8619 (Print) 2093-7571 (Online)

Print publication date 28 Feb 2020

Received 28 Oct 2019 Revised 13 Nov 2019 Accepted 16 Nov 2019

DOI: https://doi.org/10.14801/jkiit.2020.18.2.101

레이더 측정과 확장 칼만필터를 이용한 발사체 착점 추정

강봉수^*

; 이인수^**

*한화시스템(주) 전문연구원
**경북대학교 IT대학 전자공학부 교수(교신저자)

Estimation of a Projectile Impact Point Using Radar Measurement and Extended Kalman Filter

Bong-Soo Kang^*

; In-Soo Lee^**

Correspondence to: In-Soo Lee School of Electronics Engineering, Kyungpook National University, 80 Daehakro, Bukgu, Daegu, 702-701, Korea Tel.: +82-53-950-7843, Email: insoolee@knu.ac.kr

초록

함포를 이용하여 발사체를 발사하는 경우 자함에 탑재된 환경 센서가 측정하지 못하는 외탄도적 환경 정보 미확보에 따라 표적과 발사체의 착점은 오차를 가지게 된다. 이때 표적을 명중시키기 위해서는 발생한 오차를 보정해야 하므로 발사체의 착점을 정확히 추정하는 것이 필요하다. 이를 위해 발사체 운동방정식은 NATO 표준 문서 STANAG 4355에 표준화되어 있는 항력, 중력, 코리올리힘이 반영된 PMM(Point Mass Trajectory Model)을 사용하였고, 비선형의 발사체 운동에 대한 레이더 측정정보 처리에는 1차 확장 칼만필터 기반의 기법을 적용하였다. 필터의 공정잡음 표준편차 결정과 예측시간에 따른 성능 확인을 위해서는 Monte Carlo Simulation을 수행하였으며, 예측 성능 분석을 통해서는 발사체 운동모델에 반영된 코리올리힘보다는 풍향, 풍속에 의한 항력이 발사체의 착점 예측 오차를 크게 발생시킨다는 것을 알 수 있었다. 발사체 발사 고각을 달리한 실험을 통해서는 발사체의 착점 RMS 오차가 발사체의 비행거리에 비례함도 확인할 수 있었다.

Abstract

In this thesis, we propose a projectile impact point estimation method based on the first-order extended Kalman filter using radar measurement information. The equation of motion was used to reflect drag, gravity, and Coriolis forces, standardized in the NATO standard document STANAG 4355. For nonlinear tracking, such as projectile motion models, linearization must be performed in deriving the filtering equation. In this case, real-time linear Taylor approximation is performed from previous estimated state variables, and the Kalman filter obtained here is called a first-order extended Kalman filter. Based on this, we designed a first-order extended Kalman filter based on projectile motion model. Monte Carlo Simulation was performed to determine the parameters of the filter and to verify the performance according to the prediction time. It has been confirmed that drag caused by wind direction and wind speed causes a large error in predicting the impact point of the projectile. And It was also confirmed that the RMS error is proportional to the projectile's flight distance.

Keywords:

estimation, impact point, projectile, extended kalman filter, radar measurement

Ⅰ. 서 론

현대 해상전에 있어 과학기술의 발달과 함께 새로운 공격 및 방어 개념이 지속적으로 도출되고 있으며, 축소되었던 함포의 필요성은 21세기를 거치며 새롭게 조명받고 있다. 함포의 크기에 대한 경쟁 시기였던 2차 대전을 기점으로 함포의 전성시대는 유도무기의 발달과 함께 내리막길을 걸어왔으나, 21세기를 거치며 발달된 IT 기술에 힘입어 저비용 고효율로 무장된 함포의 중요성이 대두되었다[1]. 이런 함포를 이용하여 발사체를 발사하는 경우 자함에 탑재된 환경 센서가 측정하지 못하는 외탄도적 환경 정보 미확보에 따라 표적과 발사체의 착점을 오차를 가지게 되며, 이런 오차를 보정하여 표적을 명중시키기 위해서는 발사체의 착점을 정확히 추정하는 것이 필요하다[1].

대규모 살상력을 가지는 탄도탄(Ballistic missile)의 경우 조기경보와 격추를 위한 방어체계 구축이 목적이며, 발사체에 대한 정보를 모르므로 기본적인 운동모델에 의한 비행궤적과 착점 추정의 연구가 이루어졌다[2][3]. 그리고 기존 포탄에 추가적인 Kit를 부착하는 형태인 탄도수정탄(Course correction munition)의 경우 발사체에 장착된 센서의 측정정보를 이용하며, 착점에 대한 예측보다는 보정 방식을 통한 목표지점으로의 유도가 더 큰 목적으로 연구되어왔다[4]-[6].

자함의 함포에서 발사된 발사체는 정보를 알고 있으며, 비행하는 동안의 위치 정보는 자함의 레이더 측정을 통해서 획득할 수 있다. 그러나 측정된 위치 정보에는 잡음이 포함되어 있으며, 지형이나 표적에 의해 레이더가 발사체의 최종 착점까지 측정되지 않을 수도 있다. 이를 해결하기 위해서는 추적필터가 필요하며, 가장 널리 알려진 추적필터는 칼만필터다. 칼만필터링 절차는 선형모델에서 상태변수들을 추정하기 위해 만들어진 것이므로 발사체 운동모델과 같은 비선형 추적을 위해서 필터링 식을 유도하는 과정에서 선형화가 이루어져야 한다[7]. 이때 이전의 추정된 상태변수로부터 실시간 선형 테일러 근사화를 하게 되고, 여기서 얻어지는 칼만필터를 1차 확장 칼만필터라 한다[8].

본 논문에서는 레이더 측정정보를 이용한 1차 확장 칼만필터 기반의 발사체 착점 추정 방법을 제시하였다. 착점 추정을 위한 발사체의 정보는 155mm HE M107에 대한 정보를 사용하였고[9], 운동방정식은 NATO 표준문서 STANAG 4355[10]에 표준화된 항력, 중력, 코리올리힘을 반영하는 식을 사용하였다.

그리고 이를 바탕으로 발사체 운동모델 기반의 1차 확장 칼만필터를 설계하였다. 필터의 파라미터 결정과 예측시간에 따른 성능을 확인하기 위하여는 몬테카를로 시뮬레이션(Monte Carlo simulation)을 수행하였고, 발사체의 착점 예측 오차를 발생시키는 요인의 분석을 위한 실험도 수행하였다.

본 논문의 구성은 다음과 같다. 2장에서는 발사체 운동모델에 대해 기술하고, 3장에서는 발사체의 착점을 예측하기 위한 필터로 발사체 운동모델 기반 1차 확장 칼만필터를 설명한다. 4장에서는 발사체 착점 예측 성능에 대한 실험과 결과를 분석하고, 마지막으로 5장에서 결론을 맺는다.

Ⅱ. 발사체 운동모델

항공기나 함정은 운용자의 조종에 따라 등속, 등가속, 회전 등의 다양한 운동을 하며, 몇 단의 추진을 가지는 로켓은 단에 따라 다른 기동을 한다. 이와는 달리 발사 후에 추가적인 추진력이 작용하지 않는 발사체의 경우는 NATO 표준문서 STANAG 4355에 표준화되어 있는 운동방정식과 같은 운동을 하게 된다[10][11].

2.1 발사체 운동 좌표계

운동모델 적용 좌표계는 XYZ 좌표계를 사용한다. XYZ 좌표계는 좌표계 원점을 기준으로 선형 X, Y 및 Z 좌표를 사용하는 평면형 시스템으로 발사체를 발사한 지점이 좌표계의 원점이다.

발사체의 운동모델은 XYZ 좌표계에서 정의하며, 3장의 발사체 운동모델 기반 확장 칼만필터에서 상태변수도 XYZ 좌표계 값을 사용한다.

2.2 레이더 측정 좌표계

3차원 레이더의 표적 측정 정보는 표적거리 r, 방위각 θ, 고각 ϕ으로 주어지며, 아래의 식과 같은 레이더 측정식을 가진다.

r k θ k ϕ k = x 2 k + y 2 k + z 2 k arctan 2 x k, y k arcsin z x 2 k + y 2 k + z 2 k + ω k

(1)

이때 ω(k)는 측정잡음으로 평균이 0이고, 공분산은 다음과 같이 R(k)로 주어지는 백색 가우시안 잡음으로 가정한다. 이때 $σ r 2$ 는 표적거리 측정잡음의 분산, $σ θ 2$ 는 방위각 측정잡음의 분산, 그리고 $σ ϕ 2$ 는 고각 측정잡음의 분산을 의미하며, 잡음들은 서로 상관이 없는 것으로 가정한다[12].

R k = σ r 2 00 0 σ θ 2 0 00 σ ϕ 2

(2)

2.3 발사체 운동모델

NATO 표준문서 STANAG 4355에 표준화되어 있는 운동모델 중 PMM(Point Mass trajectory Model)은 발사체에 작용하는 기본 힘으로 중력(Gravity force, $G F →$ ), 항력(Drag force, $D F →$ ), 코리올리힘(Coriolis force, $C F →$ )이 고려되었으며, 질량 m, 가속도 $a →$ 의 발사체에 대해서 다음 형식의 운동방정식으로 정의하였다[10].

F = m a → = G F → + D F → + C F →

(3)

발사체는 참고문헌[9]의 155mm HE M107 정보를 사용함에 따라 발사체의 직경은 0.155m, 발사체 발사속력은 562.0m/s이며, 발사체의 질량은 41.86kg 값을 적용하였다. 대기조건은 국제표준대기인 기압 1013.25hPa, 기온 15°C를 적용하였다.

2.3.1 중력

중력 $G F →$ 은 발사체의 질량 m과 중력가속도 $g →$ 의 곱으로 식 (4)와 같다. 중력가속도의 경우 북위 37°의 중력가속도 9.799621m/s²을 적용하였다.

중력가속도는 지구 중심과의 거리인 고도 x_z에 의한 영향을 받으며, 고도 1km마다 3.086×10^-3m/s² 감소한다. 수 km를 상승하는 발사체는 이러한 영향을 받으므로 이를 운동방정식에 반영하였다[13].

G F → = m g →

(4)

2.3.2 항력

발사체의 운동에 영향을 미치는 기본적인 힘으로 물체가 유체 속을 일정한 상대 속도를 갖고 운동할 때 물체의 진행 방향에 대해 작용하는 힘을 항력 $D F →$ 이라고 하며 식 (5)와 같이 정의되어 있다.

D F → = - π ρ i d 2 8 C D v v →

(5)

여기서 π : 원주율 ( = 3.1415926 )
　　　 ρ : 공기 밀도 ( kg·m^-3 )
　　　 i : Form factor ( = 1 )
　　　 d : 발사체 직경 ( = 0.155m )
　　　 C_D : 항력계수
　　　 $v →$ : 공기 중에 대한 상대 속도 벡터
　　　　 ( $v → = u → - w →$ )
　　　 $w →$ : 공기의 속도 벡터
　　　 $u →$ : 발사체의 속도 벡터

발사체의 운동에서 바람은 없다고 가정한다. 항력계수는 발사체의 크기, 모양에 따라 달라지며, 본 연구에서는 참고문헌[14]에 있는 155mm HE M107 발사체와 유사한 형상의 항력계수 값을 보간법으로 적용하였다. 항력계수 C_D는 발사체의 속력을 음속으로 나눈 마하수 M에 의해 결정되며, 마하수 M에 대한 함수로 식 (6)과 같이 표현할 수 있다.

C D = D r a g M

(6)

2.3.3 코리올리힘

코리올리힘은 회전하는 계에서 운동하는 물체에 작용하는 관성력으로 식 (7)과 같다. 보통 지구의 자전에 의한 효과를 고려할 때 쓰이며, 먼 거리를 직선운동하는 물체의 경우 북반구에서는 오른쪽으로 휘어지며 움직이는 것처럼 보인다. 지구 자전축에 대한 좌표계의 각속도 벡터는 중력과 마찬가지로 북위 37°의 각속도를 사용하였다.

C F → = - 2 m ω → × u →

(7)

여기서 m : 발사체 질량 ( = 41.86kg )
　　　 $ω →$ : 지구 자전축의 좌표계 각속도 벡터
　　　 $u →$ : 발사체의 속도 벡터

Ⅲ. 발사체 운동모델 기반 확장 칼만필터 설계

발사체 운동 좌표계의 초기 위치에서 특정 방위각, 고각으로 발사된 발사체는 위에서 기술한 중력, 항력, 코리올리힘이 작용하는 발사체 운동방정식에 의해 가속도 운동을 한다. 이때 이산 시간 상태 벡터는 아래와 같이 정의한다.

x k = x x k, x x ˙ k, x y k, x y ˙ k, x z k, x z ˙ k T

(8)

이때 k는 균일한 간격 T를 갖는 t = kT에 대응하는 이산 시간 인덱스를 나타낸다. 미분 형태의 방정식은 속도는 단위 시간당 위치의 변화량, 가속도는 단위 시간당 속도의 변화량으로 이를 이산 시간 형태로 나타내면 X축은 아래와 같으며, Y축과 Z축도 동일한 형태를 가진다. 이때 a_x (…)는 운동방정식으로 계산한 현재의 X축 가속도이다.

x x k + 1 = x x k + T x x ˙ k + T 2 2 a x x x ˙ k, x y ˙ k, x z ˙ k, x z k

(9)

x x ˙ k + 1 = x x ˙ k + T a x x x ˙ k, x y ˙ k, x z ˙ k, x z k

(10)

x(k)은 현재의 고도 x_z(k)와 속도 $x ˙ k$ 를 기반으로 전개되며, 식 (8)과 같이 정의된 이산 시간 상태 벡터에 의해 식 (11)과 같은 이산 시간 상태 방정식을 나타낼 수 있다.

x k + 1 = f k, x k

(11)

식 (11)에서 발사체 운동방정식의 불확정성을 모델링하는 공정잡음 벡터 Γv(k)를 도입하면 아래와 같이 나타낼 수 있다.

x k + 1 = f k, x k + Γ v k

(12)

v(k)는 zero-mean white sequence이고, Γ는 noise gain으로 벡터로 잡음의 공분산 행렬은 아래 식과 같이 구해진다.

Q k = E Γ v k v k Γ' = Γ σ v 2 Γ' = 14 T 4 12 T 3 0000 12 T 3 T 2 0000 00 14 T 4 12 T 3 00 00 12 T 3 T 2 00 0000 14 T 4 12 T 3 0000 12 T 3 T 2 σ v 2

(13)

여기서 파라미터 $σ v 2$ 은 잡음의 분산이며, 샘플링 간격 T에 대한 $x x ˙ k, x y ˙ k, x z ˙ k$ 의 속도 변화의 강도를 특징한다. 또한 백색 잡음 시퀀스의 합이기 때문에 이산 시간 Wiener 프로세스가 된다. 이 공정잡음 벡터 Γv(k)는 평균 위치의 시간 변화를 수용하고, 속도와 가속도가 점차적으로 진화하도록 허용한다.

이산 시간 관측 모델 식은 다음과 같다.

z k = h k, x k + w k

(14)

여기서 z(k)는 시간 k에서의 측정값, 측정잡음 w(k)는 분산 R(k)를 갖는 제로 평균 백색 잡음의 시퀀스로써 앞의 레이더 측정 좌표계에서 설명하였다. 시간 k까지의 측정 세트는 Z^k = z(1), z(2), …, z(k)로 표시된다. 목표는 측정 세트 Z^k에 따라 시간 kT + τ(τ > 0)에서의 위치를 예측하는 것이다.

식 (14)와 같이 주어지는 비선형 시스템의 상태벡터를 계산적으로 정확히 추정하기가 어려운 경우 확장 칼만필터를 이용하여 간단히 계산할 수 있다.

먼저, 초기상태 x(0)의 추정치 $x^00$ 과 공분산행렬 P(0∣0)이 주어지고, 공정잡음 v와 측정잡음 w는 x(0)에 대해 독립적이라고 가정한다. 엄격히 말해서 P(k∣k)는 공분산행렬이 아니고, $x k - x^k k$ 의 평균제곱오차행렬로서 k시간까지의 측정의 집합을 표현하기 위하여 다음과 같이 표현할 수 있다. 목표는 측정 세트 Z^k에 따라 시간 kT + τ(τ > 0)에서의 위치를 예측하는 것이다.

Z k ≜ z j, j = 1, …, k

(15)

예측 상태벡터 $x^k + 1 k$ 은 식 (12)의 비선형식을 $x^k k$ 에 대해서 1차 Taylor 급수로 전개하여 평균을 취함으로써 1차 확장 칼만필터가 된다. 아래에 예측 상태벡터와 오차공분산행렬을 나타내었다.

x^k + 1 k = f k, x^k k

(16)

P k + 1 k = f x k P k k f x k' + Q k

(17)

그리고 벡터 f의 Jacobian f_x(k)는 다음과 같다.

f x k ≜ ∇ x f k, x'' x = x^k k ≜ ∂ f ∂ x

(18)

마찬가지 방법으로 측정의 예측과 공분산 행렬은 다음 식에 의해 주어진다.

z^k + 1 k = h k + 1, x^k + 1 k

(19)

S k + 1 = h x k + 1 P k + 1 k h x k + 1' + R k + 1

(20)

여기서 h_x (k + 1)는 $x^k + 1 k$ 에서 계산된 벡터 h의 Jacobian으로 다음과 같다.

h x k + 1 ≜ ∇ x h k + 1, x'' x = x^k + 1 k ≜ ∂ h ∂ x

(21)

새로운 측정치 z(k + 1)과 상응하는 공분산은 다음과 같다.

x^k + 1 k + 1 = x^k + 1 k + W k + 1 z k + 1 - z^k + 1 k

(22)

P k + 1 k + 1 = P k + 1 k - W k + 1 S k + 1 W k + 1'

(23)

필터이득 W(k + 1)는 다음과 같이 얻어진다.

W k + 1 = P k + 1 k H k + 1' S k + 1 - 1

(24)

이 결과는 다시 식 (16), (17)의 입력으로 사용되어 확장 칼만필터의 순환식이 구성된다.

초기상태 값의 설정을 위해 칼만필터는 레이더 측정된 세 번째 데이터부터 수행하며, 앞선 2개의 데이터를 이용하여 초기상태 값을 설정한다.

상태 벡터 x(0)의 추정치인 $x^00$ 의 초기치 위치는 두 번째 측정데이터, 속도는 두 측정데이터의 변화량으로 설정하였고, 초기 공분산 오차 P(0∣0)는 다음과 같다.

P 00 = σ x 2 σ x 2 T 0000 σ x 2 T 2 σ x 2 T 2 0000 00 σ y 2 σ y 2 T 00 00 σ y 2 T 2 σ y 2 T 2 00 0000 σ z 2 σ z 2 T 0000 σ z 2 T 2 σ z 2 T 2

(25)

공분산 오차에서 $σ x 2, σ y 2, σ z 2$ 는 레이더 측정 좌표계의 측정치 z(-1)를 직교좌표계로 변환하고, 분산 $σ r 2, σ θ 2, σ ϕ 2$ 를 적용하여 계산한 값이다.

Ⅳ. 성능실험 및 분석

4.1 레이더 측정 데이터 생성

발사체 운동모델 기반 1차 확장 칼만필터에 대한 분석은 발사체 최종 착점의 예측에 주목하며, 발사체 측정 정보는 실제 레이더로부터 들어온 데이터가 아닌 발사체 운동방정식을 1msec 간격의 4차 룬지-쿠타법(Runge-Kutta)[15]으로 적분하여 생성하였다. 그리고 식 (2)와 같은 공분산 행렬을 갖는 백색 가우시안을 측정 오차로 발생시켜 실험을 위한 발사체의 레이더 측정 데이터를 생성하였다.

4.2 발사체 운동모델 기반 1차 확장 칼만필터 파라미터 설계

레이더 측정 주기는 0.1sec로 가정하며, 이에 따라 발사체 운동모델 기반 1차 확장 칼만필터의 업데이트 주기 T는 0.1sec이다. 레이더 측정오차는 백색 가우시안 잡음으로 평균이 0이며 표준편차는 각각 σ_r = 5m, σ_θ = 0.5mrad, σ_ϕ = 0.5mrad으로 가정하였다.

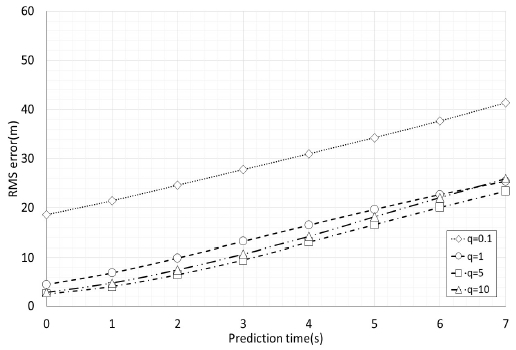
공정잡음 표준편차 q 값을 결정하기 위해서 발사체 발사 방위각 0°, 고각 35°, 풍향 0°, 풍속은 15m/s로 고정값이며, 결정을 위한 q 값과 예측시간의 길이를 달리하여 실험을 진행하였다. 발사체 착점 RMS 오차의 경우 측정오차를 갖는 레이더 측정데이터에 대한 분석을 위해서 몬테 카를로 시뮬레이션을 10,000번 실행하였다.

Fig 1.

Projectile impact point RMS error to determine q value

예측시간의 길이가 0초인 경우 q 값이 0.1일 때를 제외하면 모두 착점 RMS 오차가 5m 이내로 양호하였다. 반면 예측시간의 길이가 길어짐에 따라 RMS 오차값은 모든 q 값에서 증가하였다. 예측시간의 길이가 같은 경우에 q 값 1, 5, 10에 대한 RMS 오차값은 4m 이내의 차이를 보였다. 그리고 q 값이 0.1인 경우는 다른 q 값에 대한 RMS 오차값보다 약 14m 이상 큰 결과를 보였다. 이에 따라 적정한 q 값 결정에서 0.1은 제외하며, 나머지 q 값 1, 5, 10중에 적정한 q 값은 4.3절의 예측 성능 분석을 통해서 결정할 수 있다.

4.3 예측성능 분석

예측 성능 분석을 위해서는 발사체의 착점에 대한 RMS 오차를 분석하였다. 그리고 발사체의 착점을 예측하기 위해 레이더의 마지막 측정에 대한 필터의 추정값으로부터 업데이트 주기 T는 1msec로 하여 발사체 운동방정식으로 계산한 값을 필터의 측정치로 입력해 착점까지 예측하였다.

4.3.1 코리올리힘 영향성 분석

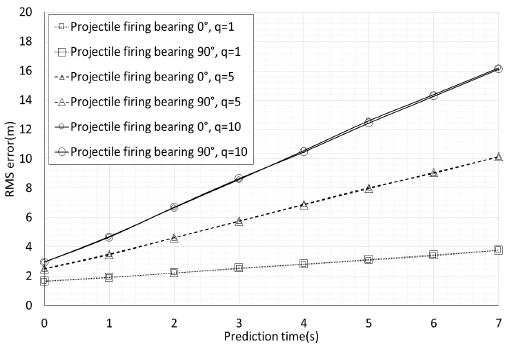
코리올리힘은 지구 자전에 의한 효과로 영향성 분석을 위해 발사체 발사 고각은 35°, 풍속은 0m/s이며, 발사 방위각은 지구 자전 방향인 90°와 수직 방향인 0°의 조건에서 시뮬레이션을 수행하였다. 다음의 그림 2는 발사체 발사 방위각에 따른 실험 결과를 제시한다.

Fig 2.

RMS error for projectile firing bearing

예측시간의 길이가 길어짐에 따라 RMS 오차값은 증가하며, 예측시간 길이 1초까지는 RMS 오차가 5m 내에 들어올 정도로 양호하다. q 값에 따라서 결과는 다르나 같은 q 값에 대해 발사체 발사 방위각 0°와 90°는 0.2m 이내의 차이를 보일 정도로 비슷한 결과가 나왔다. 이것으로 보아 코리올리힘은 예측 오차를 크게 발생시키지 않는다고 할 수 있다. 그리고 q 값은 1일 때 가장 결과가 좋았으며, 다음 실험을 통해서 계속 분석하였다.

4.3.2 풍향, 풍속에 의한 항력의 영향성 분석

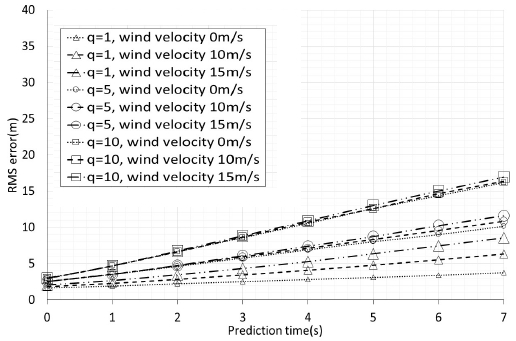
발사체에 작용하는 항력은 풍향과 풍속에 따라서 힘의 크기가 다르게 작용하므로 영향성 분석 실험에서 발사체 발사 고각은 바람의 영향을 많이 받도록 35°로 시뮬레이션을 수행하였다. 다음은 풍향에 따른 실험 결과를 제시한다.

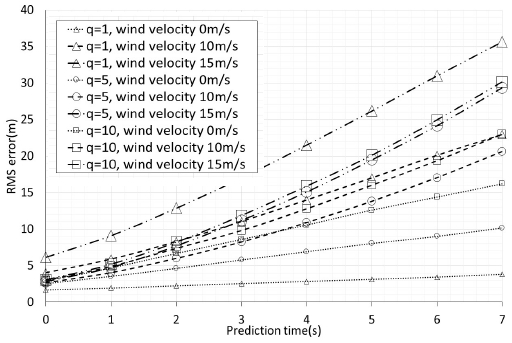
모든 결과에서 q 값이 같은 경우 풍속이 증가함에 따라 RMS 오차값도 증가하였다. 특히 풍향 180°, q 값 1, 예측시간 길이 7초일 때 RMS 오차값은 풍속 0m/s일 때 보다 15m/s일 때 30m 이상 커지는 것을 확인할 수 있다. 이는 예측이 시작되면 발사체 운동모델을 이용하여 예측하게 되는데, 풍향, 풍속이 반영되지 않기 때문으로 추정된다.

발사체 비행방향에 대해 바람이 측면으로 부는 풍향 90°인 경우 RMS 오차값이 발사체 비행방향인 풍향 180°의 결과보다 최대 약 27m 작았다. 이는 바람이 측면으로 부는 경우 비행방향에 대한 발사체의 속도에 비하면 수직으로 작용하는 풍속은 작아 전체적인 발사체 비행궤적 변화에 영향이 적은 것이라 추정된다. 발사체 발사 방위별 결과가 거의 비슷했던 그림 2와 비교하면 풍속에 따라 최대 30m 이상 차이가 발생하므로 풍향, 풍속에 의한 항력은 코리올리힘보다 예측 오차를 크게 발생시킨다고 할 수 있다.

그림 3의 풍향 90°인 경우 결과를 보면 q 값 1이 가장 좋고, 5와 10 순서인 것을 확인할 수 있다. 그러나 그림 4의 풍향 180°일 때, 풍속이 0m/s에서 15m/s로 증가함에 따른 예측시간의 길이 7초일 때 RMS 오차 변화가 q=1일 때 약 32m, q=5일 때 약 19m, q=10일 때 약 14m로 q 값이 1일 때 가장 크다. 즉, q 값 1은 풍속 0m/s의 이상적인 경우는 예측 오차를 작게 발생시키나 풍향, 풍속의 변화가 생기면 예측 오차를 크게 발생시키는 것이다. 일반적으로 이산 시간 프로세스에서 공정잡음의 표준편차 σ_v는 최대가속도 크기 a_M에 대해 다음과 같이 구해진다[16].

Fig. 3.

RMS error for 90 degree wind direction

Fig. 4.

RMS error for 180 degree wind direction

0.5 a M ≤ σ v ≤ a M

(26)

발사체 운동모델에서 해수면의 중력가속도는 약 9.8m/s²이고, 발사체 고도, 항력과 코리올리힘에 의해 가속도는 변하게 된다. 최대가속도 값은 여러 요인에 따라 달라질 수 있으나 중력가속도 값보다 큰 것은 분명하다. 이에 비해 q 값 1은 작으므로 풍속의 변화에 대한 예측에서 오차를 보인 것으로 추정된다. 이에 따라 적정한 q 값에서 1은 제외하며, 모든 시나리오에서 q 값 5는 10일 때 보다 결과가 좋았으므로 적정한 공정잡음 표준편차 q는 5로 결정하였다. 따라서 앞으로의 실험에서 q 값은 5로 시뮬레이션을 수행하였다.

4.3.3 발사체 비행거리의 영향성 분석

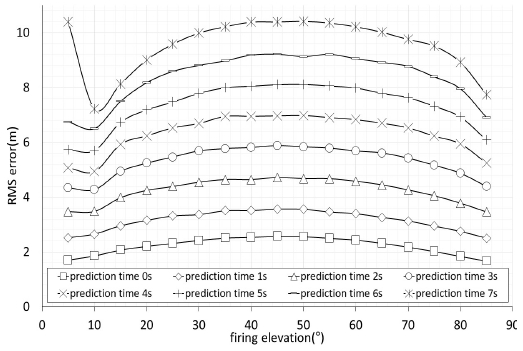
발사체는 발사 고각이 0°부터 90°까지 증가함에 따라 비행거리는 증가하다가 감소하고, 비행시간은 계속 증가한다. 이에 대한 착점 RMS 오차의 영향성을 분석하기 위해 발사체 발사 고각을 0°부터 85°까지 5° 간격으로 시뮬레이션을 수행한 결과가 다음 그림 5이다.

Fig. 5.

RMS error by firing elevation

고각 5°로 발사된 발사체의 비행시간은 약 9.3초이며, 4.5초까지는 고도가 상승하며 이후엔 하강하게 된다. 착점 진입 각도도 10° 이하로 비행속도가 빨라 발사체의 하강이 이루어지기 전부터 예측이 시작되는 경우 RMS 오차값이 크게 나온 것이라 추정된다. 발사체 발사 고각이 10° 이상이면 비행시간은 17초보다 크며, 이때는 모든 예측시간별로 RMS 오차값은 증가하다가 감소하였다. 이는 필터의 레이더 측정정보가 수렴함에 따라 방위각 오차 바이어스가 발생하여 RMS 오차값은 비행거리에 비례하는 결과가 나온 것으로 추정된다.

Ⅴ. 결론 및 향후 과제

논문에서는 레이더 측정을 이용하여 발사체의 착점을 추정하는 문제를 다루었다. 이를 위해 중력, 항력, 코리올리힘이 반영된 PMM(Point Mass Trajectory Model) 기반의 발사체 운동모델을 사용하였다. 그리고 비선형의 발사체 운동에 대해 위치만 측정되는 레이더 측정정보로부터 발사체의 속도를 추정하기 위해 1차 확장 칼만터를 사용하였고, 착점 추정을 위한 발사체 운동모델 기반 1차 확장 칼만필터를 설계하였다.

파라미터 결정을 위한 실험을 통해서 적정한 공정잡음의 표준편차 q 값은 5임을 알 수 있었다. 예측 성능 분석을 통해서는 예측시간의 길이 1초까지는 RMS 오차가 5m 내의 결과값을 보임을 확인할 수 있었다. 발사체 발사 방위별 RMS 오차 결과는 0.2m의 차이를 보였고, 풍향, 풍속별 RMS 오차 결과는 30m 이상 차이를 보였다. 이를 바탕으로 발사체 운동모델에 반영된 코리올리힘보다 풍향, 풍속에 의한 항력이 발사체의 착점 예측 오차를 크게 발생시킨다는 것을 알 수 있었다. 그리고 발사체 발사 고각을 달리한 실험을 통해서는 발사체의 착점 RMS 오차가 발사체의 비행거리에 비례함도 확인할 수 있었다.

향후 연구 과제로는 발사체 운동모델과 같은 비선형 추적을 수행하기 위해 언센티드 변환 기법을 이용한 언센티드 칼만 필터(UKF:Unscented Kalman Filter)의 설계를 통해 발사체 운동모델 기반 1차 확장 칼만필터와의 비교분석을 수행할 예정이다.

References

Tae-Il Suh and Eui-Jin Kim, "Development of Gun Fire Control System for the FFX-I Program", Journal of the KIMST, Vol. 16, No. 6, pp. 752-761, Dec. 2013. [https://doi.org/10.9766/KIMST.2013.16.6.752]
Jae-Kyung Jung and Dong-Hwan Hwang, "Estimation of Impact Point for the Ballistic Target using a Trajectory Identification", Proceeding of ICROS Daejeon Chungcheong Chapter Conference, Daejeon: KAIST, pp. 156-160, Nov. 2014.
Sang-hyuk Park and Chang-Kyung Ryoo, "State Estimation and Trajectory Prediction of a Ballistic Missile", Korea Automatic Control Conference, Busan: BEXCO, pp. 149-154, Sep. 2009.
Byung-soo Kim, "Precision Guided Munitions development and current situation of technique", Journal of the KSME, Vol 50, No. 4, pp. 36-41, Apr. 2010.
Woo-sung Park and Chang-Kyung Ryoo, Yong-ho Kim, and Jong-ju Kim, "A Guidance Law to Maintain Ballistic Trajectory for Smart Munitions", Journal of the Korean Society for Aeronautical & Space Sciences, Vol. 39, No. 9, pp. 839-847, Sep. 2011. [https://doi.org/10.5139/JKSAS.2011.39.9.839]
Seok-hyun Shin and Jong-ju Kim, "A Precise Projectile Trajectory Registration Algorithm Based on Weighted PDOP", Journal of the Korean Society for Aeronautical & Space Sciences, Vol. 44, No. 6, pp. 502-511, Jun. 2016. [https://doi.org/10.5139/JKSAS.2016.44.6.502]
Farina Alfonso and Branko Ristic, Dario Benvenuti, "Tracking a ballistic target: comparison of several nonlinear filters", IEEE Transactions on aerospace and electronic systems, Vol. 38, No. 3, pp. 854-867, Jul. 2002. [https://doi.org/10.1109/TAES.2002.1039404]
Seung-hwan Bae, "Prediction of Abdominal Rotational Motion Using an Extended Kalman Filter", The Graduate School Kyungpook National University, Jun. 2019.
AMMUNITION & EXPLOSIVES, http://www.poongsan.co.kr/eng/files/ammo-catalogue.pdf, . [accessed: Sep. 01, 2019]
STANAG 4355, Edition 2 and Draft Edition 4: Modified Point Mass and Five Degrees of Freedom Trajectory Models.
Baranowski Leszek, "Feasibility analysis of the modified point mass trajectory model for the need of ground artillery fire control systems", Journal of theoretical and applied mechanics, Vol. 51, No. 3, pp. 511-522, Jul. 2013.
Yong-su Cheong, "A Multiple Model of Target Motions for 3D Tracking", The Graduate School Kyungpook National University, Jun. 2019
Mass precision measurement technology, http://www.kasto.or.kr/files/down12/2006211/1%C0%E5.pdf, [accessed: Sep. 01, 2019]
Rui Fonte-Boa and José Borges, and José Chaves, "Analysis of external ballistics for aprojectile of caliber 155mm", Proelium, Vol. 7, No. 12, pp. 227-241, 2017.
Runge-Kutta Methods, http://web.mit.edu/10.001/Web/Course_Notes/Differential_Equations_Notes/node5.html, . [accessed: Sep. 01, 2019]
Y. Bar-Shalom, "Estimation with Applications to Tracking and Navigation", Wiley-Interscience, pp. 274-275, 2004.

저자소개

강 봉 수 (Bong-Soo Kang)

2010년 2월 : 경북대학교 전자공학(공학사)

2020년 2월 : 경북대학교

전자공학(공학석사)

2010년 1월 ~ 현재 : 한화시스템(주) 전문연구원

관심분야 : 전투체계, 사격통제

이 인 수 (In-Soo Lee)

1986년 : 경북대학교 전자공학 (공학사)

1989년 : 경북대학교 전자공학 (공학석사)

1997년 : 경북대학교 전자공학 (공학박사)

1997년 3월 ~ 2008년 2월 : 상주대학교 전자전기공학부 교수

2005년 8월 ~ 2007년 1월 : 샌디에이고주립대학교, Research scholar

2008년 3월 ~ 2014년 10월 : 경북대학교 산업전자공학과 교수

2014년 11월 ~ 현재 : 경북대학교 IT대학 전자공학부 교수

관심분야 : 시스템 이상신호처리 및 고장진단, 신경회로망 기반 지능제어, 고장허용제어, 지능형센서 시스템 및 환경모니터링, 배터리 SOC 및 SOH