신경망 학습을 위한 콤팩트 유전 알고리즘
초록
이 연구는 콤팩트 유전 알고리즘(CGA)을 이용해서 다층 신경망 가중치를 최적화하는 CGANN 알고리즘에 대한 것이다. CGA는 유전 알고리즘 변형으로 모집단을 구성하지 않고, 교차와 돌연변이 같은 유전연산을 사용하지 않으며, 원형벡터를 사용해서 염색체를 생성한다. CGANN에서 원형벡터는 염색체를 구성하는 유전자 즉, 신경망을 구성하는 가중치들이 특정 값을 취할 확률을 저장한 벡터이고, CGA는 이것을 학습하여 신경망을 최적화한다. Kaggle의 Fruits360 이미지 데이터 세트를 활용해서, 이미지 분류 문제를 위한 신경망에 CGANN을 적용한 결과, 학습계수에 따라, 일반적인 유전 알고리즘을 결합한 GANN 이상의 정확도로 학습할 수 있음을 확인할 수 있었다.
Abstract
This study is about the CGANN algorithm, which uses compact genetic algorithms to optimize multi-layer neural network weights. CGA is a variation of the genetic algorithm that does not construct a population sets and genetic operations like crossover and mutation but uses a prototype vector to generate chromosomes. In CGANN, the prototype vector is a vector storing the probability that the genes that make up a chromosome i.e. weights constituting the neural network take a specific value, and the CGA learns this to optimize the neural network. Using Kaggle's Fruits360 image data set, CGANN was applied to neural networks for image classification problems, and it was found that, according to learning coefficient, it could be trained with more accuracy than GANN combined with common genetic algorithms.
Keywords:
compact genetic algorithms, neural networks, soft computing, hybrid algorithms, quantum computingⅠ. 서 론
딥러닝을 포함한 신경망에 대한 연구가 활발해지면서, 신경망과 유전 알고리즘을 결합한 하이브리드 알고리즘에 대한 연구가 다시 시작되었다. 보통 이런 방법은 수행 시간이나 기억장소 사용 측면에서 비용이 큰 것으로 알려져 크게 주목받지 않았다.
가장 일반적인 신경망과 유전 알고리즘 결합 방법은 유전 알고리즘을 이용해서 응용문제에 적합한 신경망 구조와 매개변수를 찾는 것이다. 이런 유형의 연구는 오래전부터 진행되어 왔으며 특히 다양한 인코딩 방법에 대해서 이미 연구가 잘 이루어졌다[1]-[5]. 최근에는 중첩신경망 같은 딥러닝에 유전 알고리즘을 적용하는 하이브리드 알고리즘에 대한 많은 연구 결과가 보고되고 있다[6]-[9].
신경망에 유전 알고리즘을 적용하는 다른 방법은 학습 자체에 유전 알고리즘을 적용하는 것이다. 즉, Adam 옵티마이저 같은 오류역전파에 기초한 학습 알고리즘을 사용하는 대신 유전 알고리즘을 옵티마이저로 사용하는 방법이다[5][10]. 최근 우버 인공지능 랩 연구 결과에 따르면 특히 강화학습을 위한 딥 뉴럴 네트워크 학습에, 오류역전파 같은 기울기 강하에 기초한 알고리즘 대신, 모집단을 기초로 하는 유전 알고리즘을 사용하는 게 경쟁력 있는 대안이 될 수 있는 것으로 보인다[11].
자연의 진화를 모방한 유전 알고리즘은 모집단을 기초로 자연 선택과 유전 연산에 의해 최적화가 이루어진다. 서두에 언급한 것처럼 신경망에 유전 알고리즘을 결합하는 경우 모집단 구성에 의한 기억장소 비용이 문제로 인식되어왔다. 특히 딥러닝 응용 분야와 같이 신경망의 규모가 큰 경우 기억장소 문제가 부담이 될 수 있다[12].
이 연구는 모집단을 별도로 구성하지 않는 콤팩트 유전 알고리즘(CGA, Compact Genetic Algorithms)을 사용해서 다층 신경망을 학습하는 하이브리드 알고리즘에 대한 것이다. 먼저 CGA를 간략하게 살펴보고, 신경망과 CGA를 결합한 CGANN(CGA for Neural Networks) 알고리즘을 제시한 후, 이미지 인식 문제에 적용해서 결과를 분석해 본다.
Ⅱ. 신경망 학습을 위한 CGA
이 장에서는 먼저 신경망 학습에 유전 알고리즘을 적용하는 통상적인 방법을 알아보고, CGA와 신경망과 CGA를 결합한 CGANN 알고리즘을 상세하게 설명한다.
2.1 신경망 학습을 위한 유전 알고리즘
이 연구는 다층 신경망의 가중치를 유전 알고리즘으로 최적화하는 것을 다루므로 신경망 구조나 매개변수를 최적화하는 내용은 언급하지 않는다. 다만 최적의 신경망 구조를 찾기 위해 신경망을 인코딩 하는 방법에 대한 이슈는 [4][5]에 잘 나와 있으며, 딥러닝을 위한 신경망 구조 최적화에 대한 많은 연구가 [6]-[9]에 잘 나와 있음을 다시 밝힌다.
신경망 가중치를 유전 알고리즘으로 직접 최적화하는 방법은 다음과 같이 아주 간단하다.
- GANN
- 1. 문제에 적절한 신경망 구조를 결정한다.
- 2. 초기모집단을 구성한다.
- 3. 입력을 전파하여 적합도를 계산한다.
- 4. 종료조건에 도달하면 종료한다.
- 5. 교차 및 돌연변이 등 유전연산 적용 후 3으로 이동 한다.
먼저 문제에 적절한 신경망 구조를 결정해야 한다. 예를 들어, 입력-중간1, 중간1-중간2, 중간2-출력 층이 각각 10×12, 12×8, 8×4 차원인 구조의 신경망을 학습하는 경우, 해당 크기의 행렬 3조가 모집단의 후보 해 즉, 염색체 하나에 대응된다. 신경망 구조가 정해지면 정해진 크기의 초기 모집단을 임의로 구성한다. 다음으로 해당 가중치를 갖는 신경망에 입력을 전파하여 출력을 계산한 후 목표 출력과 비교해서 적합도를 계산한다. 종료조건에 도달한 염색체가 없는 경우 유전연산을 적용해야 하는데 염색체가 결국 실수 벡터이므로 유전연산 역시 보통의 교차와 돌연변이를 사용할 수 있다[10].
2.2 콤팩트 유전 알고리즘
신경망 가중치를 학습할 콤팩트 유전 알고리즘을 살펴보자. CGA는 자연의 진화에서 영감을 얻은 진화연산의 일종으로 분포 추정 알고리즘 계열이자, 모집단 구성 유전 알고리즘의 변형이다[13]. 이 알고리즘은 모집단을 구성하는 대신, 확률에 의해 염색체를 생성하는 원형벡터를 사용한다. 원형벡터는 후보해를 나타내는 염색체를 생성하기 위해 각 유전자가 특정 값을 가질 확률을 저장한 벡터로 크기는 염색체의 크기와 같다. 예를 들어, 염색체의 길이가 10비트 이진 비트 벡터면 원형벡터의 크기는 10개의 실수 값을 갖는 벡터이고 각각은 특정 비트가 1일(또는 0일) 확률을 나타낸다. CGA는 후보 염색체의 적합도에 따라 각 유전자가 취할 수 있는 값의 확률을 수정하는 방식으로 진화한다. 이 연구에서 사용하는 CGA는 다음과 같다[13][14].
- CGA
- 1. 원형벡터 V 무작위 생성한다.
- 2. 염색체 S1, S2 무작위 생성(V 이용)한다.
- 3. 적합도 계산 후 승자 Sw와 패자 Sl 결정한다.
- 4. V의 각 유전자에 대해 반복한다.
- 인 경우,
- 이면
- 아니면
- 5. 종료조건에 도달하지 않으면 2로 간다.
CGA 알고리즘에서 염색체는 비트 벡터이고, 원형벡터는 각 유전자가 1일 확률, 그리고 목적함수를 최소화하는 경우로 가정하자. 먼저 각 유전자가 1일 확률을 임의로 정해 원형벡터를 생성한다. 다음으로 후보 염색체 2개를 생성해서 승자와 패자를 정한 후, 더 적합한 염색체의 해당 유전자의 출현 확률을 높인다. 즉, 각 유전자가 1 또는 0을 취할 수 있으므로 1이면서 더 좋으면 1/α를 더해서 크게, 0이면서 1/α를 빼서 더 좋으면 작게 한다. α는 학습량을 조절하는 학습계수다.
CGA는 유전 알고리즘의 절차를 따르지만 모집단을 별도로 구성하지 않고, 교차나 돌연변이를 사용하지 않는다는 점에서 보통의 유전 알고리즘과 다르다. CGA의 성능 등 자세한 특징은 [14]에 잘 나타나있다.
2.3 신경망 학습을 위한 CGANN
이제 신경망 학습을 위해 CGA를 어떻게 결합할 수 있는지 논의해 보자. CGANN 절차는 GANN과 크게 다르지 않다. 가장 큰 차이는 모집단을 구성하지 않는 것, 교차와 돌연변이 같이 염색체를 대상으로 유전 연산을 적용하지 않는다는 것으로 요약할 수 있다. CGANN의 전체적인 절차는 다음과 같다.
- CGANN
- 1. 문제에 적절한 신경망 구조를 결정한다.
- 2. 원형벡터 V 무작위 생성한다.
- 3. 염색체 S1, S2 무작위 생성(V 이용)한다.
- 4. 적합도 계산 후 승자 Sw와 패자 Sl 결정한다.
- 5. V의 각 유전자에 대해 반복한다.
- 인 경우,
- 이면
- 아니면
- 6. 종료조건에 도달하지 않으면 3으로 간다.
GANN과 비교해보면, 초기모집단을 구성하는 대신, 원형벡터 V를 무작위로 생성하는 것으로 시작한다. 다음으로 염색체 S1, S2를 역시 무작위로 생성하는데, 이들 각각이 하나의 신경망에 해당한다. 따라서 입력을 전파한 후 오차를 계산해서 두 후보 중 승자와 패자를 정할 수 있다. 이제 유전연산 단계에 해당하는데, CGA는 염색체를 대상으로 돌연변이나 교차 같은 연산을 적용해서 새로운 개체를 생성하는 게 아니라, 앞에서 언급한 방식으로 원형벡터의 확률을 최적화한다. 이 연구의 경우 신경망 구조는 최적화 대상이 아니므로 두 염색체는 동일한 크기의 벡터다. 실제로 신경망의 경우 가중치는 행렬로 표현되지만 일반성을 잃지 않고 실수 벡터로 나타낼 수 있고, 위 알고리즘의 단계 5. 절차를 무리 없이 수행할 수 있다. 특정 문제에 CGANN을 적용할 때 이러한 변환과 관련된 이슈는 다음 3장에서 구체적으로 다룬다.
Ⅲ. 성능 평가 및 분석
이제 특정 이미지 분류 문제를 위한 CGANN을 구현해서 이 알고리즘을 사용하는데 필요한 절차를 구체적으로 알아보고 학습 정확도를 분석해보자.
3.1 이미지 분류 문제와 신경망 구조
실험에 사용할 문제는 Kaggle의 Fruits360 이미지 데이터 세트를 이용한 이미지 분류다. Fruits360은 사과, 아보카도, 바나나, 체리, 레몬, 키위, 망고, 라즈베리 같은 과일 60 클래스를 포함한다. Ahmed Gad는 이 데이터 세트를 사용해서 신경망과 유전 알고리즘을 결합한 하이브리드 알고리즘을 연구했다[15]. 그의 연구는 60개 클래스 중 사과, 레몬, 망고, 라즈베리의 4 클래스 이미지를 분류대상으로 하고, 각 클래스에 대해 학습용 491개, 검증용 162개 이미지를 사용했으며, 크기 100×100인 원래의 이미지에 대한 히스토그램 분석을 통해 102개의 특징을 추출해서 입력 데이터로 사용하였다. 우리 연구에서도 이렇게 가공된 데이터를 동일하게 사용한다. 따라서 우리가 학습할 신경망은 입력 뉴런 102개, 출력 뉴런 4개다. 중간층의 개수와 각 중간층 뉴런의 개수는 임의로 정해야 한다. [15] 연구의 경우 각각 150개와 60개 뉴런을 갖는 중간층 2개를 사용하였다. 이 연구에서도 비교의 편의를 위해 동일한 신경망 구조를 사용하기로 한다.
3.2 이미지 분류를 위한 CGANN 구현
특정 문제에 유전 알고리즘을 적용하는 경우 사용자가 해야 할 2가지는 적합도 함수 설정과 염색체 인코딩이다. CGANN을 구현하는 경우도 크게 다르지 않다. 적합도 함수는 다음과 같이 정의할 수 있다.
| (1) |
CGA는 최적화 대상이 원형벡터다. 원형벡터는 각 성분이 염색체 상의 대응 유전자가 특정 값(보통 1)을 취할 확률인 벡터이고, 이 실험 문제의 경우 원형벡터를 사용해서 생성한 염색체는 이미지 분류를 위한 신경망의 가중치를 나타내야 한다. 먼저 염색체를 살펴보자. 3.1에서 설명했듯이 이 실험의 신경망 구조는 크기가 102×h1×h2×4이다. 따라서 하나의 염색체는 입력-중간1, 중간1-중간2, 및 중간2-출력 층 가중치 행렬 3조에 해당하는 실수 값을 나타내야 한다. 예를 들어, [15]처럼 h1=150, h2=60인 경우, 102×150+150×60+60×4=24,540개의 실수 값으로 구성된다. 마지막으로 고려할 사항은 원형벡터가 비트 벡터를 생성한다는 점이다(2.2 참조). CGA는 원형벡터가 생성한 염색체의 유전자가 1일 확률을 높이거나 낮추는 방식으로 최적화가 이루어진다. 따라서 전체 가중치가 모두 n개인 신경망에 대해 실수 값을 m비트 스트링으로 인코딩하는 경우 하나의 염색체는 n×m비트 벡터로 나타낼 수 있다. 즉, 이 실험 문제의 경우 크기 102×h1×h2×4×m인 비트 벡터이고, 따라서 원형벡터는 같은 크기의 실수 벡터다.
CGANN 실행 과정을 요약하면, 먼저 0 ~ 1사이의 값을 성분으로 하는 원형벡터를 임의로 생성한 후, 후보 염색체 2개를 생성한다. 각각을 신경망 구조에 맞게 (이 실험의 경우 3개조) 행렬로 변환한 후, 신경망 출력을 산출하여 적합도를 계산해서, 승자와 패자를 정하고, CGANN 절차 5에 따라 원형벡터를 갱신하는 과정을 반복한다.
3.3 CGANN 평가 및 분석
파이참 2019 개발환경에서 파이썬 3.7로 구현하였으며 윈도우즈 운영체제, i7에서 실행하였다.
일반적인 유전 알고리즘을 이용한 방법과 비교하기 위해 먼저 [15]에 구현한 GANN의 학습 정확도를 측정하였다. 신경망 구조는 중간층 뉴런이 각각 150×60, 100×40인 경우이고, 초매개변수는 다음 표 1과 같다.
10회 반복 실행한 결과는 다음 표 2와 같다. 학습 실패로 간주할 수 있는 정확도 60 이하를 배제한 평균은 각각 84.5와 79.6이다.
CGANN 역시 두 중간층 뉴런이 각각 150×60, 100×40인 경우를 사용했으며, 초매개변수는 다음 표 3과 같다.
CGANN은 모집단을 구성하지 않으며, 교차와 돌연변이 대신 학습계수 α에 의해 원형벡터를 수정하는 방식으로 학습이 이루어지므로 모집단의 크기나 유전연산을 위한 초매개변수가 없다. 대신 CGANN은 학습계수 α가 정확도에 영향을 준다[14]. 학습계수 α를 달리해가면서 각각 10회 반복 실행한 결과는 다음 표 4와 같다.
동일한 신경망 구조에 대해 CGANN을 적용했을 때 평균 정확도가 대체로 높다(특히 학습계수 α = 10인 경우 정확도가 상대적으로 더 높음). 따라서 CGA를 다층 신경망 최적화에 응용할 수 있음이 확인되었다.
CGANN을 사용해서 신경망을 최적화하는 경우 신경망 구조와 학습계수 α의 관계에 대한 세밀한 주의가 있어야하겠다. 표 4를 보면 대체로 신경망 구조가 작은 경우 학습이 불안정해 보인다. 특히 평균 정확도가 가장 높은 α = 10의 경우, 정확도가 60이하인 경우가 3회 있었다. 따라서 신경망 구조가 적절하지 않은 경우 반대로, 학습계수가 적절하지 않은 경우 최적화가 어려울 수 있겠다. 그러나 이런 특징을 CGANN의 특이한 결함으로 보기는 어렵다. 실제로 GANN의 경우는 물론이고, 역전파 알고리즘을 사용하는 경우조차, 신경망 구조, 심지어 초기 가중치의 범위에도 매우 민감한 특징을 갖는다.
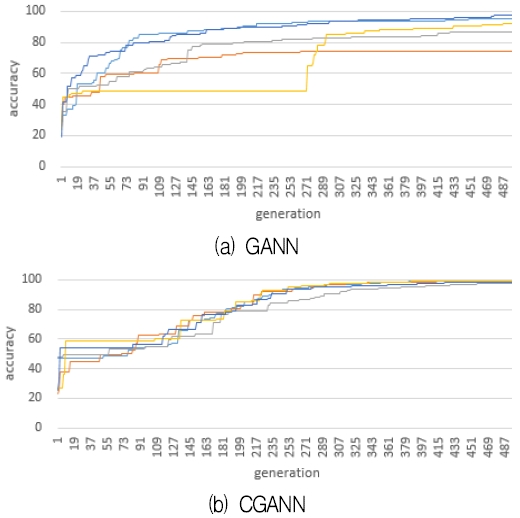
다음 그림 1은 학습 반복횟수 500세대에 도달할 때까지 적합도 즉, 신경망의 학습 정확도 증가 추세를 나타낸다. 중간층 크기는 모두 150×60이며CGANN의 학습계수 α는 10이고, 다른 초매개변수는 GANN과 CGANN에 대해 각각 앞과 동일하게 설정하였다. 5회 반복 실행한 결과 정확도 평균은 GANN이 89.2%이고 CGANN이 98.8%이었다. 신경망의 크기나 다른 초매개변수를 어떻게 설정하느냐에 따라 다소 다르기는 하겠으나, CGANN의 경우 학습 반복횟수가 늘어남에 따라 학습 정확도가 최대 99.4%인 경우도 있다.
5회 반복한 실행 결과는 다음 표 5와 같다. 이 결과는 표 2, 4의 경향과 대체로 일치하며, 해당 초매개변수에 대해 반복횟수가 늘어날수록 CGANN이 더 안정적으로 수렴함을 알 수 있다.
Ⅳ. 결 론
딥러닝 등 신경망과 유전 알고리즘을 결합하는 연구가 활발하게 진행되고 있다. 이 연구는 콤팩트 유전 알고리즘 즉, CGA를 이용해서 다층 신경망 가중치를 최적화(학습)하는 CGANN 알고리즘을 제시하고 학습 정확도를 분석하였다. 유전 알고리즘을 변형한 CGA는 모집단을 구성하지 않고, 교차 및 돌연변이 같은 유전연산도 사용하지 않으며, 염색체의 구성요소 즉, 유전자가 특정 값을 취할 확률을 저장한 원형벡터를 학습하는 방법으로 최적화를 수행한다. CGA는 모집단을 구성하지 않으므로 기억장소 비용이 중요한 응용에 사용할 수 있고, 효과적인 링키지 학습으로 단순 유전 알고리즘보다 더 빠르고 정확한 방법으로 알려졌다[16]. Kaggle의 Fruits360 이미지 데이터 세트를 활용해서, 이미지 분류 문제를 위한 신경망에 CGANN을 적용한 결과, 일반적인 유전 알고리즘을 결합한 GANN 이상의 정확도로 학습할 수 있음을 확인할 수 있었다. 중첩신경망 같은 딥러닝은 일련의 중첩층과 풀링층에 이어 마지막으로 분류나 회귀를 위한 완전연결층을 거쳐 출력을 산출한다. 완전연결층은 다층 신경망 구조이므로 중첩신경망 후반부에 CGANN을 직접 사용할 수 있다.
이 연구는 CGA와 신경망을 결합한 하이브리드 최적화 기법의 학습 정확도 분석을 주목적으로 하여, 효율적인 수행시간 및 기억장소 사용을 위한 구현 기술은 이 논문에 포함하지 않았다. 이 연구의 경우 원형벡터가 생성하는 염색체가 비트 벡터인 경우로 가정했다. 따라서 염색체를 신경망 연결 가중치에 대응하는 실수 벡터로 변환하는 과정과 반대 과정이 필요하며, 따라서 이러한 처리에 따른 수행시간 분석이 추가로 수행될 필요가 있다. 한편, 이러한 방법이 신경망 학습에 CGA를 결합하는 유일한 표현방법은 아니다. 원형벡터가 실수 벡터를 생성하는 대신, 원형벡터 학습 즉, 진화의 전략을 새로 개발 할 수 있겠고, ECGA와 ES를 결합하는 관련 연구를 수행 중이다. 신경망 학습을 위해 기울기에 기초한 역전파 알고리즘 대신 유전 알고리즘을 사용하는 경우, 기울기 소실 문제가 발생하지 않는다. 따라서 CGANN을 깊은 신경망 구조에 적용하는 연구 역시 수행 중에 있다. 또한, CGA에서 원형벡터는 염색체의 유전자가 가능한 값을 동시에 갖게 한다. 이 개념은 양자 컴퓨팅 잘 어울린다. CGANN을 양자컴퓨터에서 실행하는 방법을 연구 중이다.
Acknowledgments
이 논문은 2019년도 강릉원주대학교 전임교원 연구년 지원에 의하여 수행되었음
References
-
D. Fogel, L. Fogel, and V. Porto, "Evolving neural networks", Biological Cybernetics, Vol. 63, pp. 487-493, Oct. 1990.
[https://doi.org/10.1007/BF00199581]

-
J. Arifovica and R. Gencay, "Using genetic algorithms to select architecture of a feedforward artificial neural network", Physica A: Statistical Mechanics and its Applications, Vol. 289, No. 3-4, pp. 574-594, Jan. 2001.
[https://doi.org/10.1016/S0378-4371(00)00479-9]

-
J. Idrissi, R. Hassan, G. Youssef, and E. Mohamed, "Genetic algorithm for neural network architecture optimization", 2016 3rd International Conference on Logistics Operations Management (GOL), Fez, Morocco, pp. 1-4, May 2016.
[https://doi.org/10.1109/GOL.2016.7731699]

- P. Koehn, "Combining Genetic Algorithms and Neural Networks: The Encoding Problem, A Thesis for the MS Degree", The University of Tennessee, 1994.
-
H. Chiroma and Ahmad Shukri Mohd Noor, et al., "Neural Networks Optimization through Genetic Algorithm Searches: A Review", Applied Mathematics and Information Sciences, Vol. 11, No. 6, pp. 1543-1564. Nov. 2017.
[https://doi.org/10.18576/amis/110602]

-
E. David and I. Greental, "Genetic Algorithms for Evolving Deep Neural Networks", ACM Genetic and Evolutionary Computation Conference (GECCO), Vancouver, Canada, pp. 1451-1452, Jul. 2014.
[https://doi.org/10.1145/2598394.2602287]

-
Y. Zhining and P. Yunming, "The Genetic Convolutional Neural Network Model Based on Random Sample", International Journal of u- and e- Service, Science and Technology, Vol. 8, No. 11, pp. 317-326, Nov. 2015.
[https://doi.org/10.14257/ijunesst.2015.8.11.31]

- A. Bhandare and D. Kaur, "Designing Convolutional Neural Network Architecture Using Genetic Algorithms", Proceedings on the International Conference on Artificial Intelligence (ICAI), Las Vegas, USA, pp. 150-156, Aug. 2018.
-
M. Suganuma, S. Shirakawa, and Tomoharu Nagao, "A Genetic Programming Approach to Designing Convolutional Neural Network Architectures", Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18, Stockholm, Sweden, pp. 5369-5373, Jul. 2018.
[https://doi.org/10.24963/ijcai.2018/755]

-
Z. Liu, A. Liu, C. Wang and Z. Niu, "Evolving neural network using real coded genetic algorithm (GA) for multispectral image classification", Future Generation Computer Systems, Vol. 20, No. 7, pp. 1119-1129, Oct. 2004.
[https://doi.org/10.1016/j.future.2003.11.024]

- F. P. Such and V. Madhavan, et al., "Deep Neuroevolution: Genetic Algorithms are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning", Uber AI Labs, 2018.
- T. Chen, B. Xu, C. Zhang, and C. Guestrin, "Training Deep Nets with Sublinear Memory Cost", arXiv:1604.06174v2, [cs.LG] 22 Apr. 2016.
- Brownlee and Jason, "Clever algorithms : nature-inspired programming recipes", 5.4 Compact Genetic Algorithm, 2011.
-
G. R. Harik, F. G. Lobo, and D. E. Goldberg, "The Compact Genetic Algorithm", IEEE Transactions on Evolutionary Computation, Vol. 3, No. 4, pp. 287-297, Nov. 1999.
[https://doi.org/10.1109/4235.797971]

- A. Gad, https://towardsdatascience.com/artificial-neural-networks-optimization-using-genetic-algorithm-with-python-1fe8ed17733e, , 2019. [accessed; Oct. 01. 2019]
- G. R. Harik, "Linkage Learning via Probabilistic Modeling", IlliGAL Technical Report 99010, Jan. 1999.

1985년 : 연세대학교 수학과 (이학사)
1988년 : 고려대학교 전산과학과 (이학사)
1991년 : 고려대학교 수학과 (이학석사)
1996년 : 고려대학교 컴퓨터학과 (이학박사)
1997년 ~ 현재 : 강릉원주대학교 컴퓨터공학과 교수
관심분야 : 복잡계, 인공생명, 인공지능, 소프트컴퓨팅