[ Article ]

The Journal of Korean Institute of Information Technology - Vol. 18, No. 1, pp.49-55

ISSN: 1598-8619 (Print) 2093-7571 (Online)

Print publication date 31 Jan 2020

Received 24 Oct 2019 Revised 14 Nov 2019 Accepted 17 Nov 2019

DOI: https://doi.org/10.14801/jkiit.2020.18.1.49

대용량 다중 입력 다중 출력 시스템에서 코드북 갱신 기반의 새로운 계층적 다중 빔 검색 방법

윤성근^*

; 이승준^**

*강원대학교 BIT 의료융합학과 박사과정
**강원대학교 IT 대학 전자공학과 및 BIT 의료융합학과 교수(교신저자)

A Novel Hierarchical Multi-Beam Search Scheme Based on Codebook Update for Massive MIMO Systems

Sung-Geun Yoon^*

; Seung Joon Lee^**

Correspondence to: Seung Joon Lee Dept. of Electronics Engineering, Kangwon National University Chunchenon, Gangwon-do, 200-701 Korea, Tel.: +82-33-250-6300, Email: s.j.lee@kangwon.ac.kr

초록

본 논문에서는 대용량 다중 입력 다중 출력(Massive MIMO) 시스템에서 다중 데이터 스트림 전송을 위한 계층적 코드북 기반 빔 검색에 관하여 연구하였다. 다중 데이터 스트림을 동시에 전송하기 위해 빔들을 순차적으로 검색해야 하는 다중 빔 검색의 경우, 각 빔 검색에서 이미 선택된 빔이 다음 빔 검색에 미치는 영향을 고려하여야 한다. 따라서 본 논문에서는 이미 선택된 빔의 영향을 고려한 기존의 다중 빔 검색 방법을 검토하고 그 방법의 문제점을 분석하였다. 기존 방법의 문제점을 극복하기 위해 코드북 갱신을 이용하는 새로운 계층적 코드북 기반 다중 빔 검색 방식을 제안한다. 컴퓨터 시뮬레이션을 통해 기존 방법과 성능 비교를 실시하여 제안된 방식의 우수함을 확인하였다.

Abstract

In this paper, a hierarchical codebook based multi-beam search is studied for multiple stream transmission in the massive MIMO systems. For the multi-beam search where multiple beams are serially searched, it is important that the effect of the already selected beams on each beam should be considered in searching for the next beams. A recently reported scheme for considering the effect of the already selected beams is reviewed and its limitation is investigated. A new hierarchical codebook-based multi-beam search scheme using a codebook update is proposed so as to mitigate that limitation. Computer simulation results are presented to verify that the proposed scheme outperforms the conventional one.

Keywords:

beamforming, hierarchical codebook, hybrid precoding, massive MIMO, millimeter-wave, multi-beam

Ⅰ. 서 론

5G 무선통신 시스템의 주요 기술 중 하나인 밀리미터파 대용량 다중입출력(mmWave massive MIMO) 시스템은 큰 대역폭과 높은 빔포밍(Beamforming) 이득을 활용한다[1]. 이 시스템에서 아날로그 빔포밍과 디지털 프리코딩(Precoding) (혹은 컴바이닝(Combining))을 혼합하여 사용하는 하이브리드 프리코딩 구조가 성능과 복잡성 간의 균형을 맞추는 기술로 널리 사용되고 있다[2][3]. 특히 공간 도메인에서 동시에 다중 데이터 스트림을 전송하기 위해 아날로그 빔포밍이 아닌 하이브리드 프리코딩이 필요하다.

하이브리드 프리코딩 구조에서 채널 추정은 오직 아날로그 빔포밍을 통해서만 가능하기 때문에 해결하기 쉽지 않은 문제이다. 하이브리드 프리코딩 구조에서 채널 정보를 얻기 위해 압축 감지(Compressed sensing) 기반의 채널 추정[4]-[6]과 빔 트레이닝 기반의 채널 추정[7][8]의 두 가지 접근 방법이 존재한다. 본 논문에서는 빔 트레이닝을 통한 채널 추정에 중점을 둔다. 빔 검색 절차에서 검색 시간을 줄이기 위해 계층적 코드북을 이용한 계층적 다중 빔 검색 절차를 사용한다. 계층적 코드북에서는 상위계층 코드워드의 빔 폭은 하위계층 코드워드의 빔 폭보다 더 크다[7][8].

다중 데이터 스트림 전송을 위한 계층적 검색에 관한 연구는 [8]에서 찾을 수 있다. 다중 데이터 스트림 전송을 위한 다중 빔들은 순차적으로 탐색되는데, 이 과정에서 이미 선택된 빔들의 영향을 고려하는 것이 중요하다. 이것을 위해 [8]에서는 다른 데이터 스트림 전송을 위해 이미 선택된 빔에 영향을 준 채널 성분을 원래의 채널 행렬에서 삭제하려 하였고, 이렇게 수정된 채널 행렬을 기반으로 새로운 데이터 스트림 전송을 위한 빔 검색을 수행하였다. 본 논문에서는 [8]의 계층적 다중 빔 검색 방식의 한계를 분석하고, 그 한계를 극복하여 성능을 개선하기 위해 코드북 갱신 기반의 새로운 빔 탐색 방법을 제안한다.

Ⅱ. 연구배경

2.1 하이브리드 프리코더

Massive MIMO 시스템은 N_T개의 송신(TX) 안테나, N_R개의 수신(RX) 안테나, N_S 개의 데이터 스트림을 전송하기 위한 $N T R F$ 개의 송신 RF 체인, $N R R F$ 개의 수신 RF 체인으로 구성된다. 데이터 심볼 벡터 s는 N_S×1의 크기를 가지며 $E s s H = 1 N S I N S$ 을 만족한다. I_{N_S}는 N_S×N_S 단위행렬을 나타낸다. 벡터 s는 기저대역에서 송신 디지털 프리코더 $F B B ∈ C N T R F × N S$ 를 이용하여 프리코딩 된 후, 송신 아날로그 빔 형성기 $F R F ∈ C N T × N T R F$ 와 곱해진다. F_RF를 구성하는 모든 원소는 일정한 진폭 $1 N T$ 를 가지며 F_BB는 총 전력 요구조건 $F R F F B B F r o b 2 = N S$ 를 만족해야 한다. 수신기에서 추정된 데이터 심볼 벡터 $s^$ 는 다음과 같다.

s^= P W B B H W R F H H F R F F B B s + W B B H W R F H n

(1)

여기서 $W B B ∈ C N R R F × N S$ 는 수신 디지털 컴바이너이고, $W R F ∈ C N R × N R R F$ 은 수신 아날로그 빔 형성기이다. H는 채널 행렬이며, n은 평균이 0 분산이 σ²I_{N_R}인 복소 가우시안 잡음 벡터이다. W_RF의 모든 원소의 진폭은 $1 N R$ 의 값을 가지며 $W R F W B B F r o b 2 = N S$ 를 만족한다. 만약 W_RF의 모든 열이 서로 직교하고, W_BB가 비특이 정방행렬이면서 $N S = N R R F$ 이면, 전송속도는 다음과 같다[8, 식 (4)].

R = log 2 ⁡ I N S + P N S σ n 2 R n - 1 H e q F B B F B B H H e q H

(2)

여기서 $H e q = W R F H H F R F$ 이다. 전송속도를 최대화하는 F_BB는 워터필링 알고리즘(Waterfilling algorithm)을 이용하여 유도할 수 있다[9].

2.2 밀리미터파 MIMO 채널모델

밀리미터파 채널을 위해 널리 사용되는 Saleh-Valenzuela 모델은 다음과 같이 정의된다[3][10][11].

H = N T N R L ∑ l = 1 L α 1 a N T, ϕ l a H N T, ϕ l

(3)

L은 채널경로의 수이며 α_l은 l번째 경로에서 평균이 0이고 단위 분산을 가지는 복소 가우시안 이득을 나타낸다. θ_l과 ϕ_l은 각각 l번째 경로의 도래각(AoA)과 발사각(AoD)을 나타내며, 이 값은 [0, 2π)의 균일한 분포를 가진다. a(N, ϵ)은 등간격 선형 배열 안테나의 배열 응답 벡터로 다음과 같이 주어진다.

a N, ϵ = 1 N 1, e j 2 π λ d sin ⁡ ϵ, e j 2 2 π λ d sin ⁡ ϵ, …, e j N - 1 2 π λ d sin ⁡ ϵ T

(4)

여기서 λ는 신호의 파장이며 d는 안테나 간 거리이다.

2.3 계층적 코드북

계층적 코드북은 U의 계층으로 구성된다. u번째의 계층은 (u = 1,2,…,U), M^u개의 코드워드c(u,n) (n = 1,2,…M^u)으로 구성되어있다. M은 계층적 코드북 구조에서 하나의 상위 코드워드에 포함되어 있는 하위 코드워드의 수이다. 이는 빔 폭을 기준으로 정의되는데, 각도 도메인에서 모든 m에 대한 c(u+1,(n-1)M+m)_{m = 1,2,…M}의 빔 폭의 합은 c(u,n의 빔 폭과 일치한다. 이때 c(u,n)를 부모(Parent) 코드워드라 하고 모든 m에 대한 c(u+1,(n-1)M+m)_{m = 1,2,…M}의 코드워드를 자식(Child) 코드워드라 한다.

계층적 코드북을 이용한 계층적 검색 절차는 총 U단계로 이루어진다. 첫 번째 단계에서 송수신 각각 M개의 코드워드 중 가장 큰 빔포밍 이득을 가지는 송수신 코드워드 쌍이 첫 번째 계층에서 선택된다. u번째 단계에서는 (u = 2,3,…,U) u-1번째 단계에서 선택된 송수신 각각 코드워드의 M개의 자식 코드워드 중 가장 큰 빔포밍 이득을 가지는 송수신 코드워드 쌍이 선택된다. 이 검색 절차에서 성능 향상을 위해 첫 번째 계층이 아닌 u₀계층 (u₀ ≥ 2)의 M^u₀개의 코드워드부터 검색을 시작할 수도 있다.

2.4 기존의 계층적 다중 빔 검색에 대한 분석

단일 데이터 스트림 전송을 위해서는 한 쌍의 송수신 코드워드를 필요로 하지만, 공간 도메인에서 동시에 다중 데이터 스트림을 전송하기 위해서는 여러 쌍의 송수신 코드워드가 필요하다. 빔 탐색시간을 줄이기 위해 송수신 빔 쌍을 순차적으로 검색한다.

참고문헌 [8]에서는 q개의 데이터 스트림 전송을 위해 선택된 코드워드들로 구성된 채널형성행렬 $H ~ (q)$ 이 다음과 같이 생성 및 갱신된다.

H ~ (q) = H ~ (q - 1) + γ q w q f q H, H ~ (0) = 0

(5)

여기서 f^(q)와 w^(q)는 각각 q번째 데이터 스트림을 위해 선택된 송수신 코드워드이며, γ^(q)는 이들 송수신 코드워드에 해당된 채널 이득이다. 위와 같은 채널형성행렬을 사용하려는 취지는 q+1번째 데이터 스트림을 위한 송수신 코드워드 검색시, 원래의 채널 H 대신에 $H - H ~ (q)$ 가 사용되게 함으로써, 이미 선택된 q개의 데이터 스트림에 해당된 송수신 코드워드 선택에 영향을 준 채널 성분이 제거되게 하는 것이다.

만약 f^(q)와 w^(q)가 각각 채널 H의 우특이벡터와 좌특이벡터인 경우에, 위의 방식을 사용하면, f^(q)와 w^(q)를 선택되게 한 채널 성분을 H에서 완벽하게 제거할 수 있다. 그러나 f^(q) (w^(q))가 우(좌)특이벡터에 충분히 근사하지 않으면 해당 채널 성분을 완벽하게 제거할 수 없다. 그 결과 (q+1)번째 빔 탐색 절차에 있어 (q+1)번째 빔을 위한 최적의 부모 코드워드가 아닌 q′(q′ ≤ q)번째 빔을 위한 최적의 부모 코드워드가 선택될 우려가 커진다. 더 나아가 q′(q′ ≤ q)번째 빔을 위해 선택된 U계층 코드워드가 다시 선택되는 상황이 발생할 수 있다.

두 개의 서로 다른 스트림을 수신기에서 구분하려면 해당 스트림의 두 송신(또한 수신) 코드워드가 상이해야 한다. 동일한 코드워드가 다시 선택되는 문제를 극복하는 간단한 방법은 다음 스트림을 위한 빔 탐색시, 이미 선택된 코드워드를 0벡터로 대체하는 방법이다. 모든 자식 코드워드가 0벡터로 대체되면 부모 코드워드도 0벡터로 대체하면 된다. 참고문헌 [8]에서는 동일한 코드워드가 다시 선택되는 문제의 해결방안에 대해 언급되지 않았지만, 본 논문 5장의 시뮬레이션에서는 참고문헌 [8]의 알고리즘의 성능을 위해 위와 같은 방법을 적용하였다.

Ⅲ. 제안된 계층적 다중 빔 검색 방법

본 논문에서 제안하는 방법은 코드북 갱신을 기반으로 하며, 갱신 이전의 최초 코드북에 특별한 제한이 없으므로 모든 코드북을 사용할 수 있다. 코드북 갱신은 다음과 같이 수행된다. 만약 특정 데이터 스트림 전송을 위해 c(U,n_U)가 선택된 코드워드라고 하면, 다음 데이터 스트림 전송을 위한 빔 검색 이전에 코드북 내의 모든 계층의 코드워드 c(u,n)은 다음과 같이 c_new(u,n)로 갱신된다. u = (u₀,…,U)

c^u, n = c u, n - c H U, n U c u, n c U, n

(6a)

c^u, n ≠ 0 이 면, c n e w = c ̯ u, n c ̯ u, n = 1 c ̯ u, n c u, n - c H U, n U c u, n c ̯ u, n c U, n U

(6b)

c^u, n = 0 이 면, c n e w = 0

(6c)

(6a)에서 우변의 두 번째 항은 c(U,n_U)에 대한 c(u,n)의 투영을 의미하고, 따라서 $c^u, n$ 은 c(U,n_U)과 수직이다.

제안된 코드북 갱신에 기반한 계층적 다중 빔 검색의 전체적인 절차는 그림 1에 표기하였다.

Fig. 1.

Proposed algorithm

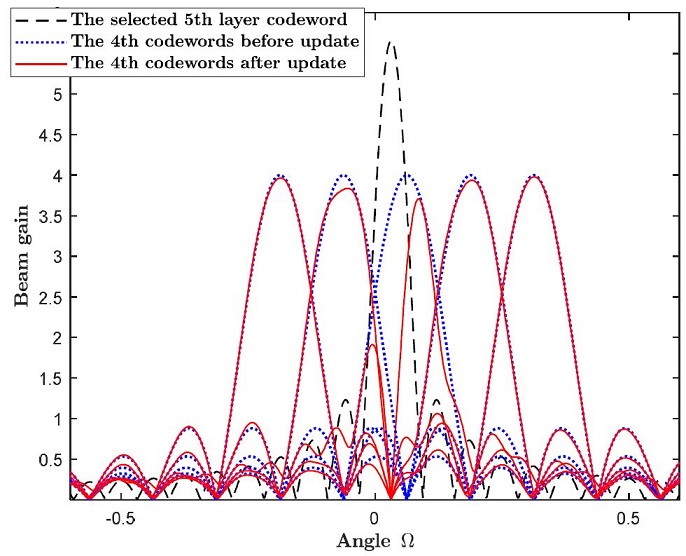
U계층의 코드워드들이 서로 직교한다면 (6)에 의해서 이미 선택된 코드워드는 0 벡터로 갱신되지만(즉, c_new(U,n_U) = 0), 동일한 계층의 다른 코드워드는 바뀌지 않는다(c_new(U,n) = c(U,n,(n ≠ n_U)). u계층에서는(u < U), U계층에서 선택된 코드워드 위치(각도 Ω 축 상의 위치)와 가까운 위치의 코드워드의 빔 모양은 식 (6)의 갱신에 의해 확연히 바뀌지만, 멀리 떨어져 있는 위치의 코드워드의 빔 모양은 거의 변경되지 않는다. 이는 그림 2에서 확인할 수 있다. 그림 1에서 안테나 수는 32개를 가정하였다. 5번째 계층에서 선택된 코드워드의 빔과 함께, 4번째 계층에서의 빔 5개(선택된 코드워드의 빔과 인접한 빔들)를 갱신 전후로 비교하였다

Fig. 2.

Beam patterns of the updated codewords

모든 계층의 초기 코드워드의 성분들은 동일한 크기(Constant modulus)를 가진다고 가정하자. q번째 (q > 1) 데이터 스트림을 위한 빔을 검색하기 위해 사용되는 갱신된 코드북에서 c_new (u,n_U) (u < U) 의 성분들은 동일한 크기를 갖지 않는다. 하지만, 이 갱신된 코드워드는 초기 코드북의 u계층의 n번째 코드워드와 U계층에서 선택된 q-1개의 코드워드들의 가중치 합이다(이 q개의 코드워드는 모두 동일한 크기 성분을 가짐). 따라서 RF 체인 한 개가 동일 크기 성분의 한 개의 코드워드의 빔을 형성한다고 하면, c_new (u,n_U) (u < U)는 최대 q개의 RF 체인을 사용하여 구현될 수 있다.

원래 N_S개의 데이터 스트림을 동시에 전송하기 위해서는 최소한 N_S개의 RF 체인이 요구된다. 빔 트레이닝 단계 동안에는 한 번에 한 개의 스트림을 위한 빔 탐색이 진행되기 때문에, 이미 준비된 N_S 개의 RF 체인으로 q번째 빔(q ≤ N_S)을 탐색하기 위한 모든 계층의 빔(갱신된 코드워드의 빔)을 구현할 수 있다. 물론, 빔 트레이닝 절차가 완료된 후의 데이터 전송 단계에서는 빔 구현을 위해 한 개의 빔(U 계층 빔)마다 한 개의 RF 체인만 필요하다. 따라서 제안된 방법에서도 데이터 전송 단계에서는 N_S의 데이터 스트림을 전송하기 위해 N_S개의 RF 체인이 사용된다.

Ⅳ. 성능평가

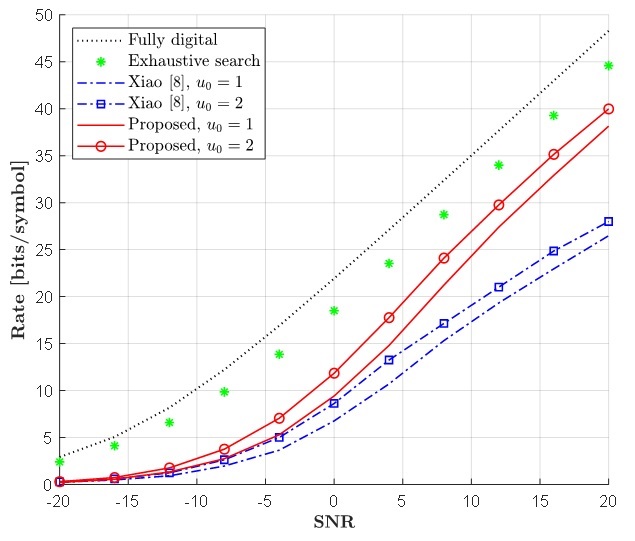
이 장에서는 제안된 계층적 다중 빔 검색 방법과 기존의 검색 방식을 전송속도 성능 측면에서 비교한다. 송수신 안테나 개수 N_T = N_R = 32, 채널 경로의 수 L = 7, 안테나 간 거리 $d = λ 2$ 를 가정하였다. 부모 코드워드마다 M = 2 개의 자식 코드워드가 있고, 데이터 스트림의 수는 송수신 RF 체인 개수와 같다고 가정한다( $N S = N T R F N R R F$ ). 제안된 방식과 기존 방식의 전송속도는 그림 3에서 N_S = 4를 가정하여 SNR에 따라 비교하였다. 여기서 이상적인 디지털 프리코딩 방식(Fully digital)과 코드북의 계층화를 사용하지 않은 완결 탐색 방식(Exhaustive search)의 성능도 포함하였다. 파라메터 u₀는 계층적 검색이 시작되는 최초계층을 나타내며, 그림 3에서 u₀ = 1과 u₀ = 2를 모두 고려하였다.

Fig. 3.

Comparison of achievable rates with varying SNR

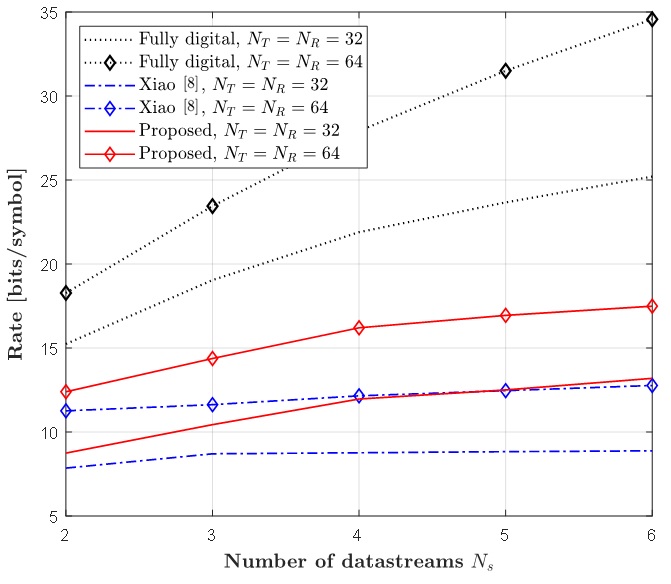
그림 4에서는 SNR = 0dB에서 데이터 스트림 개수에 따른 전송속도를 비교하였다. 또한, 안테나 개수 증가에 따른 성능 차이도 확인해 볼 수 있다.

Fig. 4.

Comparison of achievable rates with varying NS

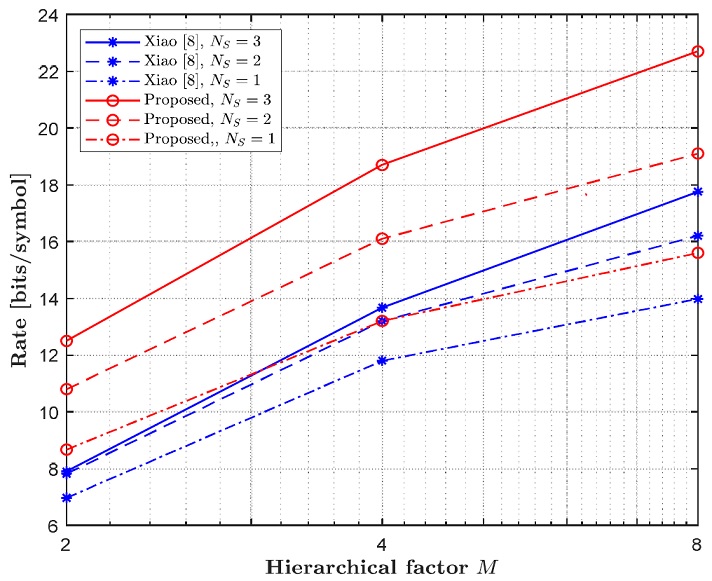
그림 5에서는 SNR = 0dB에서 M에 따른 전송속도를 비교하였다. 각각의 그림에서 볼 수 있듯이, 제안된 방식이 기존의 방식보다 훨씬 높은 전송속도를 보인다.

Fig. 5.

Comparison of achievable rates with varying M

Ⅴ. 결 론

계층적 코드북 기반 다중 빔 검색에 대한 기존 방식이 검토되었다. 기존 방식에선 선택된 송수신 빔에 의해 채널형성행렬이 구성 및 갱신되며, 이를 통해 다음 빔을 탐색할 때 이미 선택된 빔에 영향을 준 채널 성분을 가급적 제거하려고 하였다. 하지만, 특수한 경우(채널의 특이 벡터들이 모두 코드북 내에 존재하는 경우)를 제외한 실제 일반적인 상황에서는 해당 채널 성분이 잘 제거되지 않는 문제점이 있다.

본 논문에서는 기 선택된 코드워드에 영향을 준 채널 성분을 제거하는 대신에, 기 선택된 코드워드의 영향을 코드북에서 제거하는 접근 방식을 사용하였다. 이를 위해 각 계층의 코드워드에서 선택된 맨 아래 계층의 코드워드에 평행한 성분을 빼주었다. 시뮬레이션 결과를 통해 제안된 방식이 기존의 방식보다 높은 전송속도를 가짐을 확인하였다.

Acknowledgments

이 논문은 2017년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임.(No. NRF-2017R1D1A3B03032125)

References

S. Rangan, T. S. Rappaport, and E. Erkip, "Millimeter wave cellular wireless networks: Potentials and challenges", Proc. IEEE, Vol. 102, No. 3, pp. 366-385, Mar. 2014. [https://doi.org/10.1109/JPROC.2014.2299397]
R. W. Heath Jr., N. Gonzalez-Prelcic, S. Rangan, W. Roh, and A. M. ́Sayeed, "An overview of signal processing techniques for millimeter wave MIMO systems", IEEE J. Sel. Topics Signal Process, Vol. 10, No. 3, pp. 436-453, Apr. 2016. [https://doi.org/10.1109/JSTSP.2016.2523924]
A. V. Delgado, M. Sanchez-Fernandez, J. Llorca, and A. Tulino, "Feasible ́ transmission strategies for downlink MIMO in sparse millimeter-wave channels", IEEE Commun. Mag, Vol. 56, No. 7, pp. 49-55, Jul. 2018. [https://doi.org/10.1109/MCOM.2018.1701022]
A. Alkhateeb, O. E. Ayach, G. Leus, and R. W. Heath, Jr., "Channel estimation and hybrid precoding for millimeter wave cellular systems", IEEE J. Sel. Topics Signal Process, Vol. 8, No. 5, pp. 831-846, Oct. 2014. [https://doi.org/10.1109/JSTSP.2014.2334278]
Z. Marzi, D. Ramasamy, and U. Madhow, "Compressive channel estimation and tracking for large arrays in mm-wave picocells", IEEE J. Sel. Topics Signal Process, Vol. 10, No. 3, pp. 514-527, Apr. 2016. [https://doi.org/10.1109/JSTSP.2016.2520899]
Y. H. Han and J. W. Lee, "Compressed Sensing Techniques for Millimeter Wave Channel Estimation", The Journal of Korean Institute of Communicaitons and Information Sciences, Vol. 42, No. 1, pp. 25-30, Jan. 2017. [https://doi.org/10.7840/kics.2017.42.1.25]
Z. Xiao, T. He, P. Xia, and X. G. Xia, "Hierarchical codebook design for beamforming training in millimeter-wave communication", IEEE Trans. Wireless Communication Vol. 15, No. 5, pp. 3380-3392, May 2016. [https://doi.org/10.1109/TWC.2016.2520930]
Z. Xiao, P. Xia, and X. G. Xia, "Channel estimation and hybrid precoding for millimeter-wave MIMO systems: A low-complexity overall solution", IEEE Access, Vol. 5, pp. 16100-16110, July 2017. [https://doi.org/10.1109/ACCESS.2017.2724037]
E. Telatar, "Capacity of multi-antenna Gaussian channels", Europ. Trans. Telecommunication, Vol. 10, No. 6, pp. 585-595, Nov.–Dec. 1999. [https://doi.org/10.1002/ett.4460100604]
A. A. M. Saleh and R. Vlaenzuela, "A Statistical Model for Indoor Multipath Propagation", in IEEE Journal on Selected Areas in Communications, Vol. 5, No. 2, pp. 128-137, Feb. 1987. [https://doi.org/10.1109/JSAC.1987.1146527]
T. S. Rappaport, F. Gutierrez, E. Ben-Dor, J. N. Murdock, Y. Qiao, and J. I. Tamir, "Broadband millimeter-wave propagation measurements and models using adaptive-beam antennas for outdoor urban cellular communications", IEEE Trans. Antennas Propag, Vol. 61, No. 4, pp. 1850-1859, Apr. 2013. [https://doi.org/10.1109/TAP.2012.2235056]