순차적 K-means 군집화를 이용한 고차 변조 신호에 대한 채널 추정기법
초록
본 논문에서는 순차적 K-means 군집화(sequential K-means clustering, SKC) 기법을 이용하여 파일럿 신호 전송 없이 16QAM 이상의 고차 변조 신호에 대한 채널을 추정하는 기법을 제안하였다. 기존의 K-means 군집화를 이용한 채널 추정 기법은 심볼의 절댓값이 1로 일정한 QPSK에만 적용 가능하였기 때문에, 데이터 심볼을 표현하는 복소수의 절댓값이 1이 아닌 16QAM 이상 고차 변조방법에 적용할 수 없는 문제점이 있었다. 반면 본 논문에서 제안하는 SKC를 이용한 채널 추정기법은 참조 중심점이라는 새로운 중심점 설정 방법을 제시하여 기존의 군집화를 사용하는 채널 추정방법의 문제점을 해결하였다. 본 논문에서 제안하는 SKC를 이용한 채널 추정기법의 성능을 검증하기 위해서 평균 제곱 오차와 심볼 오류율을 성능 평가 지표로 사용하였다. 성능 평가 결과를 통하여 제안한 SKC를 이용한 채널 추정 기법과 참조중심점이 16QAM이상의 고차 변조 신호를 이용한 채널 추정에 성공적으로 적용됨을 확인하였으며, 파일럿 신호를 사용하고 있지 않고도 최소 제곱 채널 추정기 대비 우수한 성능을 가지고 있음을 보였다.
Abstract
In this paper, we propose a channel estimation method for 16-QAM or higher-order modulated signals without using pilot signal transmission using Sequential K-means Clustering (SKC). The existing channel estimation method using K-means clustering can be applied only to QPSK with a constant absolute value of 1. However, the conventional techniques have a problem in that they can not be applied to a 16QAM or higher-order modulation method in which the absolute value of a complex number representing a data symbol is not the same. On the other hand, the proposed channel estimation scheme using SKC provides a new center point method called reference center point and solves the problem in conventional K-means clustering-based channel estimation schemes. In order to verify the performance of the channel estimation scheme using the SKC proposed in this paper, the mean square error and the symbol error rate are used as performance metrics. Through the performance evaluation results, it is confirmed that the proposed channel estimation method using SKC and the reference center are successfully applied to the channel estimation using the higher order modulation signal of 16QAM or more. Even though the pilot signal is not used, the channel estimation method is superior to the least square channel estimator Respectively.
Keywords:
sequential K-means clustering, channel estimation, reference centerⅠ. 서 론
이동 통신 시스템에서 다중 경로에 대한 채널 추정은 신호를 검파하는 과정에서 필수적이다. 다중 경로 채널을 추정하기 위하여 기지국과 단말은 파일럿 신호(pilot signal)를 전송하게 된다. 그러나 파일럿 신호의 전송은 무선 자원을 추가로 소모하기 때문에 실질적인 데이터 전송률을 감소시킨다. 이러한 무선 자원의 비효율적 활용문제를 개선하기 위하여 파일럿 신호를 효율적으로 전송하기 위한 연구들이 진행되어왔다[1][2].
딥 러닝(Deep Learning)은 인공 지능분야 중 한 분야로써 컴퓨터 하드웨어의 발전으로 컴퓨터가 방대한 계산처리를 처리하게 됨으로써 연구가 활발히 진행되고 있다[3]. 최근에는 딥 러닝 기술을 무선 통신 분야에 적용시키고 있는데, 다중 안테나(MIMO, Multiple Input Multiple Output), 채널 추정, 신호 검파에 적용시킨 연구들이 발표 되었다[4][5]. 특히 딥 러닝 기술을 적용시킨 채널 추정 연구들 중에서 비지도 학습 알고리즘중 하나인 K-means 알고리즘을 채널 추정에 적용하여 파일럿 신호 전송 없이 채널을 추정하는 연구가 발표되었다[6].
기존의 K-means 군집화를 이용하여 파일럿 신호 없이 채널을 추정하는 채널 추정 기법(PCE, Pilotless Channel Estimator)들은 데이터 심볼의 군집으로부터 중심점을 도출하여 중심점의 크기(Amplitude)와 위상(Phase)을 검출함으로써 채널을 추정하였다. 도출된 군집 중심점들을 이용하여 채널의 영향을 받아 크기와 위상이 변화된 참조 심볼들을 추정한다[6][7]. 그러나 기존 PCE는 QPSK 데이터 심볼들에만 제한적으로 적용될 수 있다는 문제점이 있다. 16QAM 이상의 고차변조들은 QPSK와 다르게 성상도(Constellation)의 심볼들을 표현하는 복소수의 절댓값이 1이 아니며 변조 기법 별로 상이하다. 이러한 차이점 때문에 QPSK에서 사용하는 PCE는 고차변조된 신호들의 군집으로부터 중심점을 정확하게 계산하지 못한다. 현대의 이동통신 시스템에서는 16QAM 내지 256QAM의 고차변조를 사용하고 있기 때문에 고차변조 신호를 이용하여 파일럿 신호 없이 채널을 추정하는 기법에 대한 연구가 필요하다.
본 논문에서는 16QAM 이상의 고차변조에 적용할 수 있는 파일럿 신호를 사용하지 않는 채널 추정기법을 제안하였다. 제안하는 채널 추정기법은 순차적 K-Means 군집화(SKC, Sequential K-means Clustering)를 이용하여 군집 중심점을 도출한다. SKC는 입력된 데이터 심볼들을 단계별로 4개의 부분 군집들로 분할한다. SKC에 의하여 도출되는 군집 중심점들에 새로 제안된 변조 기법별 참조 중심점(Reference Center)을 적용하여 최종적으로 채널을 추정하게 된다. 본 논문에서 제안하는 SKC를 이용한 채널 추정기법(SKC-PCE)의 추정성능을 검증하기 위하여 평균 제곱 오차(MSE, Mean Squared Error)와 심볼 오류율(SER, Symbol Error Rate) 측정 실험을 통하여 채널추정 성능을 검증하였다.
Ⅱ. 시스템 모델
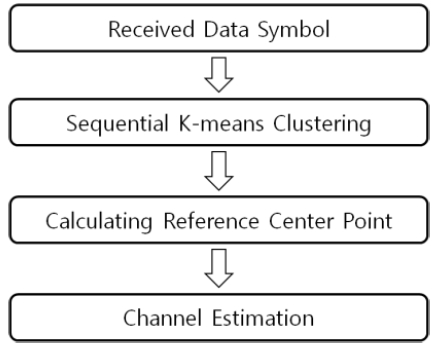
그림 1에는 본 논문에서 SKC-PCE를 이용한 채널 추정 시스템 블록도가 도시되어 있다. SKC-PCE는 파일럿 신호 전송 없이 수신 심볼들만 이용하여 채널을 추정한다. 수신기로 수신되는 심볼들을 복수개의 군집으로 군집화하여 각 군집들의 군집 중심점들을 추정하게 된다. 기존의 PCE 연구는 QPSK 신호만을 대상으로 하였으므로 전송 신호의 절댓값의 크기가 1로 일정하다고 가정하고 4개의 군집에 대한 중심점을 직접 추정하였던 반면[6][7], SKC-PCE는 M-ary 신호에 대해서 최초 4개의 군집을 형성하고 각각의 군집에 대해서 4개의 군집을 형성하는 동작을 log4M회 반복하며 각각의 군집화에 대한 중심점을 형성한다. SKC-PCE에서 참조 중심점을 설정하는 두 가지 방식을 제시하고 있으며 자세한 내용은 3장에서 다루기로 한다.
직교 주파수 분할 다중 방식(OFDM, Oorthogonal Frequency-Division Multiplexing) 전송에서 하나의 상관 시간(Coherence Time)과 상관 주파수(Coherence Frequency)내에서 수신기로 수신되는 N개의 수신신호는 다음과 같이 표현될 수 있다[7].
| (1) |
식 (1)에서 xm는 송신되는 M-ary 심볼을 의미한다. M ∈ {4,16,64,256}이며 각각 QSPK, 16QAM, 64QAM, 256QAM에 대응되며, 현재 구현되어 있거나 개발이 진행 중인 4세대와 5세대 이동통신 시스템에서 사용되고 있는 변조 기법들이다[8]. m은 수신 심볼에 대한 색인을 의미하며, h는 N(0,σ)인 복소-가우시안(Complex-Gaussian) 분포를 따르는 랜덤변수이다. n은 백색잡음(Additive White Gaussian Noise)으로써 평균값이 0이고 표준편차가 N0인 복소 가우시안 확률 분포를 따르는 랜덤 변수이다.
Ⅲ. 채널 추정 방법
일반적인 K-Means 알고리즘은 다음과 같이 군집화 과정의 반복 수행함으로써 구분되어 있지 않은 N개의 데이터를 K개의 군집으로 분할한다. 1) N개의 데이터 중 임의로 K(N> K)개의 중심점을 선택하고, 2) 입력된 데이터들은 모든 중심점과의 유클리드 거리(Euclidean distance)를 계산하여 거리가 가장 가까운 중심점을 선택한다. 3) 동일 중심점을 선택한 데이터들의 집합을 하나의 군집으로 정의하며, 하나의 군집에 포함된 데이터들의 산술 평균을 통하여 새로운 군집 중심점을 도출한다. 새로 계산된 K개의 중심점을 이용하여 1), 2), 3)을 사전에 정해진 L회만큼 반복하여 최종 K개의 군집과 각 군집 별 중심점이 결정된다[9][10].
일반적인 K-Means 군집화라면 채널 추정을 위해서 M-ary 신호에 대해서 M개의 군집을 형성하고 각각의 군집에 대한 중심점을 도출하여야 한다. 반면 SKC는 데이터 심볼의 변조 방식과 상관없이, 전체 수신 심볼에 대해서 최초 4개의 군집을 형성한다. 하나의 군집에 포함되어 있는 데이터 심볼의 집합을 Sl ∈ {1,2,3,4}이라 할 때, 각 군집의 추정된 중심점들은 군집에 포함된 심볼들을 이용하여 다음과 같이 계산될 수 있다.
| (2) |
식 (2)에서 E[x]는 집합 x에 포함되는 모든 원소에 대한 산술 평균을 의미한다.
3.1 First-Step 채널 추정 방법
첫 번째 채널 추정 방법은 식 (2)의 결과를 직접 활용하여 채널의 크기와 위상을 구한다. 이 때 송신된 심볼의 변조 방식에 따라서 평균 심볼의 크기가 상이하므로, 변조 방식에 따른 평균 심볼의 크기를 참조중심점으로 정의하며 아래와 같이 계산된다.
| (3) |
식 (2)에서 αM = E[|xm|], m = 1,...,M 이다.
식 (1)의 채널 h를 크기 A와 위상 θ으로 표현하면 다음과 같이 표현할 수 있다.
| (5) |
군집화 알고리즘의 식 (1)에서 백색잡음의 효과가 상대적으로 적다고 가정하였을 때, 은 채널에 의하여 크기와 위상이 변화된 참조중심점 값과 유사한 값을 가지게 된다.
| (6) |
을 다음과 같이 계산하여 채널의 크기와 위상에 대한 정보를 얻을 수 있다.
| (7) |
식 (7)에서 실수 영역은 채널의 크기에 대한 정보를 가지고 있고, 허수 영역은 채널의 위상에 대한 정보를 가지게 된다. 따라서 다음과 같은 연산을 통하여 채널의 크기와 위상을 추정할 수 있다.
| (8) |
식 (8)에서 real[x] 연산은 x의 실수 영역을 의미하며 imag[x]연산은 x의 허수 영역을 의미한다. 채널 추정 과정에서와 달리 최종 추정된 채널의 크기와 위상은 송신 심볼이 사용하고 있는 변조 방식에 따라 달라지는 것이 아니므로 최종 결과에서 첨자 M이 제거된 채널의 와 가 도출되었다.
3.2 Final-Step 채널 추정 방법
First step 채널 추정 방법은 송신하는 심볼의 변조 기법을 고려하지 않고 4개의 군집으로만 분할하여 중심점을 도출하여 채널 추정을 하였다. 본 논문에서 다루고 있는 QPSK 내지 256QAM은 M 종류의 심볼을 전송함에 있어 성상도 상 하나의 사분면에 M/4개의 심볼을 전송하고 있다. 따라서 각 사 분면에 존재하는 M/4개의 심볼에 대한 수신신호를 하나의 군집으로 보고 식 (2)에서 중심점을 도출한 것이다. 그러나 실제 전송된 심볼별 군집화를 수행한 것이 아니므로, 채널 추정 결과가 부정확할 수 있다.
Final step 채널 추정 방법은 M 종류의 심볼을 가지고 있는 수신 신호에 대해서 SKC를 사용하여 M개의 군집을 형성한다[11]. 최종 단계까지 M개의 군집에 대한 중심점을 추정한 것에 기반하여 채널을 추정하므로 final step이라고 명명하였다. 식 (2)에서 최초 4개의 군집이 형성된 이후 각 군집 별로 M/4개의 군집을 만들어 최종 중심점을 다음과 같이 구한다.
| (9) |
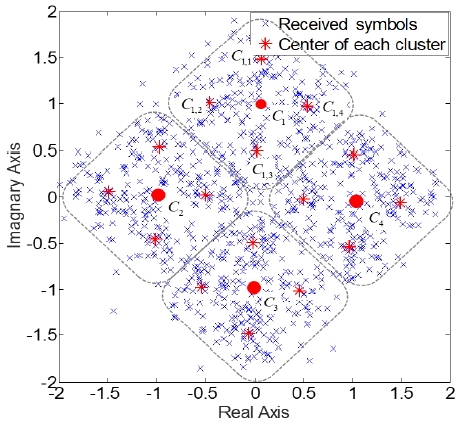
그림 2에 식 (2)를 사용한 군집화 결과 및 중심점 추정 결과가 도시되어 있다. 수신된 16QAM 심볼들은 점선으로 표시된 4개의 군집으로 분할되며, SKC에 따라서 각각의 군집은 4(M(=16)/4) 개의 군집으로 분할된다. 최종 단계에서 C1은 식 (2)와 같이 C1,1, C1,2, C1,3, C1,4의 산술 평균에 의해서 구할 수 있다. 그림 2는 16QAM에 대한 예를 들고 있으나, 64QAM과 256QAM에도 동일한 방법을 적용하여 중심점 추정이 가능하다.
Ⅳ. 신호별 채널 추정 성능 평가 및 분석
SKC-PCE의 성능을 평가하기 위하여 16QAM과 64QAM으로 전송된 데이터 심볼들을 이용하여 채널을 추정하였다. 식 (2)를 사용한 경우 first step으로 표시하였고, 식 (9)를 사용하는 경우 final step으로 표시하였다. 우선, 고차 변조된 데이터 심볼을 이용한 채널 추정에 필수적으로 사용되는 참조 중심점 추정 성능을 검증하기 위하여 와 채널이 반영된 Cl의 MSE를 측정하였다. 참조 중심점 추정성능을 검증하기 위한 MSE 식은 아래와 같이 표현될 수 있다.
| (10) |
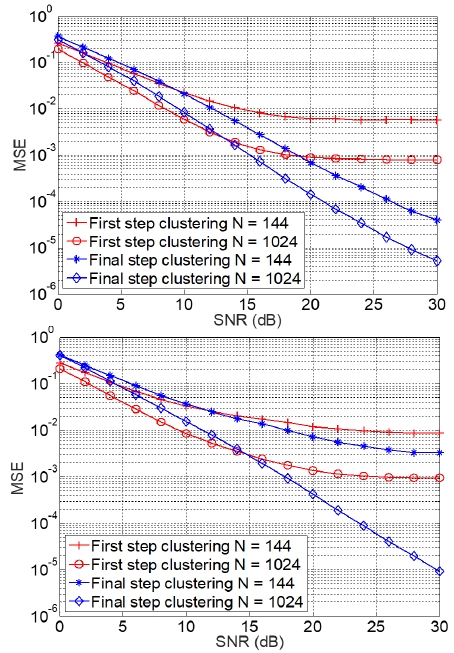
그림 3에는 수신 심볼 수와 first step과 final step에 의한 참조 중심점 추정 방법에 따른 참조 중심점 MSE 결과가 도시되어 있다. 그림 3의 위쪽 그래프는 16QAM에 대한 MSE 결과이며, 아래쪽 그래프는 64QAM에 대한 MSE 결과이다.
그림 3을 살펴보면 수신 심볼의 수가 증가하면 참조 중심점 추정성능이 개선됨을 확인할 수 있다. 이것은 K-Means 군집화의 기본적인 특징으로 채널 추정에 사용된 심볼 수 144는 LTE와 5G NR 시스템에서 하나의 단말에 전송할 수 있는 최솟값이며 성능 측면에서 보면 최저 성능을 의미한다. 심볼 수 1024는 실험적으로 채널 추정에 사용하는 심볼의 수를 증가시켜도 식 (10)의 MSE가 개선되는 정도가 관찰되기 힘든 심볼 수를 의미한다.
그림 3에서 관찰되는 흥미로운 결과는, first step 추정 기법이 final step 추정 기법보다 SNR 0~14dB 영역에서 더 우수한 MSE 성능을 보이고 있지만, 특정 SNR값(16~20dB) 이후로 더 이상 성능이 개선되지 않은 다는 것이다. 반면 final step 추정 기법은 SNR이 낮은 영역에서 first step 추정 기법 대비 MSE 성능이 낮지만, SNR이 증가하면 채널이 반영된 참조 중심점과 실체 추정된 중심점 사이의 오차가 매우 빠른 속도로 감소하게 된다. 이러한 현상이 발생하는 이유는, SNR이 낮은 영역에서 중심점 추정 과정에 평균(averaging) 연산에 의한 노이즈 감소(noise reduction) 효과를 얻기 위하여 더 많은 수의 심볼이 필요한데, first step 추정 기법은 4개의 군집만을 사용하므로 단위 군집 당 포함되는 심볼 수가 final step 추정 기법 대비 더 많기 때문이다. 평균 연산에 의한 노이즈 감소 기법은 신호처리에서 일반적으로 활용된다[12]. 반대로 SNR이 증가하는 경우 동일한 MSE를 달성하기 위하여 필요한 심볼 수가 감소하게 되므로, 군집별 심볼 수가 적어도 군집의 중심점을 정확히 추정할 수 있다.
Final step은 M개의 중심점을 모두 추정한 후 정보를 종합하여 최종 중심점을 추정하게 되므로 final step 추정 기법의 MSE가 first step의 MSE 대비 적은 값을 가지게 된다.
을 이용하여 정상적으로 채널을 추정하였는지 검증하기 위하여 식 (8)에 의해서 구성되는 와 h의 MSE를 측정하였다. 그림 4의 첫 번째 그래프는 16QAM에 대한 채널추정 성능 결과이며 두 번째 그래프는 64QAM에 대한 채널추정 성능 결과이다. 그림 4를 보면 채널 추정 성능이 그림 3의 결과와 동일하게 수신 심볼의 수에 비례하여 개선됨을 확인할 수 있다.
이는 참조 중심점 추정성능이 식 (6)과 같이 채널 추정에 직접적인 영향을 주기 때문이다. 또한 그림 3의 결과와 마찬가지로 SNR 0~16dB 영역에서 첫 번째 추정 방법이 두 번째 추정 방법보다 우수한 성능을 나타내고 있음을 확인할 수 있다. First step 추정 기법은 SNR 16dB 이상의 영역에서 더 이상 성능이 개선되지 않은 현상을 보이고 있으나, final step 추정 기법의 성능은 SNR 값이 증가할수록 추정 성능 또한 개선되고 있음을 확인할 수 있다.
그림 3에서 군집의 중심점에 대한 추정 성능 결과와 그림 4의 실제 채널 추정 성능 결과의 경향성이 일치함을 확인함으로써 제안한 참조 중심점 값을 적용하는 것이 채널 추정의 성능에 직접적인 영향을 주고 있음을 확인할 수 있다. 또한 충분한 심볼 수가 확보되지 않은 경우 SNR이 높은 영역에서 First step을 사용한 경우 LS 채널 추정기와 성능 역전이 나타나게 되므로 통신 시스템의 동작 SNR 영역을 고려하여 채널추정기를 선택해야 함을 알 수 있다.
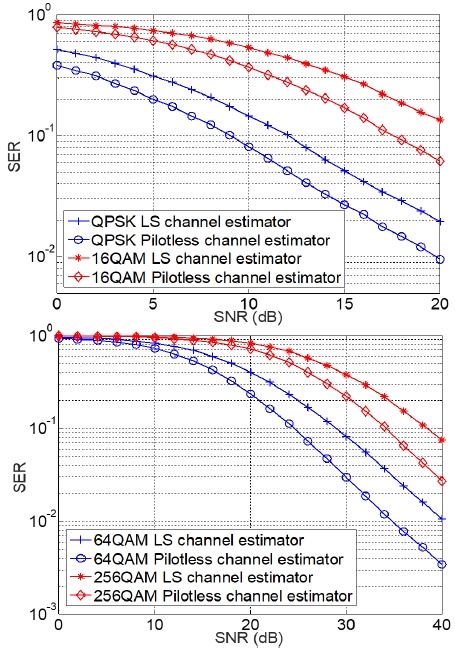
두 가지 실험 결과를 통하여 채널 추정 성능을 검증하였지만, 수신 신호가 정상적으로 검파가 되었는지 검증할 필요가 있다고 판단하여 실험을 통하여 SER결과를 그림 5에 도시하였다. SKC-PCE는 final step 방식을 적용하였으며 비교를 위하여 최소제곱(LS, Least Square) 채널 추정기를 사용하였다. LS 채널 추정기는 파일럿 신호를 사용하는 채널 추정 기법 중 가장 일반적으로 사용된다. LS 채널 추정기의 MSE 성능은 1/SNR로 알려져 있으며 그림 4의 MSE 성능과 비교해 보면 SKC-PCE가 LS 채널 추정기 대비 MSE 측면에서 우수한 성능을 보여주고 있음을 확인할 수 있다.
정확한 채널 추정의 결과로 그림 5의 SER 결과에서도 SKC-PCE는 QPSK 내지 256QAM까지 모든 변조기법에서 LS 채널 추정기 대비 우수한 성능을 보여 준다.
SKC-PCE를 사용한 채널 추정 성능을 평가한 결과에 기반하여 기존의 채널 추정 기법과의 비교 분석을 표 1에 요약하여 제시하였다. 기존의 PCE 대비 SKC-PCE에서 개선된 점은 SKC-PCE를 사용하면 16QAM 이상의 고차 변조 기법에 대한 채널 추정이 가능하다는 것이다. QPSK의 경우 기존 PCE와 차이가 없기 때문에 성능이 동일하다. 파일럿 신호를 사용하는 LS 기법과 MSE를 비교해 보면, 그림 4의 결과에서 확인할 수 있는 바와 같이 SKC-PCE의 final step 기법이 SNR 0~ 30dB 범위에서 LS 채널 추정기 대비 우수하다. 또한 1024개 이상의 충분한 수의 데이터 심볼이 확보된 경우 모든 변조 기법에 대해서 SKC-PCE가 LS 채널 추정기 대비 MSE 성능이 우수한 것을 확인할 수 있다.
V. 결 론
본 논문에서는 QPSK부터 256QAM까지의 변조 기법에 대하여 SKC 및 참조 중심점을 이용하여 파일럿 신호 없이 채널을 추정하는 기법을 제안하였다. 참조 중심점 추정과정에서 first step과 final step두 가지 참조 중심점 추정방법을 제시하고 MSE와 SER을 측정하여 참조 중심점 추정방법에 따라 채널추정 성능을 비교하였다. 채널추정 정확도에 있어서 first step 채널 추정 기법이 SNR이 낮은 영역에서final step 채널 추정 기법보다 우수한 성능을 나타내고 있으나, SNR이 높은 영역에서는 성능이 더 이상 개선되지 않았다. 그러나 final step 채널 추정 기법은 first step 채널 추정 기법과 달리 SNR 값이 증가할수록 추정 성능 또한 개선됨을 확인할 수 있었다. 특히MSE와 SER을 통한 성능 평가를 통하여 LS 채널 추정기법과 비교하였을 때 제안한 채널 추정 기법이 개선된 채널추정 성능을 가지고 있음을 확인할 수 있었다.
Acknowledgments
이 논문은 2019년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2018R1D1A1B07050143)
References
-
H. Xu, N. Huang, Z. Yang, J. Shi, B. Wu, and M. Chen, "Pilot Allocation and Power Control in D2D Underlay Massive MIMO Systems", IEEE Communications Letters, 21(1), p213-216, Jan.), (2017.
[https://doi.org/10.1109/lcomm.2016.2597236]

-
X. Wei, S. Fan, Y. Xiao, Q. You, and W. Chen, "Space Shift Keying MIMO Transmission with Reduced Pilot Overhead", IEEE 8th Annual Computing and Communication Workshop and Conference, p1-5, Jan.), (2018.
[https://doi.org/10.1109/ccwc.2018.8301730]

- D. Jeong, "Trend on Artificial Intelligence Technology and Its Related Industry", Korea Institute of Information Technology Magazine, 15(2), p21-28, Dec.), (2017.
-
N. Samuel, T. Diskin, and A. Wiesel, "Deep MIMO detection", arXiv preprint arXiv:1706.01151 (2017).
[https://doi.org/10.1109/spawc.2017.8227772]

-
H. Ye, G. Y. Li, and B. H Juang, "Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems", IEEE Wireless Communications Letters, 7(1), p114-117, Jan.), (2018.
[https://doi.org/10.1109/lwc.2017.2757490]

-
K. Jung, and H. Wang, "Pilotless Channel Estimation Scheme using Clustering-based Unsupervised Learning", International Symposium on Wireless Communication Systems, p1-5, Aug.), (2018.
[https://doi.org/10.1109/iswcs.2018.8491198]

- H. Wang, "Performance Evaluation of Pilotless Channel Estimation with Limited Number of Data Symbols in Frequency Selective Channel", International Journal of Contents, 14(2), p1-6, Jun.), (2018.
- E. Dahlman, and S. Parkvall, "4G, LTE-Advanced Pro and The Road to 5G", 3rd Ed., Academix Press, (2016).
- B. Sklar, "Digital Communications: Fundamentals and Applications", 2nd Ed., PrenticeHall, (2001).
- K. Alsabti, S. Ranka, and V. Singh, "An Efficient k-means Clustering Algorithm", Proc. First Workshop High Performance Data Mining, p1-5, Mar.), (1998.
-
K. Jung, and H. Wang, "Higher-order Modulation Signal Detection Scheme Using Sequential Clustering", Journal of Korean Institute of Information Technology, 17(3), p87-93, Mar.), (2019.
[https://doi.org/10.14801/jkiit.2019.17.3.87]

- Y. Lee, H. Kim, S. Park, and S. Lee, "Noise reduction for channel estimation based on pilot-block averaging in DVB-T receivers", IEEE Transactions on Consumer Electronics, 52(1), p51-58, Feb.), (2006.

2004년 2월 : 연세대학교 전기전자공학과(공학사)
2010년 8월 : 연세대학교 전기전자공학과(공학박사)
2012년 3월 ~ 현재 : 상명대학교 정보통신공학과 조교수
관심분야 : 이중편파안테나, 머신러닝, 군집화알고리즘