CFAR와 합성곱 신경망을 이용한 기두부와 단 분리 시 조각 구분

Ⅰ. 서 론

초고속 고기동을 하는 미사일은 위협적인 무기 체계 중 하나로써 이에 대한 방어체계 시스템을 구축하는 것은 매우 중요한 문제이다. 초고속 고기동 미사일에 대한 방어체계 시스템을 구축하기 위해서는 비행 도중 발생하는 단 분리 시 조각과 기두부가 구분이 되어야 한다.

기두부와 단 분리 시 조각은 비행 도중 서로 다른 미세 운동을 하며 이러한 미세 운동은 레이더를 통해 측정이 가능하다[1][2]. 기두부의 경우 자세 제어를 위해 장동(Nutation) 운동을 하며, 단 분리 시 조각의 경우 별도의 자세 제어를 하지 않으므로 텀블링(Tumbling) 운동을 한다. 이와 같이 기두부와 단 분리 시 조각의 서로 다른 미세 운동에 의해 미세 도플러 주파수가 다르게 나타나며, 이를 이용하여 탄두와 기만체 또는 단 분리 시 조각을 구분하는 연구가 진행되고 있다.

탄두와 기만체를 구분한 연구로는 탄두와 기만체의 중량 차이에 발생하는 미세 도플러 signature의 진폭 차이를 통해 탄도미사일과 기만체를 구분한 연구[3], IRT(Inverse Radon Transform)와 pseudo-Zernike moments를 통해 탄두와 기만체를 구분한 연구[4], TFD(Time-Frequency Distribution)와 HRRP(High Resolution Range Profile) serial를 이용하여 탄두와 기만체를 구분한 연구가 있다[5].

탄두와 단 분리 시 조각을 구분한 연구로는 동적 RCS의 주기성과 통계적 특성을 이용하여 기두부와 단 분리 시 조각을 구분한 연구가 있다[6].

이러한 기존의 연구들은 탄두의 미세 운동을 세차(Precession) 운동을 한다고 가정하여 구분을 하였다. 그러나 실제 탄두의 경우, 세차 운동이 아닌 장동 운동을 하므로 실제 탄두의 미세 운동이 고려되어지지 않았다. 또한, 탄두와 기만체 또는 단 분리 시 조각을 구분하기 위해 특성 벡터를 직접 추출하는 복잡한 과정을 거친다.

참고문헌 [7]에서는 탄두의 장동 운동을 모델링하여 CVD(Cadence Velocity Diagram)를 획득한 후, 이를 통해 특성 벡터를 추출하여 탄두와 기만체를 구분한 연구가 있다. 그러나 참고문헌 [7] 역시 특성 벡터를 직접 추출하므로 복잡한 과정을 거친다.

합성곱 신경망은(CNN, Convolutional Neural Networks) 입력 데이터를 영상으로 받으며, 입력 영상으로부터 자체적으로 표적의 특성을 추출하여 구분하므로, 특성 벡터를 직접 추출하는 과정을 생략해도 되는 장점이 있다. 또한, 최근에는 다양한 합성곱 신경망 모델들이 소개되고 있으며, 모두 뛰어난 구분성능을 보이고 있다[8]-[10]. 현재 합성곱 신경망은 음성 인식, 얼굴 인식 등 다양한 분야에 적용되고 있으며, 합성곱 신경망을 이용하여 기두부와 단 분리 시 조각을 구분한 연구가 있다[11]-[13]. 그러나 참고문헌 [13]은 기두부의 미세 운동을 단순화하기 위해 세차 운동을 한다고 가정하여 구분 연구를 하였다.

본 논문에서는 장동 운동을 하는 기두부와, 텀블링 운동을 하는 단 분리 시 조각을 합성곱 신경망을 이용해 구분하였다. 합성곱 신경망에 사용 된 입력 영상으로는 미세 도플러 스펙트로그램을 사용하였다. 또한 구분 성능을 향상시키기 위해, 미세 도플러 스펙트로그램에 CA-CFAR(Cell Averaging-Constant False Alarm Rate)를 사용하여 전처리 과정을 수행하였다.

시뮬레이션 결과 전처리 과정을 수행한 미세 도플러 스펙트로그램을 합성곱 신경망의 입력 영상으로 사용하였을 경우, 전처리 과정을 수행하지 않은 미세 도플러 스펙트로그램보다 모든 SNR환경에서 뛰어난 구분성능을 보였다.

Ⅱ. 관련 이론

2.1 CA-CFAR

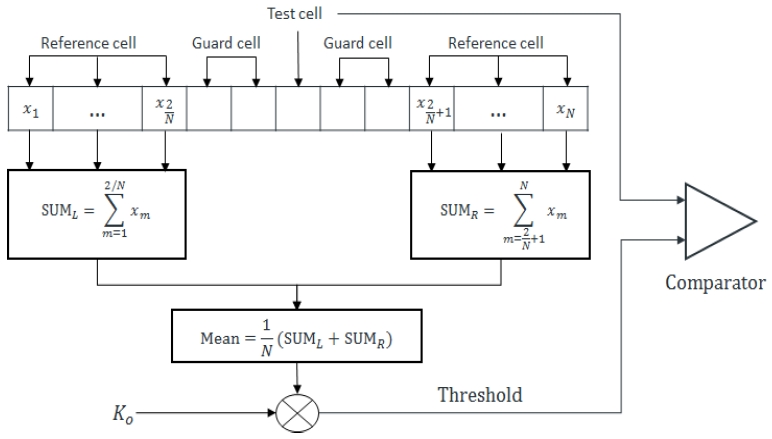
표적은 레이더에서 수신된 신호가 임의의 임계값을 넘으면 탐지가 된다. 그러나 잡음이 클 경우, 잡음 또한 임계값을 넘어가는 현상이 발생하여 오경보(False-alarm)가 발생한다. CFAR는 임계값을 잡음환경에 따라 자동적으로 변화시켜주어 오경보율을 일정하게 만들어준다. CFAR는 다양한 형태로 존재하지만 본 논문에서는 가장 기본적인 CA-CFAR를 사용하였다. CA-CFAR 구조는 그림 1과 같다[14].

Fig. 1.

CA-CFAR structure

그림 1에서 기준 셀(reference cell)은 테스트 셀(test cell)의 출력하기 위한 셀이며, 보호 셀(guard cell)은 테스트 셀 주변의 셀로 테스트 셀의 출력을 구할 때 무시되어지는 셀이다. 테스트 셀은 임계값과 비교하여 임계값보다 클 경우 표적으로 간주되어 진다. 임계값은 기준 셀들의 평균값과 K₀의 곱에 의해 결정된다. 따라서 임계값은 잡음에 따라 변하므로 오경보율을 일정하게 만들어 준다[14].

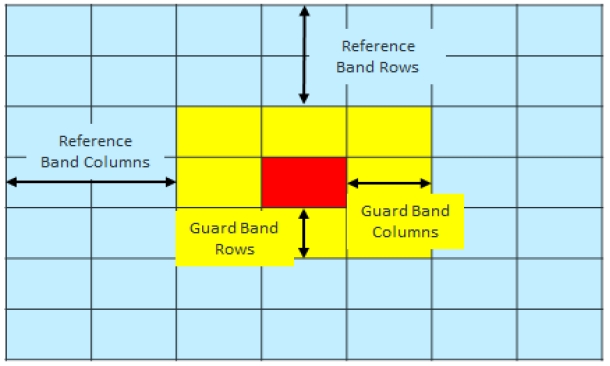
CA-CFAR는 기준 셀의 개수가 많은 수록 잡음에 강건하지만 계산 시간이 오래 걸린다. 또한 기준 셀 안에 다른 표적이 존재할 경우, 평균값이 높아지기 때문에 탐지확률을 감쇄시킨다. 보호 셀의 경우, 표적에 대한 정보가 여러 셀에 존재할 수 있기 때문에 이에 맞게 보호 셀의 개수를 설정해 주어야 한다. 그러나 본 논문에서는 2차원 데이터인 스펙트로그램에 CA-CFAR를 적용한다. 따라서 기준 셀과 보호 셀의 범위를 그림 2와 같이 행과 열로 설정해 주어야 한다[15].

Fig. 2.

Two-dimensional CA-CFAR

2.2 합성곱 신경망

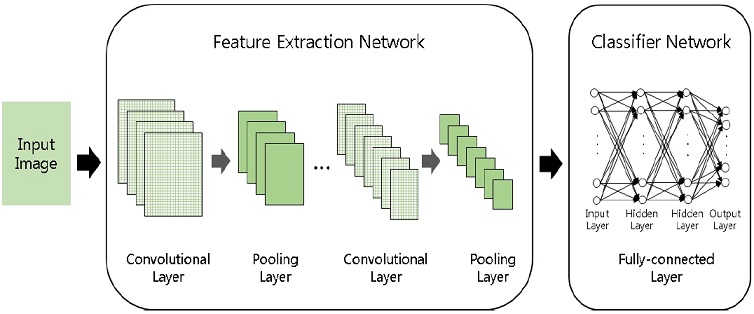
합성곱 신경망은 그림 3과 같이 표적의 특성을 추출하는 컨벌루셔널 계층(convolutional-layer), 풀링 계층(pooling-layer)과 표적을 구분하는 완전 연결된 계층(fully-connected layer)로 구분할 수 있다[13][16].

Fig. 3.

CNN structure

컨벌루셔널 계층에서는 필터를 입력영상의 좌측 상단부터 적용하여 컨벌루션 연산을 통해 표적의 특성을 추출해 내며, 이를 피쳐맵(feature map)이라고 한다. 이 때 추출 된 피쳐맵은 입력 영상보다 작아지게 된다. 따라서 이를 보완하기 위해 입력 영상 양쪽 끝에 0을 추가하는 제로 패딩(zero-padding) 기법을 사용한다[16].

풀링 계층에서는 추출 된 피쳐맵의 크기를 감소시킨다. 피쳐맵의 크기를 감소시키는 방법으로는 최댓값 풀링(Max-pooling)과 평균 풀링(Mean-pooling)이 있다. 최댓값 풀링은 패치 내의 값 중 가장 큰 값을 선택하는 방법이며, 평균 풀링은 패치 내의 평균 값을 나타내는 방법이다[13].

풀링 계층을 통해 피쳐맵의 크기를 감소시킨 후, 완전 연결 된 계층을 통해 표적을 구분한다. 완전 연결 된 계층은 여러 개의 은닉층으로 구성되어 있으며, 출력층에서는 soft-max함수를 통해 표적을 구분한다.

Ⅲ. 미세 운동 모델링

기두부는 비행 도중 중력, 항력, 양력, 공기 저항 등 다양한 힘을 받기 때문에, 안정적인 운동 상태를 유지할 수 없다. 따라서 안정적인 운동 상태를 유지하기 위해 장동 운동을 한다. 본 논문에서 장동 운동은 회전(Spinning) 운동, 원추(Coning) 운동, 진동(Oscillating) 운동을 모두 하는 운동을 의미한다[17].

반면에, 단 분리 시 조각은 안정적인 운동 상태를 유지하기 위한 별도의 운동을 하지 않는다. 따라서 공기 저항에 의해 뒤쪽으로 전복되는 현상이 발생하며 이를 텀블링 운동이라 한다[17]. 본 논문에서는 기두부와 단 분리 시 조각의 미세 도플러 스펙트로그램을 획득하기 위해 장동 운동과 텀블링 운동을 모델링하였다.

3.1 장동 운동 모델링

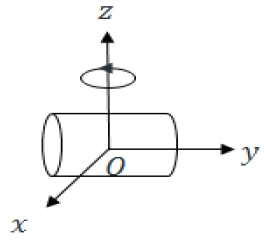
장동 운동을 모델링하기 위해, 표적이 3차원 좌표 공간에 있다고 가정한다. 이 때 표적의 회전축은 z방향과 일치해야 하며, 표적의 무게 중심은 원점에 위치해야 한다. 3차원 좌표 공간에 존재하는 표적은 식 (1)과 같이 N개의 메쉬(Mesh)로 나타 낼 수 있다[6].

$\[ M=\left[P_1,P_2,\cdots ,P_n,\cdots ,P_N\right] \]$

(1)

여기서, P_n은 n번째 메쉬를 나타내며 P_n은 식 (2)와 같이 나타낼 수 있다.

$\[ P_n=\left[\overrightarrow{V_1},\overrightarrow{V_2},\overrightarrow{V_3}\right] \]$

(2)

$$ \overrightarrow{V_i}$$는 메쉬를 이루고 있는 점의 좌표로 식 (3)과 같이 나타 낼 수 있다.

$\[ \overrightarrow{V_i}={\left[v_x^i,v_y^i,v_z^i\right]}^T \]$

(3)

N개의 메쉬로 이루어진 표적이 장동 운동을 하면, 장동 운동을 하는 메쉬들의 위치는 식 (4)와 같이 나타 낼 수 있다.

$\[ M_N=TM \]$

(4)

여기서 T는 장동 운동 회전 행렬로 식 (5)와 같이 나타낸다.

$\[ T=R_c{P}_c{R}_o{P}_o{R}_s \]$

(5)

여기서 R_s는 회전 운동의 회전 행렬, P_o는 진동 운동의 기울임 행렬, R_o는 진동 운동의 회전 행렬, P_c는 원추 운동의 기울임 행렬, R_c는 원추 운동의 회전 행렬로 식 (6)과 같다.

$\[ \begin{array}{c}{R}_s=\left[\begin{array}{ccc}\cos 2\pi f_s\hfill & -\sin 2\pi f_s& 0\\ \sin 2\pi f_s& \cos 2\pi f_s& 0\\ 0& 0& 1\end{array}\right]\hfill \\ P_o=\left[\begin{array}{ccc}\cos \beta \hfill & 0& \sin \beta \\ 0& 1& 0\\ -\sin \beta & 0& \cos \beta \end{array}\right]\hfill \\ R_o=\left[\begin{array}{ccc}\cos 2\pi f_o\hfill & -\sin 2\pi f_o& 0\\ \sin 2\pi f_o& \cos 2\pi f_o& 0\\ 0& 0& 1\end{array}\right]\\ \begin{array}{c}{P}_c=\left[\begin{array}{ccc}\cos \alpha \hfill & 0& \sin \alpha \\ 0& 1& 0\\ -\sin \alpha & 0& \cos \alpha \end{array}\right]\hfill \\ R_c=\left[\begin{array}{ccc}\cos 2\pi f_c\hfill & -\sin 2\pi f_c& 0\\ \sin 2\pi f_c& \cos 2\pi f_c& 0\\ 0& 0& 1\end{array}\right]\end{array}\end{array} \]$

(6)

여기서 f_s는 회전 운동의 초당 회전 수, f_o는 진동 운동의 초당 회전 수, f_c는 원추 운동의 초당 회전 수, α는 원추 운동의 기울임 각, β는 진동 운동의 기울임 각이다. 그림 4는 장동 운동을 하는 기두부이다.

Fig. 4.

Nutation motion of warhead

그러나 식 (4)를 통해 장동 운동하는 기두부의 동적 RCS를 계산할 경우, 실시간으로 메쉬의 좌표를 변경 시켜가며 계산해야 하기 때문에 많은 계산시간이 소모된다. 따라서 표적을 고정 시키고, 안테나의 위치를 변화시켜 동적 RCS를 계산하였다. 안테나의 위치는 장동 운동 회전 행렬의 역행렬과, 안테나의 초기 위치 $$ \widehat{z}$$과 곱하여 나타낼 수 있으며, 식 (7)과 같다.

$\[ {AL}_N=T^{-1}\widehat{z} \]$

(7)

3.2 텀블링 운동 모델링

텀블링 운동을 모델링하기 위해, 마찬가지로 표적이 3차원 좌표 공간에 있다고 가정한다. 이 때 표적의 회전축은 z방향과 일치해야 하며, 표적의 무게 중심은 원점에 위치해야 한다. 3차원 좌표 공간에 N개의 메쉬로 이루어진 표적이 텀블링 운동을 하게 될 경우, 표적의 메쉬는 식 (8)과 같다[6].

$\[ M_T=R_{t}M \]$

(8)

여기서 R_t는 텀블링 운동의 회전 행렬로 식 (9)와 같다.

$\[ R_t=\left[\begin{array}{ccc}\cos 2\pi f_t\hfill & -\sin 2\pi f_t& 0\\ \sin 2\pi f_t& \cos 2\pi f_t& 0\\ 0& 0& 1\end{array}\right] \]$

(9)

여기서 f_t는 텀블링 운동의 초당 회전 수 이다. 마찬가지로, 식 (8)를 통해 텀블링 운동을 하는 단 분리 시 조각의 동적 RCS를 계산 할 경우, 실시간으로 메쉬의 좌표를 변경 시켜가며 계산해야 하기 때문에 많은 계산시간이 소모된다. 따라서 단 분리 시 조각 또한, 식 (10)과 같이 텀블링 회전 행렬 R_t의 역행렬과 안테나의 초기 위치 $$ \widehat{z}$$를 곱하여 안테나의 위치를 계산한 후, 단 분리 시 조각의 동적 RCS를 계산하였다. 그림 5는 단 분리 시 조각의 텀블링 운동이다.

$\[ {AL}_T=R_t^{-1}\widehat{z} \]$

(10)

Fig. 5.

Tumbling motion of debris

Ⅳ. 제안하는 방법

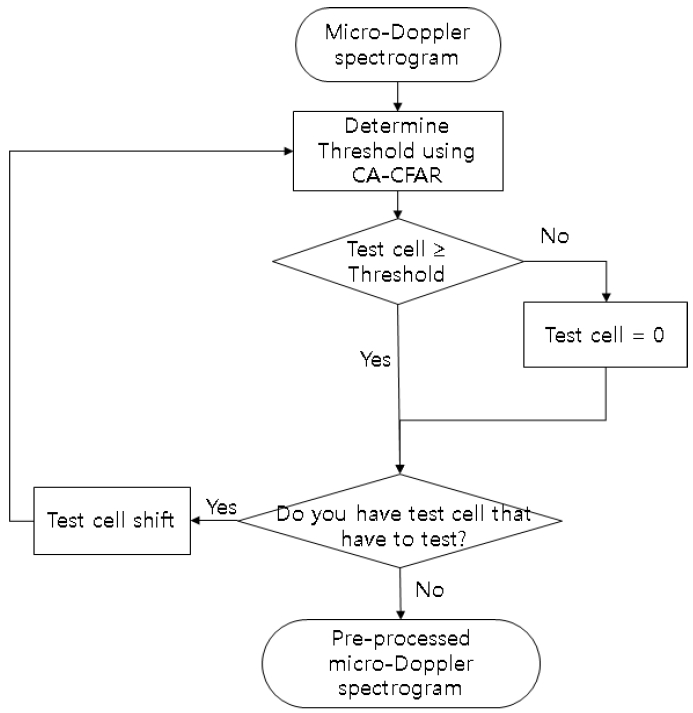
본 논문에서는 기두부와 단 분리 시 조각을 구분하기 위해 합성곱 신경망을 사용하였다. 합성곱 신경망의 입력 영상으로는 미세 도플러 스펙트로그램을 사용하였다. 획득한 미세 도플러 스펙트로그램은 CA-CFAR를 통해 전처리 과정을 수행하였다. 이 때 테스트 셀의 값이 임계값보다 클 경우, 테스트 셀의 값을 그대로 유지하였으며, 테스트 셀의 값이 임계값보다 작을 경우 테스트 셀의 값을 0으로 설정하였다.

이 때, 전처리 과정을 통해 획득한 미세 도플러 스펙트로그램은 RGB 영상이며, 영상 크기 또한 크다. 본 논문에서는 계산량을 줄이기 위해, 미세도플러 스펙트로그램을 그레이 스케일로 변화하였으며, 영상의 크기 또한 64×64로 감소시켰다.

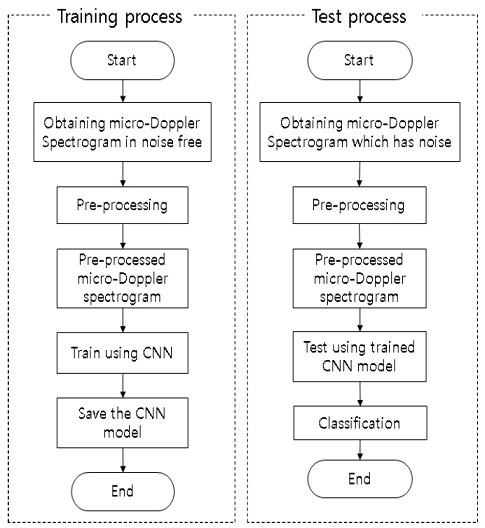
합성곱 신경망의 경우 학습 데이터의 양이 많을수록 구분 성능이 향상된다. 또한 표적의 초기 위상에 따라 획득하는 미세 도플러 스펙트로그램 다르므로, 본 논문에서는 표적의 초기 위상을 고려하여 학습 데이터의 양을 증가 시켰다. 이 때, 학습 데이터는 잡음이 부가 되지 않은 환경에서 얻은 미세 도플러 스펙트로그램을 학습하였으며, 테스트 데이터로는 잡음이 부가된 환경에서 얻은 미세 도플러 스펙트로그램을 사용하였다. 합성곱 신경망 구조는 기존에 잘 알려진 VGGNet(Visual Geometry Group Net)구조 중 11계층을 가지는 구조를 사용하였다. 그림 6은 제안하는 방법의 전처리 과정이며, 그림 7은 합성곱 신경망을 이용한 학습 과정 및 테스트 과정을 나타낸다.

Fig. 6.

Proposed pre-processing method

Fig. 7.

Training process and test process of CNN

Ⅴ. 시뮬레이션 결과

5.1 시뮬레이션 환경

기두부와 단 분리 시 조각의 미세 도플러 스펙트로그램을 획득하기 위해 먼저 동적 RCS를 계산해야 한다. 표적의 동적 RCS를 계산하기 위해 전자파 수치해석 툴인 FEKO를 이용하였다. 그러나 FEKO는 움직이는 표적의 RCS를 계산하는 것이 불가능하다. 따라서 본 논문에서는 3장에서 설명한 방법을 통해 안테나의 위치를 구하였으며, 이를 FEKO에 적용하여 동적 RCS를 계산하였다.

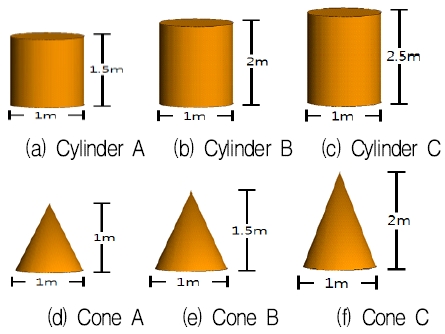
기두부는 총 4종류의 3-D CAD모델을 제작하였으며, 단 분리 시 조각은 원뿔 3종, 원기둥 3종의 3-D CAD모델을 제작하였다. 또한 기두부는 별도의 자세제어를 가지기 때문에 단 분리 시 조각보다 더 빠르게 회전하도록 가정하여 파라미터를 설정하였다. 그림 7과 그림 8을 탄두와 단 분리 시 조각의 3-D CAD 모델이며, 표 1은 탄두와 단 분리 시 조각의 미세 운동 파라미터 값이다.

Fig. 7.

3-D CAD models of the warhead

Fig. 8.

3-D CAD models of the debris

Table 1.

Nutation and tumbling motion parameters

주파수 대역은 3GHz 단일 주파수를 사용하였으며, 편파 각은 90°로 수평 선형 편파만을 고려하였다. PRF(Pulse Repetition Frequency)는 1kHz, 관측 시간은 0.25초이며, 고도각은 0°∼80°까지 10° 간격으로 표적의 동적 RCS 데이터베이스를 구축하였다. 구축한 동적 RCS 데이터베이스를 통해 미세 도플러 스펙트로그램을 획득하였으며, 획득한 미세 도플러 스펙트로그램에 CA-CFAR를 적용하였다. 미세 도플러 스펙트로그램에서 표적의 미세 도플러 주파수가 여러 픽셀에 거쳐 나오기 때문에 보호 셀의 범위를 넓게 잡았으며, 임계값을 결정하는 K₀값을 변화 시켜가며 합성곱 신경망의 입력 영상으로 사용하였다. 표 2는 CA-CFAR의 파라미터이다.

Table 2.

CA-CFAR parameters

전처리 과정을 수행하여 획득한 미세 도플러 스펙트로그램은 합성곱 신경망의 입력 영상으로 사용하였다. 학습 데이터로는 잡음이 부가 되지 않은 미세 도플러 스펙트로그램을 사용하였다. 영상의 수는 탄두 14,400개, 단 분리 시 조각 14,499개로 총 28,899개이며, 이중 90%는 학습 데이터로, 10%는 검증 데이터로 사용하였다. 또한 SGDM(Stochastic Gradient Descent with Momentum)을 통해 가중치를 수정하였으며, 학습률은 0.01, 미니 배치 크기(Mini-batch size)는 128, epoch는 5, 완전 연결 된 계층에 50% 확률의 드롭아웃을 적용하여 학습을 하였다. 이 때 계산 속도를 높이기 위해 1개의 GPU를 사용하였으며, 사용된 GPU는 GeForce GTX 750 Ti(2.15GHz)이다[19].

테스트 데이터로는 백색 가우시안 잡음이 부가된 환경에서 획득한 미세 도플러 스펙트로그램을 사용하여 기두부와 단 분리 시 조각의 구분 실험을 수행하였다. 또한 구분 결과의 신뢰성을 높이기 위해 50회의 몬테카를로 시뮬레이션을 수행하였다.

5.2 시뮬레이션 결과

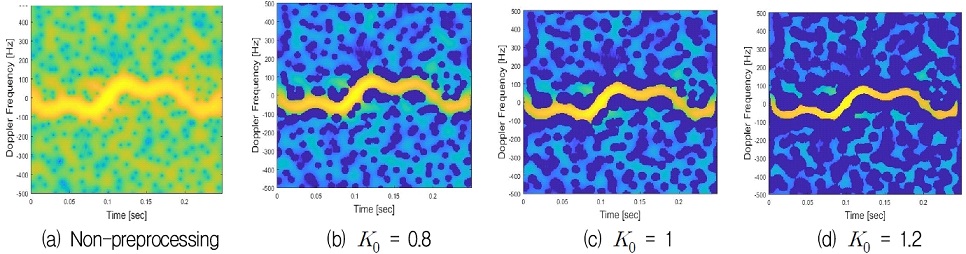
본 논문에서는 기두부와 단 분리 시 조각의 동적 RCS 데이터베이스를 통해 미세 도플러 스펙트로그램을 획득하였으며, 획득한 미세 도플러 스펙트로그램에 CA-CFAR를 적용하였다. CA-CFAR를 이용하여 전처리 과정을 수행하였을 경우, 미세 도플러 스펙트로그램에서 존재하는 잡음들이 일부 제거되는 것을 확인 할 수 있었다. 또한 값이 클수록 잡음이 더욱더 제거 되었지만 미세 도플러 주파수의 정보도 손실 되는 것을 확인하였다.

그림 9와 그림 10은 기두부와 단 분리 시 조각의 전처리 과정을 수행하지 않은 미세도플러 스펙트로그램과 K₀값에 따라 전처리 과정을 수행한 미세도플러 스펙트로그램이다. 그림에서 기두부의 경우 원추 운동 기울임 각은 6°, 진동 운동 기울임 각은 1°, 진동 운동 초당 회전 수는 62.83rad/s일 때의 미세 도플러 스펙트로그램을 나타내었으며, 단 분리 시 조각의 경우 텀블링 운동 초당 회전수가 18.84rad/s일 때의 미세 도플러 스펙트로그램을 나타내었다.

Fig. 9.

Micro-Doppler spectrogram of warhead (Target : A, Elevation angle : 0°, SNR : 10dB)

Fig. 10.

Micro-Doppler spectrogram of warhead (Target : Cone A, Elevation angle : 0°, SNR : 10dB)

이와 같이 전처리 과정을 수행하여 획득한 미세 도플러 스펙트로그램을 합성곱 신경망의 입력 영상으로 사용하여 기두부와 단 분리 시 조각을 구분 하였으며, 그 결과를 전처리 과정을 수행하지 않은 미세 도플러 스펙트로그램을 입력 영상으로 사용하였을 경우와 비교하였다. 또한 K₀값에 따른 기두부와 단 분리 시 조각의 구분 성능도 비교하였다.

시뮬레이션 결과, K₀값에 상관없이 모든 SNR환경에서 전처리를 수행하지 않은 미세 도플러 스펙트로그램보다 구분 성능이 최소 2.24%에서 최대 15.99%까지 향상 된 것을 확인하였다. 또한 K₀의 값이 1.2일 때, SNR이 0dB에서 83.39%로 잡음에 가장 강건함을 보여주었을 뿐만 아니라, SNR이 20dB에서도 97.24%로 가장 높은 구분 성능을 보여주었다. 그림 11은 기두부와 단 분리 시 조각의 구분 결과를 나타낸다.

Fig. 11.

Classification result of warhead and debris

Ⅵ. 결 론

본 논문에서는 합성곱 신경망을 이용하여 기두부와 단 분리 시 조각을 구분하였다. 합성곱 신경망의 입력 영상으로는 미세 도플러 스펙트로그램을 사용하였다. 또한 구분 성능을 향상시키기 위해 미세 도플러 스펙트로그램에 CA-CFAR를 적용하여 전처리 과정을 수행하였다. 전처리 과정을 수행하는 단계에서 임계값을 결정하는 K₀값을 변경시켜가며 전처리 과정을 수행하였다. 따라서 전처리 과정을 수행하지 않은 미세 도플러 스펙트로그램과 K₀값에 따라 획득한 미세 도플러 스펙트로그램을 합성곱 신경망의 입력 영상으로 사용하여 기두부와 단 분리 시 조각을 구분하였으며, 그 구분 결과를 비교하였다.

시뮬레이션 결과, K₀값에 따라 상관없이 전처리 과정을 수행하여 미세 도플러 스펙트로그램을 획득하였을 경우, 전처리 과정을 수행하지 않은 미세 도플러 스펙트로그램보다 모든 SNR환경에서 높은 구분 성능을 보였다. 또한 K₀값이 1.2인 경우 SNR이 0dB에선 83.39%, 20dB에선 97.24%로 잡음에도 가장 강건하였으며, 구분 성능 또한 가장 높은 구분 성능을 보였다.

Acknowledgments

본 연구는 국방과학연구소의 지원(계약번호:UD170019FD)을 받아 수행하였으며, 이에 감사드립니다.

References

• H. Gao, L. Xie, S. Wen, and Y. Kuang, "Micro-Doppler signature extraction from ballistic target with micro-motions", IEEE Transaction on Aerospace and Electronic Systems, 46(4), p1969-1982, Oct.), (2010. [https://doi.org/10.1109/taes.2010.5595607]
• V. C. Chen, F. Li, and S. S. Ho, "Micro-Doppler effect in radar: Phenomenon model and simulation study", IEEE Transaction on Aerospace and Electronic Systems, 42(1), p2-21, Jan.), (2006. [https://doi.org/10.1109/taes.2006.1603402]
• H. Sun, Z. Liu, and N. Xue, "Ballistic Missile Warhead Recognition based on micro-Doppler Frequency", Defence Science Journal, 58(6), p705-709, Nov.), (2008.
• A. R. Persico, C. V. Ilioudis, C. Clemente, and J. Soraghan, "Novel Approach for Ballistic Targets Classification from HRRP frame", 2017 Sensor Signal Processing for Defence Conference (SSPD), p1-5, Dec.), (2017. [https://doi.org/10.1109/sspd.2017.8233248]
• P. Lei, K. Li, and Y. Liu, "Feature extraction and target recognition of missile targets based on micro-motion", 2012 IEEE 11th International Conference on Signal Processing, p1914-1919, Oct.), (2012. [https://doi.org/10.1109/icosp.2012.6491954]
• Y. J. Choi, I. S. Choi, J. W. Shin, and M. S. Chung, "Classification of the Front Body of a Missile and Debris in Boosting Part Separation Phase Using Periodic and Statistical Properties of Dynamic RCS", Journal of KIEES, 29(7), p540-549, Jul.), (2018.
• A. R. Persico, C. Clemente, D. Gaglione, C. V. Ilioudis, J. Cao, L. Pallotta, A. D. Maio, I. Proudler, and J. J. Soraghan, "On Model, Algorithms, and Experiment for micro-Doppler-Based Recognition of Ballistic Targets", IEEE Transaction on Aerospace and Electronic Systems, 53(3), p1088-1108, Jun.), (2017. [https://doi.org/10.1109/taes.2017.2665258]
• A. Krizhevsky, I. Sutskever, and G. Hinton, "ImageNet Classification with Deep Convolutional Neural Networks", In Proceedings of Advances in Neural Information and Processing Systems 25, p1090-1098, Dec.), (2012.
• C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich, "Going Deeper with Convolutions", 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), p1-9, Jun.), (2015. [https://doi.org/10.1109/cvpr.2015.7298594]
• K. Simonyan, and A. Zisserman, "Very Deep Convolutional Networks For Large-Scale Image Recognition", In Proceedings of International Conference on Learning Representations, p1-14, (2015).
• O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg, and L. F. Fei, "ImageNet large scale visual recognition challenge", International Journal of Computer Vision, 115(3), p211-252, Dec.), (2015. [https://doi.org/10.1007/s11263-015-0816-y]
• R. Wang, J. Lie, Y. Duan, H. Cao, and Y. Zhao, "Study on the Combined Application of CFAR and Deep Learning in Ship Detection", Journal of the Indian Society of Remote Sensing, 46(9), p1413-1421, Sep.), (2018. [https://doi.org/10.1007/s12524-018-0787-x]
• S. S. Seol, I. S. Choi, J. W. Shin, and M. S. Chung, "Design of Convolutional Neural Network Structure for the Identification of Warhead and Debris in the Separation Phase", Journal of KIIT, 16(6), p81-89, Jun.), (2018. [https://doi.org/10.14801/jkiit.2018.16.6.81]
• M. I. Skolnik, Introduction to RADAR systems, 3rd edition, McGraw-Hill, (2001).
• https://www.mathworks.com/help/phased/examples/constant-false-alarm-rate-cfar-detection.html, . [accessed: Nov. 05, 2018]
• Y. LeCun, Y. Bengio, and G. Hinton, "Deep learning", Nature, 521(7553), p436-444, May), (2015.
• I. Y. Kang, "Stability and Accuracy Analysis for the Shape of Supersonic Spin-stabilized Projectile", Pusan National University Master’s Thesis, (2003).
• D. C. Kwon, B. Y. Kang, "CPU and GPU Performance Analysis for Convolution Neural Network", Journal of KIIT, 15(8), p11-18, Aug.), (2017. [https://doi.org/10.14801/jkiit.2017.15.8.11]