이행관계를 고려한 클래스 간 커플링 강도 측정 방법

Ⅰ. 서 론

최근 소프트웨어 시스템의 규모가 커지고 복잡해짐에 따라서 시스템 구조의 분석을 통한 품질 향상의 중요성이 급증하고 있다. 이러한 중요성에 대응하기 위해 아래와 같이 다양한 측도들이 연구되었다[1].

•　Metric 1 : WMC(Weighted Methods Per Class) 하나의 클래스에 포함되는 메서드의 개수이다.
•　Metric 2 : DIT(Depth of Inheritance Tree) 클래스가 상속을 갖는 경우 최대 깊이를 의미한다.
•　Metric 3 : NOC(Number of Children) 특정 클래스를 상속받는 하위 클래스의 개수를 나타낸다.
•　Metric 4 : CBO(Coupling Between Object) 하나의 클래스가 참조하고 있는 다른 클래스들의 개수이다.
•　Metric 5 : RFC(Response For a Class) 해당 클래스의 모든 메서드와 이것들이 호출하는 모든 메서드들의 집합을 의미 한다.
•　Metric 6 : LCOM(Lack of Cohesion in Methods) 메서드에서 응집도가 얼마나 부족한가를 측정하는 측도이다.

이러한 측도들은 측정 방법에 따라 크게 정적 측도와 동적 측도로 나눌 수 있다[2]-[5]. 동적 측도는 수행 환경에 따라 달라지며, 고비용을 요구하므로 주로 보완 목적으로 사용되므로 일반적으로 정적 측도가 중요하다. 시스템 구조 분석과 클러스터링 그리고 선택적 회귀 테스트와 같은 다양한 품질 향상 기법들에서 정적인 측도 중에서 커플링이 가장 중요한 측도이다.

대표적인 품질 향상 기법으로는 시스템 분해, 리팩토링과 선택적 회귀테스트가 있으며, 이는 커플링 측도와 밀접한 관계가 있다. 각 기법과 커플링 측도와의 연관성을 분석해 보면 다음과 같다.

소프트웨어의 구조적 설계는 전체 개발 단계에 효과가 파급되는 중요한 역할을 한다. 일반적으로 설계자는 자신의 주관적 경험을 기반으로 소프트웨어 구조를 분해하여 설계를 수행한다. 이것은 때로 잘 적용되기도 하지만, 프로젝트 진행 중 요구 변경에 따라 계획된 구조가 변경되어 문제가 발생되는 경우가 많다. 따라서 많은 소프트웨어 품질 향상 도구는 소프트웨어 구조적 분석을 자동화하여 설계자 및 개발자들에게 측도에 대한 정보를 제공하여 시스템의 구조를 개선할 수 있게 한다. 이 경우 주로 클러스터링 기술을 사용하게 되는데, 클러스터링은 각 모듈간의 관련성 즉 커플링을 기반으로 요소들을 그룹화 하는 기술이다. 클러스터링을 위해서는 커플링의 제공이 핵심적인 요소이다[6].

소프트웨어 리팩토링은 프로그램의 외부 행위를 변경하지 않으면서 프로그램의 내부 구조를 개선하는 과정이다. 리팩토링의 결과로 코드의 모듈화, 재사용성, 유지보수성 같은 품질을 개선하여 개발의 속도를 높이고 코드의 복잡도를 낮출 수 있다. 이처럼 리팩토링이 소프트웨어의 유지보수 측면에서 유용하기 때문에 소프트웨어의 개발에서 많이 사용하고 있다. 시스템 분해를 통해 서브시스템이 추출되면, 서브시스템의 외부 인터페이스를 정의하기 위해 일종의 API인 Façade 객체를 추출해야 한다[7].

회귀 테스트는 오류 발생으로 인한 수정을 완료한 이후 이미 수행된 테스트를 전체적으로 재 수행하는 방법으로 많은 시간과 비용을 필요로 하는 문제를 가지고 있다. 선택적 회귀테스트는 기존 테스트 케이스 중에 수정된 부분에 의해 영향을 받을 수 있는 테스트케이스들만을 선택하기 때문에 일반 회귀 테스트 보다 시간과 비용을 대폭 낮출 수 있다[8]. 선택적 회귀 테스트에서 문제의 핵심은 다시 테스트해야 하는 부분을 선택하는 전략이다. 그러므로 커플링 측도는 변경된 부분에 따라 어떤 시스템 내부의 요소들이 테스트 되어야 하는가를 선택하는 문제에서 본 연구는 매우 유용하다.

위의 3가지 품질개선 방법은 서로 밀접한 연관을 갖고 있다. 커플링을 사용하여 시스템 분해(System Decomposition)를 수행하여 바람직하게 구조를 확보 할 수 있다[9]-[11]. 시스템 분해의 결과를 사용하여 리팩토링(Refactoring)에 도움을 줄 수 있다[12][13]. 또한, 커플링을 사용하여 시스템 내부의 모듈들의 연관성을 파악하여 선택적 회귀 테스트에서 수정된 코드와 연관되는 부분만을 효율적으로 선택하게 하여 회귀 테스트에서 시간과 비용을 낮출 수 있다.

기존의 커플링 측도를 판단하는 방법에서 다음과 같은 두 가지 문제점들이 존재한다[14]. 첫 번째, 소스코드의 길이에 의한 측정으로는 정확한 커플링 강도를 측정할 수 없다. 즉, 기존의 MLOC(Method Line of Code)로는 클래스간의 강도를 비교할 수 없다. 두 번째로 지금까지의 커플링에 대한 척도는 두 개의 클래스간의 직접적인 커플링 척도만 연구하였고, 이행 관계를 고려하지 않았다. 이행 관계를 고려하지 않게 되면, 직접적 참조관계는 없지만 간접적으로 충분한 강도를 갖는 커플링을 찾아내지 못한다. 이 결과로, 위에서 설명한 응용분야들에 충분히 적용되기가 어렵다.

따라서 본 논문에서는 기존 연구를 바탕으로 클래스간의 결합도를 비교할 수 있는 방법으로 참조 개수를 통한 결합 강도에 대해 제안하고, 이를 활용하여 이행적 참조를 고려한 커플링 척도를 제안하고자 한다.

논문의 구성은 다음과 같다. 관련연구에서는 객체 지향적 커플링 척도에 대한 연구사례와 문제점에 대해 살펴본다. 3장에서는 이 연구에서 제안하는 커플링 척도의 정의와 예에 대하여 살펴본다. 마지막으로 4장에서는 결론을 맺고 향후 연구에 대해서 논의한다.

Ⅱ. 관련 연구

Ⅲ. 참조 회수와 이행관계를 고려한 클래스 간 커플링 측정

3.1 참조 회수를 이용한 클래스 간의 커플링 강도의 측정

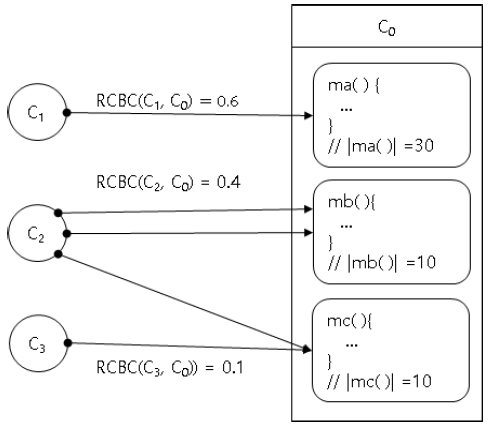
그림 1은 기존 연구에서 제안된 커플링 강도를 측정하는 RCBC에 대한 문제점을 반례로 보여준다. 그림에서 각 메서드의 하단 부분에 주석 내부에 기술된 숫자는 해당 매서드의 MLOC를 의미한다. 그림에서 C₁은 C₀.ma()를 한번 호출하고, MLOC({ma()})=30이고 MLOC(AR(C₀))=30+10+10=50이므로, RCBC(C₁, C₀)=30/50=0.6이 된다. C₂는 C₀.mb()를 두 번 호출하고 C₀.mc()를 한번 호출하게 된다. 이 경우 집합에서는 중복이 허용되지 않으므로 RCBC(C₂,C₀)=MLOC({mb(),mc()})/50=(10+10)/50=0.4가 된다. 동일한 방식으로 RCBC(C₃,C₀) =0.1이 된다. 이 경우 그림에서 “C₀과 가장 강한 커플링을 갖는 클래스는 C₁, C₂, C₃ 중 무엇인가?”라는 질문에 그림의 결과로 보면 C₁이 된다.

Fig. 1.

Coupling strength using MLOC

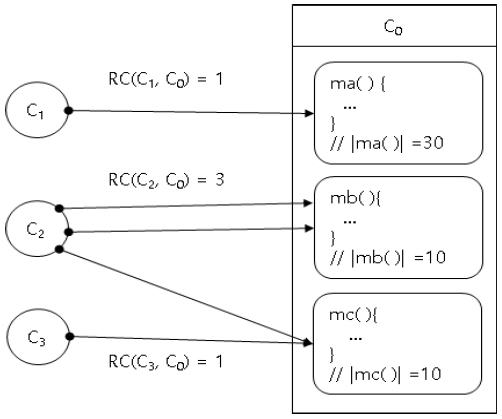
그림 2는 그림 1의 예를 본 연구에서 제안하는 커플링 강도를 적용한 것이다. 그림에서 화살표에 나타나는 RC(Reference Count)는 참조회수를 의미하며, 수식으로 정리하면 다음과 같다.

Fig. 2.

Coupling strength using RC

$\[ \text{RC}\left({\text{C}}_{\text{A}}\text{, }{\text{ C}}_{\text{B}}\right)\text{=}\left| \left\{\text{ line }\left|\text{ source line in }{\text{C}}_{\text{A}}\text{ that has references of }{\text{C}}_{\text{B}} \right.\right\} \right| \]$

(3)

식 (3)에서 | |는 집합의 원소의 개수를 의미한다. 이 경우 C₀과 가장 큰 결합도를 갖는 클래스는 C₂임을 알 수 있다. 결론적으로 그림 1에서는 RCBC를 기준으로 계산하면 C₁이 가장 높은 커플링을 갖지만, 그림 2에서와 같이 RC를 기준으로 하면 C₂와의 커플링이 가장 높다. 직관적으로 판단하면 참조 회수를 기준으로 계산하는 방법이 커플링을 더 정확하게 측정함을 알 수 있다. 특히 C₂는 mb() 메서드를 중복하여 호출하고 있다. RCBC를 기준으로 계산하는 경우에는 집합이 중복을 허용하지 않으므로 결합 강도에 고려되지 않지만 RC를 기준으로 하는 경우에는 중복 호출이 고려되어 보다 정확하게 계산된다.

보다 정확한 이해를 위해 그림 3의 프로그램 코드로 살펴보면 다음과 같다. EMP 클래스에 대해서 11개 라인의 소스코드가 작성되어 있고, 이 클래스는 ID 클래스와 DEPT 클래스를 참조하고 있다. RC(EMP, ID)는 2번째 라인에 1번의 참조가 있으므로 RC(EMP, ID) = | { 2 } | = 1이 된다. RC(EMP, DEPT)는 각각 라인 4, 6, 9에서 참조하고 있으므로, RC(EMP, DEPT) = | { 4, 6, 9 } | = 3이 된다.

Fig. 3.

Example source code

그림 2에서 나타나는 연결 강도를 상대적으로 측정하기 위해 먼저 ARC(All Reference Count)를 다음과 같이 정의하였다. 이것은 C_a를 참조하는 모든 클래스들에 대한 RC의 합을 의미한다.

$\[ ARC\left(C_a\right)=\sum _{i=1}^{n}RC\left(C_i,C_a\right) \]$

(4)

예를 들어 그림 2에서 ARC를 계산해 보면 다음과 같다. ARC(C₀)=1+3+1=5가 된다.

PCBC(Proportional Coupling Between Classes)는 하나의 클래스에 대해 이를 참조하는 클래스들과의 커플링 강도를 상대적으로 측정하기 위해 수식 (5)와 같이 정의하였다. PCBC(C₁,C₂)=C₂를 참조하고 있는 모든 클래스들의 RC에 대한 특정 클래스의 RC의 비율이다. 이 값은 0부터 1사이의 값을 가지게 되는데, 1에 가까울수록 결합도가 높으며, 0에 가까울수록 결합도가 낮다. 0의 의미는 결합도가 전혀 존재하지 않음을 나타낸다.

$\[ 0\le PCBC\left(C_1,C_2\right)=\frac{RC\left(C_1,C_2\right)}{ARC\left(C_2\right)}\le 1 \]$

(5)

그림 2의 사례에서 PCBC를 계산해 보면 ARC(C₀)=1+3+1=5이므로 PCBC(C₁,C₀)=1/5=0.2, PCBC(C₂,C₀)=3/5=0.6, PCBC(C₃,C₀)=1/5=0.2가 되어 보다 정확한 커플링 강도를 계산할 수 있어 기존 연구의 소스코드의 라인으로 계산하여 발생되는 문제를 해결할 수 있다. 예를 들어, 선택적 회귀테스트에 적용될 경우 PCBC를 사용하여, 재검사 대상 클래스들을 용이하게 선택할 수 있다. 클래스 C₁이 오류에 의해서 수정이 발생될 경우, 선택의 우선순위는 C₂, C₁, C₃ 또는 C₂, C₃, C₁이 된다.

3.2 이행관계를 고려한 클래스 간의 커플링 강도 측정

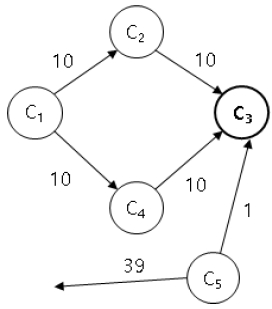
그림 4와 그림 5는 직접적인 참조관계 이외에 간접적인 참조관계도 매우 중요하다는 사실을 설명하고 있다. 그림 4에서 숫자는 각 클래스 간의 연결된 참조 회수를 의미하여 커플링 강도를 보여준다.

Fig. 4.

Example of the transitive coupling relationship

Fig. 5.

Conversion of the example in Fig. 4 to PCBC

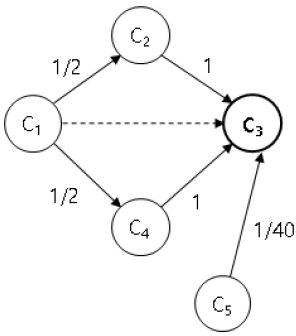
그림 5에서의 숫자는 한 클래스에서 다른 클래스들을 호출하는 확률을 보여준다. 예를 들어 선택적 회귀테스트에서 클래스 C₃을 수정하였을 경우 이를 참조하는 3개의 클래스를 선택하여 선택적 회귀 테스트를 수행하고자 한다고 가정해 보자. 이 경우 커플링 강도를 계산해보면 그림 4에서는 당연히 직접 연결된 클래스들 위주로 C₂, C₄, C₅가 선택된다.

그림 5는 C₃을 참조하는 모든 클래스들과의 PCBC를 계산하여 정리한 것이다. 그림 5에서 C₁과 C₃과의 커플링 강도를 이행적으로 고려해보면 1/2×1+1/2×1=1의 가장 강한 커플링 강도를 갖게 되어 C₁과 C₅의 대해 커플링 강도인 1/40보다 훨씬 크게 된다. 따라서 C₁, C₄, C₅가 선택되어야 한다. 따라서 이행성을 고려하면 보다 정확한 선택이 가능하다.

이 경우 C₁과 C₃사이에는 직접적 참조관계가 없기 때문에, PCBC를 계산할 수가 없다. 상식적으로 C₃이 변경되면 C₁도 영향을 받을 수밖에 없으므로 이행성을 고려한 척도가 필요하게 되어 tPCBC(Transitive Proportional Coupling Between Classes)를 다음 식 (6)과 같이 정의하였다.

$\[ tPCBC\left(C_a,C_b\right)=\sum _{i=1}^n\prod _{j=1}^{m}PCBC\left(C_j,C_{j+1}\right) \]$

(6)

이 수식에서 tPCBC는 두 개의 클래스 간에 이행적으로 도달할 수 있는 모든 경로에 대하여 인접하는 PCB를 곱한 것의 총 합을 의미한다. n은 C_a에서 C_b까지 도달 할 수 있는 모든 경로들의 개수이며, m은 해당경로의 위치한 클래스의 개수를 의미한다.

$\[ \begin{array}{c}tPCBC\left(C_1,C_3\right)=\sum _{i=1}^n\prod _{j=1}^{m}PCBC\left(C_1,C_3\right)\hfill \\ =\prod _{j=1}^{2}PCBC\left(C_j,C_{j+1}\right)+\prod _{j=1}^{2}PCBC\left(C_j,C_{j+1}\right)\hfill \\ \begin{array}{c}=PCBC\left(C_1,C_2\right)XPCBC\left(C_2,C_3\right)\hfill \\ \begin{array}{c}+PCBC\left(C_1,C_4\right)XPCBC\left(C_4,C_3\right)\hfill \\ =\frac{1}{2}X1+\frac{1}{2}X1=1\hfill \end{array}\hfill \end{array}\hfill \end{array} \]$

(7)

그림 5의 예에서 tPCBC(C₁, C₃)를 구하려면, 총 경로가 2개 즉 <C₁, C₂, C₃>와 <C₁, C₄, C₃>가 되어 수식 (7)과 같이 계산된다.

특정 클래스에서 다른 모든 클래스들 간의 연결강도를 구하는 알고리즘의 복잡도는 v가 정점의 개수이고 e가 간선의 개수인 경우 O(e + v∙log v)가 된다[16]. 시스템 분해이나 리팩토링을 위해서는 모든 클래스들 간의 커플링 강도의 계산이 필요하다. 수행시간을 분석하면 O(( e + v∙log v )∙v) = O(e∙v + v² ∙ log v)가 된다. 이를 분석해 보면 정점에 해당하는 클래스의 개수가 증가할수록 필요한 계산량이 급격하게 증가함을 알 수 있다. 작은 규모의 시스템이나 서브시스템으로 분해하여 분석하는 경우에는 사용 가능하지만, 시스템의 규모가 커질수록 기하급수적으로 증가하는 문제가 있다. 따라서 향후에는 우수한 성능을 갖는 모든 클래스들 간의 커플링 강도를 계산할 수 있는 방법의 연구가 필요하다.

Ⅳ. 결 론

커플링 강도를 측정하는 것은 시스템의 개발 및 유지보수에 있어서 매우 중요한 정보를 제공해 준다. 여러 가지 커플링 척도를 제공하는 연구가 진행되어져 왔지만, 기존의 연구 결과는 프로그램의 라인수를 기반으로 직접적 커플링 강도를 계산하는 것이었다.

본 연구에서는 이를 해결하기 위해 참조 횟수와 간접적인 연결을 고려한 커플링 강도를 측정하는 방법으로 RC, PCBC, 그리고 tPCBC를 제안하였다. 각 항목은 용도에 따라 부분적으로도 적용할 수 있다. RC의 경우에는 모든 클래스들 간의 연결 강도를 전역적으로 비교할 수 있다. 즉 서로 연관되지 않거나 연관성이 약한 두 개의 연결강도를 비교할 수 있다. 예를 들어 클래스 C_A와 C_B의 연결강도와 CX와 C_Y의 연결강도 중 어느 것이 더 강한가에 대한 질문에 대답할 수 있다. 따라서 시스템 분해와 같은 하향식 분석 기법에 적용할 수 있다. PCBC와 tPCBC의 경우에는 특정 클래스 C_A와 다른 클래스들 간의 연결강도를 클래스 C_A를 기준으로 상대적으로 비교하므로 전역적 비교가 불가능하지만 특정 클래스에 가장 큰 영향을 미치는 상향식 분석에 적용할 수 있다. 이를 사용하면 하나의 클래스에 대한 모든 클래스들의 상대적 연결강도를 비교할 수 있는 있어 선택적 회귀 테스트 분야에서 적용 가능하다.

향후 연구 과제로 제안된 척도를 이용하여 시스템 분해, 리팩토링과 선택적 회귀 테스트를 지원하기 방법과, 이와 같은 커플링 강도의 비교를 위해서는 상당한 연산을 요구하므로 성능 최적화에 대한 연구가 필요하다.

Acknowledgments

본 연구는 금오공과대학교 학술연구비에 의하여 연구된 논문임.

References

• L. C. Briand, J. Daly, and J. Wüst, "A Unified Framework for Coupling Measurement in Object Oriented Systems", IEEE Trans. on Software Eng., 25(1), p91-121, Jan/Feb.), (1999. [https://doi.org/10.1109/32.748920]
• S. R. Chidamber, and C. F. Kemerer, "A Metrics Suite for Object Oriented Design", IEEE Trans. Software Eng., 20(6), p476-493, Jun), (1994. [https://doi.org/10.1109/32.295895]
• E. Arisholm, L. C. Briand, and A. Føyen, "Dynamic Coupling Measurement for Object-Oriented Software", IEEE Trans. on Software Eng, 30(8), p491-506, Aug.), (2004. [https://doi.org/10.1109/tse.2004.41]
• S. Yacoub, H. Ammar, and T. Robinson, "Dynamic Metrics for Object-Oriented Designs", Proc. 6th Int’l Symp., Software Metrics, Boca Raton, FL, USA, p50-61, Nov.), (1999.
• E. Tempero, "Software Measurement The “CK” Metrics", COMPSCI702 (The University of Auckland) [Accessed: Mar. 10. 2019].
• Joung-Hee Park, Young-Mu Lee, and Jung-Keun Park, "RUAV Control Software Design and Verification using UML", The Journal of Korean Institute of Information Technology, 10(1), p27-35, Jan), (2012.
• C. Larman, "Applying UML and Patterns, 3rd Edition", Person Education Ltd, p13-579, (2007).
• Eui-Sub Kim, Dong-Ah Lee, and Junbeom Yoo, "RT-Selection: A Regression Test Selection Technique using Textual Differencing and Change Impact Analysis", Journal of KIISE, 41(6), p407-416, Jun.), (2014.
• C. H. Lung, M. Zaman, and A. Nandi, "Applications of Clustering Techniques to Software Partitioning, Recovery and Restructuring", The Journal of System and Software, 73(2), p227-224, Oct), (2004. [https://doi.org/10.1016/s0164-1212(03)00234-6]
• A. Alkhalid, C. H. Lung, and S. Ajila, "Software Architecture Decomposition using Adaptive K-Nearest Neighbor", Proceedings of IEEE Canadian Conference of Electrical And Computer Engineering(CCECE), Regina, SK, Canada, p1-4, May), (2013.
• Byeongdo Kang, Kicheol Jeon, Young-Kee Song, and Hyeong Ho Lee, "A Functional Decomposition Modeling for Switching Software", Proceedings of International Conference on Communication Technology. ICCT '96, p504-507, (2015).
• T. Mens, and T. Tourwe, "A Survey of Software Refactoring", IEEE Trans. on Software Eng., 30(2), p126-139, Feb.), (2004. [https://doi.org/10.1109/tse.2004.1265817]
• Kyung-Min Kim, and Tae-Gong Kim, "A Refactoring Composition Language for Composite Refactoring", Journal of KIISE, 39(7), p523-536, Jul.), (2012.
• Ji min Hwa, Suk hee Lee, and Yong Rae Kwon, "A Coupling Metric for Measuring Strength of Dependency between Classes in Object-Oriented Systems", Journal of KIISE, 14(1), p81-85, Jan.), (2008.
• Jun-Ha Lee, Uije Park, Yong B. Park, Soojin Park, and Sooyong Park, "Modularizing Software using Direct and Indirect Class Coupling Metrics", Journal of KISS: Software and Applications, 41(5), p327-339, May), (2014.
• M. L. Fredman, and R. E. Tarjan, "Fibonacci heaps and their uses in improved network optimization algorithms", 25th Annual Symposium on Foundations of Computer Science, IEEE, p338-346, Nov.), (1984. [https://doi.org/10.1109/sfcs.1984.715934]